Brealey, Myers. Principles of Corporate Finance. 7th edition

Подождите немного. Документ загружается.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

totally unrelated to other events in the economy. In this case the default risk is

wholly diversifiable, and the beta of the notes is zero. The notes would sell for

An investor who purchased these notes for $800 would receive a promised yield of

about 36 percent:

That is, an investor who purchased the notes for $800 would earn a 36.3 percent

rate of return if Backwoods does not default. Bond traders therefore might say that

the Backwoods notes “yield 36 percent.” But the smart investor would realize that

the notes’ expected yield is only 9 percent, the same as on risk-free bonds.

This of course assumes that risk of default with these notes is wholly diversifiable,

so that they have no market risk. In general, risky bonds do have market risk (that is,

positive betas) because default is more likely to occur in recessions when all busi-

nesses are doing poorly. Suppose that investors demand a 2 percent risk premium

and an 11 percent expected rate of return. Then the Backwoods notes will sell for

and offer a promised yield of , or

about 39 percent.

You rarely see traded bonds offering 39 percent yields, although we will soon en-

counter an example of one company’s bonds that had a promised yield of 50 percent.

Bond Ratings

The relative quality of most traded bonds can be judged from bond ratings given by

Moody’s and Standard and Poor’s. Table 24.4 summarizes these ratings. For example,

the highest quality bonds are rated triple-A (Aaa) by Moody’s, then come double-A

(Aa) bonds, and so on. Bonds rated Baa or above are known as investment-grade bonds.

Commercial banks, many pension funds, and other financial institutions are not al-

lowed to invest in bonds unless they are investment-grade.

11, 090/785.592⫺ 1 ⫽ .388872/1.11 ⫽ $785.59

Promised yield ⫽

$1, 090

$800

⫺ 1 ⫽ .363

PV of notes ⫽

$872

1.09

⫽ $800

684 PART VII

Debt Financing

Moody’s Ratings Standard and Poor’s Ratings

Investment-grade:

Aaa AAA

Aa AA

Baa BBB

Junk bonds:

Ba BB

Caa CCC

Ca CC

TABLE 24.4

Key to Moody’s and Standard and Poor’s bond

ratings. The highest quality bonds are rated triple-A.

Then come double-A bonds, and so on. Investment-

grade bonds have to be Baa or higher. Bonds that

don’t make this cut are called junk bonds.

Investment-grade bonds can usually be entered at face value on the books of banks and life insurance

companies.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

Bond ratings are judgments about firms’ financial and business prospects. There

is no fixed formula by which ratings are calculated. Nevertheless, investment

bankers, bond portfolio managers, and others who follow the bond market closely

can get a fairly good idea of how a bond will be rated by looking at a few key num-

bers such as the firm’s debt–equity ratio, the ratio of earnings to interest, and the

return on assets.

Table 24.5 shows that bond ratings do reflect the probability of default. Since

1971 no bond that was initially rated triple-A by Standard and Poor’s has defaulted

in the year after issue and fewer than one in a thousand has defaulted within 10

years of issue. At the other extreme, over 2 percent of CCC bonds have defaulted

in their first year and by year 10 almost half have done so. Of course, bonds rarely

fall suddenly from grace. As time passes and the company becomes progressively

more shaky, the agencies revise downward the bond’s rating to reflect the increas-

ing probability of default.

Since bond ratings reflect the probability of default, it is not surprising that there

is also a close correspondence between a bond’s rating and its promised yield. For

example, in the postwar period the promised yield on Moody’s Baa corporate

bonds has been on average about .9 percent more than on Aaa’s.

Firms and governments, having noticed the link between bond ratings and

yields, worry that a reduction in rating will result in higher interest charges.

When the Asian currency crisis in 1998 led Moody’s to downgrade the Malaysian

government’s risk rating, the government immediately canceled a much-needed

$2 billion bond issue. Investors have a different concern; they worry that the rating

agencies are slow to react when businesses are in trouble. When Enron went belly

up in 2001, investors protested that only two months earlier the company’s debt

had an investment-grade rating.

Junk Bonds

Bonds rated below Baa are known as junk bonds. Most junk bonds used to be fallen

angels, that is, bonds of companies that had fallen on hard times. But during the

1980s new issues of junk bonds multiplied tenfold as more and more companies is-

sued large quantities of low-grade debt to finance takeovers or to defend them-

selves against being taken over.

CHAPTER 24

Valuing Debt 685

Percentage Defaulting within

Rating at 1 Year 5 Years 10 Years

Time of Issue after Issue after Issue after Issue

AAA .0 .1 .1

AA .0 .7 .7

A.0.2.6

BBB .0 1.6 2.8

BB .4 8.3 16.4

B 1.5 22.0 33.0

CCC 2.3 35.4 47.5

TABLE 24.5

Default rates of corporate bonds

1971–1997 by Standard and Poor’s

rating at date of issue.

Source: R. A. Waldman, E. I. Altman, and

A. R. Ginsberg, “Defaults and Returns on

High Yield Bonds: Analysis through 1997,”

Salomon Smith Barney, New York, January

30, 1998.

They almost certainly exaggerate the influence of the rating agencies, which are as much following in-

vestor opinion as leading it.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

The development of this market for low-grade corporate bonds was largely the

brainchild of the investment banking firm Drexel Burnham Lambert. The result was

that for the first time corporate midgets were able to take control of corporate giants,

because they could finance this activity by issues of debt. However, issuers of junk

bonds often had debt ratios of 90 or 95 percent. Many worried that these high levels

of leverage resulted in undue risk and pressed for legislation to ban junk bonds.

One of the largest issuers of junk bonds was Campeau Corporation. Between

1986 and 1988 Campeau amassed a huge retailing empire by acquiring major de-

partment store chains such as Federated Department Stores and Allied Stores. Un-

fortunately, it also amassed $10.9 billion in debt, which was supported by just $.9

billion of book equity. So when in September 1989 Campeau announced that it was

having difficulties meeting the interest payments on its debt, the junk bond mar-

ket took a nosedive and worries about the riskiness of junk bonds intensified.

Campeau’s own bonds fell to the point at which they offered a promised yield of

nearly 50 percent. Campeau eventually filed for bankruptcy, and investors with

holdings of junk bonds took large losses.

In 1990 and 1991 the default rate for junk bonds climbed to over 10 percent and

the market for new issues of these bonds dried up. But later in the decade the mar-

ket began to boom again and with increasing economic prosperity the annual de-

fault rate fell to below 2 percent before rising again in the new millenium.

Junk bonds promise a higher yield than U.S. Treasuries. When junk bonds were

out of favor, their yields reached more than 9 percent above that of Treasuries, but

the gap has since narrowed. Of course, companies can’t always keep their prom-

ises. Many junk bonds have defaulted, while some of the more successful issuers

have called their bonds, thus depriving their holders of the prospect of a continu-

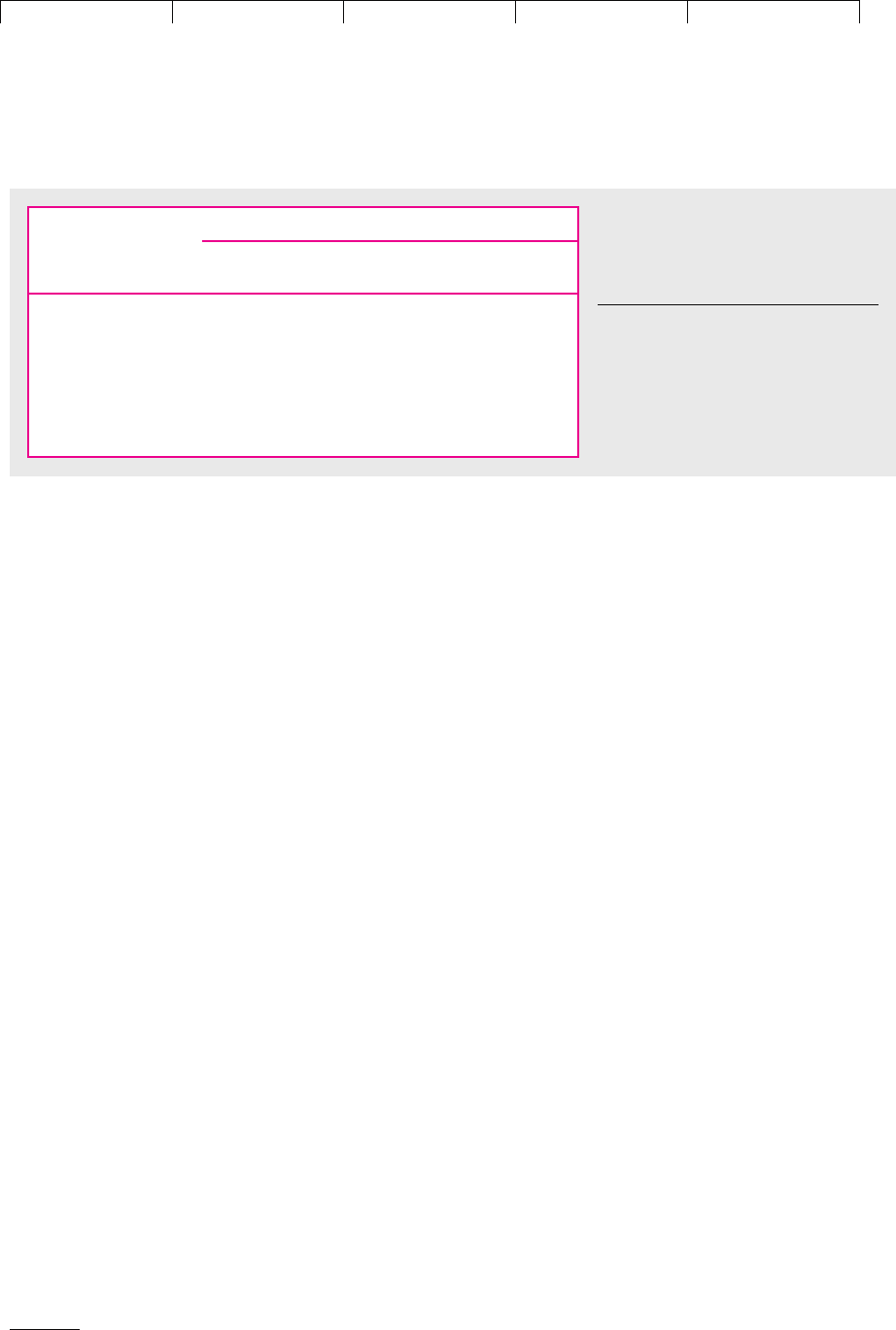
ing stream of high coupon payments. Figure 24.8 shows the performance since

1977 of a portfolio of junk bonds and 10-year Treasury bonds. On average, the

promised yield on junk bonds was 4.8 percent higher than that on Treasuries, but the

annual realized return was only 1.9 percent higher.

Option Pricing and Risky Debt

In Section 20.2 we showed that holding a corporate bond is equivalent to lending

money with no chance of default but at the same time giving stockholders a put

option on the firm’s assets. When a firm defaults, its stockholders are in effect ex-

686 PART VII

Debt Financing

1977

1979

1981

1983

1985

1987

1989

1991

1993

1995

1997

1999

Year

Cumulative value, dollars

U.S. Treasury bonds

Junk bonds

FIGURE 24.8

Cumulative value of investments in

junk and Treasury bonds,

1978–2000. The plot assumes

investment of $1 in 1977.

Source: E. I. Altman, “High Yield Bond

and Default Study,” Salomon Smith

Barney, July 19, 2001.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

ercising their put. The put’s value is the value of limited liability—the value of

stockholders’ right to walk away from their firm’s debts in exchange for handing

over the firm’s assets to its creditors. Thus, valuing bonds should be a two-step

process:

The first step is easy: Calculate the bond’s value assuming no default risk. (Dis-

count promised interest and principal payments at the rates offered by Treasury is-

sues.) Second, calculate the value of a put written on the firm’s assets, where the

maturity of the put equals the maturity of the bond and the exercise price of the

put equals the promised payments to bondholders.

Owning a corporate bond is also equivalent to owning the firm’s assets but giv-

ing a call option on these assets to the firm’s stockholders:

Thus you can also calculate a bond’s value, given the value of the firm’s assets, by

valuing a call option on these assets and subtracting the call value from the asset

value. (The call value is just the value of the firm’s common stock.) Therefore, if you

can value puts and calls on a firm’s assets, you can value its debt.

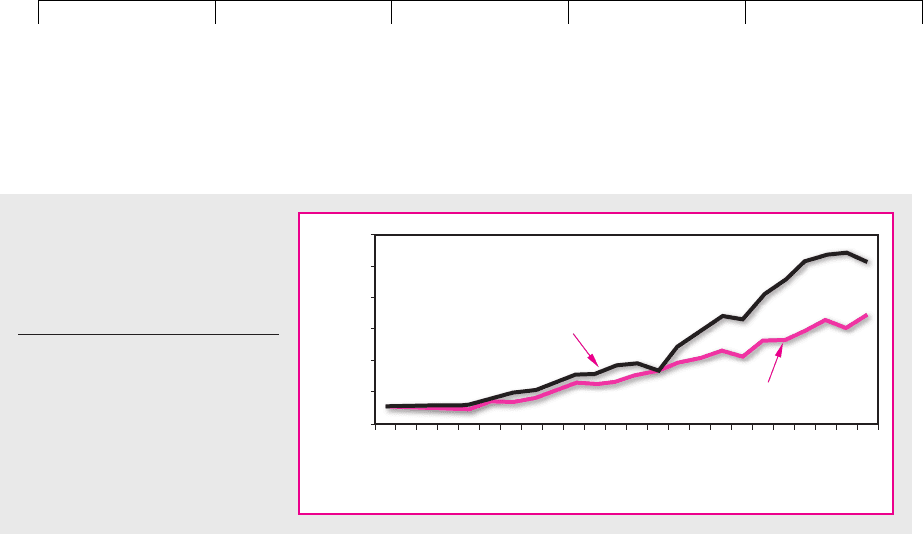
Figure 24.9 shows a simple application of option theory to pricing corporate

debt. It takes a company with average operating risk and shows how the promised

interest rate on its debt should vary with its leverage and the maturity of the debt.

For example, if the company has a 20 percent debt ratio and all its debt matures in

25 years, then it should pay about one-half percentage point above the government

borrowing rate to compensate for default risk. Companies with more leverage

ought to pay higher premiums. Notice that at relatively modest levels of leverage,

promised yields increase with maturity. This makes sense, for the longer you have

to wait for repayment, the greater is the chance that things will go wrong. How-

ever, if the company is already in distress and its assets are worth less than the face

value of the debt, then promised yields are higher at low maturities. (In our exam-

ple, they run off the top of the graph for maturities of less than four years.) This

also makes sense, for in these cases the longer that you wait, the greater is the

chance that the company will recover and avoid default.

Notice that in constructing Figure 24.9 we made several artificial assumptions.

One assumption is that the company does not pay dividends. If it does regularly

pay out part of its assets to stockholders, there may be substantially fewer assets to

protect the bondholder in the event of trouble. In this case, the market may be jus-

tified in requiring a higher yield on the company’s bonds.

There are other complications that make the valuation of corporate debt and eq-

uity a good bit more difficult than it sounds. For example, in constructing Figure 24.9

Bond value ⫽ asset value ⫺ value of call option on assets

bond value value

Bond value ⫽ assuming no chance ⫺ of put

of default option

CHAPTER 24 Valuing Debt 687

However, option-valuation procedures cannot value the assets of the firm. Puts and calls must be val-

ued as a proportion of asset value. For example, note that the Black–Scholes formula (Section 21.3) re-

quires stock price in order to compute the value of a call option.

Sarig and Warga plot the difference between corporate bond yields and the yield on U.S. Treasuries.

They confirm that the yield difference increases with maturity for high-grade bonds and declines for

low-grade bonds. See O. Sarig and A. Warga, “Bond Price Data and Bond Market Liquidity,” Journal of

Financial and Quantitative Analysis 44 (1989), pp. 1351–1360. Incidentally, the shape of the curves in Fig-

ure 24.9 depends on how leverage is defined. If we had plotted curves for constant ratios of the market

value of debt to debt plus equity, the curves would all have started at zero.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

we assumed that the company made only a single issue of zero-coupon debt. But

suppose instead that it issues a 10-year bond which pays interest annually. We can

still think of the company’s stock as a call option that can be exercised by making the

promised payments. But in this case there are 10 payments rather than just 1. To

value the stock, we would have to value 10 sequential call options. The first option

can be exercised by making the first interest payment when it comes due. By exer-

cise the stockholders obtain a second call option, which can be exercised by making

the second interest payment. The reward to exercising is that the stockholders get a

third call option, and so on. Finally, in year 10 the stockholders can exercise the tenth

option. By paying off both the principal and the last year’s interest, the stockholders

regain unencumbered ownership of the company’s assets.

Of course, if the firm does not make any of these payments when due, bond-

holders take over and stockholders are left with nothing. In other words, by not ex-

ercising one call option, stockholders give up all subsequent call options.

Valuing the equity when the 10-year bond is issued is equivalent to valuing the

first of the 10 call options. But you cannot value the first option without valuing

the nine that follow.

Even this example understates the practical difficulties, be-

cause large firms may have dozens of outstanding debt issues with different inter-

est rates and maturities, and before the current debt matures they may make fur-

ther issues. But do not lose heart. Computers can solve these problems, more or less

by brute force, even in the absence of simple, exact valuation formulas.

In practice, interest rate differentials tend to be greater than those shown in Fig-

ure 24.9. High-grade corporate bonds typically offer promised yields about 1 per-

centage point greater than U.S. Treasury bonds. It is very difficult to justify yield

688 PART VII

Debt Financing

5 7 9 11 13 15 17 19 21 23 25

Maturity,

years

Leverage = 120%

Leverage = 60%

Leverage = 40%

Leverage = 20%

Difference between

promised yield on bond

and risk-free rate, percent

FIGURE 24.9

How the interest rate on

risky corporate debt

changes with leverage and

maturity. These curves are

calculated using option

pricing theory under the

following simplifying

assumptions: (1) the risk-free

interest rate is constant for

all maturities; (2) the

standard deviation of the

returns on the company’s

assets is 25 percent per

annum; (3) debt is in the

form of zero-coupon bonds;

and (4) leverage is the ratio

, where E is the

market value of equity and

D is the face value of the

debt discounted at the risk-

free interest rate.

D/1 D ⫹ E2

The other approach to valuing the company’s debt (subtracting the value of a put option from risk-

free bond value) is no easier. The analyst would be confronted by not one simple put but a package of

10 sequential puts.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

differentials of this magnitude simply in terms of default risk.

So what is going

on here? One possibility is that companies are paying too much for their debt, but

it seems likely that the high yields on corporate bonds stem in part from some other

drawback. One possibility is that investors demand additional yield to compensate

for the illiquidity of corporate bonds. There is little doubt that investors prefer

bonds that are easily bought and sold. We can even see small yield differences in

the Treasury bond market, where the latest bonds to have been issued (known as

“on-the-run” bonds) are traded much more heavily and typically yield a few basis

points less than more seasoned issues.

Valuing Government Loan Guarantees

In the summer of 1971 Lockheed Corporation was in trouble. It was nearly out of

cash after absorbing heavy cost overruns on military contracts and, at the same

time, committing more than $800 million

to the development of the L1O11 Tri-

Star airliner. After months of suspense and controversy, the U.S. government res-

cued Lockheed by agreeing to guarantee up to $250 million of new bank loans. If

Lockheed had defaulted on these loans, the banks could have gotten their money

back directly from the government.

From the banks’ point of view, these loans were as safe as Treasury notes. Thus,

Lockheed was assured of being able to borrow up to $250 million at a favorable

rate.

This assurance in turn gave Lockheed’s banks the confidence to advance the

rest of the money the firm needed.

The loan guarantee was a helping hand—a subsidy—to bring Lockheed

through a difficult period. What was it worth? What did it cost the government?

This loan guarantee did not turn out to cost the government anything, because

Lockheed survived, recovered, and paid off the loans that the government had

guaranteed. Does that mean that the value of the guarantee to Lockheed was also

zero? Does it mean the government absorbed no risks when it gave the guarantee

in 1971, when Lockheed’s survival was still uncertain? Of course not. The govern-

ment absorbed the risk of default. Obviously the banks’ loans to Lockheed were

worth more with the guarantee than they would have been without it.

The present value of a loan guarantee is the amount lenders would be willing to

pay to relieve themselves of all risk of default on an otherwise equivalent unguar-

anteed loan. It is the difference between the present value of the loan with the guar-

antee and its present value without the guarantee. A guarantee can clearly have

substantial value on a large loan when the chance of default by the firm is high.

It turns out that a loan guarantee can be valued as a put on the firm’s assets,

where the put’s maturity equals the loan’s maturity and its exercise price equals

the interest and principal payments promised to lenders. We can easily show the

equivalence by starting with the definition of the value of the guarantee.

Value of

⫽

value of

⫺

loan value without the

guarantee guaranteed loan guarantee

CHAPTER 24

Valuing Debt 689

See, for example, J. Huang and M. Huang, “How Much of the Corporate-Treasury Yield is Due to

Credit Risk? Results from a New Calibration Approach,” working paper, Pennsylvania State Univer-

sity, August 2000.

See U. Reinhardt, “Break-Even Analysis for Lockheed’s TriStar: An Application of Financial Theory,”

Journal of Finance 28 (September 1973), pp. 821–838.

Lockheed paid the current Treasury bill rate plus a fee of roughly 2 percent to the government.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

Without a guarantee, the loan becomes an ordinary debt obligation of the firm. We

know from Section 20.2 that

The loan’s value, assuming no chance of default, is exactly its guaranteed value;

thus, the put value equals the difference between the values of a guaranteed and

an ordinary loan. This is the value of the loan guarantee.

Thus, option pricing theory should lead to a way of calculating the actual cost

of the government’s many loan guarantee programs. This will be a healthy thing.

The government’s possible liability under existing guarantee programs has been

enormous. In 1987, for example, $4 billion in loans to shipowners had been guar-

anteed under the so-called Title IX program to support shipyards in the United

States.

This program was one of dozens. Yet the true cost of these programs is

not widely recognized. Because loan guarantees involve no immediate outlay,

they do not appear in the federal budget. Members of Congress sponsoring loan

guarantee programs do not, as far as we know, present careful estimates of the

value of the programs to business and the present value of the programs’ cost to

the public.

Calculating the Probability of Default

Banks and other financial institutions not only want to know the value of the

loans that they have made but they also need to know the risk that they are in-

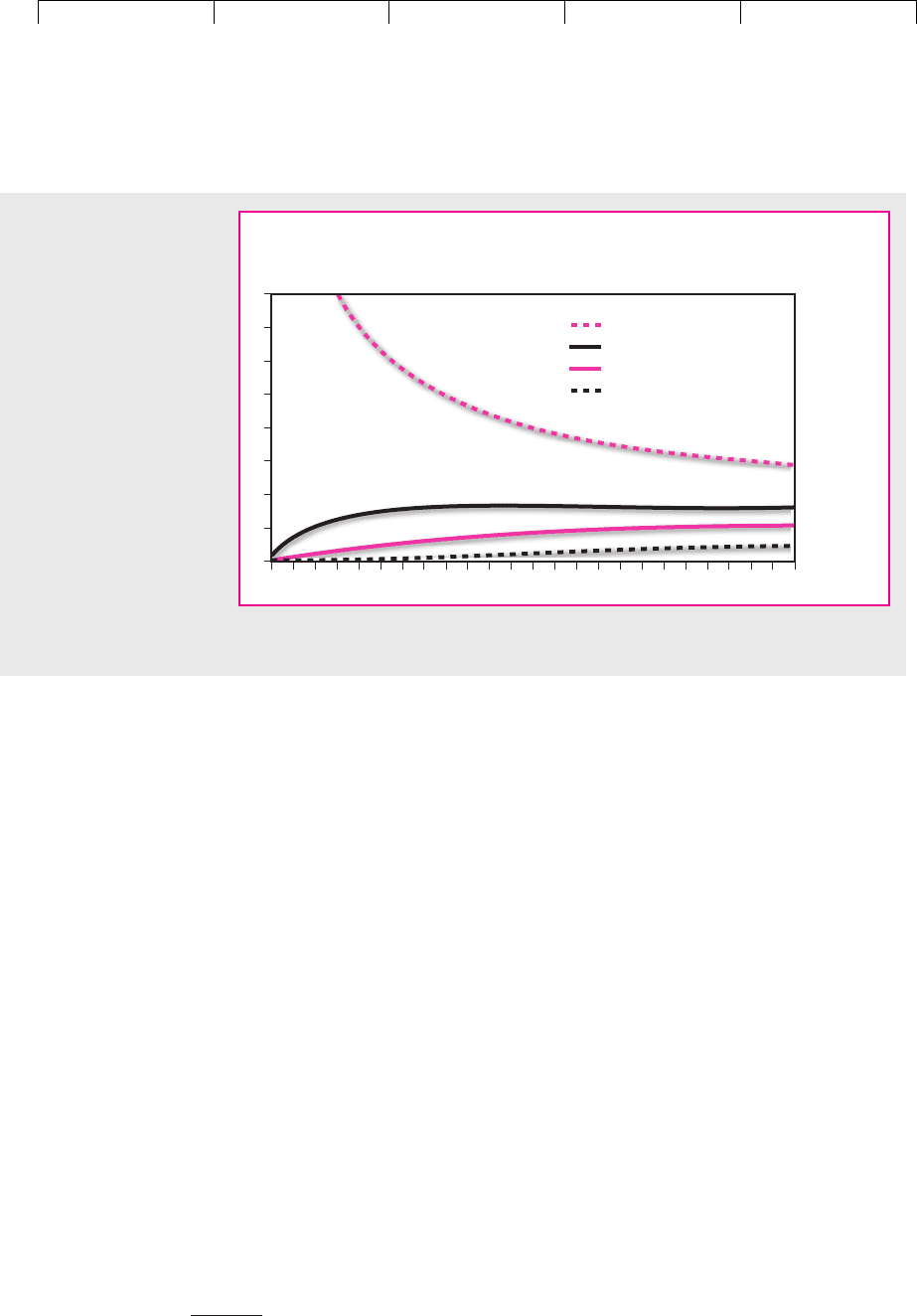
curring. Suppose that the assets of Backwoods Chemical have a current market

value of $100 and its debt has a face value of $60 (i.e., 60 percent leverage), all of

which is due to be repaid at the end of five years. Figure 24.10 shows the range

Value of value assuming

ordinary ⫽ no chance of ⫺ value of put option

loan default

690 PART VII

Debt Financing

The actual figure on March 31, 1987, was $4,497,365,297.98. Since 1987 these government guarantees

to shipowners have been substantially reduced.

Default

point

= $60

Expected

value

= $120

Value of assets

Probability

FIGURE 24.10

Backwoods Chemical

has issued five-year

debt with a face value

of $60. The shaded

area shows that there

is a 20 percent proba-

bility that the value of

the company’s assets

in year 5 will be less

than $60, in which

case the company will

choose to default.

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

of possible values of Backwoods’s assets when the loan becomes due. The ex-

pected value of the assets is $120, but this value is by no means certain. There is

a probability of 20 percent that the asset value could fall below $60, in which case

the company will default on its debt. This probability is shown by the shaded

area in Figure 24.10.

To calculate the probability that Backwoods will default, we need to know the

expected growth in the market value of its assets, the face value and maturity of

the debt, and the variability of future asset values. Real-world cases are likely to be

more complex than our Backwoods example. For example, firms may have several

classes of debt maturing on different dates. If so, shareholders have an option on

an option. It may be worth their while to put up more money to pay off the short-

term debt and thus keep alive the chance that the firm’s fortunes will recover be-

fore the rest of the debt becomes due.

However, banks and consulting firms are now finding that they can use

these ideas to measure the risk of actual loans.

For example, by mid-2001 the

fiber-optics company, Metromedia Fiber Network, was a company in difficul-

ties. Revenues had expanded rapidly, but so had losses. By 2000 the company

was making operating losses of $329 million on revenues of $188 million. The

stock price had fallen from a high of $50 to under $2, while the company’s

8-year 10 percent notes were priced at 44 percent and offered a yield to matu-

rity of 27 percent.

How close was Metromedia to default? Figure 24.11 provides an answer. The

burgundy line shows the market value of Metromedia’s assets, and the blue line

shows the asset value at which the company would choose to default on its debts.

You can see that during the first half of 2001 the value of the company’s assets crept

closer and closer to the default point.

CHAPTER 24

Valuing Debt 691

Banks are not just interested in the risk of individual loans; they would also like to know the risk of

their entire portfolio. Therefore, specialists in credit risk also need to recognize the correlation between

the outcomes. A portfolio of loans, all of which are to factory outlets in suburban Hicksville, is likely to

be more risky than a portfolio with a wide variety of different borrowers.

1000

2000

3000

4000

5000

6000

7000

8000

9000

10000

Value, $ millions

Market value of assets

Default point

22/02/01

08/03/01

22/03/01

05/04/01

19/04/01

03/05/01

17/05/01

31/05/01

14/06/01

28/06/01

FIGURE 24.11

The market value of the

assets of Metromedia Fiber

Network crept closer to the

point at which the firm would

choose to default.

Source: KMV Credit Monitor.

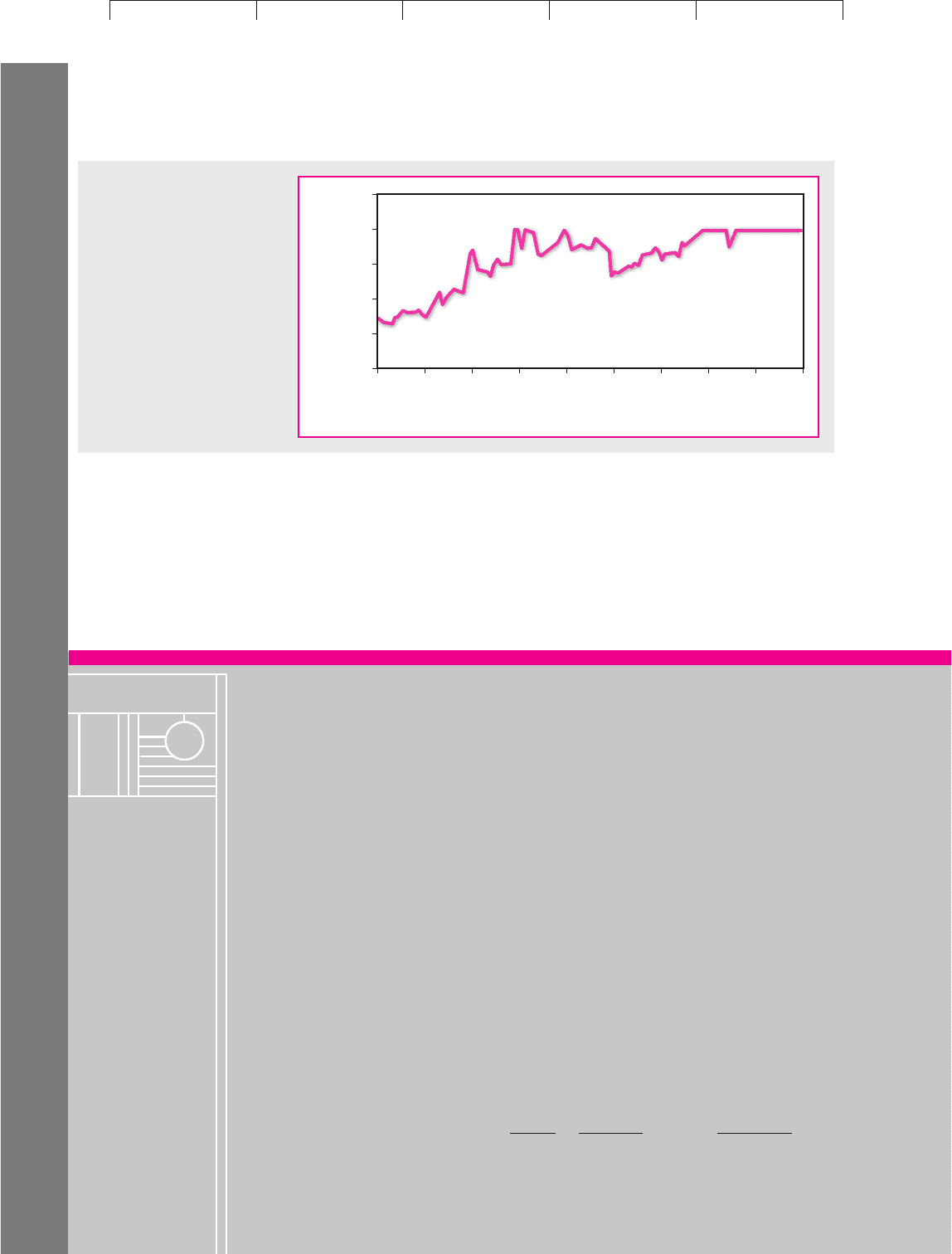
Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

692 PART VII Debt Financing

Of course, nobody had a crystal ball that could foresee what would happen to

Metromedia, but KMV, a consulting firm specializing in the assessment of credit

risk, estimated the probability at each point that the company would default in the

next year. Figure 24.12 shows how KMV progressively increased its assessment of

the probability of default.

Probability of default over

next year, percent

22/02/01

08/03/01

22/03/01

05/04/01

19/04/01

03/05/01

17/05/01

31/05/01

14/06/01

28/06/01

FIGURE 24.12

Estimates by KMV Credit

Monitor of the probability that

Metromedia Fiber Network

would default on its debt

within a year.

SUMMARY

Visit us at www.mhhe.com/bm7e

Efficient debt management presupposes that you understand how bonds are val-

ued. That means you need to consider three problems:

1. What determines the general level of interest rates?

2. What determines the difference between long-term and short-term rates?

3. What determines the difference between the interest rates on company and gov-

ernment debt?

Here are some things to remember. The rate of interest depends on the demand

for savings and the supply. The demand comes from firms who wish to invest in

new plant and equipment. The supply of savings comes from individuals who are

willing to consume tomorrow rather than today. The equilibrium interest rate is the

rate that produces a balance between the demand and supply.

The best-known theory about the effect of inflation on interest rates was sug-

gested by Irving Fisher. He argued that the nominal, or money, rate of interest is

equal to the expected real rate plus the expected inflation rate. If the expected in-

flation rate increases by 1 percent, so too will the money rate of interest. During the

past 50 years Fisher’s simple theory has not done a bad job of explaining changes

in short-term interest rates in the United States.

The value of any bond is equal to the cash payments discounted at the spot

rates of interest. For example, the value of a 10-year bond with a 5 percent

coupon equals

PV1percent of face value2⫽

1 ⫹ r

⫹

11 ⫹ r

⫹

…

⫹

105

11 ⫹ r

Brealey−Meyers:

Principles of Corporate

Finance, Seventh Edition

VII. Debt Financing 24. Valuing Debt

Companies, 2003

CHAPTER 24 Valuing Debt 693

Bond dealers generally look at the yield to maturity on a bond. This is simply

the internal rate of return y, the discount rate at which

The yield to maturity y is a complex average of the spot interest rates r

, r

, etc.

Like most averages it can be a useful summary measure, but it can also hide a lot

of interesting information. We suggest you refer to yields on stripped bonds as

measures of the spot rates of interest.

When you invest in a bond you usually receive a regular interest payment and

then the final principal payment. Duration measures the average time to each pay-

ment. It is a useful summary measure of the length of a loan. It is also important

because there is a direct relationship between the duration of a bond and its volatil-

ity. A change in interest rates has a greater effect on the price of a bond with a longer

duration.

The one-period spot rate may be very different from the two-period spot rate

. In other words, investors often want a different annual rate of interest for lend-

ing for one year than for two years. Why is this? The expectations theory says that

bonds are priced so that the expected rate of return from investing in bonds over

any period is independent of the maturity of the bonds held by the investor. The

expectations theory predicts that will exceed only if next year’s one-period in-

terest rate is expected to rise.

The expectations theory cannot be a complete explanation of the term structure

if investors are worried about risk. Long bonds may be a safe haven for investors

with long-term fixed liabilities. But other investors may not like the extra volatility

of long-term bonds and may be concerned that a sudden burst in inflation could

largely wipe out the real value of these bonds. Such investors will be prepared to

hold long-term bonds only if they offer a liquidity premium—that is, a higher rate

of interest.

Finally, we come to our third question: What determines the difference between

interest rates on company and government debt? Company debt sells at a lower

price than government debt. This discount represents the value of the company’s

option to default. We showed you how the value of this option varies with the de-

gree of leverage and the time to maturity.

Ratings are widely used as a guide to the risk of loans. However, banks and con-

sulting firms also recognize that the option to default is a put option and they have

been developing models to estimate the probability that the borrower will exercise

its option to default.

Bond price ⫽

1 ⫹ y

⫹

11 ⫹ y2

⫹

…

⫹

105

11 ⫹ y2

FURTHER

READING

A good general text on debt markets is:

A. Sundaresan and S. Sundaresan: Fixed Income Markets and Their Derivatives, South-Western

College Publishing, Cincinnati, Ohio, 2nd ed., 2001.

Nelson provides a useful review of some of the standard theories of the term structure literature:

C. R. Nelson: “The Term Structure of Interest Rates: Theories and Evidence,” in J. L. Bick-

sler (ed.), Handbook of Financial Economics, North-Holland Publishing Company, Ams-

terdam, 1980.

Visit us at www.mhhe.com/bm7e