Braibant S., Giacomelli G., Spurio M. Particles and Fundamental Interactions: An Introduction to Particle Physics
Подождите немного. Документ загружается.


320 11 The Standard Model of the Microcosm
11.3.2.2 Gauge Invariance in SU(2)
Following the QED example, more complicated groups were proposed; these groups
are specified by noncommutative operators in order to introduce other interactions
from a local invariance principle. For the isotopic spin initially associated with
the strong interaction, the SU(2) group was proposed. The conservation of weak
isotopic spin implies invariance under rotation in the isospin space
j
!
0
j
D e
i"
a
a
2
j
'
j
C i"
a
a
2
j
.a D 1; 2; 3/ (11.17)
where the index j represents each type of lepton, "
a
are infinitesimal arbitrary
parameters and
a
are the noncommutative Pauli matrices (Appendix 4) obeying
h
a
2
;
b
2
i
D i"
abc
c
2
(11.18)
where "
abc
is the totally antisymmetric tensor and .x/ are SU(2) isospinors. Let
us now require that "
a
be different in each space-time point, that is, "
a
D "
a
.x/.
Proceeding as for QED, a gauge invariant description is obtained by introducing
a massless isovector field A
with charged and neutral components and with a
coupling constant g similar to e. The invariance of the
D
terms under
the transformation (11.17) implies the introduction of the following covariant
derivative:
@
!r
@
C igA
a
a
2
: (11.19)
The vector nature of these fields leads to the gauge transformation
A
a
! A
a
1
g
@
"
a
.x/ "
abc
"
b
.x/A
c
: (11.20)
The additional term, with respect to (11.15), is associated with the fact that the
matrices do not commute. This also implies that there exists an interaction between
A
and all particles with isospin, including the A
themselves. In this way, A
are
both sources and carriers of the isospin field. Notice that the hypothetical charged
intermediate bosons of the isospin field are massless, just like the photon for the
electromagnetic field.
11.3.2.3 Gauge Invariance in SU(3)
A generalization is obtained by requiring that the Lagrangian density be invariant
under SU(N) rotations; in this case, one must have L.
0
/ D L. /,
0
D U ,
where U is an unitary matrix .U
C
U D 1/ that can be written as
11.3 Gauge Theories 321
RGB
RGB
RGB
GBR
RBB
RBG
a
b
c
global
rotation
local
rotation
local rot.
+ gluon
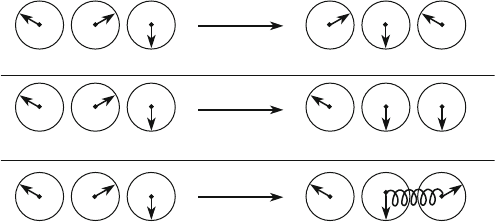
Fig. 11.2 Qualitative illustration of the difference between global and local rotations in the “color
space.” The initial state on the left is a colorless baryon made of three quarks of different colors.
(a) A global rotation changes the color of all three quarks at the same time, leaving the initial
baryon colorless. (b) Local rotations, different for each quark, can locally change the color, thus
changing the color of the initial baryon unless (c) the color is restored by the exchange of a gluon
U D exp
0
@
i
N
2
1
X
KD1
˛
K
F
K
1
A
(11.21)
where ˛
K
are the rotation parameters, F
K
are the rotation matrices and .N
2
1/
is the number of degrees of freedom. For SU(2), F
K
are the three .2 2/ Pauli
matrices; for SU(3), F
K
are the eight .3 3/
a
Gell–Mann matrices. The local
gauge invariance is then introduced by replacing the derivative @
with the covariant
derivative D
(D @
C ieB
, in QED), with the following property:
D
0
0
D UD : (11.22)
The covariant derivative transforms the material field , unlike the usual derivative
that transforms differently. We now require invariance under local (rather than
global) transformations (rotations). The interactions should therefore be invariant
under rotations of the symmetry group for each particle separately. The request
of local gauge invariance leads to the introduction of intermediate vector bosons
whose quantum numbers determine the interactions between the material fields,
as shown first by Yang and Mills in 1957 for the isospin symmetry of the strong
interaction. In the QCD framework, it is assumed that the interaction between two
quarks is mediated by the exchange of massless gluons with spin 1. It is also
assume that the interaction between two quarks is invariant under the exchange of
color. This implies that the three quarks of different colors are described by the
symmetry group SU(3)
C
,whereC stands for color. The quark SU(3)
C
symmetry is
considered exact. Figure 11.2 qualitatively shows the difference between global and
local rotations in the “color space” for a colorless baryon consisting of three quarks
322 11 The Standard Model of the Microcosm
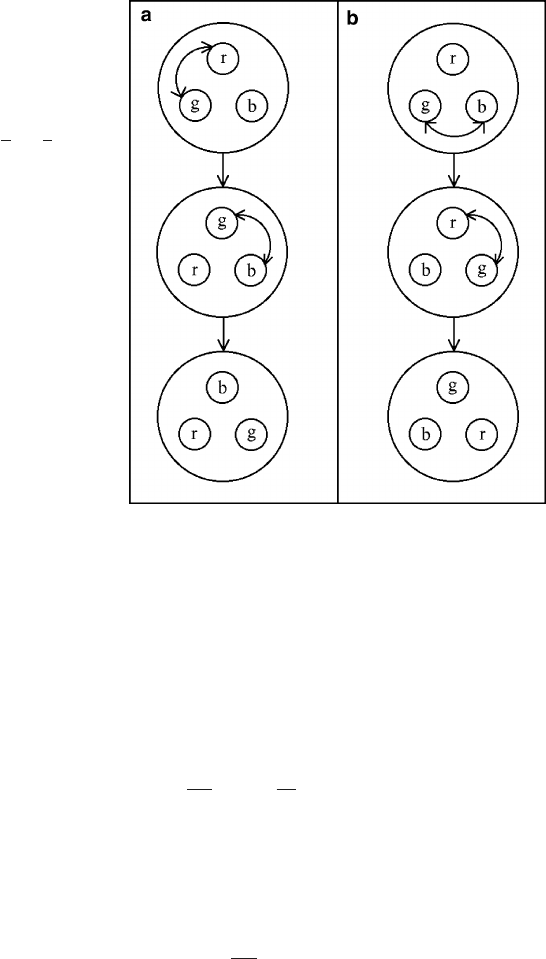
Fig. 11.3 Illustration of the
non-abelian nature of SU(3)
for a colorless baryon.
Starting from the same
hadron, (a) the quarks r and
g are swapped first,
exchanging a red-green gluon
(more precisely r
g or gr); the
quarks g and b are then
swapped (exchanging a
green-blue gluon). In (b)the
order of the color swaps is
inverted. The final results
shown at the bottom are not
the same; thus, these color
swaps do not commute
(non-abelian means that
A B ¤ B A)
of different colors. The color charges of gluons involve the non-abelian nature of
SU(3): rotations in the “color space” do not commute, as shown in Fig. 11.3.
11.4 Gauge Invariance in the Electroweak Interaction
The covariant derivative of the Standard Model in the electroweak interaction can
be written as
r
D @
C
ig
0
2
B
1 C
ig
2
A
a
a
(11.23)
where B
is the massless mediator of the field of the U(1) group, with coupling
constant g
0
. A
a
are the three massless quanta of SU(2) with coupling constant g.
This covariant derivative can be extended to include the strong interaction; in this
case, the covariant derivative can be written as
D
Dr
C
ig
s
2
G
a
a
(11.24)
where G
a
are the eight massless SU(3) quanta with coupling constant g
s
.The
treatment of the strong interaction will not be included here.
11.4 Gauge Invariance in the Electroweak Interaction 323
In (11.23), the term A
a
a
can be explicitly written as
A
1
1
C A
2
2
C A
3
3
D A
1
01
10
C A
2
0 i
i0
C A
3
10
0 1
D
A
3
A
1
iA
2
A
1
C iA
2
A
3
!
D
A
3
p
2W
C
p
2W
A
3
!
(11.25)
where
W
D
1
p
2
.A
1
C iA
2
/ (11.26)
W
C
D
1
p
2
.A
1
iA
2
/: (11.27)
Thus, the term
i
2
.g
0
B
1 C gA
a
a
/ in (11.23) explicitly becomes
i
2
g
0
B
C gA
3
p
2gW
C
p
2gW
g
0
B
gA
3
!
: (11.28)
The elements along the diagonal correspond to operators for transitions in which
the fermion electric charge is not changed (neutral currents). The nondiagonal W
C
,
W
elements act as “raising” and “lowering” operators in the weak isospin space
and transform, for example, an electron in its neutrino (or vice versa). The real
fields , Z
0
and W
˙
are obtained from the gauge fields after spontaneous symmetry
breaking (see Sect. 11.4.1).
11.4.1 Lagrangian Density of the Electroweak Theory
The procedure to construct a gauge invariant theory can be generalized to any
symmetry group and particularly to the SU(2) U(1) group in order to describe
electromagnetic and weak interactions in a unified model. The Dirac Lagrangian
density L for a free fermion is
L D i
@
m D .x/.i
@
m/ .x/: (11.29)
The first term represents the kinetic energy of the matter field with a mass m;the
second term, bilinear in , is the mass energy, proportional to the fermion mass m.
For a massive Higgs, the Lagrangian density is given by the Klein–Gordon equation:
L D .@
'
C
/.@
'/ m
2
'
C
': (11.30)

324 11 The Standard Model of the Microcosm
In this case, the term bilinear in ' is proportional to m
2
, the Higgs mass squared. The
Lagrangian density (11.29) must be invariant under SU(N) rotations, and therefore
L.
0
/ D L. /,
0
D U ,whereU is a unitary matrix .U
C
U D 1/.The
invariance under rotations can be verified for the mass term
m
0
0
D m U
C
U D m ; (11.31)
given that U
C
U D 1. The kinetic term of (11.29) is invariant under global
transformations (rotations), for which U is independent of x and can thus be treated
as a constant, namely,
L
0
kin
D U
C
@
U D U
C
U
@
D
@
D L
kin
: (11.32)
The local gauge invariance is introduced by replacing the derivative @
with the
covariant derivative of the [SU(2)
L
U(1)
Y
] group r
D @
C
ig
0
2
B
1 C
ig
2
A
a
a
.
The Lagrangian density (11.29)
L D i
r
m (11.33)
now transforms by
L
0
.
0
/ D i U
C
U r m U
C
U D i
r m D L. /: (11.34)
The new Lagrangian density describes the interaction between particles of matter
through the exchange of gauge bosons associated with the gauge fields, with the
coupling constants g and g
0
. The resulting Lagrangian density L. ; r
/ must
be completed by adding the Yang–Mills Lagrangian density, L
YM
, describing the
propagation of gauge fields:
L
YM
D
1
4
F
a
.F
a
/
1
4
G
G
(11.35)
where
F
a
D @
A
a
@
A
a
g"
abc
A
b
A
c
(11.36)
G
D @
B
@
B
: (11.37)
With a complete development of the Lagrangian density, it can be observed that
it does not contain quadratic terms for the gauge fields, for example, m
2
B
B
or
m
2
A
a
.A
a
/
, see also (11.30). Therefore, the gauge bosons associated with these
gauge fields are massless. The real fields , Z
0
and W
˙
are obtained from the
gauge fields after spontaneous symmetry breaking.

11.5 Spontaneous Symmetry Breaking. The Higgs Mechanism 325
11.5 Spontaneous Symmetry Breaking. The Higgs Mechanism
The gauge theory of the electroweak interaction described above involves fields
with massless propagators; but the vector boson mediators of the weak interaction,
W
˙
and Z
0
, have a nonzero mass; their masses are actually large. Higgs proposed
a mechanism that allows the mediators of the weak interaction to become massive
while the mediator of the electromagnetic interaction (the photon) remains massless.
This mechanism is the spontaneous symmetry breaking which keeps the Lagrangian
density still invariant under the group of gauge transformations [SU(2)
L
U(1)
Y
].
This mechanism requires the introduction of a new scalar boson, the so-called Higgs
boson and the corresponding Higgs field, whose self-interaction modifies the ground
state (the state with minimum energy) so that it is no longer a hypercharge or a weak
isospin eigenstate. The mass of the Higgs boson is not predicted by the theory. The
masses of the intermediate weak bosons and fermions are dynamically generated
through their interaction with the Higgs scalar field which is supposed to be present
everywhere in the space-time where the interaction occurs.
The Higgs mechanism considers a gauge invariant Lagrangian density L
H
,
corresponding to a self-interacting scalar isodoublet '. This Lagrangian density is
made of three terms and can be written in a symbolic way as
L
H
D L
r
L
V
C L
YM
(11.38a)
where
L
r
D .r
'/
C
.r
'/ (11.38b)
L
V
D V.'
C
'/ (11.38c)
L
YM
D
1
4
F
a
.F
a
/
1
4
G
G
: (11.38d)
The theory of superconductivity was taken as a model for this essential part of the
Standard Model of the microcosm. The Ginzburg–Landau potential in the theory of
superconductivity is used for the Higgs potential, L
V
D V.'
C
'/:
V.'
C
'/ D
2
'
C
' C .'
C
'/
2
(11.39)
where
2
and are complex constants. For
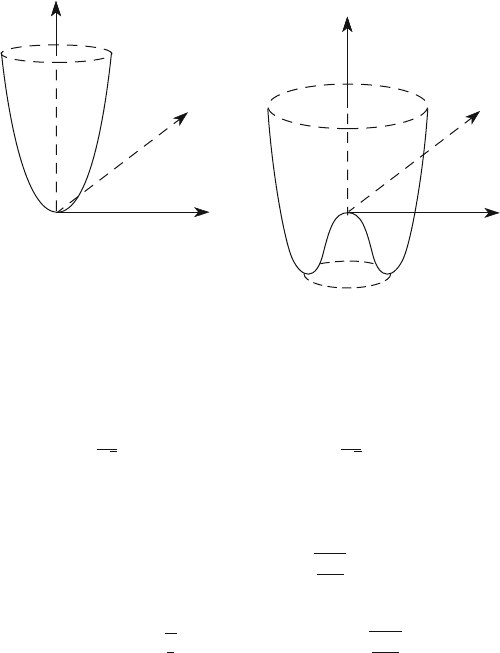
2
>0, the potential has a parabolic
shape, while for
2
<0, it has the form of a “Mexican hat,” as shown in Fig. 11.4.
In the latter case, the ground state with ' D 0 corresponds to a local maximum of
the potential and therefore to an unstable equilibrium.
This system is still invariant under global rotations, though not under local
rotations. The symmetry is broken by choosing ' as a complex doublet with a given
hypercharge .Y
W
D 1/:
' D
'
a
'
b
(11.40)
326 11 The Standard Model of the Microcosm
V(φ)
V(φ)
φ
2
φ
2
φ
1
φ
1
ab
Fig. 11.4 Higgs potential (11.39), as a function of
1
D Re./ and
2
D Im./.(a)For
2
>0,
V./has a parabolic shape with a minimum for V./ D 0 at
1
D
2
D 0.(b)For
2
<0,ithas
the form of a “Mexican hat”
where
'
a
D
1
p
2
.'
1
C i'
2
/'
b
D
1
p
2
.'
3
C i'
4
/:
(11.41)
Given that the Lagrangian density is invariant under gauge transformations and that
the ground state is a neutral state, we can choose the shape of the field ',and
particularly '
0
, in any space-time point x in order to have a down spinor of the
form
0
v
. With '
1
D '
2
D '
4
D 0 and '
3
D
q
2
2
, one has
'
0
D
q
1
2
0
v
with v D
q
2
(11.42)
where v is the vacuum expectation value of the Higgs field. In choosing one
particular minimum, the SU(2) symmetry has been spontaneously broken. The
ground state that is now different from zero is not isospin invariant. The Higgs field
' can be expanded around the ground state of the unitary gauge
' D e
i.x/
0
v C h.x/
: (11.43)
The real fields .x/ are excitations along the minimum of the potential. In the case
of global symmetry, they correspond to the so-called massless Goldstone bosons.In
local gauge theories, they may be eliminated by an appropriate rotation
'
0
D e
.x/
.x/ D
0
v C h.x/
: (11.44)
11.5 Spontaneous Symmetry Breaking. The Higgs Mechanism 327
It follows that the fields have no physical meaning as they disappear after a gauge
transformation. Only the real field h.x/ can be interpreted as a real particle, the
Higgs boson. The scalar field '.x/ can now be introduced into the gauge invariant
Lagrangian density (11.38) in order to determine the masses of the various bosons
by collecting all terms which are of second order in the fields A
a
,B
and h.These
bilinear terms can be extracted separately for the three Lagrangian densities defined
in Eq. 11.38. Taking into account the second order terms in the fields A
a
,B
and h
and neglecting higher order terms, the various contributions are:
1. The contribution from L
r
:
L
r
D .r
'/
C
.r
'/
2
d
order
!
1
2
.@
h/.@
h/
C
1
2
g
2
v
2
4
.A
1
A
1
C A
2
A
2
/
C
1
8
v
2
.gA
3
g
0
B
/.gA
3
g
0
B
/: (11.45)
2. The contribution from L
V
:
L
V
D V.'
C
'/
2
d
order
! constant C
1
2
.2
2
/h
2
: (11.46)
3. The contribution from L
YM
:
L
YM
2
d
order
!
1
4
A
a
A
a
1
4
G
G
(11.47)
where
A
a
@
A
a
@
A
a
: (11.48)
Since only second order terms are considered, F
a
is simplified in A
a
.
Since (11.45) contains mixed products of the gauge fields A
3
and B
, the corre-
sponding bosons cannot appear with a physical mass. Two orthogonal combinations
of A
3
and B
must be defined, that is,
Z
D cos
w
A
3
sin
w
B
(11.49)
A
D sin
w
A
3
C cos
w
B
(11.50)
where the so-called Weinberg angle
w
is the weak mixing angle chosen in a way
that the mixed products of Z
and A
disappear. Therefore,
tan
w
D
g
0
g
: (11.51)

328 11 The Standard Model of the Microcosm
Finally, the free Lagrangian density for all fields can be written as
L
H
D
1
2
.@
h/.@
h/
1
2
.2
2
/h
2
1
4
A
1
A
1
C
1
2
g
2
v
2
4
A
1
A
1
1
4
A
2
A
2
C
1
2
g
2
v
2
4
A
2
A
2
1
4
Z
Z
C
1
2
g
2
v
2
4cos
2
w
Z
Z
1
4
A
A
C 0A
A
(11.52)
CL
VVH
: (11.53)
The term L
VVH
described below (see (11.61)and(11.62)) contains mixed terms
hA
1
A
1
, hA
2
A
2
, hZ
Z
and hA
A
.
From the above equation, one sees that the Higgs mechanism allowed one to
associate massive particles to some of the gauge fields without having explicitly
introduced a mass term in the Lagrangian density (an operation which would not
have maintained the required symmetry). Mass terms have appeared implicitly and
the initial goal of describing the weak interaction via the exchange of massive vector
bosons has been achieved. The three mass terms are
m
2
W
D
g
2
v
2
4
for A
1
and A
2
(11.54a)
m
2
Z
D
g
2
v
2
4 cos
2
w
D
m
2
W
cos
2
w
for Z
(11.54b)
m
2
A
D 0 for A
: (11.54c)
There is one additional massive scalar particle (the multiplicative term in front of
the field h
2
), the Higgs boson H
0
with mass
m
H
0
D
p
2
2
D
p
2v: (11.55)
The gauge fields A
1
and A
2
can be replaced by the complex fields W
C
and W
respectively defined in (11.26)and(11.27).
• W
and W
C
are identified as the fields associated with the charged W
and W
C
bosons;
• Z
is identified as the field associated with the neutral Z
0
boson;
• The massless field A
is identified as the electromagnetic field associated with
the photon.
11.5 Spontaneous Symmetry Breaking. The Higgs Mechanism 329
Fig. 11.5 Geometrical
illustration of the relations
between the electroweak
coupling constants e, g,
g
0
,
w
g'
g
θ
W
e
Let us now consider the coupling constant of the massless field A
.From
Eqs. 11.49 and 11.50, one finds A
3
D A
sin
w
CZ
cos
w
and B
D A
cos
w
Z
sin
w
. Extracting the terms along the diagonal of (11.28) and expressing them as
functions of the fields A
and Z
as formulated above, we can write the following
identity as
gA
3
3
2
C
g
0
2
B
1 D g sin
w
Q A
C
g
cos
w
3
2
Q sin
2
w
Z
; (11.56)
defining Q
1C
3
2
. The coupling constant associated to the massless field A
(the
electric charge) is then identified to be g sin
w
. It follows that
g sin
w
D e: (11.57)
Figure 11.5 shows a geometrical illustration of the relations between the
electroweak coupling constants. The following important relations can therefore be
written as
tan
w
D
g
0
g
; sin
w
D
g
0
p
g
2
C g
02
; cos
w
D
g
p
g
2
C g
02
;eD
gg
0
p
g
2
C g
02
:
(11.58)
There is a deep connection between the coupling constants e, g and g
0
. The numeri-
cal value of the Weinberg angle was determined from: e scattering; the electroweak
interference in e
C
e
collisions; the precision measurement of the Z
0
; and the ratio
between the masses m
W
˙
and m
Z
0
. The most precise value of sin
2
w
is obtained
from the combination of all these measurements, obtaining sin
2
w
= 0.2319˙0
.0005 . From (11.54a)and(11.54b), one also has
m
W
D m
Z
cos
w
; sin
2
w
D 1
m
2
W
m
2
Z
: (11.59)
All these equations are valid at the fundamental level (“tree level”). They are
substantially modified by the radiative corrections which strongly depend on the
top quark mass and logarithmically on the Higgs boson mass.
Using Eqs. 11.8 and 11.54a, one can show that
v D .
p
2G
F
/
1
2
D 246 GeV: (11.60)
