Braibant S., Giacomelli G., Spurio M. Particles and Fundamental Interactions: An Introduction to Particle Physics
Подождите немного. Документ загружается.

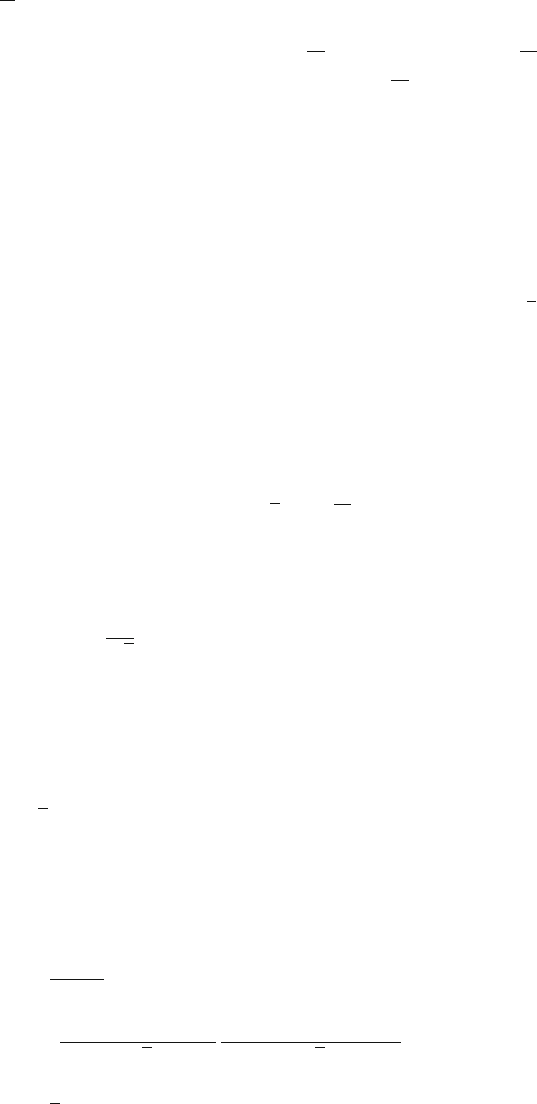
12.2 The K
0
K
0
System 351
beam is now composed of 50% of K
0
and 50% of K
0
, that is, it is as if the K
0
were “generated.” If this particle beam interacts with matter, the K
0
component will
be preferentially absorbed because it has a larger cross-section than for K
0
.Asa
consequence, the K
0
1
are regenerated.
The mathematical description of the time development of the K
0
beam requires
the use of complex amplitudes. The relative phase between K
0
1
and K
0
2
for a given
energy remains constant if the two particles have the same mass. However, K
0
1
and
K
0
2
have slightly different masses because of their difference in the weak coupling.
An analogous effect was found for the neutron and proton: they have different
masses due to the EM interaction.
The wave function of a steady state with mass m contains the phase term e
i
E
„
t
where E D mc
2
if the system is at rest. In the case of a state that decays with a
lifetime D„= , the wave function contains an additional phase factor e
t=2„
D
e
t=2
. The amplitude probability of such a wave function is thus proportional to
e
t=
(see discussion in Sect. 7.5). In the rest system (using here and later „Dc D
1,sothat D 1= ), the total phase of the wave function can be written as e
iMt
,
where M is the complex quantity M D m i=2. At the time t D 0,whenK
0
are
generated through Eq. 12.1,wehave
jK
0
.0/iDŒjK
0
1
.0/iCjK
0
2
.0/i=
p
2 IjK
0
.0/iD0: (12.8)
At time t, it evolves as
jK
0
1
.t/iDjK
0
1
.0/ie
iM
1
t
; jK
0
2
.t/iDjK
0
2
.0/ie
iM
2
t
(12.9a)
jK
0
.t/iD
1
p
2
jK
0
1
.0/ie
iM
1
t
CjK
0
2
.0/ie
iM
2
t
(12.9b)
with M
1
D m
1
i
1
=2 D m
1
i=2
1
, M
2
D m
2
i
2
=2 D m
2
i=2
2
; m
1
and
m
2
represent the masses of K
0
1
and K
0
2
,
1
and
2
their respective lifetimes.
As a consequence of (12.9), a series of interference effects appears: they are the
so-called strangeness oscillations. The intensity of the beam is given by the wave
function times its complex conjugate. Starting with a pure K
0
state, i.e., K
0
1
.0/ D
K
0
2
.0/ D K
0
.0/=
p
2, at the time t, one has
I
K
0
1
.t/ DhK
0
1
.t/jK
0
1
.t/iDhK
0
1
.0/jK
0
1
.0/ie
1
t
D I
1
.0/e
1
t
:
For the relative intensity of the K
0
, one has (remember that I
K
0
.0/ DhK
0
.0/j
K
0
.0/iD1)
P
K
0
!K
0
.t/ D
I
K
0
.t/
I
K
0
.0/
DhK
0
.t/jK
0
.t/iD
D
.hK
0
1
.t/jChK
0
2
.t/j
p
2
.jK
0
1
.t/iCjK
0
2
.t/i/
p
2
D
D
1
4
e
1
t
C e
2
t
C 2e
Œ.
1
C
2
/=2t
cos.m t/
(12.10a)
352 12 CP-Violation and Particle Oscillations
Fig. 12.2 Intensity
oscillations of K
0
and of K
0
,
starting from a pure K
0
state.
Equations 12.10a,bhave
been used with
m
K
=m
K
D 0:7 10
14
0.8
0.6
0.4
0.2
0
246810
K
0
Intensity
t/τ
K
1
0
K
0
where m D m
2
m
1
, I
K
0 .0/ D 0, I
K
0 .0/ D 1. In the last step, the property of
the complex exponential, e
iy
D cos y C i sin y, is used. Similarly, one has
P
K
0
!K
0
.t/ D
I
K
0 .t/
I
K
0 .0/
D
1
4
e
1
t
C e
2
t
2e
Œ.
1
C
2
/=2t
cos.m t/
:
(12.10b)
To illustrate the meaning of (12.10a, b), let us assume that K
0
and K
0
are stable
particles; this means (by definition of M
1;2
in (12.9)) that
1
D
2
D 0. It follows
that
P
K
0
!K
0
.t/ D
1
2
Œ1 C cos.mt/ D cos
2
mt
2
(12.10c)
P
K
0
!K
0
.t/ D
1
2
Œ1 cos.mt/ D sin
2
mt
2
: (12.10d)
At the initial time (t D 0), only K
0
are present; with increasing time (i.e.,
when particles move away from the production point), the probability of finding
K
0
increases. For t D =m (in natural units), only K
0
are present in the
beam; at t D 2=m, only K
0
are present. This is the phenomenon of particle
oscillations. The fact that
1
;
2
are nonzero real numbers causes the intensity
to exponentially decrease (as in the damped oscillatory phenomena), but does not
change the frequency of beats, which depends on m.
The time evolution of the K
0
and K
0
intensities is illustrated in Fig. 12.2.The
mass difference between K
0
1
and K
0
2
was found to be extremely small (m D 3:7
10
6
eV). Their lifetimes are instead very different:
K
0
2
' 600
K
0
1
, due to the
energy available in the phase space of the process, i.e., the kinetic energy available
in three-particle (K
0
2
! 3) or two-particle (K
0
1
! 2) decays. Since a small
CP-violation was experimentally found, the general framework is modified and the
above description is only approximately valid.

12.3 CP-Violation in the K
0
K
0
System 353
To understand how a mismatch of the waves may change the flavor eigenstate,
let us use an analogy. In optics, a distinction between “base colors” (for
instance red, blue and green) and “compound colors” can be made. For
example, purple is a mixture of red and blue. Now, imagine a given source of
a “purple wave.” Purple (corresponding in the analogy to a flavor eigenstate)
is obtained by mixing the red and blue basic colors (that correspond to
mass eigenstates). The emitted wave has a percentage of red and blue waves
with initial values in order to provide, in the mixture, the right shade of
purple. The propagation can affect the basic red and blue colors differently.
If they propagate with the same velocity, their overlap gives the same purple
color everywhere. If they propagate with different velocities, their intensity is
different from point to point. This corresponds to different resulting colors
seen by observers in different positions. The word “oscillation” does not
refer to the fact that particles are represented by waves, but rather that the
observable color (D flavor eigenstate) changes with the distance from the
source, with an oscillatory law. At certain points, the wave may even appear
to an observer as purely red (or blue).
12.3 CP-Violation in the K
0
K
0
System
In 1964, Cronin, Fitch (Nobel laureate in 1980) and colleagues experimentally
observed that a small K
0
2
fraction decays in 2. This is inconsistent with the
fact that K
0
2
is a CP eigenstate, as it should always decay into three pions. In
their experiment, a pure K
0
beam of 1 GeV/c momentum was injected into a
15 m length vacuum tube. All K
0
1
decayed before reaching the end of the pipe
since l
K
0
1
D ˇc
K
0
S
' 6 cm. At the end of the tube, only K
0
2
decays in 3
were expected. A few K
0
2
decays in
C
and
0
0
were also observed. This
result represented the first experimental evidence of CP-violation. Following this
observation, a slight modification is needed in the discussion presented above. The
particles with longer and shorter lifetimes were denoted as K
0
L
and K
0
S
respectively,
with
S
D .89:53 ˙0:05/ 10
12
sI
L
D .51:14 ˙0:21/ 10
9
s(L and S stand
for long and short). They are now considered as the mass eigenstates, leaving the
names K
0
2
, K
0
1
for the CP eigenstates [12B95]. In addition to the K
0
L
! 2 decay,
a charge asymmetry in the semileptonic decays of K
0
L
was also found, see (12.26).
The K
0
K
0
propagation represents a very precise interferometer, which can
highlight the small CP-violation in the K
0
L
system. Due to the relevant historical
point of view, the K
0
K
0
system is used in the following to describe the time
evolution formalism needed to extract the small quantities producing CP-violation.
The formalism can easily be generalized for other mesons made of heavier quarks,
as the more recently experimentally studied D; B; B
S
mesons.
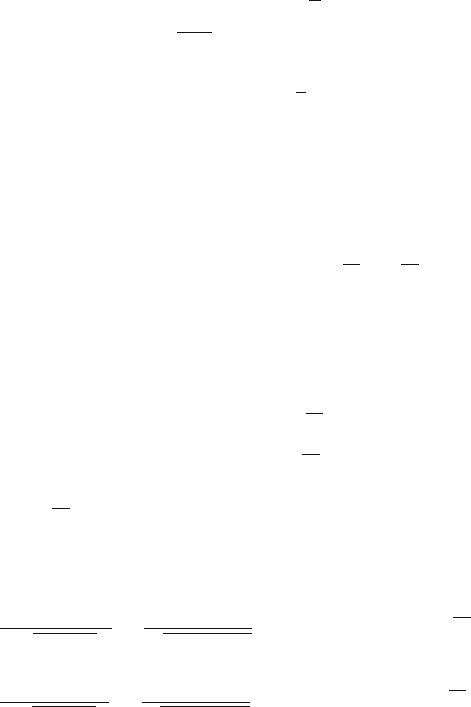
354 12 CP-Violation and Particle Oscillations
12.3.1 The Formalism and the Parameters of CP-Violation
The CP-violation can be included in the basic equations of meson oscillations
assuming that the Hamiltonian of the weak interaction is not invariant under CP.The
formalism presented in Sect. 12.2 can be generalized: the Hamiltonian eigenstates
are not eigenstates of the CP operator and the physical states are a superposition of
states with CP eigenvalues C1and1.
The time evolution of the system D
K
0
K
0
(eigenstates for the strong
interaction) is given as usual by i
@ .t/
@t
D H .t/, with
H D M D m
i
2
(12.11a)
or in the explicit form:
M D
m
11
i
11
=2 m
12
i
12
=2
m
21
C i
21
=2 m
22
i
22
=2
: (12.11b)
Due to the CPT invariance, one has hK
0
jM jK
0
iDhK
0
jM jK
0
i, m
11
D m
22
and
11
D
22
.IfCP is conserved, one has m
12
D m
12
and
12
D
12
, yielding to the
already obtained Eqs. 12.10a,b.
The two eigenstates of the new Hamiltonian (12.11a) are called the mass
eigenstates, namely,
jK
0
S
iDpjK
0
iCqjK
0
i (12.12)
jK
0
L
iDpjK
0
iqjK
0
i: (12.13)
Since jK
0
i and jK
0
i are linear combinations of CP eigenstates jK
0
1
i and jK
0
2
i
(12.6b), the mass eigenstates can also be expressed as linear combinations of CP
eigenstates
jK
0
S
iD
jK
0
1
iC"jK
0
2
i
p
1 Cj"j
2
D
1
p
2.1 Cj"j
2
/
h
.1 C "/jK
0
iC.1 "/jK
0
i
i
(12.14)
jK
0
L
iD
jK
0
2
i"jK
0
1
i
p
1 Cj"j
2
D
1
p
2.1 Cj"j
2
/
h
.1 C "/jK
0
i.1 "/jK
0
i
i
: (12.15)
If CP is conserved, one must have " D 0 (or p D q)andjK
0
S
iDjK
0
1
i,
jK
0
L
iDjK
0
2
i.
The " parameter is a complex number (" Dj"je
i'
) representing the deviation of
K
0
L
and K
0
S
from CP-eigenstates, i.e., the degree of CP-violation.

12.3 CP-Violation in the K
0
K
0
System 355
K
0
s
u, c, t
d
sd
W
+
W
–
WW
d
–
d
–
s
–
u
–
,
c
–
,
t
–
u
–
,
c
–
,
t
–
s
–
u, c, t
V
ud
,V
cd
,V
td
V
*
us
,V
*
cs
,V
*
ts
K
0
K
0
K
0
a
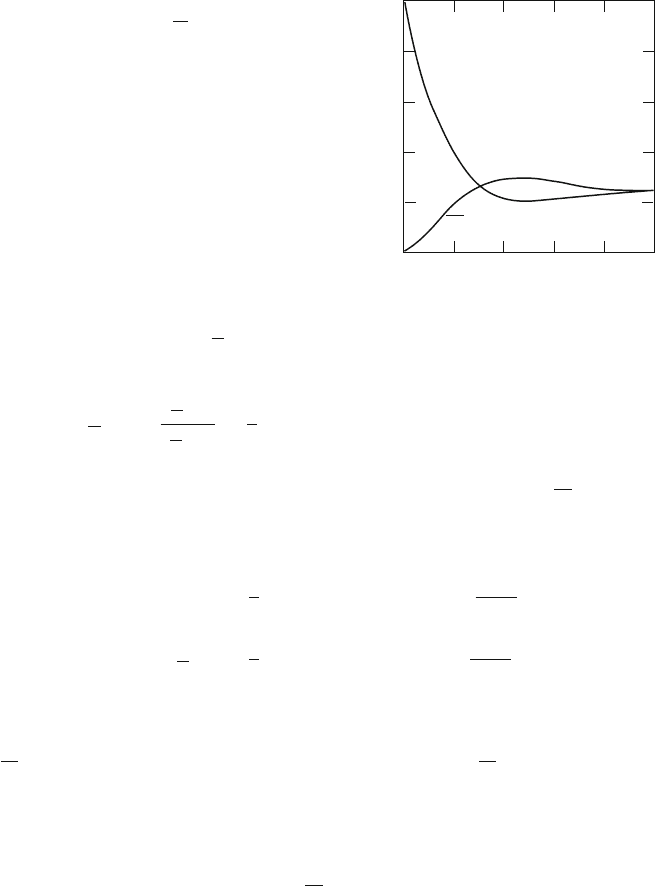
b
Fig. 12.3 (a), (b) Box diagrams illustrating the K
0
$ K
0
transitions with S D 2. Note the
matrix elements V
ud
; :::; V
us
; :::. With two exchanged W , these processes are of second order for
the weak interaction
12.3.1.1 Direct and Indirect CP-Violation
The K
0
L
decay into 2 occurs via CP-violation in the mixing of the strong
interaction eigenstates during their propagation. This implies a second order process
in terms of the weak interaction coupling constant (the exchange of two W vector
bosons is needed, with a S D 2 strangeness change). The corresponding Feynman
diagrams are the so-called box diagrams shown in Fig.12.3.TheCP-violation with
S D 2 is called indirect. It is measured by the (complex) quantity " in (12.14)and
(12.15).
The CP-violation can also occur through a term in the Hamiltonian (and,
consequently, in Feynman diagrams) with S D 1, i.e., a single “conversion” of
the type s ! d. This transition occurs with the so-called penguin diagram shown in
Fig. 12.4, dominated by the exchange of a t quark. This figure actually represents a
set of three diagrams because the gluon exchanged at the bottom of the diagram can
be replaced by a photon or a Z
0
. The diagram with a gluon exchange is dominant
since ˛
s
˛
EM
;˛
WI
.However,fortop mass m
t
' 180 GeV, the probability of a
Z
0
exchange increases and interferes destructively with the exchange of gluons. For
this reason, the penguin diagram contribution to CP-violation is relatively small. It
is measured by the (complex) quantity "
0
defined below. The CP-violation due to
S D 1 transitions is called direct.
From the experimental point of view, the direct and indirect CP-violation can be
highlighted both in nonleptonic decays and in semileptonic decays of mesons.
Nonleptonic decays. Let us consider the nonleptonic decay amplitudes A.K
0
!
/ DhK
0
! j, A.K
0
! / DhK
0
! j. The amplitude ratios for
C
and
0
0
decays are respectively
C
Dj
C
je
i'
C
D
A.K
0
L
!
C
/
A.K
0
S
!
C
/
(12.16)
00
Dj
00
je
i'
00
D
A.K
0
L
!
0
0
/
A.K
0
S
!
0
0
/
: (12.17)
356 12 CP-Violation and Particle Oscillations
Fig. 12.4 Penguin diagram
illustrating transitions with
S D 1 (s ! d ) whose
probability amplitude
contains a term that produces
asmallCP-violation
s
d
W
g
d
–
d
–
u, c, t
It can be shown [P08] that these ratios are related to both CP-violation parameters
" and "
0
,thatis,
C
Dj
C
je
i'
C
D " C "
0
(12.18)
00
Dj
00
je
i'
00
D " 2"
0
(12.19)
where j"jj"
0
j. Experimentally, both the intensity and the phase of the amplitudes
(12.16)and(12.17) can be measured through the interference of decays in
C
(and in
0
0
) as a function of proper time. The observable quantity is the asymmetry
defined as
A
.t/ D
P
K
0
!
.t/ P
K
0
!
.t/
P
K
0
!
.t/ C P
K
0
!
.t/
(12.20)
where P
K
0
!
.t/ hK
0
! jK
0
i and P
K
0
!
.t/ hK
0
! jK
0
i;after
some algebra, from (12.20), one can derive
A
.t/ D 2Re" C
2j
je
Œ.
S
L
/t=2
1 Cj
j
2
e
Œ.
S
L
/t
cos.m t '
/: (12.21)
Here, ( stands for both
0
0
or
C
). Figure 12.5 shows an example of such
an interference in the
C
decay channel. Since (12.14)and(12.15) are not CP
eigenstates, we may imagine that the component, which still decay into 2,isthe
K
0
1
.TheK
0
L
state contains a small fraction of K
0
1
(12.15), and this tiny fraction
decays into 2. From experiments carried out at CERN, Brookhaven, Argonne and
SLAC laboratories, it was measured that j"j'2:3 10
3
and ' 45
ı
(i.e., Re " '
Im ").
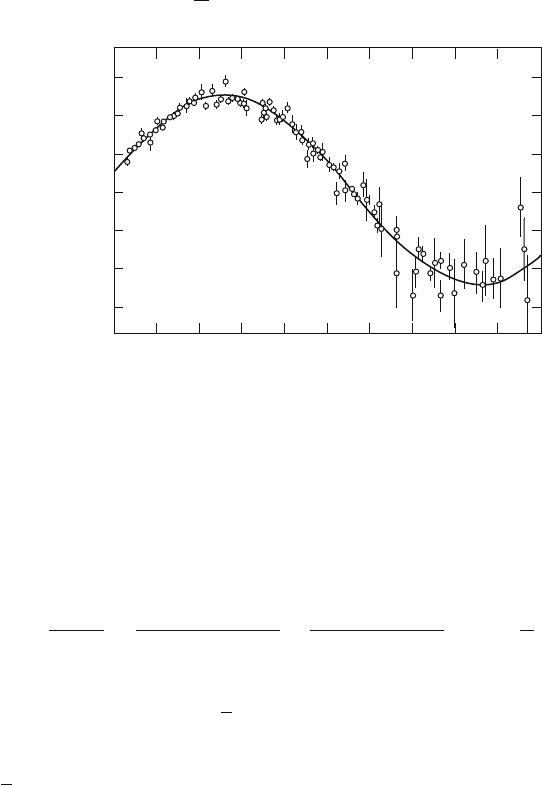
12.3 CP-Violation in the K
0
K
0
System 357
1.2
0.8
0.4
0
012345678910
–0.8
–0.4
–1.2
Proper time (10
–10
s)
Time interference
Fig. 12.5 Time interference (asymmetry) in the decay of K
0
L
and K
0
S
in
C
as a function of
the K
0
S
proper time (see Eq. 12.20)
While it has been known since 1964 that j"j >0, for many years, there were
experimental discrepancies about the fact that "
0
was different from zero. Today
[P08], the issue is solved. The ratio "
0
=" was determined by measuring the double
ratio R (Problem 12.4)
R D
j
00
j
2
j
C
j
2
D
.K
L
!
C
/
.K
S
!
C
/
.K
L
!
0
0
/
.K
S
!
0
0
/
' 1 6
"
0
"
: (12.22)
A few years ago, two high precision experiments (KTeV at Fermilab and NA48 at
the CERN SPS) measured Re(
"
0
"
) with an accuracy of the order 2 10
4
.Both
experiments measured the K
0
S
and K
0
L
decays into
C
and
0
0
,derivingthe
result through the relation (12.22). The two experiments agreed on the value of
Re(
"
0
"
), finally proving the existence of direct CP-violation. It was found [P08] that
j
C
jD.2:233 ˙0:010/ 10
3
'
C
D .43:52 ˙ 0:05/
ı
j
00
jD.2:222 ˙ 0:010/ 10
3
'
00
D .43:50 ˙ 0:06/
ı
(12.23)
From (12.18), (12.19)and(12.22), it was obtained that
j"jD.2:229 ˙ 0:010/ 10
3
(12.24)
Re."
0
="/ D .1:65 ˙ 0:26/ 10
3
: (12.25)

358 12 CP-Violation and Particle Oscillations
Here, we briefly discuss the experimental setup of the NA48 experiment at
CERN. It simultaneously used two nearly collinear K
S
and K
L
beams and
measured the four decay channels that appear in the ratio R of (12.22). The
two beams were produced by 450 GeV protons from the SPS. Because of the
different average decay lengths of 110 GeV/c momentum K
L
.
L
D 3:4 km/
and K
S
.
S
D 5:4 m/,theK
L
and K
S
were produced in two separate targets
at 126 m and 6m before the beginning of the decay region, respectively. Each
proton pulse [about 10
12
protons per impulse (ppi) of 2.4 s] was divided in
two. Most protons were hitting the first target: the K
S
decayed rapidly, and
from the first target, there were about 10
7
K
L
per pulse directed to the decay
region. A small fraction of protons (about 3 10
7
ppi) arrived at the second
target, where a beam of about 10
2
K
S
per pulse was produced.
The K !
C
decays were measured with a spectrometer that used a
magnet and a drift chamber system. For K !
0
0
decays, the ’s from
the
0
decay were measured in a 10 m
3
homogeneous calorimeter filled with
liquid krypton. This detector was highly segmented, with an energy resolution
of better than 1% at energies above 10 GeV and a time resolution of 1 ns.
Nonleptonic decays. The semileptonic decay is a channel that can be studied by
measuring the asymmetry (l stands for muon or electron), that is,
A
L
D
.K
L
!
l
C
l
/ .K
L
!
C
l
l
/
.K
L
!
l
C
l
/ C .K
L
!
C
l
l
/
: (12.26)
Taking the sign of the lepton charge as a reference, a nonzero A
L
value shows in
an independent way that the K
L
decay into “matter” and “antimatter” is different.
In terms of the CP-violation parameters (see Problem 12.5), the measurements
(averaged between muons and electrons) provide
A
L
' 2Re."/ D .3:32 ˙ 0:06/ 10
3
; (12.27)
which is consistent with what is obtained for the nonleptonic decays.
12.4 What is the Reason for CP-Violation?
Within the Standard Model, the CP-violation is introduced through the so-called
Kobayashi–Maskawa mechanism which predicts the existence of a phase factor in
the 3 3 matrix (8.62b). The nonzero value of the phase is the dominant source of
CP-violation in meson decay.

12.4 What is the Reason for CP-Violation? 359
Remember that the mixing of the three quark generations in the weak interaction
is described by the 3 3 matrix called the Cabibbo–Kobayashi–Maskawa (CKM
matrix). The probability of each possible quark flavor transition due to WI is
therefore specified by the CKM matrix (see Chap. 8). For example, the square of
the matrix element V
ud
gives the probability that a up quark turns into a down
quark. The weak interaction between antiquarks is ruled by the complex-conjugated
CKM matrix. If the CKM matrix does not contain imaginary elements (i.e., all real
elements), quarks and antiquarks would behave exactly in the same way for the WI.
The nine elements of the CKM matrix are not independent. For example, an up-
type quark can only convert via W
C
exchange into one of the three quarks with
1/3 electric charge (i.e., d;s;b); the sum of the three probabilities must be equal
to one. Under these constraints, the CKM matrix can be expressed in terms of only
four parameters: three real numbers for the mixing angles, and one imaginary phase,
which makes the CP-violation possible.
In Chap. 8, two possible parameterizations of the CKM matrix were presented.
A widely used approximation of the CKM matrix (8.67) is the Wolfenstein
parametrization which displays the hierarchy of the three mixing angles
12
;
23
;
13
,
which have
1
s
12
s
23
s
13
. The sine of the Cabibbo angle s
12
D .' 0:23/
can be used as an expansion parameter (i.e., the other elements can be expressed in
terms of powers of ):
V D
0
@
V
ud
V
us
V
ub
V
cd
V
cs
V
cb
V
td
V
ts
V
tb
1
A
D
0
@
1
1
2
2
A
3
. i/
1
1
2
2
A
2
A
3
.1 i/ A
2
1
1
A
C O.
4
/
(12.28)
where A; ; are real numbers and represent (with ) the four independent
parameters of the matrix. In particular, is the CP-violating phase.
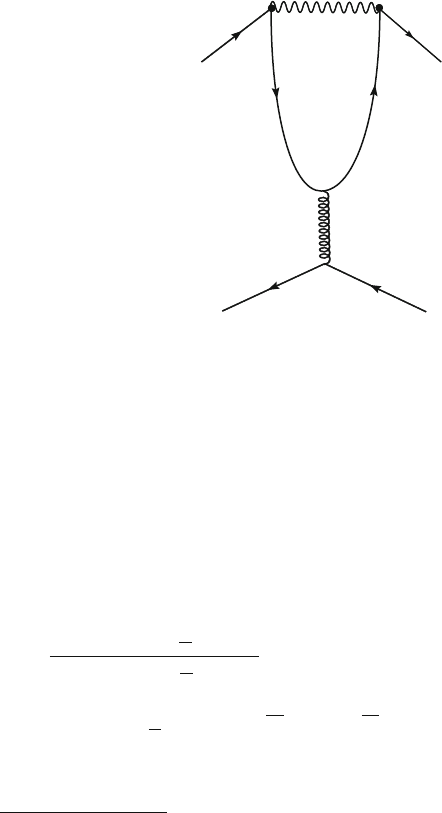
A simple way to visualize the relations between the elements of the CKM matrix
was proposed by J. Bjorken and C. Jarlskog in 1988 through the so-called unitarity
triangle. The request that the CKM matrix is unitary leads to relations between its
elements, for example,
V
ud
V
ub
C V
cd
V
cb
C V
td
V
tb
D 0: (12.29)
Each term of (12.29) is a complex number that can be represented in a Cartesian
plane: the real part is represented along the x-axis and the complex part is the
ordinate. The sum behaves exactly as the sum of three vectors adding to zero:
drawing a triangle in the xy-plane, the tip of the third vector ends where the first
begins. The three angles (called ˛; ˇ; ) and the length of the sides correspond to
relations between elements of the CKM matrix (see Fig. 12.6). The height of the
triangle depends on the value of the imaginary phase in (12.28). If D 0,thethree
summands in (12.29) are real numbers and the triangle degenerates to a segment
along the x-axis.
1
Here, as elsewhere, we use the notation s
12
D sin
12
;c
12
D cos
12
,etc.

360 12 CP-Violation and Particle Oscillations
α
β
γ
(0,0) (1,0)
(ρ, η)
B D
*
π, DK, πK, ...
B
0
ππ, ρπ, ...
B
0
J/ψ K
S
, D*D
–
*, ...
V
*
ub
V
ub
V
cd
V
*
cb
V
td
V
*
tb
V
cd
V
*
cb
R
u
R
t
Fig. 12.6 Unitarity triangle. Inner angles ˛; ˇ; can be determined from measurements of CP-
violation in decays of mesons with a b quark. The R
u
side is defined as the edge between the ˛
and angles and the R
t
side is defined as the edge between the ˛ and ˇ angles
The values of the CKM matrix elements are such that a larger degree of CP-
violation is expected for mesons with a bottom quark with respect to the neutral
kaons system. This implies that particles with a b quark behave differently than
antiparticles with a
b antiquark.
Early studies on B
0
B
0
mixing were carried out by UA1 at the CERN Sp pS
collider, ARGUS at DESY and by the LEP experiments. Thanks to precision
measurements performed at B-factories (see next section), the predictions of the
Standard Model were verified with a high degree of accuracy. The CP-violation
observed in the B
0
B
0
system is compatible with the parameter obtained from
the K
0
K
0
system. However, some pieces of the puzzle are still not understood,
for example, the degree of CP-violation is in fact not large enough to explain the
observed asymmetry between matter and antimatter in the universe.
12.5 CP-Violation in the B
0
B
0
System
The formalism introduced for the K
0
K
0
system can be applied to the B
0
B
0
case. There are two types of B
0
mesons: the “normal” B
0
d
and the “strange” B
0
s
,
that is,
B
0
d
D bd ; B
0
d
D bd (12.30)
B
0
s
D bs ; B
0
s
D bs: (12.31)
Let us consider the B
0
d
B
0
d
system (denoted as B
0
B
0
to simplify the notation).
Transitions B
0
$ B
0
can occur via the diagrams of Fig. 12.7. As for the neutral K
