Braibant S., Giacomelli G., Spurio M. Particles and Fundamental Interactions: An Introduction to Particle Physics
Подождите немного. Документ загружается.

10.5 Cross-Section for CC
N Interactions 289
reaction which occurs through an initial state with angular momentum J D 1.The
conservation of the third component of the angular momentum allows the transition
only to one of the possible .2J C 1/ D 3 substates. The cross-section is thus
suppressed by a factor of 1/3 with respect to that of the J D 0 state. Integrating
on y, one has
d
;
dx
D
0
2
E
1
3
F
2
.x/ xF
3
.x/
C
F
2
.x/ ˙ xF
3
.x/
: (10.69)
The integration on the variable x of the terms within the curly braces of (10.69)
gives a constant. Thus, the total cross-section for (and
) is linearly dependent on
the energy E
. The proportionality constant is determined by the measurement of
the structure functions F
2
;F
3
. For neutrinos, one has
N
D a
N
E
D .0:667 ˙ 0:014/ 10
38
cm
2
GeV
E
.GeV/: (10.70)
For antineutrinos, one has:
N
D a
N
E
D .0:334 ˙ 0:008/ 10
38
cm
2
GeV
E
.GeV/: (10.71)
Using relations (10.67c) and (10.67d), and the integral on the variable y, it can be
shown that the ratio
N
N
D 2.From(10.60, 10.61), one has
Z
d
2
dx dy
dx dy D
0
Z
Œxq.x/ C x
q.x/.1 y/
2
dx dy
D
0
0:3 C 0:06
1
3
D 0:32
0
(10.72a)
Z
d
2
dxdy
dx dy D
0
Z
Œxq.x/.1 y/
2
C xq.x/dx dy
D
0
0:3
1
3
C 0:06
D 0:16
0
; (10.72b)
in good agreement with the experimental results. Figure 10.12 shows the depen-
dence on E
of the ratio
CC
tot
=E
D a
for neutrinos and antineutrinos. These
relations are constant up to E
lab
' 250 GeV. It is believed that the cross-sections
N increases linearly with energy up to
p
s m
W
in the c.m. system. For higher
energies, the cross-sections must take into account the W vector boson mass in the
bosonic propagator, as discussed in Chap.11.

290 10 High Energy Interactions and the Dynamic Quark Model
Average σ
T
/E
ν
(approx. 20-25 GeV)
0.67
0.34
νΝ
νΝ
0 10 20 30 50 100 150 200 250
E
ν
(GeV)
σ
T
/E
ν
×10
–38
cm
2
/ GeV
1.0
0.8
0.6
0.4
0.2
Fig. 10.12 Ratio between the total cross-section and E
for the processes
N and
N as a
function of the neutrino energy E
in the laboratory system. The ratios a
N
D
CC
tot
=E
and
a
N
D
CC
tot
=E
are constant [P08]
10.6 “Naive” and “Advanced” Quark Models
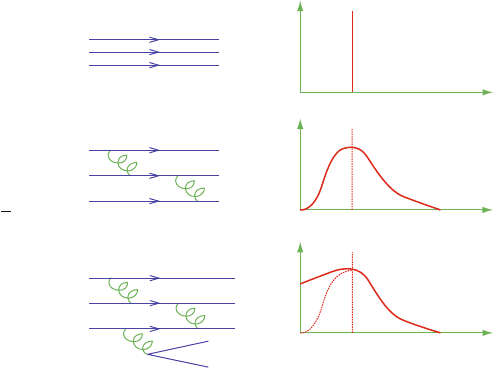
The structure functions have been measured with great precision in various ex-
periments and in a wide range of parameters x;Q
2
;W. In particular, the H1 and
ZEUS experiments at the ep collider HERA at DESY produced an impressive
series of results, whose importance can be appreciated by comparing the HERA
F
2
.x/ measurements shown in Fig. 10.16 and the earlier DIS measurements shown
in Fig. 10.9.
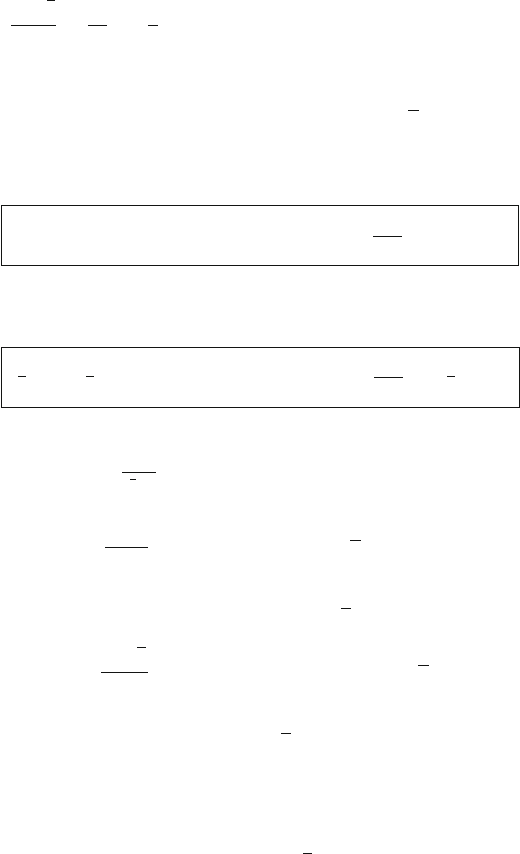
In the static quark model (which assumes three noninteracting valence quarks),
the structure function F
2
, as measured by an ideal experiment with infinite reso-
lution, would be equal to the one shown in Fig.10.13a. Each parton carries 1/3 of
the nucleon momentum. When interactions between quarks through the exchange of
gluons are considered, each quark carries a larger or smaller fraction of the proton
momentum compared to the previous democratic division. The F
2
.x/ is similar to
that in Fig. 10.13b. Finally, if the creation of q
q virtual pairs by soft gluons radiated
by each valence quark is included, a F
2
.x/ similar to that sketched in Fig. 10.13c
would be expected. The q
q pairs carry a small fraction of the nucleon momentum.
10.6.1 Q
2
-Dependence of the Structure Functions
Early experiments indicated that the structure functions do not vary with Q
2
(scaling
invariance or Bjorken scaling). The measurements performed in experiments at
CERN and Fermilab in the late 1970s showed that F
2
.x/ startedtopresenta
10.6 “Naive” and “Advanced” Quark Models 291
Fig. 10.13 Schematic
interpretation of the F
2
.x/
function. From the top:
(a) Three noninteracting
quarks carrying exactly
x D 1=3 of the nucleon
momentum; (b) interactions
between quarks produce
variations of the fraction x of
the carried momentum;
(c) quarks create, through
gluon radiation, virtual q
q
pairs carrying a small x
3 free quarks
3 bound quarks
3 bound quarks
+ emitted gluons
1/3
1
F
2
F
2
x
x
x
1/3 1
1/3 1
a
b
c
dependence on Q
2
with gradually increasing energy. This violation of the scaling
invariance (the scale breaking effect), shown in Fig.10.14, was attributed to effects
due to the strong interaction. In particular, F
2
.x/ increases with Q
2
at low x,the
region where the contribution of sea quarks is dominant. It decreases with Q
2
at
large values of x, where the contribution of valence quarks is prevailing. When the
transferred four-momentum Q
2
increases, the resolving power to study the nucleon
structure improves. The contribution of partons with large momentum fraction
.x > 0:25/ and interacting through electromagnetic or weak interactions decreases,
while the number of partons with small momentum .x < 0:15/ increases. For
0:15 < x < 0:25, the Bjorken scaling law is satisfied with a good approximation.
In addition to the violation of Bjorken scaling, the “naive” parton model is unable
to explain the production of hadrons with large transverse momentum with respect
to the direction of the virtual boson, and events with multiple jets of hadrons.
The coupling constant ˛
S
depends on Q
2
and can be determined from the
Q
2
dependence of the structure functions. The scale breaking is explained in the
“advanced” quark-parton model, where quarks are strongly interacting. For Q
2
2
QCD
' .200 MeV/
2
(see Sect. 11.9.2), ˛
S
is small and perturbation expansions
can be used to compute physical quantities, for example, cross-sections. For small
Q
2
, ˛
S
becomes large.
The dependence on the energy scale of the quark density functions has the
following interpretation: when Q
2
increases, the spatial resolution of the virtual
boson probing the proton improves. At high Q
2
, one can probe the cloud of partons
surrounding each quark. The radiation of a high energy gluon gives rise to a jet of
hadrons (as shown in Fig. 10.15c). This is an easily detectable event topology which
is not explained in the simplest model of noninteracting quarks.
In ep ! e CX collisions with small values of the Bjorken variable x.x<10
3
/,
the main contribution to the inelastic cross-section is the interaction of the virtual
photon with a sea quark. The structure functions at small x mainly depend on
292 10 High Energy Interactions and the Dynamic Quark Model
Q
2
(GeV
2
)
F
2
(x, Q
2
) + c(x)
H1
ZEUS
BCDMS
E665
NMC
SLAC
0
1
2
3
4
5
6
7
8
9
10
10
–1
1 10 10
2
10
3
10
4
10
5
10
6
Fig. 10.14 The proton structure function F
p
2
as a function of the transferred four-momentum
squared Q
2
for fixed values of x. F
p
2
was obtained from measurements of deep inelastic ep
scattering in the HERA kinematic domain (x > 0:00006) and for electron (SLAC) and muon
scattering on a fixed target (BCDMS,E665,NMC). Note that the ordinate for each value of x are
offset by a factor c.x/ for clarity [10P02]
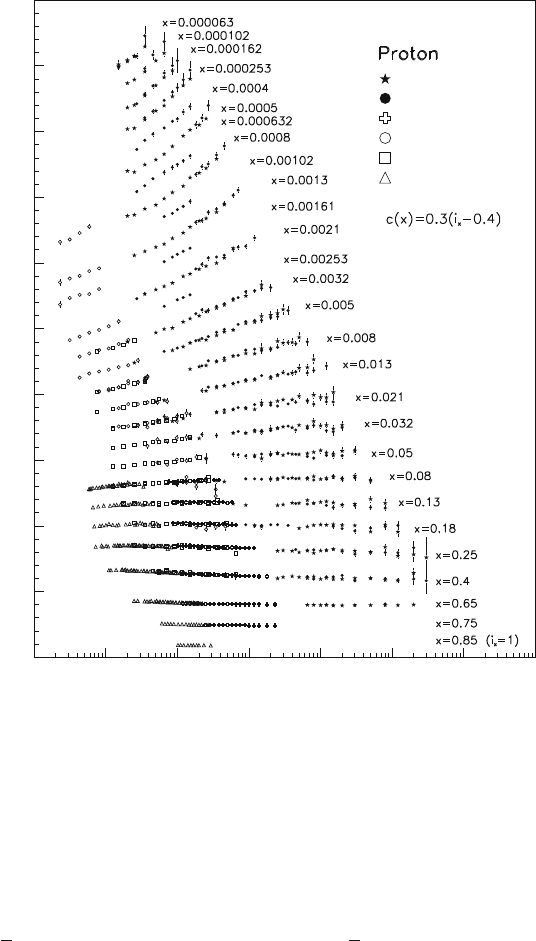
sea quark and gluon distributions. The number of virtual pairs increases when the
fraction x of the momentum that they carry decreases. This yields an increase of the
function F
2
in the small x limit. The expected behavior for the gluon (xg)andsea
quark (x
q) distributions is of the type xg ' x
1
, xq ' x
2
(see Fig. 10.16); this
parametrization was confirmed by the data collected at HERA.
Fragmentation of the hadronic system. The single inclusive reaction a C b !
c C X requires the presence of the specific c hadron in the final state, regardless of
the remaining system X. Its cross-section is defined by the c.m. energy and by the

10.6 “Naive” and “Advanced” Quark Models 293
e
ab c
e
q
p
γ, Z
γ
e
ν
q
p
W
±
e
e
q
g
p
Q
Q
Q
–
Fig. 10.15 Lowest order Feynman diagrams for the three basic processes of inelastic ep scatter-
ing: (a) NC scattering, (b) CC, (c) through photon–gluon fusion
kinematic variables x and Q
2
. If the two stages of the process are really independent,
the cross-section for the inclusive single process can be factorized as
d
3
dx dQ
2
dz
' F.x;Q
2
/D.z;Q
2
/ (10.73)
with F.x;Q
2
/ ' F.x/, D.z;Q
2
/ ' D.z/ if the “scale breaking effect” is not
considered. The properties of the hadronic system produced in lepton–nucleon
collisions, are described by the fragmentation function D.z;Q
2
/; they are related
to the strong interaction hadronization process. The situation is very similar for
high energy hadron-hadron and e
C
e
collisions. For example, the fragmentation
function of a quark q into a pion is defined as
D
q
.z/ D
1
N
dN
d z
(10.74)
where z D E
= D E
=E
q
is the fraction of the energy transferred from the quark
to the final pion. The variable z for the fragmentation function has a role similar to
that of the variable x for the structure functions.
In the asymmetric HERA collider, 27.5 GeV electrons or positrons collided
head-on with 820 GeV protons (
p
s ' 300 GeV). Between 1992 and 2000,
HERA collected an integrated luminosity of about 130 pb
1
, producing
detailed results on the proton structure functions, the production of heavy
quarks, on diffraction and generally on QCD. After a major upgrade, the lu-
minosity increased by a factor of 5 and the lepton beams could be polarized
longitudinally. The HERA collider was operated in this configuration from
the end of 2003 until 2007. The collisions were recorded by two large 4
detectors: H1 and ZEUS. The beam asymmetry was reflected in the detector
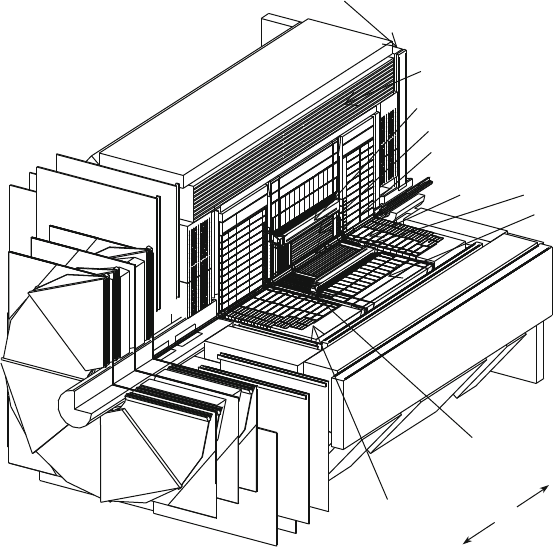
layout. Figure 10.17 shows the ZEUS detector. Schematically, it consisted
294 10 High Energy Interactions and the Dynamic Quark Model
x
F
2
(x, Q
2
)
H1
ZEUS
BCDMS
NMC
SLAC
E665
0.2
0.4
0.6
0.8
1
1.2
1.4
10
–4
10
–3
10
–2
10
–1
1
Fig. 10.16 The structure function F
p
2
as a function of the variable x for two values of Q
2
(3.5 GeV
2
and 90 GeV
2
), together with a parametrization obtained using a QCD-evoluted model
[10P02]
of (1) a set of detectors to measure the trajectory of charged particles in a
magnetic field; (2) a sampling calorimeter with uranium-scintillator plates,
serving as both electromagnetic (first part) and hadronic calorimeters; (3) an
iron absorber (the return yoke of the magnetic field); (4) the muon detectors,
before and after the iron absorber; (5) a forward detector, in the direction of
the proton beam, to measure the “leading protons.” The luminosity monitor
was a small angle radiation detector along the direction of the leptons,
measuring the ep ! ep bremsstrahlung. The cross-section for this process
is linearly correlated with the total number of e
C
.e
/ crossing the interaction
point.
10.6.2 Summary of DIS Results
Let us briefly recall the main results obtained on lepton–nucleon scattering. The
elastic e
– nucleus scattering at relatively low energy probed the distribution
10.6 “Naive” and “Advanced” Quark Models 295
FMUON
BMUON
FDET
BAC
RMUON
BEAMPIPE
BCAL
RCAL
SOLENOID
RTD
CTD
VXD
FCAL
2 m
Fig. 10.17 Layout of the ZEUS detector operated at the HERA collider at DESY, Hamburg
of electric charge inside the nuclei, and revealed details of the nuclear structure.
The observation of nearly elastic peaks in the inelastic electron-nucleus collision
demonstrated the presence of constituents, the nucleons, inside the nuclei. High
energy deep inelastic scattering in electron-, muon- and neutrino-nucleon interac-
tions revealed that the proton and the neutron are composed of fractionally charged
quarks, and that the neutron is not uniformly electrically neutral. Detailed analysis
showed that the proton and the neutron contain, in addition to the valence quarks,
sea quark-antiquark pairs. Finally, the nucleons must contain neutral constituents
with integer spin, the gluons, carrying about half of the nucleon momentum.
With the HERA collider, an accurate study of structure functions at small x was
performed. Figure 10.18 qualitatively illustrates what leptons “see” regarding the
proton structure when increasing the resolving power. Take note that the increase of
the parton number as x decreases. Amongst several other effects not discussed here,
we can briefly mention the study of polarization effects performed with polarized
muons and electrons colliding with polarized protons. These studies showed that the
quarks contribute 25% to the proton spin and that the remaining contribution must
come from the gluons.
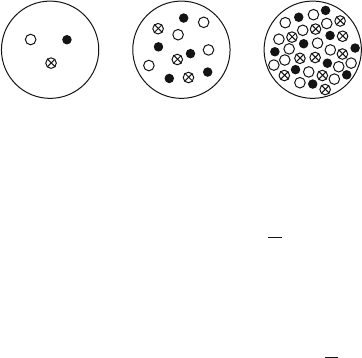
296 10 High Energy Interactions and the Dynamic Quark Model
Fig. 10.18 Qualitative
illustration of the density of
partons in the proton for
different values of the
variable x
x = 0.1 x = 0.001
x<x
c
10.7 High Energy Hadron-Hadron Collisions
In the following, we shall consider hadron collisions (mainly, pp and pp)atc.m.
energies above 10 GeV. For c.m. energies below 3 GeV (Sect. 10.4), there is the
resonance region. The total and elastic cross-sections vary rapidly and are charac-
terized by peaks whose height decreases with increasing energy. For c.m. energies
between 3 and 10 GeV, the cross-sections first decrease monotonically, reach a
minimum and then increase, see Fig. 10.19.ForE
cm
>10GeV (20 GeV for pp),
the total cross-section increases logarithmically with energy. This was discovered
in the early 1970s, first in K
C
p interactions at Serpukhov, Russia, followed by pp
interactions at the Intersecting Storage Rings (ISR) at CERN, and then with many
other experiments at Fermilab in the United States. It is still not completely clear as
to why the total hadron-hadron cross-sections increase with energy.
The differential elastic cross-section increases at low transferred momentum: this
elastic peak becomes narrower with increasing energy. At high energies, inelastic
processes are dominant and the average charge multiplicity (i.e., the average number
of produced charged hadrons) increases logarithmically with c.m. energy.
Figure 10.20 schematically illustrates the various types of processes: elastic colli-
sion, single and double diffractive scattering, and inelastic collisions. The diffractive
cross-section has characteristics similar to those of elastic scattering. The inter-
pretation is that both the elastic and the diffractive scattering are mediated by the
exchange of a pomeron, a pseudo-particle with the quantum numbers of the vacuum.
Low transverse momentum elastic, diffractive and inelastic scatterings are de-
noted as ln s processes. They are characterized by relatively large cross-sections
varying slowly with energy, as ln s. In contrast, the high transverse momentum
processes (high-p
t
processes) discussed in the previous sections have relatively
small cross-sections, rapidly varying with energy. It is conceivable that in ln s
processes, hadrons in their entirety are involved, while high-p
t
collisions occur
between the parton constituents. While perturbation methods can be used in high-p
t
strong interaction reactions, a different approach must be used for low-p
t
processes
due to the large value of the strong coupling constant. For this reason, phe-
nomenological models based on many-body QCD were developed. These models
use interpolation/extrapolation of data and explain many important aspects of the
secondary particle production, but sometimes have contradictory aspects. The low-
p
t
models can be used to extrapolate predictions on the characteristics of secondary
particles produced at LHC or by cosmic ray interactions in the atmosphere [G90].
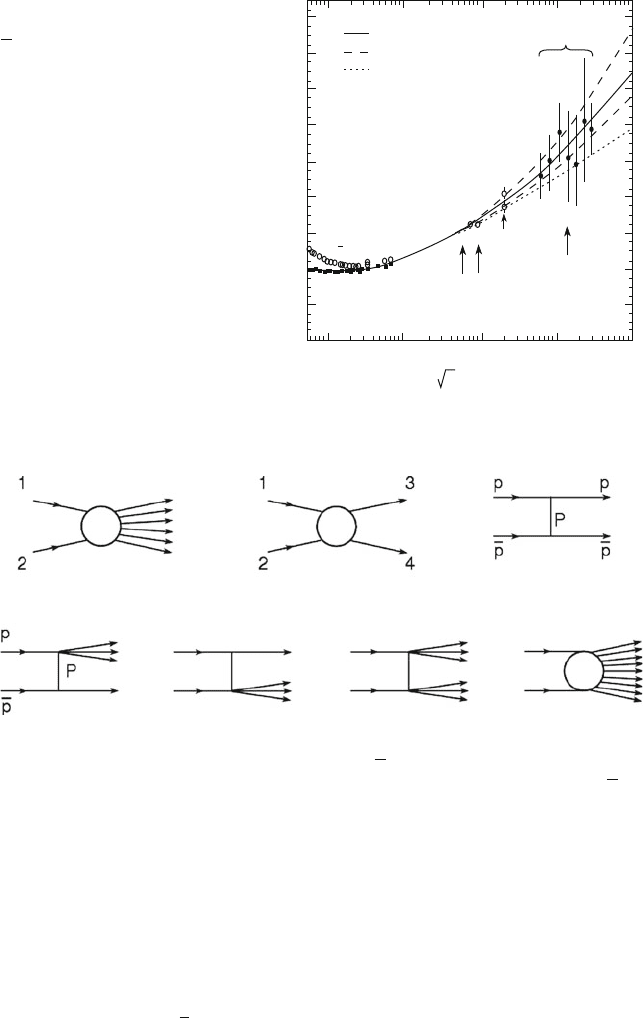
10.7 High Energy Hadron-Hadron Collisions 297
Fig. 10.19 Total
cross-section measurements
in
pp and pp collisions; data
include high energy cosmic
ray interactions
0
20
40
60
80
100
120
140
160
180
10 10
2
10
3
10
5
TEVATRON
LHC′
ISR
UA5
UA4
Cosmic ray
data
γ = 2.2 (best fit)
+ – 1σ
γ = 1.0
s (GeV)
σ
pp
σ
pp
σ
tot (mb)
10
4
a
de f g
bc
Fig. 10.20 Sketch of (a) inelastic and (b) two-body (if elastic, one has 1 D 3 and 2 D 4)
processes. A further subdivision, considered in detail for
pp collisions, is the (c) elastic collision
with a Pomeron P exchange; (d) single-diffractive on proton; (e) single-diffractive on
p;(f)
double-diffractive; (g) inelastic as in (a)
Before 1975, the experimental apparatuses used to analyze the production of
particles were very simple. Usually, they consisted of one or more layers of
scintillation counters with one or more Cherenkov counters to measure the incident
particle velocities and deduce their masses. Some experiments were also equipped
to cover the solid angle region near the beam pipe. The first detector which covered
almost the entire solid angle was the SFM (Split Field Magnet) at the CERN ISR.
The c.m. energy was
p
s ' 53 GeV. After 1975, larger equipment and detectors
were built, always covering almost the entire solid angle. The real “universal”
298 10 High Energy Interactions and the Dynamic Quark Model
detectors were born at the CERN SppS Collider (
p
s ' 540 GeV) with the UA1 and
UA2 experiments. The history continued at the Fermilab collider (
p
s ' 1,800 GeV)
with the Collider Detector Facility (CDF) and the D0 experiments. These detectors
(similar to those used at the e
C
e
colliders discussed in Chap. 9) operate effectively
in the c.m. system, and detect all secondary particles emitted in the full solid angle
with a series of concentric subdetectors. Starting from the interaction point, one
finds a tracking detector within a magnetic field, a time-of-flight system, an EM
calorimeter, a hadron calorimeter, and finally a muon detector.
To observe every hadronic interaction without setting any condition, a minimum
bias trigger requires that at least one charged track leave the interaction region.
More selective triggers may require a high-p
t
particle, a “jet” of particles, and so on.
The major result obtained in a hadron-hadron collider at high transverse mo-
mentum was discovered in 1983 regarding the W
˙
and Z
0
vector bosons (see
Problem 10.6) at the CERN Sp
pS, as described in Sect. 8.15. In the following,
we shall mostly focus on the ln s process and on some interpretative models.
10.8 Total and Elastic Cross-Sections at High Energy
Figure 10.19 shows a compilation of total proton-proton cross-sections for
p
s>
5 GeV. The cross-sections for the six charged hadrons with long lifetime (
˙
;K
˙
,
as well as p;
p) decrease with increasing energy, reach a minimum and then increase
with energy. For
pp and pp, the increase is of the type ln
2
s. Note that the argument
of a logarithm must be dimensionless: ln
2
s means ln
2
.s=s
0
/ with s
0
D 1 GeV
2
.The
cross-sections for antiparticle-proton
tot
.xp/, with x D
;K
; p, are larger than
those for particle-proton
tot
.xp/, with x D
C
;K
C
;p.
The difference D
tot
.xp/
tot
.xp/ decreases with increasing energy, in
agreement with the Pomeranchuk theorem which predicts that in the limit s !1,
tot
.xp/ D
tot
.xp/. This theorem can be derived from the hypothesis that the
number of available channels (i.e., the number of possible final states) increases
with energy; the total cross-section remains finite and that the cross-section for each
channel decreases asymptotically to zero with increasing energy. In this case, the
annihilation channels, possible for
xp and not for xp, are relatively few (in percent)
and at high energy, they have a negligible cross-section compared to that of all other
channels.
It is unclear why the total cross-sections increase with increasing energy. It
is likely due to either the increase of the gluon contribution (responsible for the
presence of “minijets”) or to the increase of diffractive-type phenomena.
10.8.1 Elastic Differential Cross-Sections
The elastic differential cross-section for a collision between two unpolarized
hadrons depends on the c.m. energy and on a variable which depends on the
