Borovik A. Shadows of the Truth: Metamathematics of Elementary Mathematics

Подождите немного. Документ загружается.

5.2 Dedekind-Peano axioms 45

So, let us look at axioms for arithmetic introduced by Richard

Dedekind (but commonly called Peano axioms) in the hope that

they provide some insight in the nature o f EHK’s and AB’s difﬁ-

culties.

5.2 Dedekind-Peano axio m s

Recall that the Dedekind-Peano axioms de scribe the properties of

natural numbers N in term s of a “successor” f unction S(n). There is

no canonical notation for the successor function, in various books

it is denoted s(n), σ(n), n

′

, or even n

, as in popular computer

languages C and C

Axiom 1 1 is a natural number.

Axiom 2 For every natural n umber n, S(n) is a natural number.

Axioms 1 and 2 deﬁne a unary representation of the n atural

numbers: the number 2 is is another name for S(1), and, in general,

any natural number n is

n−1

(1) = S(S(···S(1) ···)) (n − 1 times).

As we shall soon see, the next two axioms deserve to be treate d

separately; they deﬁne the properties of this repre sentation.

Axiom 3 For every natural number n other than 1, S(n) 6= 1. That

is, there is no natural number whose successor is 1.

Axiom 4 For all natural numbers m and n, if S(m) = S(n), then

m = n. That is, S is an injection.

The ﬁnal axiom (Axiom of Induction ) has a very different nature

and is best understood as a method of reasoning about all natural

numbers.

Axiom 5 If K is a set such that:

• 1 is in K, and

• for every natural number n, if n is in K, then S(n) is in K,

then K contains every natural number.

Thus, Ded ekind-Peano arithmetic is a formalisation of that very

counting by one that little EHK did, and addition is deﬁned in pre-

cisely the same way as EHK le arned to do it: by a recu r sion

m + 1 = S(m)

m + S(n) = S(m + n).

Commutativity of addition is a non-trivial theorem (although still

accessible to a beginner) . To force yo u to sympathize with poor little

EHK and to p oor little AB, I will pr ove it to you in Section 5.5.2.

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

46 5 Adding One by One

5.3 A brief digression: is 1 a number?

Having postponed more serio us work, we can spend a f ew minutes

discussing Axiom 1:

1 is a n a tu ral n umber.

Even this axiom is no t as self-evident as it app ears to be. In

many languages, including English, the word “num ber” can denote

some collection or ensemble of objects with the tacit understand-

ing that it contains at least a few, and in any case more than one,

objects. For example,

“A number of people feel that 1 is not a number”

makes sense and sugg ests that more than one per so n thinks that 1

is not a number. Such usage reﬂects an earlier stage of development

of the system of numerals in which 1 was not a number; numbers

were made o f ones, of basic units; but 1 is no t made of ones.

What is very important for the history of mathematics, it ap-

pears that, for similar r easons, 1 was not a number for ancient

Greek mathematicians, as evidenced in Euclid’s Elements: Euclid

carefully separated the use of the w ords “number” and “unit”.

And, as a digre ssion within digression, I want to mention the

issue of collective nouns—I shall discuss them again in later chap-

ters, so the present digression is not waste of time. The English

language has a peculiar tendency to form or ﬁn d a special word to

denote groups of particular animals. Fo r example, Englishmen say

a herd of cows,

a ﬂock of sheep,

a pack of dogs,

a school of ﬁ sh.

To illustrate how far things go, it will sufﬁce to men tion that ducks

on water form a paddli ng, but when in ﬂ ight they are a ﬂush. Some

nouns are obscure; f or example, I foun d in Wikipedia a sedge of

bitterns, but I did not even know what bitterns are. A dictionary

told m e that bittern was a familiar vypь—which puzzled me even

more because I thought that vypь was a rather solitary bird; see

Figure 5.1.

The in vention of collec tive nouns for g roups of people from var-

ious p rofessional groups is an (admittedly, fringe) genre of English

humor; to my taste,

a number of mathematicians

appears to be one of the more obviou s solutions.

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

5.4 How much mathematics can a child see at the level of basic counting? 47

Fig. 5. 1 . Bittern (Botaurus stellaris).

5.4 Ho w much mathematics can a child see at the

level of basic counting?

We postpone the promised systematic developm ent of the concept of

addition once more and will ﬁrst look at how much child can see at

the level of basic counting and the most pr imitive form of addition,

by adding one by one. Quite a lot, apparently, as conﬁrme d by a

striking testimony from Roy Stewart Roberts

On a large sheet of paper I made a triangle of numbers and addi-

tion signs as below. Down the right side I made a list of the results

of the additions. It was clear that this process could continu e as

long as I wanted an d my attention went to the vertical sequence

on the right.

. 0

1 1

2 + 2 4

3 + 3 + 3 9

4 + 4 + 4 + 4 16

5 + 5 + 5 + 5 + 5 25

6 + 6 + 6 + 6 + 6 + 6 36

7 + 7 + 7 + 7 + 7 + 7 + 7 49

. . .

It was clear that the numbers in the sequence increased more

rapidly as you went down so I formed the sequ ence of ﬁrst dif-

ferences. Of course I obtained the odd numbers. So I thought, “Is

this true in general? Does th e sequence continue always to gen-

erate the odd numbers no matter how far we go?” I also thought,

RSR tells about himself: “ As an adult I obtained a PhD in mathematics,

differential topology–group actions on manifolds and ﬁbre bundles, and

now am retired if mathematicians ever retire. My mother tongue is En-

glish and the above mathematics was all in Engl ish.” The episode took

place before he went to school.

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

48 5 Adding One by One

“Can I prove it?” and asked my father, who had a PhD in chem-

istry. He conﬁrmed that the odd numbers were indeed correct a nd

mentioned algebra. I wondered how can he know and ca n I prove

it? I think I thought in terms of a proof based on counters; I did not

know my addition ta bles and certain ly n ot my multiplication ta -

bles, and performed the additions by counting, mai nly in my head

but possibly also using my ﬁngers. I did not properly formulate

a proof b ased on counters until grown up, as I later h ad algebra

that made the result obvious an yway. A proof bas ed on counters is

quite easy and possibly I got near to it at the time.

Perhaps I did not continue thinking about the matter to the

point of constructing a proof because I became aware of the ques-

tion, “Even if I get a proof, how will I know the proof is correct?”

This question bothered me. I think I was aged four at the time,

coming up to ﬁ ve, just after the Second World War was ended.

Roy Roberts’s story mentions further interesting insights:

The point at the top of the trian gle denoted zero zeroes added to-

gether. The symbol “0” would not have been correct and I had a

little difﬁculty deciding what I should put at the top.

Evidently I understood zero. At some point, probably earlier

than the research, I had discovered that you can continue countin g

forever, using the usual representation of numbers if one ran out

of names.

Roy Roberts mentioned “a proof based on counters” for the for-

mula

1 + 3 + 5 + ··· + (2n + 1) = (n + 1)

(5.1)

(where, we have to remember, (n + 1)

means “n + 1 adde d with

itself n + 1 times”). He added an explanation:

In order to subtract a square number from the next in sequence,

think of a square array of counters for the larger and remove a

square array for the smaller, necessarily based in a corner. The re-

sult is an “L” s hape of counters with the two legs of the “L” of equal

length. This clearly generates the odd numbers but to see this just

repeat the above argument, remove from the “L” the smaller “L” in

sequence and the result is two separate counters, hence generat-

ing the odd numbers.

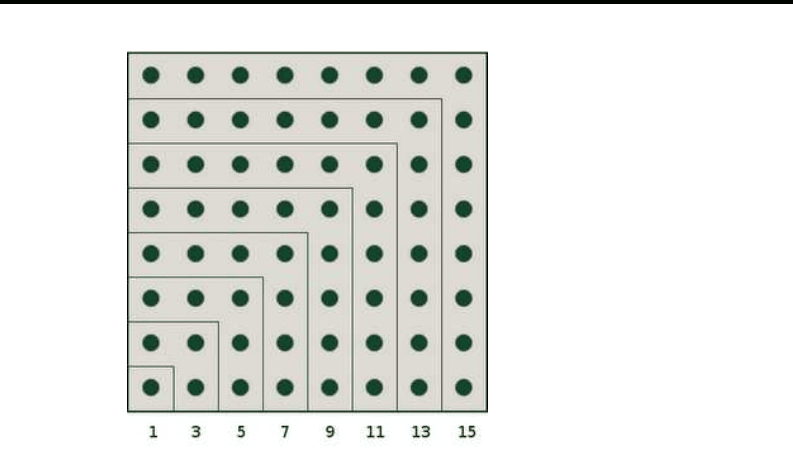
We can also easily see that this proof is an oral description of

the famous visual p r oof; see Figure 5.2. It is a pity that the picture

was not shown to 4 years old Roy.

It is wort noticing that a pro of of formula (5.1) by mathematical

induction is interesting for historic reasons: it appears to be a very

ﬁrst proof in print based on explicitly formulated principle of math-

ematical induction. It was done by Aug ustus De Morgan in 1838 in

a article in The Penny Cyclopedia of the Society for the Diffusio n of

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

5.4 How much mathematics can a child see at the level of basic counting? 49

Fig. 5.2. A visual proof of 1 + 3+5+ ···+ (2n + 1) = (n + 1)

. Image source:

[830].

Useful Knowledge [217]. I quote it at length; notice that De Morgan

uses the term successive induction:

INDUCTION ( Mathematics). The method of induction, in the

sense in which the word is used in natural philosophy, is not

known in pure mathematics. There certainly are instances in

which a general proposition is proved by a collection of the demon-

strations of different cases, which may remind the investigator of

the inductive process, or the collection of the general from the par-

ticular. Such instances however must not be taken as permanent,

for it usually happens that a general demonstration is discovered

as soon as attention is turned to the subject.

There is however one particular method of proceeding which

is extremely common in mathematical reasoning, a nd to whi ch we

propose to give the n ame of successive induction. It has the ma in

character of in d uction in physics, because it is really the collec-

tion of a general truth from a demonstration which implies the ex-

amination of every particular case; but i t differs from the process

of physics inasmuch as each case depends upon one which pre-

cedes. Substituting however demonstration for observation, the

mathematical process bears an analogy to the experimental one,

which, in our opinion, is a sufﬁcient justiﬁcation of the term ‘suc-

cessive induction.’ A coupl e of instances of the method will enable

the mathematical reader to recognise a mode of investigation with

which he is already familiar.

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

50 5 Adding One by One

Fig. 5.3. An informal des cri ption of mathematical induction can be illus-

trated by reference to the sequential effect of falling dominoes. Tipping

the ﬁrst domino: a still from the famous Guinness advert Tipping Point,

director Nicolai Fuglsig, 2007.

Example 1 .—The sum of any number of successive odd num-

bers, beginning from unity, is a sq uare number, namely, the square

of half the even number which follows I he last odd number. Let

this proposition be true in any one single instance; that is, n be-

ing some whole nu mber, let 1, 3, 5 up to 2n + 1 put together give

(n+1)

. Then the next odd number being 2n+3, th e sum of all the

odd numbers up to 2n + 3 will be (n + 1)

+ 2n + 3, or n

+ 4n + 4,

or (n + 2)

. But n + 2 is th e ha lf of the even number next following

2n + 3: consequently, if the proposition be true of any one set of

odd numbers, it i s true of one more. But it is true of the ﬁrst odd

number 1, for thi s is the square of half the even number next fol-

lowing. Consequently, bei ng true of 1, it is true of 1 + 3; being true

of 1 + 3, it is true of 1 + 3 + 5; being true of 1 + 3 + 5, it is true of

1 + 3 + 5 + 7, and so on, a d inﬁnitum.

5.5 Properties of addition

After all the delays and detour s we ﬁnally come to rigorous mathe-

matical exploration of addition.

I have already mentione d that there are several alternative

forms of notation for the successor function: S(n), s(n), σ(n), n

′

and

even n

. I shall use notation n

′

; as the reader will soon see, it is

very convenient—and natural—to write a symbol for the successor

function after the number that has to be incremented.

In this new n otation, the recursive rule for addition looks like

n + 1 = n

′

(5.2)

n + m

′

= (n + m)

′

. (5.3)

I will also use Axiom 5 in a more conventional form, which is

obviously equivalen t to the original on e.

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

5.5 Properties of additi on 51

Axiom 5 Assume that a certain statement about numbers is such

that:

• the statement is true for number 1 ( B asis of Inducti on);

• if the statement is true for a natural number n (Inducti ve

Assumption) then it is true for the next number n

′

(Inductive

Step).

Then the statement is true for all natural numbers.

I n ow prove two canonical proper tie s of add ition.

5.5.1 As sociativity of addition

Theorem 1. Assume that + is a binary operatio n which satisﬁes

conditio ns (5.2) and (5.3). Then + is associative, that is,

(a + b) + c = a + (b + c)

for all a, b, c.

Proof. The proof uses induction on c.

Basis of Indu c tion.

(a + b) + 1

by (5.2)

= (a + b)

′

by (5.3)

= a + b

′

by (5.2)

= a + (b + 1).

Inductive Assu mption:

(a + b) + c = a + (b + c).

Inductive Step.

(a + b) + c

′

by (5.3)

= ((a + b) + c)

′

by inductive

assumption

= (a + (b + c))

′

by (5.3)

= a + (b + c)

′

by (5.3)

= a + (b + c

′



SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

52 5 Adding One by One

5.5.2 Commutativity of addition

We start with a very special, but crucially imp ortant case.

Theorem 2. Assume that + is a binary operatio n which satisﬁes

conditio ns (5.2) and (5.3). Then

1 + a = a + 1

for all a.

Proof. We shall prove the theorem by induction on a.

Basis of Indu c tion.

1 + 1 = 1 + 1.

There is nothing to prove here.

Inductive Assu mption:

1 + a = a + 1.

Inductive Step.

1 + a

′

by (5.3)

= (1 + a)

′

by inductive

assumption

= (a + 1)

′

by (5.2)

= (a

′

)

′

by (5.2)

= a

′

+ 1.



Theorem 3. Assume that + is a binary operatio n which satisﬁes

conditio ns (5.2) and (5.3). Then + is commuta ti ve, that is,

a + b = b + a

for all a and b.

Proof. We pro ve the theorem by ind uction on b.

Basis of Indu c tion: Theorem 2.

Inductive Assu mption:

a + b = b + a.

Inductive Step.

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

5.6 Dark clouds 53

a + b

′

by (5.3)

= (a + b)

′

by inductive

assumption

= (b + a)

′

by (5.2)

= (b + a) + 1

by Theorem 1

= b + (a + 1)

by Theorem 2

= b + (1 + a)

by Theorem 1

= (b + 1) + a

by (5.2)

= b

′

+ a.



5.6 Dar k clouds

Notice that I was careful to formulate Theorems 1–3 in the most

cautious way, by emp hasizing their conditional nature:

if + is a binary operation which satisﬁes conditions (5.2) and (5.3)

then . . .

The reason for my restraint is that writing down conditions (5.2)

and (5.3) does not mean they deﬁne a functio n.

Another problem is that if you look at the proofs of Theorems 1–

3, you notice that they do not refer to Axioms 3 and 4 and are based

entirely on the Induction Axiom, Axiom 5. Therefore if we can ex-

hibit a “toy version” of a system of natural n umbers where we have

a distinguished e lement 1, and the successor function S, and the

Induction Axiom, but have no Axioms 3 and 4, we shall still be able

to deﬁne addition by conditions (5.2) and (5.3), and pe rhaps some

other functions.

David Pierce [73] suggests that w e take for such a “toy model” a

system of residue s Z/nZ modulo n, w ith re sidue 1 in the role of the

distinguished element, and with a succe ssor function

x 7→ x + 1 mod n.

David Pierce make s an incisive comment:

Indeed, if one thin ks that the recursive deﬁnitions of addition and

multiplica tion—

n + 0 = n,

n + (k + 1) = (n + k) + 1;

n · 0 = 0,

n · (k + 1) = n · k + n

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

54 5 Adding One by One

—are obviously justiﬁed by ind uction alone, then one may think

the same for exponentiation, with

= 1

k+1

= n

· n.

However, while a ddition and multiplication are well-deﬁned on

Z/nZ (which admits indu ction), exponentiation is not.

Indeed , the recursive d eﬁnition of exponentiation fails in Z/3Z:

n n

× n n

2 1 2 1 2

(so n

× n is not equal n

, what is disappointing).

But the recursive d eﬁnition of exponentiation holds in Z/6Z:

n n

1 1 1 1 1 1 1

2 4 2 4 2 4 2

3 3 3 3 3 3 3

4 4 4 4 4 4 4

5 1 5 1 5 1 5

6 6 6 6 6 6 6

The former is an exception rather than rule, as clariﬁed by the

following theore m.

Theorem 4 (Don Zagier [93]). On Z/nZ, the recursive deﬁnition

of exponentiation

= 1

k+1

= n

· n.

is valid if and only if

n ∈ {0, 1, 2, 6, 42, 1806}.

The desired n are such that

n+1

≡ x (mod n);

such n were f ound by John Dyer-Bennet [10] and Don Zagier [93].

Indeed the function known in mo dular arithmetic as exponenti-

ation is a map

(Z/nZ)

∗

× Z/φ(n)Z → Z/nZ

(x, y) 7→ x

where (Z/nZ)

∗

, as usual, denote s the group of invertible elements

of the residue ring Z/nZ. Its order is φ(n) for Euler’s function φ,

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK