Borovik A. Shadows of the Truth: Metamathematics of Elementary Mathematics
Подождите немного. Документ загружается.


9.4 Some practical issues 105
changes in school syllabi, the so-called “widening participation
agenda”, etc.
I argue that the intrinsic methodological link with re search
makes teaching of m athematics at the university lev el different
from teaching many other univer sity disciplines. Of course, it also
makes university teaching very different from secondary school
teaching. I believe that for that reason university level mathemat-
ics teaching deserves some special treatment in educational re-
search.
SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19
c
ALEXANDRE V. BOROVIK

10
Carrying: Cindere lla of Arithmetic
10.1 Palindromic decimals and palindromic
polynomials
My next case study is based on conversations with an 8 year old
boy, DW, in May 2007.
DW’s parents sent me a file of DW’s book. It included the follow-
ing paragraph, reproduced he re verbatim:
I wrote to DW:
Dear D,
Indeed, there is something weird. I believe you have figured
out that
107
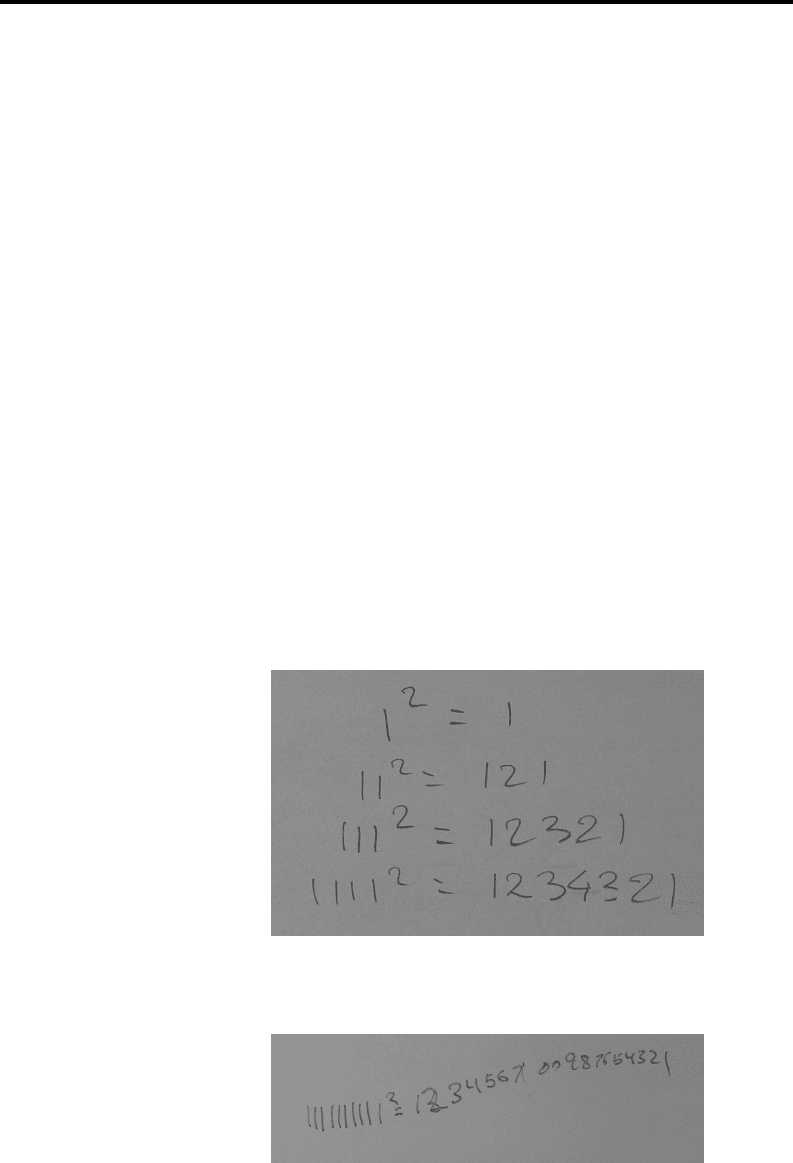
108 10 Ca rrying: Cinderella of Arithmetic
1 × 1 = 1
11 × 11 = 121
111 × 111 = 12321
1111 × 1111 = 1234321
11111 × 11111 = 123454321
111111 × 111111 = 12345654321
1111111 × 1111111 = 1234567654321
11111111 × 11111111 = 123456787654321
111111111 × 111111111 = 12345678987654321
There is a wonderful p alindromic pattern in the results. But math-
ematics is interested not so much i n beautiful patterns but in the
reasons why the patterns cann ot be extended without loss of their
beauty. In our case, the pattern breaks at the next step (judging
by your book, you have already noticed that):
1111111111 × 1111111111 = 1234567900987654321
The result is no longer symmetric. Why? What is the difference
from the previous 9 squares? Can you give any suggestions?
I had some brief e-mail exchanges with DW which suggested
that he might have an explanation, but could not clearly express
himself. Our discussion continued when he visited me (with h is
mother) in Manchester on 8 May 2007.
I wrote on the whiteboard in my office (this is a ph otograph of
actual writing on the board):
and asked DW whether the symmetric pattern of results continued
indefinitely. DW instantly answered “No” and also instantly wrote
on the board, app arently from memory:
SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19
c
ALEXANDRE V. BOROVIK
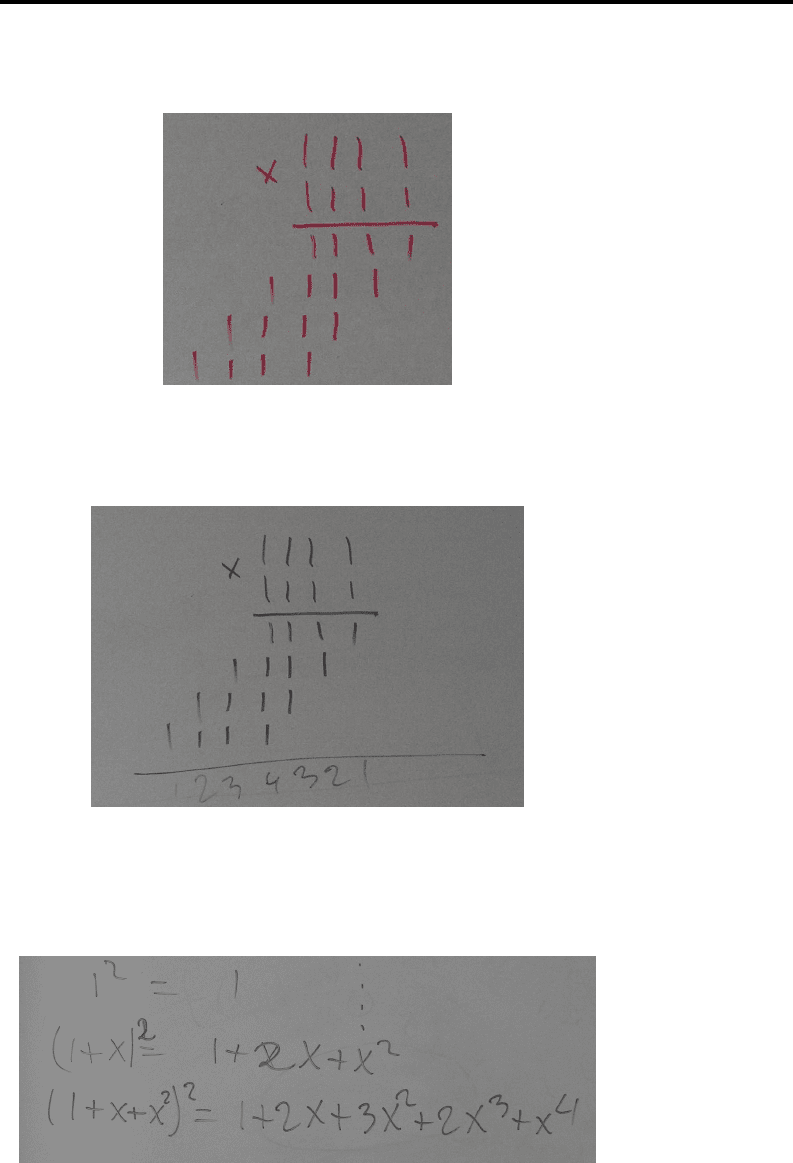
10.1 Palindromic decimals and palindromic polynomials 109
“Good”—said I—but le t us try to figure out why this is happen -
ing”, and wrote on the board:
“Yes”—said DW—“this is column multiplication”.
“And wh at are the sums of columns’?”
“1, 2, 3, 4, 3, 2, 1”—dictated DW to me, and I have written down
the result:
“Will the symmetric p attern continue indefinitely?”—asked I .
“No”—was DW’s answer—“when ther e are 10 1’s in a column, 1
is added on the left and there is no symmetry.”
“Yes!”—said I—carries break the symmetry. But let us look at
another examp le”—and I wrote:
SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19
c
ALEXANDRE V. BOROVIK

110 10 Ca rrying: Cinderella of Arithmetic
DW was intrigued and made a couple of experiments (and it
appeared from his behavior that he was using mostly mental arith-
metic, writing down the result, ter m by term, w ith pauses):
and said with obvious enthusiasm: “Yes, it is the same pattern!”
“Wonderful”—answe r ed I—“let us see why this is hap pening.
I’ll give you a hint: m ultiplication of polynomials can be written as
column multiplication”, and started to write:
DW did not let me finish, grabbed the marker from my hand
and insisted on doing it himself :
He stopped after he barely started the second line and said very
firmly: “Yes, it is like with numbers”.
SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19
c
ALEXANDRE V. BOROVIK

10.2 DW: a discussion 111
“Well”—said I—“but will the pattern break down or will it con-
tinue forever?”
That was the first time when DW fell in deep thought (and I
was a bit uncomfortable about the d egree of his c oncentration and
retraction fro m the real world). This was also the first time when
his response was not instant—perhaps, a wh ole 20 seconds passed
in silence. Then he suddenly smiled happily and answered: “No, it
will not break down! ”
“Why?”—inquired I.
“Because when you add po lynomials, the coefficients just add
up, there are no carries .”
At that point I decided to stop the session on the pretext that
it was late and the boy was perhaps tired, but, to ro und up the
discussion, made a general commen t:
“You know, in mathematics polynomials are sometimes used to
explain what is happenin g with numbers”.
The last word, however, belonged to DW:
“Yes, 10 is x.”
10.2 DW: a discussion
DW is a classical example of what is usually called a “mathemati-
cally able child” (althou gh I prefer to avoid this much compromised
expression and say instead “mathem atically inclined child”). He
mastered, more or less on his own, some mathematical r outines—
multiplication of decimals and polynomials—which are normally
taught to children at a mu ch later age. He also showed instinctive
interest in d etecting beau tiful patterns in the behavior of n umbers,
and, which is even more important, in the limits of applicability of
patterns, in their breaking points.
DW understands what is generalization and, m oreover, loves
making quick, I would say recklessly quick generalizations. Vadim
Krutetsky [796] lists this trait among characteristic traits of “math-
ematically able” children: very frequently, they are children , who,
after solving just one problem, already kn ow how to solve a ny prob-
lem of the same type.
But let us return to our principal theme: the hidden structures
of elementary m athematics. In our conversation, DW was shown —
I emphasize, for the first time in his life—a beautiful but hidden
connection between dec im als and polynomials—and was able to see
it!
In our little e xercise, DW advanced (a tiny step) in conceptual
understanding of mathematics: he had seen an example of how
one mathematical structure (polynomials) may hide inside another
mathematical structure (decimals).
SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19
c
ALEXANDRE V. BOROVIK

112 10 Ca rrying: Cinderella of Arithmetic
My final comment is that although DW made a small, but im-
portant step towards deeper understanding of mathematics, this
step is no t necessarily visible in the usual mathematics education
framework. It is un likely that a school assignment will detect him
making this small step. Proce durally, in this small exe rcise DW
learned next to nothing—he had multiplied numbers and polyno-
mials before, and he will multiply them with the same speed after-
wards.
One sho uld not conclude, however, that the “procedu r al” aspect
of mathem atics is o f no importance. DW’s ability to do this tiny bit
of “conceptual” mathematics wou ld be impossible without him mas-
tering the standard routines (in this case, column multiplication of
decimals and addition and multiplication of polynomials).
10.3 Decimals and polynomials: an epiphany
DW’s words “10 is x” is a f ormulation of analogy between decimals
and polynomials which is not frequently emphasized in schools bu t,
when discovered by children on their own, is experienced as an
epiphany. This expr ession is taken from another childhood story,
by LW.
1
When I was in the fourth grade (ab out 9 years old) , we learned long
division. I had enormous difficulty learning the method, though I
could divide 3 and 4 digit numbers by 1–2 digit numbers in my
head. I don’t recall exactly how I did the divisions in my head,
though I susp ect that the method was similar to long division. I
recall that it was broadly based on “seeing how much I needed to
add to the result to move on.” However, I couldn’t seem to remem-
ber long division, despite being able to follow a list of instructions
on homework. My homework on long division took hours to finish.
I think the iss ue was that my teacher and parents never explained
why long division a ctu ally worked, so it seemed like a disconnected
list of steps that ha d little relation to one a nother. On a quiz, my
teacher thought I had cheated, since I had written no work on any
of the problems.
I only became able to do long division in high school when I
learned how to do long division with polynomials. At that time, the
teacher went to great pains to explain why it worked. While doing
a homework, I had an epip hany: long d ivision for polynomials was
a close cousin of long division for numbers. Suddenly I could d o
long division of numbers.
I now take pains when teaching calculus to try and explain
why formulas are true whenever possible. This has lead to mixed
1
LW was 9 years at the time of his story, he is male, learned mathemat-
ics in American English (his native tongue), currently is a second year
student in a PhD program in pure mathematics.
SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19
c
ALEXANDRE V. BOROVIK

10.4 Carrying: Cinderella of arithmetic 113
reactions on my evaluations, with some students saying that they
enjoy knowing why the formulas are true and others saying that
they have enough trouble learning formulas in the first place with-
out having to also learn why they’re true. For me, the two are
deeply connected. If I don’t know why something is true (at least
in broad outline), I fi nd it significantly harder to remember.
As we shall see in the next section, LW had eve ry reason indeed
to ask “Why?”—de cimals is an immensely rich structure.
Also, LW’s story is an evidence in sup port of another observa-
tion made by Krutetskii [796]: “mathematically inclined children”
may appear to be slow because they are frequently trying to solve
a more general problem than the one given, and they understand
the underlying reasons fo r a rule they are told to app ly unque stion-
ingly.
10.4 Ca rrying: Cinderella of arithmetic
The deceptive simplicity of elementary school arithmetic is espe-
cially transparent when we take a closer look at carries in the ad-
dition of decimals.
10.4.1 Cohom ology
In Molière’s play Le Bourgeois Gentilhomme, Monsieur Jourdain
was surprised to learn that he had been speaking prose all his life:
PHILOSOPHY MASTER: Is it verse that you wish to write her?
MONSIEUR JOURDAIN: No, no. No verse.
PHILOSOPHY MASTER: Do you want only prose?
MONSIEUR JOURDAIN: No, I don’t want either prose or verse.
PHILOSOPHY MASTER: It must be one or the other.
MONSIEUR JOURDAIN: Why?
PHILOSOPHY MASTER: Because, sir, there is no other way to ex-
press oneself than wi th p rose or verse.
MONSIEUR JOURDAIN: There is nothing but prose or verse?
PHILOSOPHY MASTER: N o, sir, everything that is not p rose is
verse, and everything that is not verse is prose.
MONSIEUR JOURDAIN: And when one speaks, what is that then?
PHILOSOPHY MASTER: Prose.
MONSIEUR JOURDAIN: What! When I s ay, “Nicole, bring me my
slippers, and give me my nightcap," that’s prose?
PHILOSOPHY MASTER: Yes, Sir.
MONSIEUR JOURDAIN: B y my faith! For more than forty years I
have been speaking prose without knowing anything about it, and
I am much obliged to you for having taught me that.
SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19
c
ALEXANDRE V. BOROVIK

114 10 Ca rrying: Cinderella of Arithmetic
I was recently reminded that, starting from my ele mentary
school and then all m y life, I was calculating 2-cocycles.
Indeed , a carry in elementary arithmetic, a digit that is trans-
ferred from one column of digits to another column of more signifi-
cant digits during addition of two decimals, is defined by the rule
c(a, b) =
1 if a + b > 9
0 otherwise
.
One can easily check that this is a 2-cocycle from Z/10Z to Z and is
responsible for the extension of add itive groups
0 −→ 10Z −→ Z −→ Z/10Z −→ 0.
DW discovered (without knowing the words “2-cocycle” and “coho-
mology”) that carry is doing what cocycles frequently do: they are
responsible for breaking symmetry.
Carry is dif ficult in itself, but psychological diffi culties in its
computation are aggravated by lower level cognitive hindrances,
as a brief comment from Alex Cook
2
illustrates:
When doing basic mental addition (eg of exam scores) I find it
harder to do
A: 23 + 8 =
than
B: 28 + 3 =
Ditto for other sums when the second number is between 6 and 9.
Not sure if this has plagued me since childhood or n ot.
Children may develop their own idiosyncr atic procedures for
handling carries and stick to them for all their lives. This is a c om-
ment from Toby Howard
3
:
Whenever I add numbers, I partially subtract from the next mul-
tiple of ten. Example: for 7 + 8, I would think “7 needs 3 to make
10, so we have 5 left over, to add to the 10, so 10 + 5 = 15”. I seem
to have started this only in my teens.
And, as Logan Zoellner
4
reminded us, the problems start with
the ver y basics: concep ts of decimal place and decimal point:
I remember having d ifficulty grasping multiplication and long di-
vision with decimals. The principle of “move the decimal over and
2
ARC is male, British, was raised in Scotland, has a PhD in mathemati-
cal statistics, teaches statistics in an university.
3
TB is male, British, teaches computer science at an university.
4
LZ is male, American, university graduate, works as a mathematicia n.
SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19
c
ALEXANDRE V. BOROVIK
