Borovik A. Shadows of the Truth: Metamathematics of Elementary Mathematics

Подождите немного. Документ загружается.

Pedagogical Intermission:

Didactic Transformation

In Chapter 8, we had a roller coaster ride from exceptionally ele-

mentary to highly abstract mathematics. Let us take a short break,

to pause and r eﬂect.

I wish to d evote a few p ages to a discussion of the structure of

this book. Have you no ticed that I started with multiplication of

natural numbers and only then moved to addition? This is not the

natural logical or der for the two topics. I deviated from the natural

logic of development of mathematical theory for a simple reason:

for me, it m ade pedagogical sense to postpone the app lication of

severe rigor and the axiomatic method to later chapters.

The choice of the structure of the lecture course

which preceded

this book—and that determined the structure of the book—was

a quite explicit and deliberate decision. I spent at least an hour

thinking about it (wh ile slowly walking up a winding dusty road

through olive gr oves on the hills above ¸Sirince in Asia Minor). I

would be delighted to have comments from my readers: do they

agree that it was right choice?

Notice that in this chapter I will discuss mostly the issue of uni-

versity mathematics education. Even if the topic of the book is ele-

mentary mathematics, it is discussed at a university mathematics

level.

9.1 Didactic transfo rmation

It is time to introdu ce some deﬁnitions.

A remarkably c ompact formulation of what makes mathemat-

ics education so special can be found in a paper by a prominent

mathematician Hyman Bass [604]:

Upon his retirement in 1990 as president of the International

Commission on Mathematical Instruction, Jean-Pierre Kahane

In the Nesin Mathemati cs Village, ¸Sirince, Turkey.

96 9 Pedagogical Intermission:Di dactic Transformation

Fig. 9.1. Guido Reni. A fragment of The Rape of Helena, 1631. Musée du

Louvre. Source: Wikipedia Commons. Public domain.

described the connection between mathematics and mathematics

education in the following terms:

• In no other living science is the part of presentati on, of the

transformation of discip linary knowledge to knowledge as it

is to be taught (transformation didactique) so important at a

research level.

• In no other discipline, however, is the distance between the

taught and the new so large.

• In no other science has teaching and lea rning such s ocial im-

portance.

• In no other science is there s uch an old tradition of scienti sts’

commitment to educational questions.

The concept of didactic transformation is fairly old and can be

traced back to Auguste Comte [109, preface]:

A d iscourse, then, which is in the full sense didactic, ought to

differ essentially from one [that is] simply logical, in which the

thinker freely follows his own course, paying no attention to the

natural conditions of all communication. [. . . ] On the other hand,

this trans f ormation for the purposes of teaching is only practicable

where the doctrines a re sufﬁciently worked out for us to be able to

distinctly compare the different methods of expanding them as a

whole and to easily foresee the objections which they will naturally

elicit.

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

9.1 Didactic transformation 97

Howeve r, a GOOGLE SCHOLAR search shows that the concept

is used in the (English language) literature on mathematics edu -

cation less widely than one wou ld anticipate. In French literature,

there is a concep t of transpos ition didactique; the term has been

devised by Yves Chevallard [627] and has become a mainstream

element of the French mathematics education theory. I prefer the

original term “didactic transformation” as coined by Comte; the

word “transposition” invites for a narrow understanding of the con-

cept as mere selection, adap tation and re-ordering of contents to be

taught. The word “transformation” has a wider meaning, and, as

this chapter will show, is more suitable.

We have to rem ember that even a simple change in order of ex-

position could have dramatic effects and u sually requires a serious

rethinking of the underlying logical development of the material.

Here is an example suggested by Roy Stewart Roberts:

I suggest that a course in calcu lus and analysis should deﬁne the

logarithm function by the usual integral—a simple substitution

will give a proof that

ln xy − ln x = ln y.

This depends on having a theory of integration that enables th e in-

tegration of continuous functions, but we would want this anyway.

Then deﬁne

= exp(y ln x),

where of course exp is deﬁned to be the inverse function to ln.

To develop the theory based on the extension of a

from x ratio-

nal to x real woul d need some subtle analysis, possibly including

uniform continuity. I therefore favour the deﬁn ition of ln as an in-

tegral.

The reader would perhaps agree that a practical realization

of this interesting proposal requires some careful mathematical

work—and this chapter contains much more dramatic examples of

possible alternative approaches to calculus.

We have to accept that, in mathematics, didactic transformation

is indeed a form of mathematical practice. Moreover, it is in a sense

applied research since it is aimed at a speciﬁc application of math-

ematics: teaching. It remains mostly u npublished, underrated and

ignored because it is frequently conﬁned to early stages of cou rse

development or to e phemera of classroom practice.

Didactic transformation could, and shou ld be informed by ad-

vice from researchers in education and cognitive psychologists—

but methodologically it remains a part of hardcore mathematics.

Indeed , returning to Comte’s words:

. . . the doctrines are sufﬁciently worked out for us to be able to

distinctly compare the different methods of expanding them . . .

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

98 9 Pedagogical Intermission:Di dactic Transformation

we see that, in the context of unive r sity level mathematics teach-

ing, the expressions “work out” and “expand” refer to purely mathe-

matical activities: essentially, they mean “to prove, or check math-

ematically”. The situation with the words “distinctly compare” is

even more interesting: here we see in action the reﬂexive power

of mathematics as a precise and ﬂexible tool for the study of the

structure and func tion of mathematics itself.

Unfortunately, the principles of did actic transformation are fre-

quently n eglected in the mainstream mass mathematics instruc-

tion. Hans Freude nthal even coined the expression “anti-didactic

inversion” [646], to describe the regrettable situation when purely

procedural aspects of mathematics dominate the teaching at the

expense of explaining where these procedures came from and how

they are justiﬁed.

No mathematical idea has ever been published i n the way it was

discovered. Techniques have been developed and a re us ed, if a

problem has been solved, to tu rn the solution procedure ups ide

down, or if it is a larger complex of statements and theories, to turn

deﬁnitions into propositions, and propositions into deﬁnitions, the

hot invention into icy beauty. This then if if has affected teaching

matter, is the dida ctical inversion . . .

[However] one should recognise that the young learner is enti-

tled to recapitulate in a fashion the learning process of mankind.

Not in the trivial abridged versi on, but equally we cannot require

the new generation to start just at the point where their predeces-

sors left off. [646]

But I would rather avoid criticism. Instead, I wish to turn to

a case study. Its choice is motivated mostly by references to the

concepts of convergence and limit in the later chapters of this book.

9.2 C ontinuity, limit, derivatives

Few topics in under graduate education gene rate more controv ersy

than the classical epsilon-de lta approach to limits and continuity. I

quote Raphael Núnez [360, p. 179]:

Formal deﬁnitions and axioms in math emati cs are themselves cre-

ated by human ideas [. . . ] and th ey only capture very limited as-

pects of the richness of mathematical ideas. Moreover, deﬁnitions

and axioms often neither formalize nor generalize human every-

day concepts. A clear example is provided by the modern deﬁni-

tions of limits and contin uity, which were coined after the work

by Cau chy, Weierstrass, Dedekind, and others in the 19th cen-

tury. These deﬁnitions are at odds with the inferential organiza-

tion of natural continuity provided by cognitive mechanisms such

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

9.3 Continuity, limit, derivatives:the Zoo of alternative approaches 99

as ﬁctive and metaphorical motion. Anyone who has taught cal-

culus to new students can tell how counter-intuitive and hard to

understand the epsilon-delta deﬁnitions of limits and continuity

are (and this is an extremely well-documented fact in the math-

ematics education literature). The reason is (cognitively) simple.

Static epsilon-delta formalisms neither formalize nor generalize

the rich human dynamic concepts underlying continuity and the

“approaching” the location.

This thesis is fully developed in a boo k by Lakoff and Núnez

(2000) and is very representative of a school of thought in mathe-

matics education largely informed by neuro physiological research.

The “motion ” metaphor for a limit has its drawbacks and can be

confusing for a child. Here is a story from Azadeh Neman:

As for the limits, we were told to imagine an an imal getting closer

to point on the plane but not really arriving a t it. This is a very

poor description and gave me many years of unnecessary pain

while deal ing with limits. The thing is this animal might actually

decompose itself into ma ny different a nimals who have nothing to

do with the ﬁrst one and whoever acts more dramatical ly close to

a certain point will guide the limit close to that point.

Moreove r, a striking feature of Nunéz’s thesis (and the debate

on the role of the concept of limit in mathematics education in gen-

eral) is that it ignores an impressive variety of alternative treat-

ments of calculus available in the (research) mathematical litera-

ture, some of them being remarkably intuitive and e lementary.

9.3 C ontinuity, limit, derivatives:

the Zoo of alternative approaches

o-MINIMAL STRUCTURES. We shall start our excursion by visit-

ing a well established area of research on the boundary of real

analysis and mathematical logic—the so- called theory of o-minimal

structures—where all (deﬁnable) function s of a single variable hap-

pen to be piecewise mon otone and take all intermediate values. In

naive terms, these are functions whose graphs can be drawn with a

pencil, with the concept “can be drawn” be ing made explicit and rig-

orous [89]. Historically, the theory of o-minimal structures is a di-

rect descendant of Euclid’s Elements—it originates in Tarski’s work

on a d ecision procedure for Euclidean geometry [88].

NON-STANDARD ANALYSIS, APRÈS ROBINSON. There is another

approach, due to the famous logician Abraham Robinson [80],

AN is female, Iranian, learned mathematics in Persian and later in En-

glish; at the time of this episode she was 15 and taught in Persian. AN

holds a PhD and is a postdoctoral researcher in mathematics.

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

100 9 Pedagogical Intermission:Di dactic Transformation

which places inﬁnitesimals (quantities and variables which are big-

ger than zero but smaller than any positive real number), purged

from calculus in 19th century, back at the core of the subject. So far,

this approach has made only relatively modest inroads into main-

stream teaching; see Keisler [40, 41, 43, 44]. Even at that subtle

point, I can quote a childho od testimony; it comes from Herbert

Gangl

When the teacher had introduced the notion of “nested intervals”

to prove that there always must lie one number and only one, I had

to sus p end my disbelief quite a bit—why couldn’t there be more

inside that limit? At the time I could imagine a kind of “cloud”

around such a limit point (maybe not necessarily embedded in the

real line) which still contains many more p oi nts in the limit, al-

though I couldn’t formulate it in any way.

Later on this “disbeli ef” was sort of redeemed when I was con-

fronted with inﬁ nitesimals, but my problem here (or at least one of

them) was that I had not understood the notion of continuity as we

are taught nowadays. (Later I discovered K ei sler’s book http://

www.math.wisc.edu/~keisler/calc.html

and found it very

intuitive.)

Eventually I adopted/accepted the “theorem” (about a u nique

number), but felt for quite some time th at I had taken a “leap of

faith” here.

I suppos e that this must have been around the age of 10–12,

it was taught to me in my mother tongue ( German), the notion is

“Intervallschachtelung”.

NON-STANDARD ANALYSIS, APRÈS NELSON. I nternal set theory

proposed by Nelson [69, 70] blurs the diffe rence between ﬁnite and

inﬁnite in a very simple, effective and controlled way. A brilliant lit-

tle book Nonstan dard Analysis by Alain Robert [ 79] demonstrates

the didactic power of this approach. The Introduction to the book

starts with a quote from Eule r:

Since L. Euler was among the most inspired users of inﬁnitesi-

mals, let him have the ﬁrst word . . .

Here is how he deduces the expansion of the cosine function in

his book [E] (Caput VII, Section V 133.). He starts from the Moivre

formula

cos nz =

[(cos z + i sin z)

+ (cos z − i sin z)

]

= cos

z −

n(n − 1)

1 · 2

cos

n−2

z sin

n(n − 1)(n − 2)(n − 3)

1 · 2 · 3 · 4

cos

n−4

z sin

z + ···

HG is male, German, has a PhD in mathematics, teaches in a British

university.

H. Jerome Keisler [43].

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

9.3 Continuity, limit, derivatives:the Zoo of alternative approaches 101

and writes (loc. cit., p. 141)

sit arcus z inﬁnite parvus; erit cos ·z = 1, sin ·z = z; sit

autem n numerus inﬁnite magnus, ut sit arcus nz ﬁnitae

magnitudinis, puta nz = v

cos ·v = 1 − v

/2! + v

/4!—etc.

In the context of Robert’s book, this argument makes pe rfect sense.

SYNTHETIC DIFFERENTIAL GEOMETRY. My correspondent Freder-

ick Ross has brought my attention to yet another

[. . . ] approach eschewing ǫs and δs for calculus called synthetic

differential geometry (due, like so much, to Lawvere). It is distinct

from Robin son’s approach in kind of an in teresting way. Robin-

son’s approach is via set theory. Synthetic di fferential geometry

wanders in via intuitionist logic via the obs ervation that

¬(¬(dx = 0)),

says th at one could construct a structure wherein there are num-

bers which could be equal to zero, but cannot be proven to be so,

thus leaving enough room to play in the cracks. T his is [. . . ] an in-

teresting way to do topology which divests it of much of its point-

set metaphor—which makes it particularly nice for computer sci-

ence purposes where that metaphor is so much baggage attached

to an otherwise essential tool.

The interested reader can ﬁnd a comp rehensive exposition of

synthetic differential geometry in Anders Kock [51].

CALCULUS IN O-NOTATION, APRÈS KNUTH. Next, there is a lec-

ture cour se by Do nald Knuth on calculus in O-notation, taught by

Knuth for may years and e xceptionally well polished pedagogically.

It is available from Knuth’s website and is partially published in

[24].

Donald Knuth’s approach to calculus via o-notation leads, ho w-

ever, to a different range of difﬁculties. A testimony from Mikhail

Katz:

I was studying at the FeMeSha no. 18 in Moscow around 1973. I re-

call being comfortable with the deﬁnition of derivative as a limit.

On the other hand, the alternative deﬁnition that the instructor

One has to know the cult status of Donald Knuth in the mathemat-

ical and computer science communities to fully appreciate his inﬂu-

ence: when I placed the text of his letter about teaching undergraduate

calculus [47] on my blog http://micromath.wordpress.com/2008/

04/14/donald-knuth-calculus-via-o-notation/, the post got

25,000 hits in 24 hours.

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

102 9 Pedagogical Intermission:Di dactic Transformation

provided caused me no end of a nxiety. Namely, he said the deriva-

tive is a number D such that

f(x) = f(a) + D(x − a) + o(x − a).

As you correctly point out, it takes a consi d erable amount of math-

ematical training to f ormulate precisely what the problem was.

The problem was that the deﬁnition says absolutely nothing about

how one could ﬁnd su ch a “o()”, or how to go about simultaneously

(in what sequence?) ﬁnding D an d “o()”. In retrospect, wh at I must

have been bothered b y is the non-cons tru ctive nature of this deﬁ-

nition.

Actually I am currently writing a text on cons tructivism, and

it could be that even after all these years I would still be unable to

identify the source of the anxiety were it not for the fact of having

understood constructivism better recently.

It is a timely reminder: didactic transformation is necessarily a

very subtle balancing act.

UNIFORM LIPSCHITZ BOUNDS. There is also a very promising ap-

proach to calculus based on eliminating the concept of a limit and

replacing it by uniform Lipschitz bounds [56, 60]. It is close in its

spirit to Knuth’s calculus in O-notation but differ s in some impor-

tant aspects and notation. For examp le, the deﬁnition of derivative

′

(a) of the function y = f (x) at point x = a become s

|f(x) − f (a) − f

′

(a)(x − a)| 6 K(x − a)

;

for a non-mathematician, it suf ﬁces to notice that the notorious

epsilons and deltas are not present in the formula. The “rich hu-

man dy namic concepts underlying continuity” so loved by N únez

have also go ne, having been replaced by a closely re lated—but

different—concept, that of approximation.

This d eﬁnition can be applied only to a narr ower class of func-

tions than the one usually called differentiable. It is natural to call

a function f deﬁned on a real segment [A, B] uniformly Lips chitz

differenti able on [A, B] if for some constant K

|f(x) − f (a) − f

′

(a)(x − a)| 6 K(x − a)

Howeve r, the class of uniformly Lipschitz diff erentiable fun ctions

sufﬁces for m ost engineering applications and is open to a rigorous

and didactically efﬁcient treatment in teaching.

The uniform bounds approach allows to introduce yet another

simpliﬁcation: at an entry level, differentiation can be introduced

as a mere factoring. I borrowed the following example from Michael

Livshits [56]—the derivative of the function y =

√

x can be found

by a simple manipulation from the toolbox of high school algebra.

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

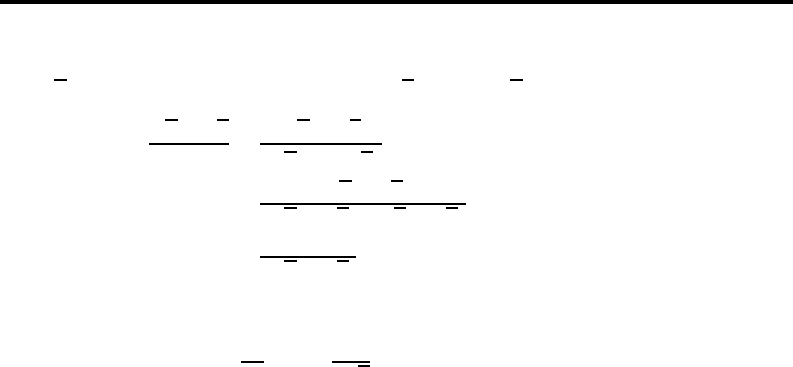
9.4 Some practical issues 103

We start with computing the slope o f the secant line to the curve

y =

√

x that passes throu gh the points (a,

√

a) and (x,

√

x):

√

x −

√

x − a

√

x −

√

(

√

− (

√

x −

√

(

√

x −

√

a) · (

√

x +

√

(

√

x +

√

where the last expression can be evaluated at x = a yielding



x=a

√

Our brief walk arou nd the calculus Zoo results in a discovery

of the most peculiar phenomenon: in order to be able to discuss

and compare alternative tre atments of undergraduate calculus o ne

has to be able to see it in a much wider m athematical perspective ;

in particular, some basic understanding of set-theoretic topology,

functional analysis and model theory is really useful—even if we

are talking about D onald Knuth’s method formulated in a rather

traditional and elementary language.

9.4 Some practical issues

The volume and crucial role of didactic transformation, or hidden

preparatory work of a teacher, is a spe ciﬁc feature of m athematics

teaching at the university level.

It is only natural to suggest that didactic transformation should

form a part of a professional toolbox of a mathematics lec turer.

This modest thesis, however, has ser ious implications for lecturers’

training and professional d evelopm ent.

Mathematics provides a bewildering variety of apparently in-

comparable approaches to the same topic. We also have to remem-

ber that we cannot freely bend them into the d esired shape or pick

and mix elements of different approaches: each of them has its own

internal logic which cannot be interf ered with. In that case, how do

we predict and assess the relative advantages and disadvantages

of a particular approach in teaching to a given group of students in

a given course? As a practicing teacher of mathematics, I can rely

on my co lleagues’ collective wisdom, but so far I could not ﬁnd any

usable advice in the literature on mathematics education.

Every mathematician is aware of the ex istence of so-called

mathematical folklore, the corpus of small problems, examples,

brainteasers, jokes, etc., not prop erly documented and existing

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK

104 9 Pedagogical Intermission:Di dactic Transformation

mostly in oral tradition. It is a small universe of its own, and

mathematicians’ pedagogical observations form an important part

thereof. Occasionally, these observ ations ﬁnd their way to print.

But in general the collective pedagogical experience of univ ersity

mathematicians remains uncharted territory.

One also has to take into consideration cultural differen ces be-

tween various countries and various university systems.

In Britain, where I live and work, almost every course in uni-

versity mathematics departments and most mathematics courses

in service teaching are tailor made. This is different from the usual

practice, say, in American universities where courses in so-called

“precalculus” are frequently based o n standard mass print tex t-

books and can be taught to mixed—and large—audiences of math-

ematics and engineering m ajors.

My recent experience of close reading of three dozen ﬁnal ex-

amination papers from a good Scottish university (in my ro le as an

external examiner) yet again remind ed me how much mathemati-

cal effort is invested in the developme nt of courses and the design

of examination problems—and how little of this effort is seen by

outsiders.

I argue that this hidden work of teachers is essentially a form of

mathematical research; it uses the same methods and is based on

the same value system. The d ifference is the form of ou tp ut; instead

of a peer reviewed academic p ublication (or a technical report for

the customer, as it is frequently the case in applied and industrial

mathematics) the output may take the form, say, of a detailed syl-

labus for a course which exposes classical theorems in an unusual

order, or just a page of lecture notes with a new treatment of a par-

ticular mathematical topic. The criter ion of success is the level of

students’ understanding, not ap proval by peers. The mathematical

problems solved by a lecturer in the process of course development

and conversion of mathematical mater ial into a form suitable for

teaching are far from g lamorous. They are not in the same league

as the Poincaré Conjecture or the Riemann Hypothesis; they are

more like (to give an example from my own pr actice)

“ﬁnd a way to explain to your students orthogonal diagonaliza-

tion of quadratic forms without introducing the inner product

and without ever mentioning orthogonal matrices—but make sure

that the method works”.

As mathematical r esearch stands, this kind of work is perhaps

unambitious, but it is nevertheless mathematical problem solv-

ing made very challenging by severe restrictions on the mathe-

matical tools allowed. Why are mathe matics lectur ers readily en-

gaging in this taxing and time consuming work? Their motivation

comes mostly from various external factors, starting from time con-

straints to re quests to cover particular material from colle agues

who teach subsequent courses. One may wish to add to the list

SHADOWS OF THE TRUTH VER. 0.813 23-DEC-2010/7:19

 ALEXANDRE V. BOROVIK