Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений

Подождите немного. Документ загружается.

/'•(—0.00)

=0.184.

Искомая вероятность равна 1—0,184 = 0,816.

Пример 3- Найти вероятность того, что при 100 бросаниях монеты число

выпадении герба будет находиться в пределах 45—60.

Решение. Здесь также применима функция Р (I):

51 а

"ТОО

0,50 = —1

,05;

— 0.50 = 4-0.10;

1 / 100

к==

V 0.5-0.5

=20;

= 20. (-0.05) = -1;

= 20-0,10 = 2.

Ответ

^45 =

•

(

) — •

(

) = °»

977

— 0.159

= 0,818.

Интеграл вероятностей можио получить путем иных рассуждений. При-

ведем соответствующий вывод.

Б качестве исходной возьмем формулу

Р(а<к<Ъ) = % />„(*). (1-92>

к-а

Значения Р

(к), как известно, можно получить по формуле (1.41)

Рп (к) = С*

РДО

ь п!

откуда

»Ю=кЦп-к)

93)

Подставив в формулу (1.93) факториалы п!. А!, (га—Л)-', соответствующие

формуле (1.43), получим

Рл«)-

(„"!,,

<гу=

1 ^Ц-У

После сокращений имеем _

Приняв

„П „А'О-А

— п 71

перепишем выражение (1.95)

(

тк

таЫ (-г-)* тУ'

<»•«*>

В § 8 для вероятнейшего чпслл А-.} появлений события при многократных

испытаниях была выведена формула (1.57), в соответствии с которой пр.

Вместо числа появлений события к будем рассматривать отклонение его от к

т. е.

Ак = к—пр. (1.9Г|

Учитывая (1.97), преобразуем формулу (1.96)

(*)=-4=- X

у 2 я

7/ (

АА

' \ /

ДА-

\ / ДА- \

-пр-Ьк

ДА:

(1.0?,

В предположении, что р и ? не близю! пи к нулю, ни к единице, при чвсл

иены танин достаточно большом дроби и будут малыми величинами

ир лу

а следовательно,

1. (1.99;

/(ООЧг)

Упростом в (1.98) последние два мпожителя, для чего сначала найдем вх

логарифмы

/ ДА- / да \

/ ДА- / ДА- \

(1.1(К9

Раскладывая в ряды

ДА- ДА-

по степеням и —

получаем

пр

/ ДА- АА-2

V л? / П? 2п*7« " *

Подставляя (1.101) в (1.100), имеем

. / , ДА- . / ДА- ДА*

, \

(М№

—ДА-—•

ДА"

2пр ' ' '

. (. ДАП-пд+ДЛ / ДА- Д*2 , \

ДА-2

Используя определение логарифма, можно (1.102) записать в виде

ДА- \ - -дк - +...

"Р

(1.103

('-•но

ДА- (пд-ДЛ)

Подставляя соответствующие значения последпих двух сомножителей

в (1.98) из (1.03), получаем

1 л».

АЬ

* .

П II \ ' -ЬК

. . . ДЬ

. ..

п1к)==

УШ^

е 2пр

2п

* •

{1т

Учитывая, что

ДА* Д/,-2

— «7АА-2— юАЛ-2

+ = ьГ

— = («-ад

_ —(!—;>) \к~—/,Ак* _ А к

2прд ~ %прп ' (1-Ю5)

получаем

дм

(А)— /

гпр

' • (1.106)

\ >ппрц

Подставим в (1.106) вместо ДА

ишражение (А — пр)-, тогда

(к-пру

Рп

(А)

=—===-

е ~

. (М07)

I 2 л «/*/

Формула (1.107) может служить для вычисления вероятности появлений

события А раз при п испытаппях.

В (1.107) примем

А — пр

* = ,, • (1.Ю8)

\ прц

Увеличим число появлений

на едппицу и при этом условии по формуле

(1.108) определим приращение повои перемоппои х

. А-ит>4-1

X -у Л

X —

) прц

к — п р

•

(1.109)

V а рд

Вычитая в (1.109) из верхнего выражения нижнее, получаем

Д^ =

"77===~ •

(1-1Ю)

I пря

Формула (1.107) с учетом (1.108) п (1.110) примет вид

(к)=у=-е

Д*. (1.111)

Подставим значение Р„ (А) из (1.111) в (1.02)

(1.112)

к-а

1 -

Переходя от дискретной функции е - к сглаживающей непрерывной

функции, можно в (1.112) знак суммы замепить знаком интеграла п написать

1 Р

Р(«<^<1>)"'ущ)'

<*•••. (1111)

Если пропять а

примет вид

• Л

р == -Н. то интеграл вероятностей с учетом (Мц

В формуле (1.113) пределы суммы а и Ь, относящиеся к переменной к, за-

менены пределами интегрирования, относящимися к переменной г,

а = -

а—пр

УпрЧ

Ъ-пр

\ прд

(1.115)

Нетрудно показать, что переменная х в формуле (1.113) та же, что и пере-

менная I в (1.8$).

Если числитель п знаменатель правой части формулы (Г.108) разделим ва

и. то получим

т. е., согласно (1.81), I =

Особенностью нормального закона распределения является асим-

птотичность кривой распределения относительно оси I. Вследствие

этого полная группа событий соответствует изменению I от

—

со до

+оо, в то время как заведомо известно, что значения изменяются

в копечиых пределах. Действительно, наименьшими и наибольшими

значениями ^ = р будут

71 Р

~Р

ътах = ~ — Р=1 — Р =9

(1116)

Однако практически эта особенность нормального закона при до-

статочно больших значениях п и при р, не очень сильно отлича-

ющихся от 0,5, существенного влияния на результаты не оказывает.

Чтобы убедиться в этом, вычислим интегралы

у== \ е

<Н=Р{Ь<1)-Г{-кр)

• -Лр

для некоторых примеров.

Примеры. I. Дано: я = 20; р — 0,2;

= 0,8.

Решение.

<Ш

125;

= Н.2;

-Ир=-2,24; р ф) - г (-2,24) = 1,000-0,013 = 0,987.

г,;

2- Дапо: «

—

10; />=0,4;

= 0,0.

Р е ш е и п е.

к=

1^7^24

= 6,4;

'"7

3,84;

—кр= -2,5В;

У (3,84) -

/•'

(-2,50) =0,995.

3. Дано: » = 100; р = 0,1; а = 0,9.

Решение. А = 33; Ну = 30; —Ар = 3,3 п искомая вероятность Р —

= 0.9995.

Как видим, при больших п значения р могут заметно отличаться

от 0.5, а если р близко к 0,5, то нормальпып закон дает точные ре-

зультаты даже при 10 испытаниях.

§ 11. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

• Случайной величиной называют переменную вели-

чипу. численно характеризующую случайное явление и отража-

ющую многообразие неучтенных колебаппй условий, нрн которых

производятся испытания. Таким образом, при проведении опыта при-

ходится иметь дело со случайпой величиной, конкретное значение кото-

рой неизвестно. Совокупность всех возможных значений случайной

величины составляет полную группу случайных событий (очевпдпо,

значепнн случайпой величины, получаемые при испытаниях, должны

рассматриваться как случайные события).

Примеры случайных величии:

1. Число появлеппй события или относительная частота при

многократных испытаниях.

2. Число зереп в колосьях пшеницы определенного сорта.

3. Число попаданий при стрельбе по мншеип.

4. Результаты измерений одной н той же величины в одинаковых

условиях; при этом точное значение измеряемой величины известно.

Результаты измерений будут колебаться около точного значения,

причем заранее нельзя назвать ни одного результата; можно лишь,

исходя из оныта аналогичных измерений, указать границы измене-

ния наблюдепных значений случайной величины — результатов из-

мерений или их отклонений от точного значения.

Из приведенных примеров первый занимает особое место и под-

робно рассмотрен выше. Особенность относительной частоты события

как случайной величины заключается в том, чго ее свойства вполне

определяются заданной вероятностью события и числом испытаний.

Для определения свойств любой случайпой величины требуются

более общие характеристики, о которых пойдет речь ниже. Эти

обобщенные характеристики будут пригодны п для относительном

частоты события. Таким образом, введение понятия случайпой вели-

чины целесообразно для дальнейшего обобщепия понятий теории

вероятностей.

Среди различных типов случайных величин наибольший интерес

представляют прерывные (дискретные) и непрерывные случайпые

величины.

11 р е р и в и о и называют случайную величину, которая мо;щ.

принимать отдельные, изолированные значения с определенными

вероятностями. Число возможных значении прерывной случайной

величины можег быть конечным н бесконечным. Рассмотрим лишь

прерывные случайные величины с конечным числом возможных зна-

чений. которые можно заранее указать (например, число попаданий

при трех выстрелах: 0. 1. 2, 3; относительная частота попаданий

при трех выстрелах: 0. 1.3. 2/3. 1: число появлений отрицательной

ошибки при пяти измерениях: 0. 1.2. 3, 4, 5: число появлений собы-

тия при многократных испытаниях).

Непрерывно й называют случайную величину, возможные

значения которой непрерывно заполняют некоторые конечные или

бесконечиые

ромежутки.

Правор. Производится стрельба по цели, представляющей квадрат со сто-

роной о. Начало координат совпадает с центром квадрата. Событию «попадание

в цель» соответствует условие

15/1=^4

Таким образом, если случайное событие «попадайте в цель» произойдет,

можно утверждать, что координаты точкп попадания х и у заключены в преде-

ч , а

лах от —до + но нельзя перечислить возможные зпачепия координат точек

попадания.

Разумеется, конкретные значения случайной величины при огра-

ниченном числе испытаний могут заметно отличаться одно от дру-

гого. и в этом смысле она не кажется непрерывной, хотя эти значе-

ния и нельзя перечислить заранее. Однако речь идет о возможных

значениях случайной величины, т. е. о таких, которые она может

принимать в процессе опыта. Число иаблюдеипых значений случай-

ной величины всегда конечное.

§ 12. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

СЛУЧАЙНЫХ ВЕЛИЧИН

Для полной характеристики прерывной случайной велнчпиы не-

достаточно знать возможные ее значении: необходимо также знать

вероятности, соответствующие этим значениям.

Соотношение, прн помощи которого устанавливается связь между

возможными значениями случайной величины и соответствующими

им вероятностями, называют з а к о и о м раслреде л е и и я

с л уча иной в е л ич ин ы.

Закон распределения прерывной случайной величины может

быть задан: 1) аналитически. 2) чнеленио и 3) графически.

1. Примером а н а л и т и ч е с к о г о выражения закона рас-

пределения для прерывных случайных величин может служить

вероятность появлений событии к раз при п испытаниях, вычисляе-

мая но формуле (1.41).

4Я

В этой формуле каждому возможиому значению числа появлений

события к

{

(г = 0, 1, 2, 3, . . п) ставится в соответствие вероят-

ность Р

(к).

2. Закон распределения прерывной случайной ьеличяны можно

задать численно в зпде таблицы распределения, в которой

перечислены возможпые зпачепия случайпой величины и соответству-

ющие им вероятности,

X»

рГ>

*п

Рп

Таблицу распределения часто называют также рядом распределе-

ния случайной величины X.

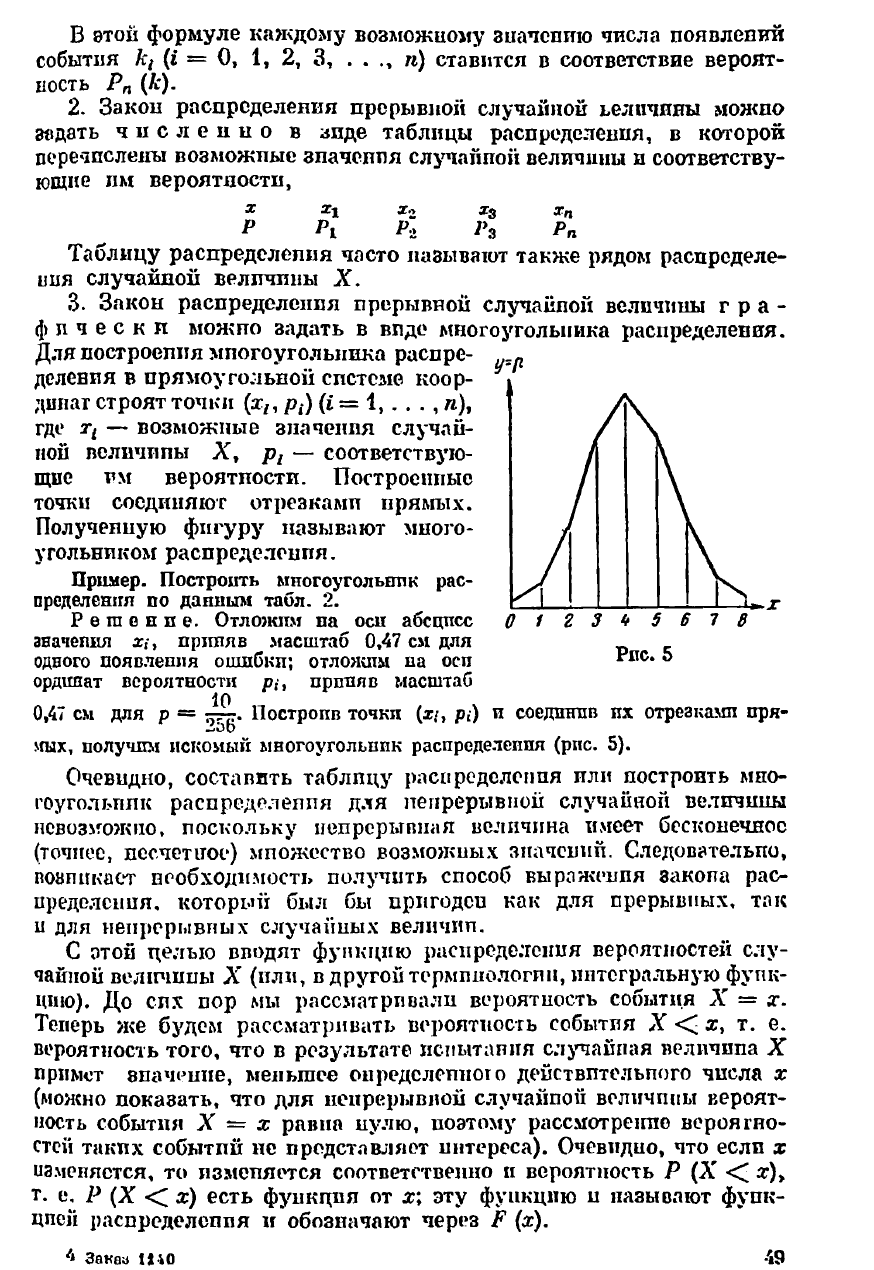
3. Закон распределения прерывной случайпой величины гра-

фически можпо задать в виде многоугольника распределения.

Для построепия мпогоугольника распре-

деления в прямоугольной системе коор-

динат СТрОЯТ ТОЧКИ (Х[, р

) (1=1,..., л),

где т

{

— возможные значения случай-

ной величипы X, р

— соответствую-

щие им вероятности. Построенные

точки соединяют отрезками прямых.

Полученную фигуру называют много-

угольником распределения.

Пример. Построить многоугольник рас-

пределения по данным табл. 2.

Р е га е п п е. Отложим па оси абсцисс

значепия я,-, приняв масштаб 0,47 см для

одного появления ошибки; отлояшм на осп

ординат вероятности рприняв масштаб

0,47 см для р = ^гт:. Построив точки (г», р,) и соединив их отрезками пря-

них, получим искомый многоугольник распределения (рис. 5).

Очевидно, составить таблицу распределения или построить мно-

гоугольник распределенпя для непрерывной случайной величины

невозможно, поскольку непрерывная величина имеет бесконечное

(точнее, несчетное) мпожество возможных значений. Следовательно,

позпикает необходимость получить способ выражения закопа рас-

пределения, который был бы пригоден как для прерывных, так

и для непрерывных случайных величии.

С этой целью вводят функцию распределения вероятностей слу-

чайной величины А" (или, в другой терминологии, интегральную фупк-

цшо). До сих пор мы рассматривали вероятность события А' = х.

Теперь же будем рассматривать вероятность события X ж, т. е.

вероятность того, что в результате испытания случайная величина X

примет вначепие, меньшее оиредслепното действительного числа х

(можно показать, что для непрерывной случайпой величины вероят-

ность события X — х равна нулю, поэтому рассмотрение вероятно-

стей таких событий не представляет интереса). Очевидио, что если х

изменяется, то изменяется соответственно и вероятность Р (А' < дг)>

т. е, Р (X < х) есть функция от х; эту фуикцию и называют функ-

цией распределения и обозначают через Р (х).

4 Заказ 1140

IIгак, фуикцпя распределения определяется равенством

Г(х)=Р(Х<х). (1.117)

Исходя пз определения функции распределения, легко доказать,

что она обладает следующими СВОЙСТВАМИ:

1) значения функции распределения принадлежат отрезку [0; 1];

2) функция распределения неубывающая;

3) если возможные значения случайной величины принадлежат

интервалу (я, Ь), то

/*(х)=0 при ггСя;

Г (т)

при .с^Ь.

Функция распределения непрерывной случайпой величины не-

прерывна (и непрерывно дпффереицнруема). поэтому такую функ-

цию распределения можно дифференцировать.

Плотностью распределения вероятностей непрерывной случайной

величины * называют производную от ее функции распределения.

т. е. плотность вероятности определяется равенством

/<*)«/'(*).

Можно доказать, что плотность вероятности / (я) обладает следу-

ющими свойствами:

Плотность вероятности еегь не отрицательная фуикцпя, т. е.

/(*)> 0.

2. Несобственный интеграл от плотности вероятности в пределах

от —оо до +оо равен единице, т. е.

со

• со

В частности, если возможные значения случайной величины при-

надлежат интервалу (я, Ь), то

)'/(*) <** = !-

3. Вероятность того, что непрерывная случайная величина в ре-

зультате испытания примет значение, принадлежащее интервалу (я.

/>). определяется равенством

= \П*)

<**•

В данной работе будем рассматривать главным образом случай-

ные величины, подчиняющиеся нормальному закопу распределения.

Почти все случайные величины, с которыми приходится иметь дело

геодезисту, распределены нормально.

* Иногда ее называют «дифференциальная функция распределения», «дпф

ферешшалъный закон распределения*.

§ 13. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ

(ПАРАМЕТРЫ РАСПРЕДЕЛЕНИЯ) СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Свойства случайной величины могут характеризоваться несколь-

кими параметрами. Важпейшио пз пих — математическое ожидание

случайной величины, которое обозпачнм через М (X), и дисперсия

В (X) = сг

(X), корень квадратный из которой о (X) называют

стандартом, пли средним к в а д рати чески м от-

клонением. Остальпые параметры случайных величип рассмат-

риваются в главе II.

1. Математическое ожидание

Математическим ожиданием М (X) прерывной

случайпой величины X называют сумму произведений всех возмож-

ных значений случайной величины на соответствующие им вероят-

ности.

Таким образом, при наличии таблицы распределения но опрсделе-

ппю математического ожидания и при условии, что число возможных

зпачешш случайной величины X конечное, можпо записать

М (X) = адо-Ьх

+...+х

= 2

1Р1. (1.118)

где = 1. поскольку появление одного из возможных значе-

(-1

ний х

есть достоверное событие.

Если выражение математического ожидаиия (1.118) распростра-

нить на дискретные величины, имеющие бесконечное число возмож-

ных значений х

, то^

Л/(Х)=]щУед, (1.119)

«-00

причем предполагается, что ряд (1.119) сходится абсолютно.

Учитывая, что в (Т.118) и (1.119) 2 р

{

= 1, иногда пишут

«-1

<р<

ЛЦХ^-Ц (1.120)

2 Я

«-1

Формула (1.120) позволяет дать механическую пптерпретацпю'ма-

тематического ожидаппя: М (X) — абсцисса центра тяжести системы

точек, абсциссы которых равпы возможным значениям случайпой

величины, а массы, помещенные в эти точки, равпы соответствующим

вероятностям.

А*

Математическим ожиданием непрерывной случайной величины

называется интеграл

Л/(А') = | х/(*)<!*. (1.121)

-со

причем предполагается, что интеграл сходится абсолютно; здесь

/ (г) — плотность вероятности распределения случайпой величины X.

Пример. Вероятность попадания в цель при выстреле р — 0,5. Определяя,

математическое ожидание числа попаданий при четырех выстрелах.

Решение. Вероятности возможною числа попаданий О, 1, 2, 3, 4 со-

ответственно равны ^

Р,(0) =

С°у•/><»=

1.(4-) ; р

(0)

= 0,0625.

Р* =4 • (т)

Рл

(1) = 0,2500.

Ра{= Р

(2)

= 0,3750.

Ра (3)

= =4

•

(у)'; Р

{3) = О,2500.

Рл (4)

= С^°/<« =

1 •

(у)':

Р*

(4) =0,0625.

Контроль: V Р

(/,•)

= 1.00И0.

А» О

Математическое ожидание числа попаданий прп четырех выстрелах

М (А')=0

- 0,0625

I -

0,2504 2

0.375-}-3

•

0,250 + 4.0,0625 = 2.

Реальный смысл математического ожидания станет яснее, если

установить его связь со средним арифметическим. Заметим, что сред-

ним арифметическим называют величину, вычисляемую по формуле

Покажем, что при неограниченно большом числе испытаний пре-

делом среднего арифметического является математическое ожидание

случайной величины. Рассуждения будем вести применительно к фор-

муле (1.118), т. е. для прерывных случайных величин, отметив прп

этом, что все полученные выводы можно распространить и иа ысире-

рывиые случайные величины, пользуясь формулой (1.121).

Пусть в результате N иснытаний случайная величина х приняла

следующие зиачения:

появилось т

раз

х., ь т, »

Х3 » Шд 9

ь т

» ,

г,;