Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений

Подождите немного. Документ загружается.

§ 9. ПРЕДЕЛЬНЫЙ ЗАКОН МУАВРА - ЛАПЛАСА

(НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

ПРИ МНОГОКРАТНЫХ ИСПЫТАНИЯХ)

Биномиальное распределение вероятностен более или менее при-

годно дли решения практических задач лишь при ср^вннтелыю

небольшом числе испытании (не более 10—20). С увеличепием числа

испытании и вероятности отдельных значении числа появлении со-

бытия уменьшаются и при большом п становятся ничтожно малыми.

У то почти очевидно, если учесть, что число членов биномиального

распределения равно п 1, а сумма его членов всегда равна еди-

нице.

При большом числе испытаний практический интерес может пред-

ставить лишь решение следующей задачи: какова вероятность того,

что событие совершится в пределах от а до Ь раз. т. е. совершится

или а раз. или а + 1 Р

аз

Н1П а

- раза, или а + 3 раза, и т. д.,

или Ь раз. Согласно теореме сложения, вероятность такого слож-

ной» события (суммы событий) равна сумме вероятностей составля-

ющих событий, т. е. Р

(а) + Р

{а + 1) + Р

(а + 2) + ... +

-!- Р

(Ь).

По подсчет такой суммы вероятностей с использованием формулы

(1.40) црн большом п чрезвычайно сложен.

Значительно проще указанная задача решается на основе так

называемого нормального закона распределения вероятностей, пол-

ный вывод которого впервые дан Лапласом, использовавшим для

этого результаты, полученные ранее Муавром. Поэтому нормальный

закон называют еще законом Муавра — Лапласа.

Нормальный закон распределения дает достаточно точные резуль-

таты лишь при большом числе испытаний. Но этой причине его отно-

сят к предельным законам. При п ^ 20 и значениях />. достаточно за-

метно отличающихся от 0 и от 1 (иными словами, не очень сильно

отличающихся от 0,5). нормальный законо беснечивает результаты,

практически не отличающиеся от тех, которые дает биномиальный

закон *. Получим нормальный закон на основе биномиального. При

этом примем во внимание, что биномиальный закон распределения

имеет два существенных недостатка.

Р>о-первых. это закон дискретный, т. е. функции Р

(к) по непре-

рывная. а изменяется дискретно (прерывно). Поэтому сумм}' верояг

постой Я,

(«)

/»«

(в-г»)+/»«(«+ 2)+. -

1'п {к)

нельзя заме-

к—о

нить интегралом даже при большом числе испытании. Указанную

сумму можно получить лишь непосредственным вычислением всех

слагаемых.

Второй недостаток биномиального распределения заключается

в том, что ряд распределения (<7 + р)

зависит от двух параметров —

п и р, что практически лишает возможности табулировать значения

* При значениях р, сильно отличающихся от Циются другие

.иконы.

Л Ллказ 1140

вероятностей Р„ (к); для разных значении вероятности испытуемого

события р и для разных значений числа испытаний п пришлось бы

составлять множество таблиц.

Нормальный закон распределения не имеет указаппых недостат-

ков биномиальпого распределения. Кроме того, п это не менее важно,

нормальный закон,.как увпднм ниже, распространяется на очень

широкий класс случайных явлений и попользуется пе только для

подсчета вероятностей попадания в определенные пределы числа со-

вершении события, но и в очень многих других практически важных

случаях.

Перейдем к выводу нормального закона. Стремясь как можно

лучше сохранить положительные свойства биномиального закона,

учтем следующие его собенностп:

1) аргумент к биномиального

распределения изменяется дис-

кретно и равнопромежуточно, че-

рез единицу;

2) наибольшая вероятность со-

ответствует значению к

я&пр.

Изобразим графически некоторое

биномиальное распределение

(д + р)«.

Для этого по оси X последо-

вательно отложим отрезки, равные

единице. На первом отрезке по-

строим прямоугольник с высотой

/г

= Р„ (0). на втором отрезке —

прямоугольник с высотой А, =

— Р

(1), на третьем — с 1и =

= Р

(2) и т. д. до К = Р„(п).

Площадь, ограниченная снизу осыо X, а сверху—ступенчатой ло-

маной, равна единице (сумма вероятностей полной группы). Харак-

тер распределения иллюстрируется верхней стуленчгтгой ломаной.

С увеличением п высоты ступенек этой ломаной (т. е. разности ве-

роятностей соседних значений) уменьшаются, а сама ломаная линия

все более приближается к оси А\ расширяясь вправо. Сказанное

иллюстрировано па рис. 2 для функции Р

{к) и Р

(к) при р -- 0,4.

В нормальном законе ступенчатая ломаная линия заменяется не-

прерывной плавпой кривой, а выбором аргументов, соответству-

ющих комплексу условий, этой кривой придается стандартный впд.

Конечная цель первого этана вывода — получение такой функ-

ции / (Н), которая позволила бы вычислять искомую сумму вероят-

ностей как интеграл

|/(|)<К, где

= |

= ф(а), |

=Ф(Ь),

р^Ър-е*

о 1 г з *

РМГ-М

^н

0 1 г 3 •< 5 6

Рис. 2

а соответствует изменепию к па единицу. В качестве аргумента

функции /(&) возьмем отклонение относительной частоты испытуе-

мого события от его вероятности. Такой выбор аргумента придает

уже большую общность различным частным случаям.

В качестве аргумента искомой функции принят

г-т-р. <

158

Тогда (Iс. соответствующее изменеишо /с на единицу, будет равпо

ИЛИ

Учитывая значение Ле, напишем для искомой функции у = / (5)

У=-пР„(к), (1.60)

откуда

(А-)-»-^'

пли. согласно (1.59),

(к) = у<1Ъ = ЦЪ)<1Ъ. (1.01)

Н&пдем вид функции у = / (|). Для этого напишем два равенства

Ук-пР

(к) Г

Разделив у

к+1

на у

, получим

УЫ __

/>п(*

V* Рп (к) '

или, учитывая (1.41),

гк+1 „я-А-1

„к-т-1

к+1

Ук+1

п Я Р

—

Ук с

с* ' я '

Так как

(1.63)

п\ п\ к\Цп-к)\ ^ п-к

к (А+ 1)1 (л—к—1) ! " А*! («—А-) I

(А

+ 1) I (п-к — 1)

1 А

+ 1 *

ТО

Ук* 1 _ . Р

1Тк

+ 1 ? *

64)

Обозначая — ук ~г А^/л» можем паппсать

Ук + ЬУк

А."* _ (д—к) р ^

Ук ~ У к (А-г1 )д '

или

_ (

—к) р

— (А--.- 1)

д __ пр—кр — кд—д _ пр — д—к{д + р)

Ук (* +1) д кд+д кд

Но

+ Р = 1. поэтому

Ат/Д, пр—к-

У к

функ

вскство (1.65) в впде

(Г.С5)

Желая получить функцию аргумента | р. напишем ра-

—- —

Ду* »

"*~ "

йг

1Г4-Т

Так как предполагается, что п достаточно велико, то в числителе

и знаменателе дроби (1.(56) отбросим величину Тогда можно на-

писать

Ук Ч(Р + 1)

(1.67)

Теперь перейдем от дискретного биномиального закона распре-

деления к непрерывной функции у = ] Для этого, учтя, что

= [см. (1.59)1. напишем дифференциальное уравнение

= —^Ц-Л. (1.08)

У Ч(Р-п) *

Из решения уравнения (1.6В) получим непрерывную функцию

= / (Ё), сглаживающую биномиальное распределение. По предва-

рительно выполним некоторые упрощения, используя разложение

в ряд Тэнлора *:

,«*? "1

" ^

Л .

л-

п п п

- « + -I

•

или

дц п п п

"Г —. . (1.69)

Проинтегрировав уравнение (1.69), получим

(постоянную интегрирования можно нредстивлять в любом ниде).

• Уравнение (1.68) можно было бы проинтегрировать и непосредственно,

не прибегая к разложению в ряд, но тогда мы получили бы функцию, не удоб-

ную для практического применения.

Если иметь в виду, что значении р не очень сильно отличаются от

0,5. то в правой части равенства всеми члепами разложения, кроме

первого, можно пренебречь. Это следует из того, что абсолютные

значения ^

больших п зпачпгельпо меньше единицы, поэтому

ряд быстро сходится.

Теперь имеем

откуда

Так как величина ^ всегда положительна, то введем обозначения

^ У р<7

Итак,

(1-72)

- —

у^С-е

(1.73)

(коэффициент

/« в показателе степени оставлен с учетом использо-

вания в дальнейшем существующих таблиц).

Кривая, выражаемая формулой (1.73). расположена выше оси абс-

цисс (показательная функция отрицательных значений не принимает)

и симметрична относительно оси У (функция четная). Ветви этой

кривой асимптотически приближаются к оси Л*.

Определим значепие постоянной С. Для этого вспомним, что

площадь под ступенчатой ломаной линией биномиального распределе-

ния равна единице. Ввиду этого поставим условие, чтобы площадь

под кривой нормального распределения также была равна единице

+ СО 1С1

С С с

* 1/6 =

(174)

—со

(пределы —сю и -г<х> поставлены с учетом асимптотичности кривой).

Для определения значения интеграла в левой части равенства

(1.74) введем обозначение

0.75,

откуда

— (1-76)

Теперь можно написать

_ +СО

12 Р

С-^- ] =

(1.77)

-со

(пределы интегрирования, очевидно, не изменятся).

г,;

Учитывая, что интеграл в левой части этого равенства равеи

Vл (интеграл Пуассопа), получаем

Отсюда

-71Г' "'

78)

Принимая во внимание (1.71), (1.72), (1.78), окончательно полу-

чаем искомую функцию у — / (Е) в виде

и -

—

лч

'"ТЁГ'

•

Для вероятности числа появлении события к и соответствующего

€му значения § — р пмеем, учитывая (1.61),

(к) = = Г

* «*!. (1.80)

Выражение (1.80) показывает, что вероятности отдельных значе-

ний

будут ничтожно малы при п большом [см. (1.59)].

Заметим, что ординаты кривой (1.79) называют «плотностью ве-

роятности» нормального распределения.

Функция (1.79) пеудобна тем, что имеет переменный параметр

-У-к-

вследствие чего се нельзя изобразить одним графиком или табули-

ровать таблицами с одним входом: фактически это функция двух

переменных — с, и к, а вид кривой у = / ($•) зависит от параметра Л.

Поэтому целесообразно ввести новую переменную

(1.81)

откуда

(1.82)

Теперь выражение (1.80) примет вид

* А

1Л)-РК) = Р(«)«-р==-е

Л1 . (1.83)

Кривая распределения становится стандартной, а соответству-

ющая ей функция $ (I) принимает вид

1 -4

Кривая (1-84) показана на рис. 3. Таблица значений функции

(1.84) приведена в прпл. 1. При помощи указанпой таблицы значе-

ние Р

(к) получают следующим образом.

1. Находят вначеппе I по формулам

I—-р

рч

(1.85;

1=к%

2. По таблице прпл. 1 находят величину

•М-75Г*"*"-

3. В соответствии с формулами (1.59) и (1.82) вычисляют

61 —

—•

4. Получают искомое значение

Рп

(Л)

=4» (О Л.

(1.86)

(1-87)

Пример 1. Найтп вероятность появления белого шара С раз при 10 испыта-

ниях, еслп в урне имеется 4 белых гаара п 6 черных (шары в урну возвращаются).

•Л***'

/ -

«А

0.2 \

1 » \ 1

0.1 N.

1 1-

•з -г -1 о *г *2 *з

Рпс. з

Решеппе. Дано: п = 10; к = 6; р — 0,4; д = 0,6. Применяем формулы

(1.85), (1.86), (1.87) и таблицу прпл. 1.

С т/ 10

1. -0.4-0.20;

= у

/ =

6.4'.

-0.20 = 1.283.

2. Из таблиц прпл. 1 получаем

г|>

(1,288) =0.1740.

6.44

3. ^ = -^- = 0,64'..

4. Ответ:

(А-)

= 0,174 •0.С

14 = 0,112.

Биномиальное распределение дает

Рп (к) = С«

(0,4)° • (0.0)

=0.112.

Пример 2. Найти вероятность выиадспии герба 4 раза при 10 бросащ,

Нх

поветы.

Решение. Дано:

и =

10; •

А*=»4;

р — 0.5:

<7-^0.5.

I. — 0.5

—

—0.10;

"|/ 10

/ = /,^=0.632.

2. ф (0,632) = 0,327 [знак минус прп аргументе / опущен, так как фупк1

Шя

•ф

(0 четная, т. е. ф (—4) = ф (01-*

6 32

3. л =—-=0,632.

4. Ответ:

Рп (к) =

</)

•

<П=0,327

•

0.632 = 0,207.

Биномиальное распределение дает Р

(Щ

— 0,205.

Пример 3. Найти вероятность выпадения четырех очков 2 раза при 10 бро-

сав иях игральной кости.

Решение. Дано:

пг= 10; к =

р=~-=0,1667; <у=0.8333.

1. 5=0,20 — 0.1667 = 0.0333;

Г Ю

]г

~~ V 0,1667

•

0,8333 '»

/ —8.47

•

0,0333=0.282.

2. ф (0.282)=0.383.

8.47

3. И —0,847.

4. Рп

(А

)

=0,383

•

0,847 0,32.

Биномиальный

закон дает Рц 0,29. Здесь расхождение оольше, таи как

вероятность р сильно отличается от 0,5 и п мало.

Как видим, даже при 10 испытаниях нормальный закон уже

дает ответы, мало отличающиеся от биномиального распределения.

При п > 20 и значениях р, пе очень сильно отличающихся от 0,5,

а также при ^ не очень больших результаты достаточно хорошие.

Однако, как уже указано, при большом числе испытаний вероят-

ности Р

(к) становятся настолько малыми, что их вычисление те-

ряет практический смысл.

§ 10. ИНТЕГРАЛ ВЕРОЯТНОСТЕЙ

Как указывалось, при большом числе испытаний практический

интерес может представить лишь подсчет значения — вероятности

того, что число совершений события попадет в пределы от а до Ь.

Преимущество нормального закона перед биномиальным и заклю-

чается в том, что значение Р

можио получить как определенный и»-

4о

теграл,, нс вычисляя значений всех Р

(к) каждое отдельно. Иными

словами, сумма вероятностей ^ Р

(к) заменяется иитегралом

к -и

Ь 1

(II. (1.88)

где пределы (

п 1

можно получить как функцию а и Ь по формулам

(1.85).

Определенный интеграл, как известно, есть функция пределов

интегрирования. Чтобы уменьшить число аргументов этой функции

до одного, один из пределов обычно делают стандартным, что позво-

ляет табулировать зпачеппя интеграла вероятностей как функцию

одного переменного.

Наиболее удобен интеграл вероятностен, симметричный относи-

тельно оси У,

где ± §

— заданные пределы отклонения относительной частоты

от вероятности.

Выражение (1.89) показывает, что значение увеличивается

при увеличении абсолютной величины /. По I = Уоткуда

видно, что при заданном значении | = р, как бы оно мало

не было, с увеличением п вероятность может стать как

угодно близкой к единице. Тем самым доказана приведенная в § 3

теорема Я. Бернуллн. Ввиду четности подынтегральной функции

(1.89) .можно написать

' Л.

\ <• <// =

<!>(*).

(1-90)

л *

Функцию (1.90) называют интегралом вероятностей. Нетрудно

видеть, что этот интеграл есть функции одного переменного I, т. е.

Р-Ц = Ф (/), где I = к |6

|, - ъ

-р; - р; ± а -

заданные пределы отклонений к от к

= пр.

о ' ~

Таблпца значений Ф (() = -4=- \ е

приведена в и рил. 2.

1 2л. ^

Иногда удобнее применять таблицы интегралов

' <<

^ г~ 41 А'('). (1.91)

2л

-со

где { может принимать как положительные, так п отрицательно

значения.

Функцию*/

(0 называют иногда функцией нормального распреде.

ленпя. В прил. 3 дается таблица значеппй функции Р (I).

-И

Так как функция е

в элементарных фуикцпях не пнтегрв.

рустся, то значения Ф (/) и Р (/) при составлении та^ппц вычисляю;

путем разложения в ряд функции е

Таким образом, все практические задачи можно решать при по.

мощи таблиц значепий Ф (/) и Р (/) (прил. 2 п 3). Покажем это

примерах *.

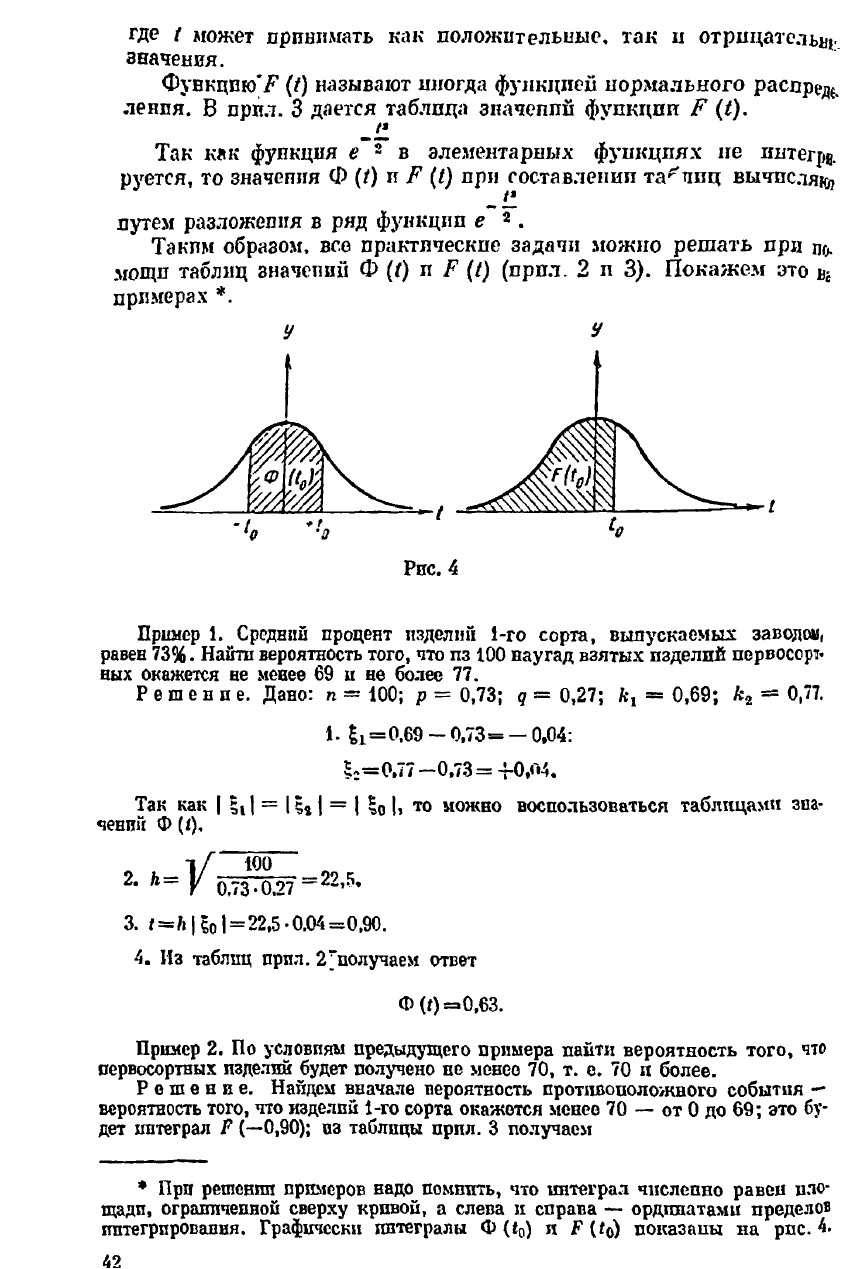
У У

Рис. 4

Пример 1. Средний процент изделий 1-го сорта, выпускаемых заводом,

равен 73%. Найти вероятность того, что пз 100 наугад взятых изделий первосорт-

ных окажется не менее 69 и не более 77.

Решение. Дано: п = 100; р = 0,73; ц = 0,27; А, = 0,69; к

— 0,77.

1. ^=0.69 - 0,73= -0,04:

;

=0,77

—0,73

= -г0,О4.

Так как | 511 = 1| = I !о

т0

можно воспользоваться таблицами зна-

чений Ф (/),

-\[ 100

А=

У 0.73-0.27 =

з. 1=22,5.0.04=0,90.

4. Из таблиц прил. 2^получаем ответ

Ф (0=0,63.

Пример 2. По условиям предыдущего примера пайти вероятность того, что

первосортных изделий будет получено не менео 70, т. е. 70 и более.

Решение. Найдем вначале вероятность противоположного события

—

вероятность того, что изделпй 1-го сорта окажется менее 70 — от 0 до 69; это бу-

дет интеграл Р (—0,90); аз таблицы прил. 3 получаем

* При решении примеров надо помнить, что интеграл чпелепно равен пло-

щади, ограниченной сверху кривой, а слева и справа — ординатами пределов

интегрирования. Графически интегралы Ф (е