Большаков В.Д., Гайдаев П.А. Теория математической обработки геодезических измерений

Подождите немного. Документ загружается.

Отметим одио свойство случайных величин, подчиняющихся любому сим-

метричному закону распределения, а следовательно, и нормальному закону:

математическое ожидайне л 106011 нечетной степей» отклопеипя |

—

X — М (X)

цаино нулю. Это свойство следует из симметричности кривой распределения

относительно осп К. Если рассматривать'математпческое^ожлдаипе случайной

велпчппы как предельное среднее зпачеппе, то каждому положительному зиачо-

ппю

-Ь

Б/

4+1

должно соответствовать такое же отрицательное зпачеппе —

тан как число их появлений в нределе должно Сыть одинаковым, из-за чего прои-

зойдет полная компенсация. В частности,

<1.175)

Несоблюдение отмеченного свойства нечетных степеней ^ служит одним из

основных признаков отклонения рассматриваемого распределения от нормаль-

ного закона.

Приведем несколько примеров применения полученных формул

(1.173) и таблиц значений Р {I) п Ф (/) (см. прпл 2 и 3).

Пример I. Л/ (X) = 145,3; о (X) = 2,1; найти вероятность попадания зна-

чения случайной величины прп одном испытании в^пределях от 143,2 до 147,4.

Решение. Вычислим 631

*а

= 143,2-145,3=-2,1;

147,4—145,3= +2,1; ^ = = ~ 1; '^"ХТ

= 1

Так как =» = 1, то по таблице зоаченпй фупкцпи Ф(0 (прпл. 2)

на идем

Ф (1) = 0,083.

Пример 2, Средний процент выпуска брака продукции не заводе, получен-

вый за много дней, равен 1,80%. Стандарт этой величины а == 0,20%.

Найти вероятность того, что в отдельные дни процент брака будет нахо-

диться в пределах от 1,5 до 2%.

Р е ш е н_и е. По условию з

р — 1,80; о = 0,20, откуда

1. €1=1.50—1,80= -0,30; 2,00-1,80- +0,20;

0,30 0 Л) ,

оЖ

и50;

'*= + оЖ

= + ьо

°-

' I*

Здесь применим таблицу Для Р {I) = -ут==- ^ «

(прпл. 3).

*"" -со

2. Р (+1) =0,841; Р{—1,50) =

0,067.

Ответ: 0,841-0,067 = 0,774.

Получеппый ответ означает, что пз каждых 100 дней работы приоллзптелыю

77 дней процент брака продукции на заводе находится в пределах 1,5—296-

Прнмер 3. Используя исходпые данные предыдущей задачи, найтп тот

предел, которого пе превысит выпуск брака продукции завода с.вероятностью

Р * 0,4.

Дано:

ср

^1,80; а =

0,20;

/>=0,40; г

=0; ^=-1,80.

Найти:

.г

— ?

1 ЯО

Рошевпс. = — = —9. Практически моишо считать, что /а,

—оо. Поэтому воспользуемся таблицами интегралов Р (/). Потенцируя, нахо.

дпм /„ соответствующее Р(1

) — 0,40.

и = - 0,254; = а . ь = - 0,20

•

0,254 = —О,05.

Ответ:

= т. е. (1,80—0,05).

Ответ означает, что приблизительно 4 дня из 10 выпуск брака на завом

ве превысит 1,75%.

Пример 4. Для установления процентного соотношения размеров выпу-

скаемых обувной промышленностью солдатских ботшгок был произведен обмер

ступней солдат в одной из частей и подучепы следующие результаты: средняя

длппа ступня х

ср

= 25,5 см, стандарт а = 2 см. Значению лг

ср

= 25,5 см соот-

ветствует размер ботггаок Лг 41. Изменению размера па один номер соответствует

лзмеирвпе длины стушги па 1 см.

Найтп наиболее правильное процентное распределение по померам выпуска-

емых ботинок. Здесь удобно воспользоваться таблицами Ф (/)•

Решение. Ступени изменения х следующие:

от 20 см до 21 см — ботинки Лг 36

» 21 » » 22 » —

К: 37

» 22 > > 23 » —

0 Л« 38

» 23 » » 24 » —

Л*

» 24 » » 25 » —

№ 40

» 25 » » 26 » — »

№ 41

» 26 » » 27 » —

№ 42

» 27 » » 28 » —

Ле 43

» 28 » » 29

к>

— » -\г 44

» 29 » » 30 » — »

* 30 » » 31 » —

№46

Найдем теперь ступени изменения ±

НК

_50

Л?

36 я

Л?

46 — от ±2,25 до ±2,75

Л*

37»

Л»

45 — » ±1,75» ±2,25

Ле

№ 44 — » ± 1,25 » ±1,75

Л5

39 * Л: 43 - » ±0,75 » ±1,25

Лг

40 » 42 — » ±0,25 » ± 0,75

*&41» ±0 ±0,25

Далее при помощи таблицы Ф(г) (прпл. 2) получим, что необходимо вы-

пускать

Л«

36 и

Л*

46 по 0,9%

Л<г

37 » № 45 » 2,8%

X»

» Л

44 » 7,1%

№39»

43 » 11,6%

№ 40

» Л:

42 » 17,4%

№ 41

19,8%

Кроме того, 0,6% необходимо выпускать по специальным заказам, поступа-

ющим ЕЗ частей.

§ 16. О НЕКОТОРЫХ РАСПРЕДЕЛЕНИЯХ,

ОТЛИЧАЮЩИХСЯ ОТ НОРМАЛЬНОГО

1. Равномерное распределение

Прп обработке результатов паблюдешш часто нриходится^иметь

дело со случайными величинами, плотность всроятпостп которых

имеет иостояппое значение в некотором конечном интервале.

С4

Указанное распределение носит название равномерного Плот-

ность равномерного распределения случайной величины X выра-

жается функцией (рис. 6)

Ы*)

\ 2а

при а — а ^ зе^а -}

•а},

(1.176)

где а ± а — пределы изменения х, а — абсцисса центра интервала.

Таким распределением обладают, папример, ошибки округлений.

График функции /, (х) показан на рпс. 6. Так как график функ-

ции /, (я) изображается прямоугольником, распределение часто на-

зывают прямоугольным.

Фуикцпя распределения Р, (#)

имеет вид

(*)

0 при

эг

а —

х+а—а

^— при а

—

1 нрц

аО>в

+ а

У 1

-»» I

(1.177) а-а -0,2 а *0,2

Убедимся в том, что. если воз- Рпс. 6

можные значения равномерно рас-

пределенной случайной величины X принадлежат интервалу (а — а,

а + а), то вероятность попадания X в этог интервал равна единице:

о+а

Г (а + а) —(а—а) 2а

+ = ^ ^ = ~ =

а-а.

Найдем числовые характеристики равномерного распределения!

математическое ожидание и стапдарт. По определению математиче-

ского ожидания

с+сс о+а а+а

С 8х 1 Г* ж- I 1

а-а. а-а а-а

ПЛЫ

Л/(А•)=«. (1.178)

Вычислим дисперсию, а затем стандарт равномерного распределе-

П (Х)=М (X

) - [М (.V)]*. (1-179)

а+а о+а

ния

Найдем

. а-а а-а

Сделав элементарные выкладки, иолучим

ОС-

л/(А'

)=— +

5 Закоа н ю

(1.180)

Принимая во внимание (1.178), (1.179) и (1.180), окончательно

получаем

а ' "81)

<-«>=тг)

Напомним. что а — наибольшая величина, на которую может

отклониться зпаченпе случайпой величины от ее математического

ожидания, т. е. а — абсолютное знячепне предельного отклонения.

2. Закон распределения Пуассона

При выводе нормального закона распределения для отклонении частоты

от вероятности предполагалось, что р — вероятность испытуемого события

—

не очень сильно отличается от 0,5. Для р, близких к нулю или к единице, вор»

мальвып закон плохо обосновав. В этих случаях лучпю применять закон рас-

пределения Пуассона для событий с малой вероятностью р. Если событие имеет

вероятность, близкую к единице, то закон Пуассона применяют для противопо-

ложного события с вероятностью д

—

1 — р. Очевидно, вероятность числа к

появлений события равна вероятности числа (п — к) появления противополож-

ного события при числе испытаний л.

Закон распределения Пуассона выражается формулой

Р(к)=].Т«~'

» (1-182)

где ко = пр, т. е. величина, постоянная при заданном л.

Величина к может принимать только целочисленные значения, теоретиче-

ски ничем не ограниченные, по, конечно, А-^п. Очевидно, что^вороятность по-

падания числа к в пределы от 0 до а равпа

№•0

а 01 Й! до а,

Ь-С,

к-Ог

Если потребуется получить вероятность

V *о

л»

С+1

то, разумеется, выгоднее получить вначале

а затем

Р(/с>в) =

1 —

Р(А^а).

г,;

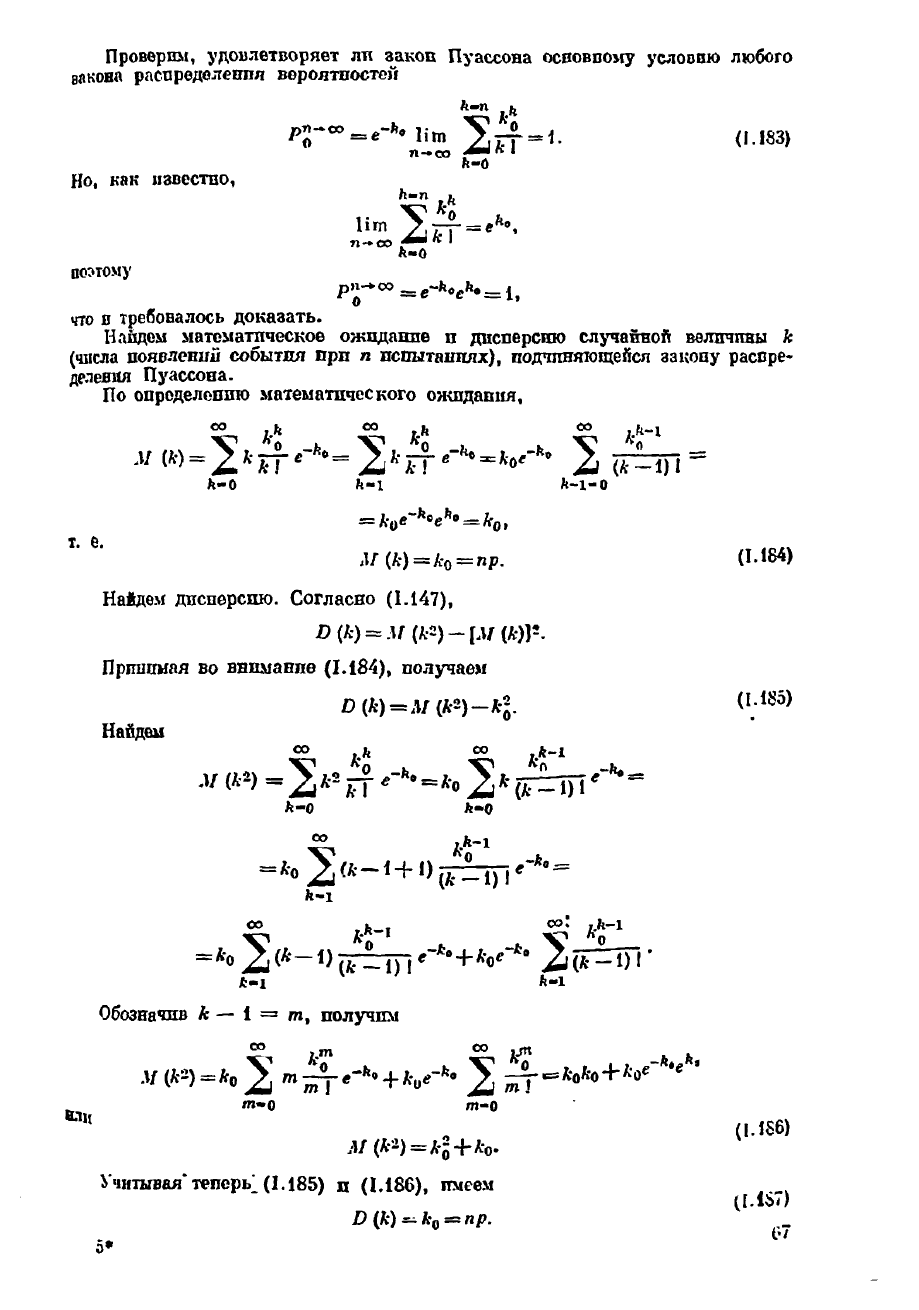
Проверим, удовлетворяет ли заков Пуассона освовпому условию любого

вакова распределения вероятностей

^ к

= (1.183)

п—со '

й-0

Но, как известно,

1!гп

2гг

=ейо

п~со ***

К 1

к-а

поэтому

Р'*-*™ =е~

'е

' = 1,

что и требовалось доказать.

Найдем математическое ожидание п дисперсию случайной величины к

(числа появлений события прп п испытаниях), подчиняющейся закону распре-

деления Пуассона.

По определению математического ожидания,

°° Ь

°° к

л/ Ю =

2 =

к-0 к-1 к-1-0

= к

е-

°е

кв

= к

*' Л/ (к) = ко —пр. (Ы84)

Найдем дисперсию. Согласно (1.147),

П(к) = М (Аг))5.

Принимая во ввпманпе (1.184), получаем

0(А) = Д/(А-2)-*2. (1.185)

Найдем

л/

(к-) = 2 ** кТ

* = 2 * (Т^ТП

к-о к-о

^-о^а-ц-.)^

к-1

=А-0 7/Г~п]

Й-1 Ь-Х

Обозначив к — 1 = т, получим

СО со

тш о т-о

ИЛИ

Учитывая*теперь! (1.185) п (1.186), имеем

(А") — А-

= пр.

(1.186)

([.1Ь7)

Р7

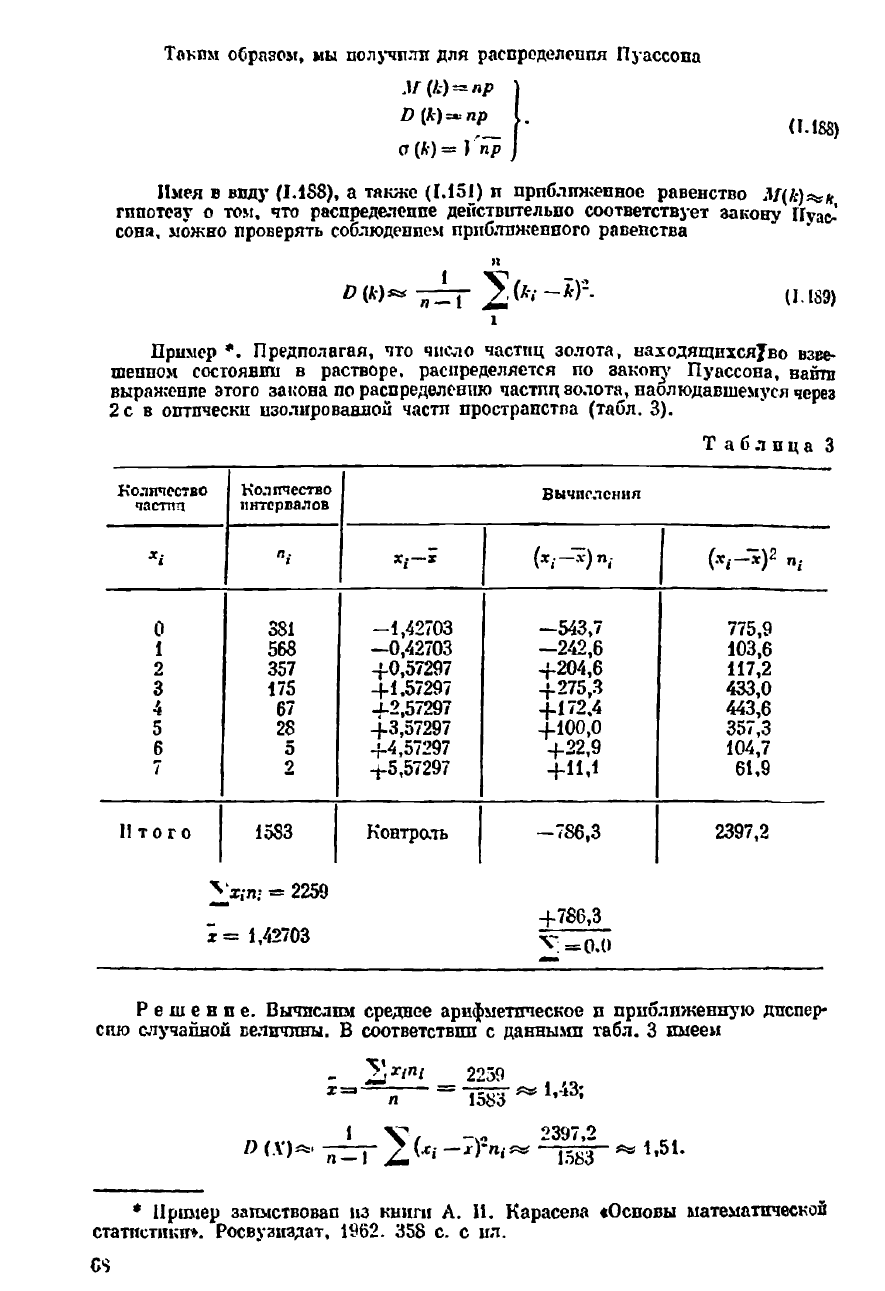
Та к гм образом, мы получили для распроделеппя Пуассопа

ЛГ(к) = *р

ст

(к) = I пр

Имея в виду (1.188), а также (1.151) п приближенное равенство М(к)^н

гппотезу о том, что распределение действительно соответствует закону Пуас-*

соня, можно проверять соблюдением приближенного равенства

-^ТГ -А)

(М89)

Пример Предполагая, что число частиц золота, находящнхся7во взве-

шенном состоявши в растворе, распределяется по закону Пуассона, ваши

выражение этого закона по распределению частпцволота, наолюдавшемуся через

2 с в оптически изолированной части пространства (табл. 3).

Таблица 3

Количество

Вычисления

частиц

интервалов

Вычисления

х,—х

(«I-»)

»,

381

-1,42703

-543,7

775,9

568

-0,42703 -242,6

103,6

357

4-0,57297

+204,6

117,2

175 +1,57297

+275,3

433,0

4 67

4-2,57297

+172.4

443,6

+3,57297

+100,0

357,3

6 5

+4,57297

+22,9

104,7

+5,57297

+11,*

61,9

Итого 1583

Контроль -786,3

2397,2

2259

х= 1,42703

+786,3

^ =0.0

Р е ш е н п е. Вычислим среднее арифметическое и приближенную диспер-

сию случайной величины. В соответствии с данными табл. 3 пмеем

_ 2

'"' 2259

— = 1583

1 - о 2397,2

№)**> " 1583 ^

1,5

* Пример заимствован из книги А. 11. Карасева «Основы математической

статистики». Росвузиздат, 1962. 358 с. с ил.

С*

Довольно хорошее совпадение х п приближенного значения дисперсии

л(Л'). равных 1.43 н 1,51 соответственно, подтверждает предположение о нали-

чии распределения „Пуассона. Выражение для закона Пуассона в данном слу-

чае примет вид

/*(А' = *) = - ^ (1.190)

где

А' =®

0» • • • — возможное количество частиц золотя, находящихся во

взвешенном состоянии в растворе, наблюдавшееся чорк» 2 с в оптически изолиро-

ванной частп пространства. По формуле (1.190) можно вычислить вероятность

для заданного числа к. Таблицу распределения Пуассона см. в прял. 4.

§ 16. ПОНЯТИЕ О МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЯХ

СИСТЕМ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

Систему случайных велпчпн можно понимать как совокупность п случайных

величин, определяющих собой случайное положение точки в п-мерном про-

странстве. В частности, двухмерная система определяет случайное положение

точки на плоскости, трехмерная — в пространстве (папример, место разрыва

сваряда на земле или точка разрыва зенитного снаряда в воздухе).

Приведем без доказательства следующую теорему:

Плотность распределения спстемы независимых

случайных величин равна произведению плотностей

распределения отдельных величия, входящих в си-

стем у.

Предположим, что плотности распределения (т. е. ординаты кривых рас-

пределения) независимых случайных величин X, У, 2, V есть (х), /

(у), /

(г),

/, (и). Тогда плотпость распределения спстемы

/ (г, у. г, и) = Д (х) и (у) /

(^ /, <«). (1.191)

Вероятность попадания в окрестность точки К (х, у, и)

=к И /

(У) /з (=) /4 (и)

<** Лу

й* йи. (1.192)

Вероятность попадания в область вычисляют по формуле

Ра = (Ш /, И и (у)

Ы (*)

и («) ** ду ё: ди. (1.193)

Для'двухмерного нормального распределения вероятность попадания точка

в прямоугольник со сторонами, параллельными осям координат, равна

5, о<_т, о(г>

*'Л\=ТС } )

5./о (А-)ч, с (V)

где

л; щ=У1—У.

При трехмерном нормальном распределении вероятность попадания точки

параллелепипед^ гранями, параллельными координатным плоскостям, равна

*.. У., г, - л'-'

3 3 3 « " Л^ЛуЛг.

4./О Шт.,.

(Г)5,/о (2)

где

; . ч .

Х^С(Х)' 'г—а (У)*

г-а(Х)*

А'; Ч^'л—У; = —

Для вычисления вероятности попадания точки в задаииую область произ-

вольной формы па плоскоспг пли в ааданпую прострапственпую область должны

быть известны грашщы этих областей в виде соответствующих уравнений.

Тогда придется вычислять кратные пптегралы с переменными границам пзме-

нений пределов интегрирования.

Прп равномерном законе распределения вероятностей у всех аргументов

вероятность попадания точки в область пропорциональна площади этой области

прп двухмерном распределении и пропорциональна объему — прп трехмерном.

Случай завпагмых случайных величин п комбинации разных распределений

рассматривать не будем.

§ 17. ПРЕДЕЛЬНЫЕ ЗАКОНЫ

1. Закон больших чисел

Теория вероятностей основывается на .математической интерпре-

тации реальных свойств массовых случай пых явлений или, как гово-

рят, статистических закономерностей. Одним из важнейших математи-

ческих выражений этих закономерностей является закон болыипх

чисел. Согласно этому закону, среднее значение случайной величины

с увеличением числа наблюдений сходится по вероятности к матема-

тическому ожиданию. В такой формулировке закоп больших чисел

называют теоремой Чебышева. В виде формулы эта тео-

рема выглядит так:

Р (1*-*|<е)>1-б, (1.196)

Л-+00

где

и б — сколь угодно малые положительные числа.

В частности, имея в виду, что М — Р> получаем теорему

Бернулли

^(т)--Р 1<гМ >1-6, (М97)

Л-»со

/ I I

где Л' — число серий испытаний, в каждой пз которых выполнено

п опытов.

Теорем}' Чебышева доказывают па основе следующего неравенства Чебы-

шева:

Р(1*-Х1>*)<~!Г' (1.198)

где а — любое положительное копечпое число.

Докажем справедливость неравенства (1.198)

Х-О. +СО

*-А'

«)= | / (х) йх + | / (х) (1х, (1.13»

Хм

где / (я) — плотность распределения вероятностен случайпой величины.

7о

Далее имеем

+со _ А'-а

-00 -со

+ 00

+ \х-Х\

-Цх)<1х. (1.200)

ЛЧа

Заменяя переменную величину | х — X | ое нижним пределом а, мы усилим

неравенство (1.200). Поэтому

О (.V) > «2 | / (г) ах-Ьаг | / (г)

<1х

Х+а

Х-ч +оо |

I 1(х)(1х+ ^ 1(х)Ц,

° Х+а )

или. принимая во внимание (1.199),

»(Х) >«2/>(|*-А|>СО.

откуда получается неравенство (1.198).

Заменяя везде знак интеграла знаком7суммы, а / (х) Ах — соответствую

щими значениями вероятностен, легко доказать справедливость неравенства

Чебышева для дискретных случайных величин. Заметим, что неравенство Чебы-

шева указывает лншь верхшою границу вероятностп'отклонения | х — X | на за-

данвую положительную величину а при любом законе распределения. Если же

«акоп распределения известен, то вероятность отклонения | х — Х| молшо оце-

нить более точно.

Рассмотрим следующую задачу.

Известны случайная величина А' и ее основные характеристики:

М (X) и В (X). Произведено п наблюдений и получено п значений

(

(* — 1. . . ., п).) Из п значении X взято среднее арифметическое

х. В свою очередь, полученное значение х .может рассматриваться

как одно из значений некоторой случайной величины У, причем со-

вокупность значений этой случайной величины есть всевозможные

средние арифметические значения в разных сериях наблюдении,

в каждой из которых произведено п наблюдений. Требуется найти

основные характеристики случайной величины т. е.

М (У) и О (У).

Будем рассуждать так: наблюденные значения А* можно рассмат-

ривать как результаты наблюдении п независимых случанпых вели-

чин X,, X.,. Х

, . . Х„, имеющих одинаковые характеристики: X

и Ю (X).

Тогда

У = 4"

(А

'* +

А'А

• • + А',..), (1.201)

т. е. V можно рассматривать как среднее арифметическое одинаково

распределенных взаимно независимых случайных величии. Пп основа-

нии (1.201) сразу получаем

Но по условию Х, = А'

= ...= А'„ --= А', поэтому

т. е.

(1.202)

Найдем дисперсию В {>") = О (ж), пользуясь тем, что постоян-

ный множитель можно вцнести за знак дисперсии, возведя его в квад-

рат.

0{У) = 0(х) = 0

1-1

г Н 1

(1.203)

Учитывая, что рассматриваемые величины одинаково распреде-

лены, т.е.Б (а-,) = /) (г.,) = ... = Б (а:

) = В (;г), а также свойство

дисперсии

получаем *

«-1

-"[(1ЧИТ-

Принш1ая во внимание, что X; = X = сопз{, и пользуясь свойствами ма-

тематического ожидания, нашппем

=л/12; (х,-*>»+ 2 2 & - х) (ч

$>«]+

1»-1 1-1 1-1 I 1-1

I 2

Л/

(И-Х) М (Х]-Х) = 2

(*).

«-1 /-1 |-1

так как М (я, — X) = 0, окончательно получим

-л/) (А').