Богатиков А.Н., Красицкий В.А., Лапков К.Н. и др. Сборник задач, вопросов и упражнений по общей неорганической химии
Подождите немного. Документ загружается.


41
dhc J_Zdpby ijhl_dZxsZy k ih]ehs_gb_f l_iehluQ < l _ k ih-
\ur_gb_fwglZevibbkbkl_fuûH > gZau\Z_lkywg^hl_jfbq_kdhc.
Hkgh\gufaZdhghfl_jfhobfbby\ey_lkyaZdhg=_kkZ
l_ieh
\hcwnn_dlj_Zdpbbhij_^_ey_lkylhevdhgZqZevgufbdhg_qgufkh
klhygb_fkbkl_fubg_aZ\bkblhlimlbi_j_oh^Zkbkl_fubah^gh
]hkhklhygby\^jm]h_.
Ke_^kl\b_baaZdhgZ =_kkZ
klZg^Zjlgucl_ieh\hcwnn_dlj_
ZdpbbjZ\_gkmff_klZg^Zjlguol_iehlh[jZah\Zgbyijh^mdlh\j_
Zdpbb aZ \uq_lhf kmffu klZg^Zjlguo l_iehl h[jZah\Zgby bkoh^
guo\_s_kl\kmq_lhfkl_obhf_ljbq_kdbodhwnnbpb_glh\
∆
G
0
298
j-pbb
∑∆
f
G
0
298
ijh^–
∑∆
f
G
0
298
bko
Ijbf_j
Ihevamykv ^Zggufb h klZg^Zjlguo wglZevibyo h[jZ
ah\Zgby\_s_kl\\j_Zdpbb0J
+ CO = 2MgO + C \uqbk
eblv
∆
G
j_Zdpbb
J_r_gb_
Bkoh^ybalZ[ebqguo^ZgguoihwglZevibyfh[jZah\Zgby&2
2
b
0J2 b mqblu\Zy qlh klZg^Zjlgu_ wglZevibb h[jZah\Zgby \_s_kl\
jZ\gugmexgZoh^bf\_ebqbgmklZg^ZjlghcwglZevibbj_Zdpbb
∆
G
0
298
=2
∆
f
G
0
298
(MgO) –
∆
f
G
0
298
(CO
2
) =
= –601,8
.
2 + 393,5 = –d>`fhev
Ijbf_j
Bkoh^y ba l_iehlu h[jZah\Zgby ]Zahh[jZagh]h ^bhd
kb^Zm]e_jh^Z&2
2
) = –d>`fhevbl_jfhobfbq_kdh]hmjZ\g_
gbyK
+ 2N
2
O KH + 2N ;
∆
G
0
298
= –d>`<uqbkeblv
l_iehlmh[jZah\Zgby1
2
O .
J_r_gb_
∆
G
0
298
j-pbb
∆
f
G
0
298
(CO
2
) + 0) – (2
∆
f
G
0
298
(N
2
O) + 0),
hldm^Z
2
∆
f
G
0
298
(N
2
O) =
∆
f
G
0
298
(CO
2
) –
∆
G
0
298
j-pbb
–393,5 – (– d>`
Ke_^h\Zl_evgh
∆
f
G
0
298
(N
2
2 d>`fhev
GZijZ\e_gb_\dhlhjhfkZfhijhba\hevghijhl_dZ_lobfbq_kdZy
j_Zdpbyhij_^_ey_lkykh\f_klguf^_ckl\b_f^\monZdlhjh\l_g
^_gpb_c d i_j_oh^m kbkl_fu \ khklhygb_ k gZbf_gvr_c \gmlj_gg_c
wg_j]b_c\kemqZ_bah[Zjguoijhp_kkh\
–
kgZbf_gvr_cwglZevib_c
l_g^_gpb_c d^hklb`_gbx gZb[he__ \_jhylgh]h khklhygby l _
khklhygby dhlhjh_ fh`_l [ulv j_Zebah\Zgh gZb[hevrbf qbkehf
jZ\gh\_jhylguokihkh[h\fbdjhkhklhygbc

42
F_jhci_j\hcbawlbol_g^_gpbc^eybah[Zjguoijhp_kkh\kem
`blbaf_g_gb_wglZevibb\obfbq_kdhcj_ZdpbbhljbpZl_evgucagZd
∆
GmdZau\Z_lgZmf_gvr_gb_Ziheh`bl_evguc–gZ\hajZklZgb_wg
lZevibbkbkl_fu
F_jhc \_jhylghklbg_mihjy^hq_gghklb [_kihjy^dZ khklhygby
kbkl_fu \ l_jfh^bgZfbd_ ijbgylh kqblZlv wgljhibx S – \_ebqbgm
ijhihjpbhgZevgmx eh]Zjbnfm qbkeZ jZ\gh\_jhylguo fbdjhkhklhy
gbcq_j_adhlhju_fh`_l[ulvj_Zebah\Zgh^Zggh_fZdjhkhklhygb_
S = k
.
ln W.
?^bgbpZbaf_j_gbywgljhibb–>`fhevÜK.
Wgljhiby\hajZklZ_lijbi_j_oh^_\_s_kl\ZbadjbklZeebq_kdh]h
khklhygby \ `b^dh_ b ba `b^dh]h \ ]Zahh[jZagh_ ijb jZkl\hj_gbb
djbklZeeh\ijbjZkrbj_gbb]Zah\ijbobfbq_kdbo\aZbfh^_ckl\byo
ijb\h^ysbodm\_ebq_gbxqbkeZqZklbpbij_`^_\k_]hqZklbp\]Z
ahh[jZaghfkhklhygbbGZijhlb\\k_ijhp_kku\j_amevlZl_dhlhjuo
mihjy^hq_gghklv kbkl_fu \hajZklZ_ldhg^_gkZpby ihebf_jbaZpby
k`Zlb_ mf_gvr_gb_ qbkeZ qZklbp khijh\h`^Zxlky mf_gvr_gb_f
wgljhibb
Ijbf_j
G_ijhba\h^y\uqbke_gbchij_^_eblvagZdbaf_g_gby
wgljhibb\ke_^mxsboj_Zdpbyo
NH
4
NO = N
2
O G
2
H ; (1)
G
H G
2
H ; (2)
G
H G
2
H . (3)
J_r_gb_
<j_Zdpbbfhev\_s_kl\Z\djbklZeebq_kdhfkhklhygbbh[
jZam_lfhev ]Zah\ ke_^h\Zl_evgh ûS
1
> < j_Zdpbyob
mf_gvrZ_lkydZdh[s__qbkehfhe_clZdbqbkehfhe_c]Zahh[jZaguo
\_s_kl\lZdqlhûS
2
< bûS
3
< IjbwlhfûS
3
bf__l[he__hljbpZ
l_evgh_agZq_gb_q_fûS
2
lZddZdS(H
2
O ) < S(H
2
O ).
>ey wgljhibb kijZ\_^eb\h ml\_j`^_gb_ ZgZeh]bqgh_ jZkkfhl
j_gghfm \ur_ ^ey
∆
G: baf_g_gb_ wgljhibb kbkl_fu \ j_amevlZl_
obfbq_kdhcj_Zdpbb
∆
6jZ\ghkmff_wgljhibcijh^mdlh\j_ZdpbbaZ
\uq_lhfkmffuwgljhibcbkoh^guo\_s_kl\DZdbijb\uqbke_gbb
wglZevibbkmffbjh\Zgb_ijhba\h^ylkmq_lhfkl_obhf_ljbq_kdbodh
wnnbpb_glh\
KlZg^ZjlgZywgljhibyijhkluo\_s_kl\\hlebqb_hlwglZev-
ibbh[jZah\Zgbyijhkluo\_s_kl\g_jZ\gZgmex
43
Nmgdpb_ckhklhygbyh^gh\j_f_gghhljZ`Zxs_c\ebygb_h[_bo
mihfygmluo\ur_l_g^_gpbcgZgZijZ\e_gb_ijhl_dZgbyobfbq_kdbo
ijhp_kkh\ kem`bl wg_j]by =b[[kZ (k\h[h^gZy wg_j]by k\yaZggZy k
wglZevib_cbwgljhib_ckhhlghr_gb_f
G = H – TS,
]^_L –Z[khexlgZyl_fi_jZlmjZ
DZd \b^gh wg_j]by =b[[kZ bf__l lm `_ jZaf_jghklv qlh b wg
lZevibybihwlhfmh[uqgh\ujZ`Z_lky\>`bebd>`
>eybah[Zjgh-bahl_jfbq_kdboijhp_kkh\l_ijhp_kkh\ijhl_
dZxsboijbihklhygguol_fi_jZlmj_b^Z\e_gbbbaf_g_gb_wg_j]bb
=b[[kZjZ\gh
∆
G =
∆
H – T
∆
S.
DZdb\kemqZ_
∆
Hb
∆
S, baf_g_gb_wg_j]bb=b[[kZ
∆
G \j_amev
lZl_ obfbq_kdhc j_Zdpbb (wg_j]by =b[[kZ j_Zdpbb jZ\gh kmff_
wg_j]bc =b[[kZ h[jZah\Zgby ijh^mdlh\ j_Zdpbb aZ \uq_lhf kmffu
wg_j]bc=b[[kZh[jZah\Zgbybkoh^guo\_s_kl\kmffbjh\Zgb_ijhba
\h^ylkmq_lhfqbkeZfhe_cmqZkl\mxsbo\j_Zdpbb\_s_kl\
Wg_j]bx =b[[kZ h[jZah\Zgby \_s_kl\Z hlghkyl dfhex wlh]h
\_s_kl\Zbh[uqgh\ujZ`Zxl\d>`fhevijbwlhf
∆
G
0
h[jZah\Zgby
gZb[he__ mklhcqb\hc fh^bnbdZpbb ijhklh]h \_s_kl\Z ijbgbfZxl
jZ\ghcgmex.
Ijbihklhygkl\_l_fi_jZlmjub^Z\e_gbyobfbq_kdb_j_Zdpbbfh-
]mlkZfhijhba\hevghijhl_dZlvlhevdh\lZdhfgZijZ\e_gbbijbdhlh-
jhf
wg_j]by=b[[kZkbkl_fumf_gvrZ_lky
∆
G
<
0)
Wlh_klvmkeh\b_
ijbgpbibZevghc\hafh`ghklbhkms_kl\e_gby^Zggh]hijhp_kkZ
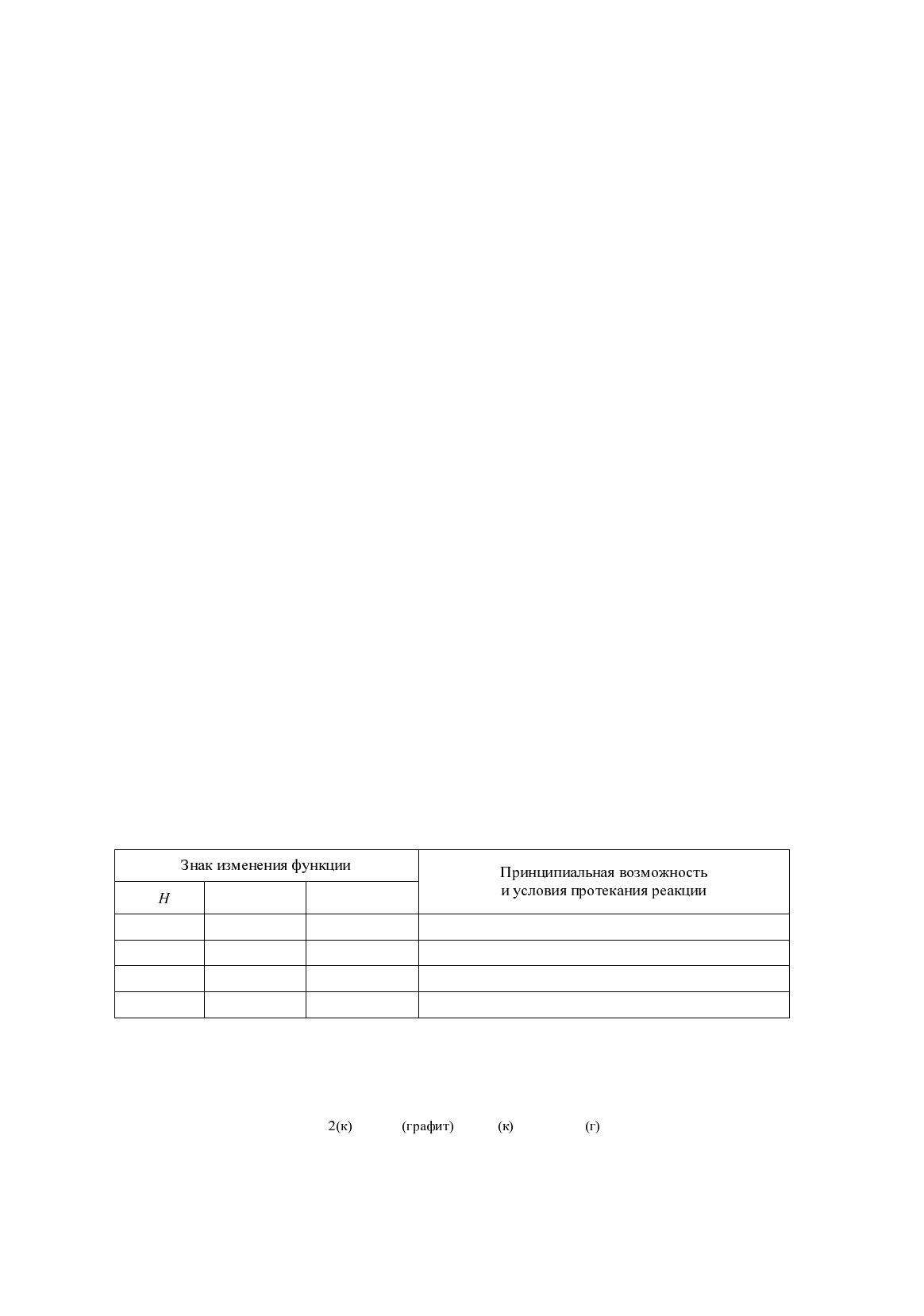
< ijb\_^_gghc lZ[ebp_ihdZaZgZ \hafh`ghklv bmkeh\byijhl_
dZgbyj_ZdpbbijbjZaebqguokhq_lZgbyoagZdh\
∆
Gb
∆
S.
∆
∆
S
∆
G
– + –
<hafh`gZijbex[hcl_fi_jZlmj_
+ – +
IjbgpbibZevghg_\hafh`gZ
– – ±
<hafh`gZijbgbadbol_fi_jZlmjZo
+ + ±
<hafh`gZijb\ukhdbol_fi_jZlmjZo
Ijbf_j
.
Ihevamykv kijZ\hqgufb ^Zggufb mklZgh\blv \ha
fh`ghebijbl_fi_jZlmjZobD\hkklZgh\e_gb_hdkb^ZlblZ
gZ,9^hk\h[h^gh]hf_lZeeZihko_f_
TiO
K
= Ti
KH
?

44
AZ\bkbfhklvx
∆
G
b
∆
S hll_fi_jZlmjuij_g_[j_qv
J_r_gb_
AgZq_gbyûG
0
\d>`fhevijbD^eyTiO
2
(–bCH
(–Lh]^Z^eyjZkkfZljb\Z_fhcj_ZdpbbûG
0
298
= –137,1·2 – (–888,6) =
d>`IhkdhevdmûG
0
298
!\hkklZgh\e_gb_TiO
2
ijbDg_
\hafh`gh
>eyjZkq_lZûG
0
2500
\hkihevam_fkymjZ\g_gb_fûG = ûH
o
– TûS
o
.
Ijb wlhf \khhl\_lkl\bb k mdZaZgb_f\ mkeh\bb aZ^Zqb bkihevam_f
agZq_gbyûG
bûS
o
ijbD>eyjZkq_lZûH
o
bûS
o
j_Zdpbcg_h[oh
^bfhgZclb\lZ[ebp_agZq_gbyûG
0
^eyTiO
2
(–bKH–110,5),
ZlZd`_agZq_gbyS
o
^eyTiO
2
KTibKH
Lh]^Z^eyjZkkfZljb\Z_fhcj_Zdpbb
ûH
o
= –110,5 · 2 – (– d>`
ûS
o
= 30,6 + 197,5 · 2 – 50,3 – 5,7 · 2 = –>`D
L_i_jvgZoh^bfûG
0
2500
j_Zdpbb\ujZ`ZyûS
o
\d>`D
ûG
0
2500
= ûG
0
2500
– TûS
0
2500
= 722,9 – 2500 · 363,9/1000 =
= 722,9 – 909,8 = –d>`
LZdbf h[jZahf ûG
0
2500
< lZd qlh \hkklZgh\e_gb_ TiO
2
]jZnb
lhfijbD\hafh`gh
<hijhku^eykZfhklhyl_evghcih^]hlh\db
1. >Zcl_ hij_^_e_gb_ ihgylbyf kbkl_fZ nZaZ kj_^Z fZdjh- b
fbdjhkhklhygb_.
2. DZdb_kbkl_fugZau\Zxlky]hfh]_ggufbZdZdb_–]_l_jh]_ggufb"
3. DZdb_^\ZnZdlhjZhij_^_eyxlkZfhijhba\hevgh_ijhl_dZgb_ob
fbq_kdboj_Zdpbc\^ZgghfgZijZ\e_gbb"
4. GZah\bl_ hkgh\gu_ l_jfh^bgZfbq_kdb_ \_ebqbgu oZjZdl_jb
amxsb_khklhygb_kbkl_fuIhq_fmhgbghkylgZa\Zgb_nmgdpbc
khklhygby?
5. JZkkfhljbl_ kfuke ihgylbc \gmlj_ggyy wg_j]by kbkl_fu b wg
lZeviby Ijb\_^bl_ ijbf_ju j_Zdpbc m dhlhjuo
∆
Η
>
∆
U b
∆
U
>
∆
Η
.
6. DZdb_ nZdlhjuhij_^_eyxl\_ebqbgmbaf_g_gbywglZevibbj_Zd
pbb"DZdaZ\bkblwlZ\_ebqbgZhlwg_j]bbZdlb\Zpbbimlbbmkeh
\byijhl_dZgbyijhp_kkZijbkmlkl\bydZlZebaZlhjh\"
45
7. Fh]ml eb [ulv wdahl_jfbqgufb ijhp_kku ^bkkhpbZpbb fhe_dme
gZZlhfubhguwg^hl_jfbqgufb–ijhp_kkuh[jZah\Zgbyfhe_
dmebaZlhfh\jZ^bdZeh\ba^jm]bofhe_dme"
8. H[tykgbl_ kfuke ihgylby wglZeviby h[jZah\Zgby \_s_kl\Z.
Knhjfmebjmcl_ mkeh\by klZg^ZjlbaZpbb wlhc oZjZdl_jbklbdb
Q_fhlebqZxlkyklZg^Zjlgu_mkeh\byhlghjfZevguo"
9. Knhjfmebjmcl_aZdhg=_kkZDZdZyk\yavf_`^ml_ieh\ufwnn_d
lhfwglZevib_c j_Zdpbb b wglZevibyfb h[jZah\Zgby bkoh^guo
\_s_kl\bijh^mdlh\j_Zdpbb"
10. Q_f h[tykgy_lky kZfhijhba\hevgh_ ijhl_dZgb_ g_dhlhjuo j_Zd
pbckih]ehs_gb_fl_ieZ
∆Η>
0)?
11. >Zcl_h[tykg_gb_ihgylbywgljhiby.
12. G_ijh\h^yjZkq_lZ hij_^_ebl_agZdbaf_g_gbywgljhibb\oh^_
ke_^mxsboijhp_kkh\
Z+
2
+ O = 2H
2
O ;
[+
2
S + 3O = 2 H
2
O + 2 SO ;
\ MgO
+ CO = MgCO ;
]e_^
→
\h^Z
→
iZj
^) CH
3
COOH
( - )
= CH
3
COOØ+
+
.
13. >Zcl_hij_^_e_gb_ihgylbywg_j]by=b[[kZ.
14. DZdh\hkhhlghr_gb_f_`^m\_ebqbghcbaf_g_gbywg_j]bb=b[[kZ
b\_ebqbgZfbbaf_g_gbywglZevibbbwgljhibbkbkl_fu"
15. Ihq_fm
∆
Gfh`_ljZkkfZljb\ZlvkydZddjbl_jbckZfhijhba\hev
ghklbijhl_dZgbyobfbq_kdhcj_Zdpbb"<hafh`guebkemqZbdh
]^Zj_Zdpbbk
∆
G
<
ijZdlbq_kdbg_b^ml">Zcl_h[tykg_gb_
16. Mqblu\ZyjhevwglZevibcgh]hbwgljhibcgh]hnZdlhjh\bl_fi_
jZlmju\hij_^_e_gbb\_ebqbgu
∆
G\u^_ebl_q_luj_h[sbolbiZ
j_ZdpbcjZaebqZxsboky\hafh`ghklvxbl_fi_jZlmjgufbmkeh
\byfbijhl_dZgby
AZ^Zqb^eyj_r_gby
106. Qlh gZau\Zxl l_ieh\ufb wnn_dlZfb j_Zdpbc" < dZdbo kemqZyo
mjZ\g_gbyobfbq_kdboj_ZdpbcgZau\Zxll_jfhobfbq_kdbfb"
107. DZdb_mkeh\bykhklhygbykbkl_fuijbgbfZxl\l_jfh^bgZfbd_\
dZq_kl\_klZg^Zjlguo"DZdbfbkbf\heZfbboh[hagZqZxl"
108. QlhgZau\Zxl\gmlj_gg_cwg_j]b_ckbkl_fu"Ihq_fm\l_jfh^b
gZfbq_kdbojZkq_lZobkihevamxlg_Z[khexlgu_agZq_gby\gml
j_gg_c wg_j]bb U Z__ baf_g_gb_
∆
Uijb i_j_oh^_kbkl_fu ba
h^gh]hkhklhygby\^jm]h_"

46
109. DZdbf mjZ\g_gb_fhij_^_ey_lky wglZevibyb __ baf_g_gb_"DZ
dhc aZdhg y\ey_lky hkgh\guf aZdhghf l_jfhobfbb" >Zcl_ _]h
nhjfmebjh\dm
110. DZdhcnmgdpb_ckhklhygbyoZjZdl_jbam_lkyl_g^_gpbykbkl_fud
^hklb`_gbxlZdgZau\Z_fh]hgZb[he__\_jhylgh]hkhklhygbydh
lhjhfm khhl\_lkl\m_l fZdkbfZevgZy [_kihjy^hqghklv jZkij_^_
e_gbyqZklbp"
111. DZdbaf_gy_lkywgljhibykbkl_fukih\ur_gb_fl_fi_jZlmju\
j_Zdpbyokbgl_aZbjZaeh`_gby\_s_kl\"
112. DZd baf_gy_lky wgljhiby kbkl_fuijbbkiZj_gbb dhg^_gkZpbb
m\_ebq_gbb^Z\e_gbynZah\uoi_j_oh^Zo"
113. DZdbfb h^gh\j_f_ggh ^_ckl\mxsbfb nZdlhjZfb hij_^_ey_lky
gZijZ\e_gghklvobfbq_kdh]hijhp_kkZ"
114. Ijbkh_^bg_gbb]`_e_aZkk_jhc\u^_ebehkvd>`JZk
kqblZlvl_iehlmh[jZah\Zgbykmevnb^Z`_e_aZ
115. Hij_^_eblv klZg^Zjlgmx wglZevibx
∆
G
0
298
h[jZah\Zgby JG
3
,
bkoh^ybamjZ\g_gby
2PH
H J
2
H G
2
H
;
∆
G
= –d>`
116. Bkoh^ybal_ieh\h]hwnn_dlZj_Zdpbb
KZH
J
2
H KZ
3
JH
4
) ;
∆
G = –d>`
hij_^_eblv
∆
G
0
298
h[jZah\ZgbyhjlhnhknZlZdZevpby
117. KjZ\gblv
∆
G
0
298
j_Zdpbb\hkklZgh\e_gbyhdkb^Z`_e_aZIIIjZa
ebqgufb\hkklZgh\bl_eyfbijbD
Z)H
2
O + 3H
2
= 2 Fe + 3H
2
O ;
[)H
2
O K = 2 Fe KH ;
\)H
2
O KH = 2 Fe KH .
118. <uqbkeblvagZq_gb_
∆
G
^eyijhl_dZxsbo\hj]Zgbaf_j_Zdpbc
ij_\jZs_gby]exdhau
ZK
6
G
12
H K
2
G
5
HG KH
;
[K
6
G
12
H H KH G
2
H
.
DZdZybawlboj_ZdpbcihklZ\ey_lhj]Zgbafm[hevr_wg_j]bb"
119.
G_ ijhba\h^y \uqbke_gbc mklZgh\blv agZd
∆
S
ke_^mxsbo
ijhp_kkh\
Z1+
= N + 3H ;
[KH
KH
;
\12
+ O = 2NO ;
]+
2
S + 3O = 2H
2
O + 2SO ;
^K+
3
OH + 3O = 4H
2
O
KH
.

47
120. G_ijhba\h^y\uqbke_gbcmdZaZlv^eydZdbobai_j_qbke_gguo
ijhp_kkh\baf_g_gb_wgljhibbiheh`bl_evgh
Z0J2
+ H = Mg + H
2
O ;
[K
KH KH ;
\KG
3
KHHG KG
3
KHH
-
G
+
;
]G&O
H
= 2Cl
G
2
H
;
^1+
4
NO = N
2
O
)
G
2
H
.
121.
MklZgh\blv ijhl_dZgb_ dZdbo ba gb`_ke_^mxsbo j_Zdpbc \ha
fh`gh\klZg^Zjlguomkeh\byo
Z1
+ ½
H
= N
2
O ;
[+&O
H
= 2Cl
G
2
H
;
\)H
2
O
KH
= 2Fe
KH
.
122.
MdZaZlvdZdb_baj_Zdpbch[jZah\Zgbyhdkb^h\ZahlZbijbdZdbo
l_fi_jZlmjZo\ukhdbobebgbadbofh]mlijhl_dZlvkZfhijhba
\hevgh
Z1
H
= 2N
2
O ;
∆
G
298
> 0
[1
H
= 2NO ;
∆
G
298
> 0
\12
+ O = 2NO ;
∆
G
298
< 0
]12
+ NO = N
2
O ;
∆
G
298
< 0
123.
Hij_^_ebl_agZq_gby
∆
G
298
,
∆Η
298
b
∆
S
298
^eygb`_ijb\_^_gguo
j_ZdpbcbmklZgh\bl_l_fi_jZlmjgu_mkeh\bybohkms_kl\e_gby
\ijyfhfgZijZ\e_gbb
Z1L2
+Pb =Ni + PbO ;
[1+
= 3H + N ;
\&D&2
= CaO
KH
.
124.
Ih baf_g_gbx klZg^Zjlghc wglZevibb b wgljZibb j_Zdpbb \u
qbkeblvbaf_g_gb_wg_j]bb=b[[kZ
H
+ F = 2HF
125.
Hp_gblv l_jfh^bgZfbq_kdmx \hafh`ghklv ijhl_dZgby \ klZg
^Zjlguomkeh\byoj_Zdpbb
N
+ 2H
2
O = NH
4
NO .
126.
Bkihevamy kijZ\hqgu_ ^Zggu_ hij_^_eblv dZdZy ba j_Zdpbc
l_jfh^bgZfbq_kdb\hafh`gZ\klZg^Zjlguomkeh\byo
a) CaCO
3( )
= CaO
( )
+ CO
2( )
;
[
) CO
2( )
+ CaO
( )
= CaCO
3( )
;
\
) Ca(OH)
2( )
+ CO
2( )
= CaCO
3( )
+ H
2
O
( )
.
127.
Hp_gblv ijbgpbibZevgmx \hafh`ghklv hkms_kl\e_gby j_Zdpbb
f_`^mdhfihg_glZfb Zlfhkn_juZ ijbklZg^Zjlguo mkeh\byo
[ijbih\ur_gghcl_fi_jZlmj_
1) N
+ O
:
NO ; NO ;
2) N
2( )
+H
2
O
( )
:1+
4
NO
2( )
;
3) N
2( )
+ H
2
O
( )
+ O
2( )
:1+
4
NO
3( )
;
4) N
2( )
+ H
2
O
( )
+ O
2( )
:+12
3( )
.

48
= E : < :
IV
HKGH<UOBFBQ?KDHCDBG?LBDB
OBFBQ?KDH?J:<GH<?KB?
NZdlhju\ebyxsb_gZkdhjhklvobfbq_kdhcj_Zdpbb
Kdhjhklv ]hfh]_gghc j_Zdpbb – wlh \_ebqbgZ qbke_ggh jZ\gZy
baf_g_gbxdhgp_gljZpbbh[uqghfheyjghcex[h]hmqZklgbdZj_Zd
pbb\_^bgbpm\j_f_gb
Kj_^gyykdhjhklvj_Zdpbbv
\bgl_j\Ze_\j_f_gbhlt
1
^h t
2
hi
j_^_ey_lkykhhlghr_gb_f
t
c
tt
cc
v
∆
∆
=
−
−
=
1
2
1
2
.
Hkgh\gu_ nZdlhju\ebyxsb_ gZ kdhjhklv ]hfh]_gghcobfbq_
kdhcj_Zdpbb
–
ijbjh^Zj_Z]bjmxsbo\_s_kl\
–
dhgp_gljZpby^Z\e_gb__keb\j_ZdpbbmqZkl\mxl]Zau
–
l_fi_jZlmjZ
–
dZlZebaZlhj
<k_obfbq_kdb_j_ZdpbbihklZ^bcghklbih^jZa^_eyxlkygZwe_
f_glZjgu_ b keh`gu_ ;hevrbgkl\h obfbq_kdbo j_Zdpbc ij_^klZ\
eyxlkh[hckeh`gu_ijhp_kkuijhl_dZxsb_\g_kdhevdhklZ^bcl_
khklhysb_bag_kdhevdbowe_f_glZjguoijhp_kkh\
>ey we_f_glZjguo j_Zdpbc kijZ\_^eb\
aZdhg ^_ckl\mxsbo
fZkk
kdhjhklv we_f_glZjghc obfbq_kdhc j_Zdpbb ijb ^Zgghc l_f
i_jZlmj_ijyfhijhihjpbhgZevgZijhba\_^_gbxdhgp_gljZpbcj_Z]b
jmxsbo\_s_kl\\kl_i_gyojZ\guokl_obhf_ljbq_kdbfdhwnnbpb
_glZf
>eyj_Zdpbb\h[s_f\b^_Z:bB :__kdhjhklvkh]eZkghaZ
dhgm^_ckl\mxsbofZkk\ujZ`Z_lkykhhlghr_gb_f
)
(
)
(
BcAkc
v
ba
=
,
]^_
k:bk<
–
fheyjgu_dhgp_gljZpbbj_Z]bjmxsbo\_s_kl\:b<
k –
dhgklZglZ kdhjhklb ^Zgghc j_Zdpbb Nbabq_kdbc kfuke dhg
klZglu kdhjhklb – hgZ qbke_ggh jZ\gZkdhjhklb obfbq_kdhc j_Zd
pbbijbdhgp_gljZpbyoj_Z]bjmxsbo\_s_kl\F:bF< fheve
DhgklZglZ kdhjhklb ]hfh]_gghc j_Zdpbb aZ\bkbl hl ijbjh^u j_Z]b
jmxsbo\_s_kl\l_fi_jZlmjubdZlZebaZlhjZ
;hevrbgkl\h obfbq_kdbo j_Zdpbc y\eyxlky keh`gufb ijhl_
dZxsbfbq_j_afgh`_kl\hijhf_`mlhqguoklZ^bc<lZdhfkemqZ_aZ
dhg^_ckl\mxsbofZkkijbf_gbflhevdhddZ`^hchl^_evghcklZ^bb

49
>ey]_l_jh]_gguoj_Zdpbc\mjZ\g_gb_aZdhgZ^_ckl\mxsbofZkk
\oh^yldhgp_gljZpbbg_\k_o j_Z]_glh\Zlhevdh
]Zahh[jZaguobeb
jZkl\hj_gguo
LZd ^ey j_Zdpbb ]hj_gby m]ey K
H : KH
mjZ\g_gb_kdhjhklbbf__l\b^
)
O
(
2
ck
v
⋅=
.
Ijbf_j
>eyj_Zdpbb12
+ O <12 ijhl_dZxs_c\
]Zah\hc nZa_ dhgklZglZ kdhjhklb jZ\gZ JZkkqblZcl_ Z gZqZev
gmxkdhjhklvj_Zdpbb_kebbkoh^gu_dhgp_gljZpbb\_s_kl\ jZ\gu
c12 fheve c(O
2
fheve[kdhjhklvwlhcj_Zdpbb\fh
f_gldh]^Zijhj_Z]bjm_l12
J_r_gb_
Z<khhl\_lkl\bbkaZdhghf^_ckl\mxsbofZkkkdhjhklv^Zgghc
j_Zdpbbhibku\Z_lkymjZ\g_gb_f
).
O
(
)
NO
(
2
2
cck
v
⋅⋅=
Ke_^h\Zl_ev-
ghkdhjhklvj_Zdpbb\gZqZevgucfhf_gl\j_f_gb[m^_ljZ\gZ
0384
,
0
3
,
0
4
,
0
8
,
0
2
=⋅⋅=
o
v
fheve
⋅
k
[ Kdhjhklv wlhc j_Zdpbb \ fhf_gl dh]^Zijhj_Z]bjm_l 12
hibku\Z_lky mjZ\g_gb_f
),
O
(
)
NO
(
2
1
2
1
1
cck
v
⋅⋅=
]^_ c
1
12 b c
1
(O
2
) –
gh\u_dhgp_gljZpbb12b2
2
ihke_lh]hdZdijhj_Z]bjh\Zeh12
Bkoh^ybamjZ\g_gbyj_ZdpbbjZkkqblZ_f\_ebqbgu c
1
12b c
1
(O
2
).
12 khklZ\ey_l
∆
c(NO Â fheve lh]^Z
c
1
(NO) = c
0
(NO) –
∆
c(NO) = 0,4 – fheve<khhl\_lkl\bbkh
kl_obhf_ljbq_kdbfb dhwnnbpb_glZfb mjZ\g_gby j_Zdpbb mf_gvr_
gb_dhgp_gljZpbbH
2
jZ\gh
∆
c(O
2
) =
∆
c(NO fheve
LZdbfh[jZahf c
1
H
2
) = c
0
(O
2
) –
∆
c(O
2
) =0,3 – fheveKe_
^h\Zl_evgh
1
v
= 0,8 · 0,3
2
· fheve
⋅
k
Ijbf_j
DZd baf_gblky kdhjhklv j_Zdpbb12
+ Cl <
<12&O
_keb Z m\_ebqblv ^Z\e_gb_\ j_Zdpbhgghf khkm^_\ ^\Z
jZaZ[mf_gvrblvh[t_fkhkm^Z\jZaZ"
J_r_gb_
Z<khhl\_lkl\bbkaZdhghf^_ckl\mxsbofZkkkdhjhklv^Zgghc
j_Zdpbb hibku\Z_lky mjZ\g_gb_f
).
Cl
(
)
NO
(
2
2
cck
v
⋅⋅=
Ihkdhevdm
m\_ebq_gb_ ^Z\e_gby ijb\h^bl d ijhihjpbhgZevghfm m\_ebq_gbx
dhgp_gljZpbc ]Zahh[jZaguo \_s_kl\ dhgp_gljZpbb j_Z]_glh\ \ gh
\uomkeh\byo [m^mljZ\gu c
1
(NO) = 2c
0
(NO), c
1
(Cl
2
) = 2c
0
(Cl
2
Dhg
klZglZ kdhjhklb j_Zdpbb ijb m\_ebq_gbb ^Z\e_gby g_ baf_gy_lky b
kdhjhklvj_Zdpbb\gh\uomkeh\byo[m^_ljZ\gZ
)
Cl
(
)
NO
(
2
1
2
1
1
cck
v
⋅⋅=
=
))
Cl
(
2
(
))
NO
(
2
(
2
0
2
0
cc
k
⋅⋅
=
= 8 · k · c
2
0
(NO) · c
0
(Cl
2
).

50
Hlkx^Zke_^m_lqlh
8
)
Cl
(
)
NO
(
)
Cl
(
)
NO
(
8
2
0
2
0
2
0
2
0
1
=
⋅
⋅⋅⋅
=
cck
cck
v
v
.
Kdhjhklvj_Zdpbbm\_ebqblky\jZa
[ Mf_gvr_gb_ h[t_fZ khkm^Z \jZaZ ijb\h^bl d khhl\_lkl
\mxs_fm m\_ebq_gbx dhgp_gljZpbc j_Z]_glh\ LZdbf h[jZahf
c
2
(NO) = 4 · c
0
(NO), a c
2
(Cl
2
) = 4 · c
0
(Cl
2
J_rZyaZ^ZqmihZgZeh]bbk
ij_^u^msbfimgdlhfihemqbf
64
2
=
v
v
l_mf_gvr_gb_h[t_fZkh
km^Z\jZaZijb\_^_ldm\_ebq_gbxkdhjhklb\jZaZ
<ebygb_l_fi_jZlmjugZkdhjhklvobfbq_kdhcj_Zdpbb
AZ\bkbfhklvkdhjhklbj_Zdpbbhll_fi_jZlmjuijb[eb`_gghhi
j_^_ey_lky wfibjbq_kdbf ijZ\behf <Zgl-=hnnZ ijb ih\ur_gbb
l_fi_jZlmjugZ dZ`^u_ ]jZ^mkh\kdhjhklvobfbq_kdhcj_Zdpbb
m\_ebqb\Z_lky\-jZaZ\jZa
10
1
2
1
2
TT
T
T
v
v
−
γ=
,
]^_
1
2
b
TT
v
v
–
kdhjhklbj_Zdpbbkhhl\_lkl\_gghijbl_fi_jZlmjZoL
2
b
L
1
;
–
l_fi_jZlmjguc dhwnnbpb_gl kdhjhklb j_Zdpbb dhlhjuc \u
qbkey_lky gZhkgh\_ wdki_jbf_glZevguo^Zgguo bijbgbfZ_l agZq_
gby^ey[hevrbgkl\Zj_Zdpbchl^h>ey^Zgghcj_Zdpbb
–
\_eb
qbgZijZdlbq_kdbihklhyggZyijb¨L § 100
.
KihfhsvxijZ\beZ<Zgl-=hnnZ\hafh`ghebrvijbf_jghhp_
gblv\ebygb_l_fi_jZlmjugZkdhjhklvj_Zdpbb;he__lhqgh_hibkZ
gb_ aZ\bkbfhklb kdhjhklb j_Zdpbb hl l_fi_jZlmju hkms_kl\bfh \
jZfdZol_hjbbZdlb\guoklhedgh\_gbc:jj_gbmkZ
< l_hjbb Zdlb\Zpbb \ebygb_ l_fi_jZlmju b dZlZebaZlhjZ gZ
kdhjhklv obfbq_kdhc j_Zdpbb hibku\Z_lky ke_^mxsbf mjZ\g_gb_f
^eydhgklZglukdhjhklbobfbq_kdhcj_Zdpbb
R
T
E
a
Ae
k
−
=
,
]^_:–ihklhyggucfgh`bl_evg_aZ\bkysbchll_fi_jZlmjuhij_
^_eyxsbcky ijbjh^hc j_Z]bjmxsbo\_s_kl\
R
– mgb\_jkZevgZy]Z
ah\ZyihklhyggZy?
–wg_j]byZdlb\Zpbb_–hkgh\Zgb_gZlmjZevgh]h
eh]ZjbnfZDZdke_^m_lbamjZ\g_gby:jj_gbmkZdhgklZglZkdhjhklb
j_Zdpbbl_f[hevr_q_ff_gvr_wg_j]byZdlb\Zpbb
