Blum W., Riegler W., Rolandi L. Particle Detection with Drift Chambers

Подождите немного. Документ загружается.

56 2 The Drift of Electrons and Ions in Gases

We note that the dependence of the drift velocity and the electron energy on E

and N is always through the ratio E/N. This implies that in two gases operated with

different gas pressures and identical temperature, the E ﬁelds must be adjusted in

proportion to the gas pressures in order to obtain identical u and

in both gases.

Reduced ﬁelds are given in units of V cm

−1

Torr

−1

. A special unit has also been

coined: one Townsend (1 Td) is 10

−17

Vcm

In a gas mixture composed of two or more components i with number densities

, the effective cross-section

(

) and the effective fractional energy loss per colli-

sion λ(

) have to be calculated from the properties of the individual components:

(

∑

(

)/N,

λ(

)

(

∑

(

)

(

)/N, (2.21)

N =

∑

The general behaviour of electron drift velocities is that they rise with increasing

electric ﬁeld, then level off or decrease as a result of the combined effects of

(

)

and λ(

) as

increases with increasing E. Examples will be presented in Sect. 2.4

and in Chap. 12.

2.2.2 Drift of Ions

The behaviour of ions differs from that of electrons because of their much larger mass

and their chemical reactions. The monograph by McDaniel and Mason

[MCD 73] deals with the mobility and diffusion of ions in gases in a comprehen-

sive way. Electrons in an electric ﬁeld are accelerated more rapidly than ions, and

they lose very little energy when colliding elastically with the gas atoms. The electron

momentum is randomized in the collisions and is therefore lost, on the average. In

electric ﬁeld strengths that are typical for drift chambers, the electrons reach random

energies far in excess of the energy of the thermal motion, and quite often they surpass

the threshold of inelastic excitation of molecules in the gas. In this case their mobility

becomes a function of the energy loss that is associated with such excitation.

Ions in similar ﬁelds acquire, on one mean-free path, an amount of energy that

is similar to that acquired by electrons. But a good fraction of this energy is lost in

the next collision, and the ion momentum is not randomized as much. Therefore, far

less ﬁeld energy is stored in random motion. As a consequence, the random energy

of ions is mostly thermal, and only a small fraction is due to the ﬁeld. The effect

on the diffusion of ions results in this diffusion being orders of magnitude smaller

than that of electrons in similar ﬁelds. The effect on the mobility is also quite inter-

esting: since the energy scale, over which collision cross-sections vary signiﬁcantly,

is easily covered by the electron random energies reached under various operating

conditions, we ﬁnd rapid and sometimes complicated dependences of electron mo-

bility on such operating conditions – electric and magnetic ﬁeld strengths and gas

composition being examples. In contrast, the mobility of ions does not vary as much.

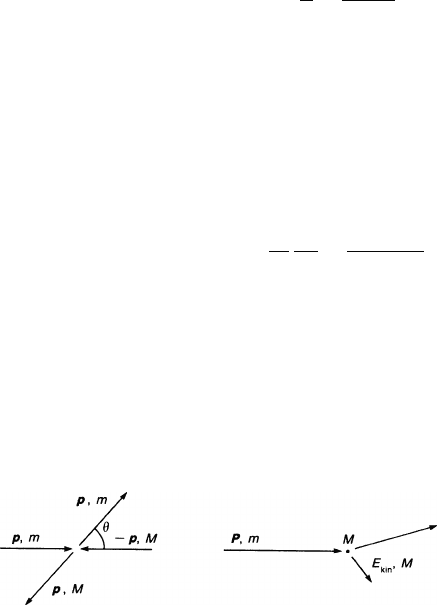
2.2 The Microscopic Picture 57

In order to understand the randomization in more quantitative terms, we consider

the elastic scattering of an ion (or electron) with a molecule of the gas, neglecting

the thermal motion.

Elastic Scattering and the Average Losses of Energy and Momentum. We consider

the scattering of two particles with masses m and M in their centre-of-mass (c.m.)

system in which the incoming momenta are equal and opposite and are denoted by

p. In the laboratory frame, M was initially at rest, and the incoming particle had

momentum P (see Fig. 2.3). The two frames are transformed into each other by the

velocity v

v = P /(M + m).

For elastic scattering, we have |p



| = |p| = M|v

v| = p. The loss of momentum of

particle M along its direction of motion is, in the c.m. system, equal to

p(1−cos

and invariant under the Galilean transformation. At our low momenta the scatter-

ing is isotropic, and after averaging over the angles we ﬁnd the average fractional

momentum loss

M + m

. (2.22)

Similarly, the square of the momentum transfer – equally invariant – is

(p−p



)

= 2p

(1−cos

It is equal to the square of the laboratory momentum of the particle initially at rest;

therefore its kinetic energy is E



kin

= p

(1 −cos

)/M. After averaging over the

angles, the fractional energy loss λ is the ratio of this kinetic energy to that of the

other (incoming) particle in the laboratory system:

λ =

2mM

(M + m)

. (2.23)

We are now in a position to go through the arguments of Sect. 2.2.1 again, apply-

ing them to ions.

Expressions for the Mobility of Ions. Let us consider an ion between two collisions.

Because of its heavy mass it does not scatter isotropically. Immediately after the

collision, superimposed over the random velocity c

there is a component c

in the

drift direction. Some short time later, it has, in addition, picked up the extra velocity

Fig. 2.3 Momentum diagrams for the collision of the drifting particle (mass m) with a gas

molecule (mass M) in the centre of mass and in the rest frame of the molecule

58 2 The Drift of Electrons and Ions in Gases

v equal to the acceleration of the ion along the ﬁeld, multiplied by the average time

that has elapsed since the last collision. The drift velocity is the sum of v and c

u = v

v + c

+ c

. (2.24)

The value of c

is given by the average momentum loss in the direction of the

drift that takes place in the next encounter; it must be equal to the momentum mv

picked up between the encounters:

mc

+ c

v =

m(c

v)=mv

v, (2.25)

where the brackets denote the average over the angles. For the magnitude of c

we calculate c

= v(1 −

, and for the drift velocity (using (2.22)),

u = v + c





. (2.26)

Here

is given by the relative velocity c

rel

between the ion and the gas molecule,

the cross-section

, and the number density N as

= N

rel

. (2.27)

We now distinguish two limiting cases of ﬁeld strength E. If it is low so that the

ion random velocity is thermal, we must take for the relative velocity the average

magnitude of the difference between the two randomly distributed velocities of the

ion (c

ion

) and the gas atoms (c

gas

rel

= |c

ion

−c

gas

| =(c

ions

+ c

gas

)

1/2

. (2.28)

With equipartition of energy, we can express c

rel

through the temperature T and

Boltzmann’s constant k:

rel

= c

ion

+ c

gas

= 3kT





. (2.29)

Using (2.26, 2.27), and (2.29), we obtain

u =





1/2



3kT



1/2

(low E). (2.30)

It is characteristic of the drift velocity at low ﬁelds that it is proportional to E,or

that the mobility is independent of E.

For the case of large E, where we can neglect the thermal motion, we pro-

ceed as in the case of electrons (where the temperature was always neglected). By

combining (2.15, 2.17, 2.24), and (2.26), we solve for u

and c

and obtain the

symmetric forms

2.2 The Microscopic Picture 59

∗



∗



1/2

(2.31)

and

∗



∗



1/2

, (2.32)

where the ‘reduced mass’ m

∗

between the ion (m) and the gas molecule (M) is

deﬁned as

∗

. (2.33)

Using (2.23), we may express λ for elastic scattering through the ratio of the masses,

with the result that

u =





1/2







1/2

(high E). (2.34)

It is characteristic of the drift velocity at high ﬁelds and constant cross-section

that it is proportional to the square root of E, or the mobility decreases as 1/

√

The distinction between ‘high’ and ‘low’ E in (2.30) and (2.34) is obviously with

respect to the ﬁeld in which the ion, over one mean free path, picks up an amount

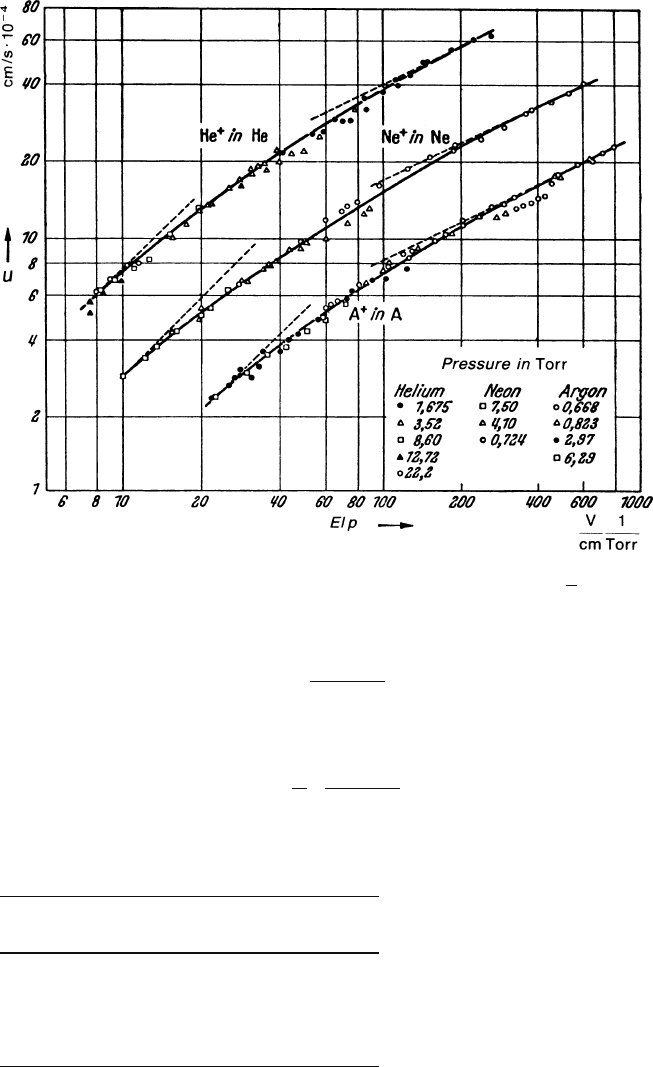
of energy equal to the thermal energy. The measured ion drift velocities for noble

gases shown in Fig. 2.4 exhibit very well the limit in behaviour of (2.30) and (2.34)

with the electric ﬁeld.

Table 2.1 contains ion mobilities for low ﬁelds that were measured in the noble

gases. Various approximation methods for the calculation of cross-sections in the

scattering of ions on molecules have been treated elsewhere [MCD 73]. When ions

travel in their parent gas, the original collision cross-section is increased by about a

factor of two by the mechanism of resonant charge transfer.

Ion Drift in Gas Mixtures. The gas of a drift chamber is often a composition of two

or more constituents. Ion drift in gas mixtures can be understood along the lines of

the last subsection. We want to modify (2.26) for the case where one type of ion

(mass m) moves between the atoms or molecules with masses M

(k = 1, 2,...) each

present in the gas with its own number density N

. The gas number density N is

equal to the sum over all the N

. The resulting drift velocity in the ﬁeld E is called

¯u; it is equal to

¯u =

. (2.35)

Here

is the mean time between collisions, and

is the mean fractional momentum

loss in the mixture; they are both quickly calculated from the

and

that belong

to each constituent. The overall collision rate is the sum of the individual collision

rates, or

∑

(1/

). (2.36)

The overall momentum loss is the average over all the

, weighted with the relative

rates with which each type of molecule is bombarded:

60 2 The Drift of Electrons and Ions in Gases

Fig. 2.4 Drift velocity u of positive noble gas ions in their own gas as functions of the reduced

electric ﬁeld. The limiting behaviour at low ﬁelds (u ∝ E) andathighﬁelds(u ∝

√

E) is visible

[LAN 57]

∑

(

)

∑

(1/

)

. (2.37)

Combining (2.35) to (2.37), we obtain

¯u =

∑

(

)

. (2.38)

Table 2.1 Experimental low-ﬁeld mobilities of various noble gas ions in their parent gas [MCD 73]

Gas Ion Mobility

(cm

−1

)

He He

10.40±0.10

Ne Ne

4.14±0.2

Ar Ar

1.535±0.007

Kr Kr

0.96±0.09

Xe Xe

0.57±0.05

Average over several measurements

2.2 The Microscopic Picture 61

This equation can be cast into a form that is known as Blanc’s law if we denote by

the drift velocity of the ion in the pure component k at the full density N:

, (2.39)

where we have used (2.17). Expressions (2.38) and (2.39) give us Blanc’s law:

¯u

∑

; (2.40)

it states that the inverse drift velocities in the individual gas components add in

proportion to the relative component densities to yield the inverse drift velocity of

the mixture.

Blanc’s law holds for the case of low electric ﬁelds. The case of high ﬁelds is

slightly more complicated because the energy partition of the drifting ion into ran-

dom and directed motion must be taken into account. The reader is referred to the

monograph of McDaniel and Mason [MCD 73].

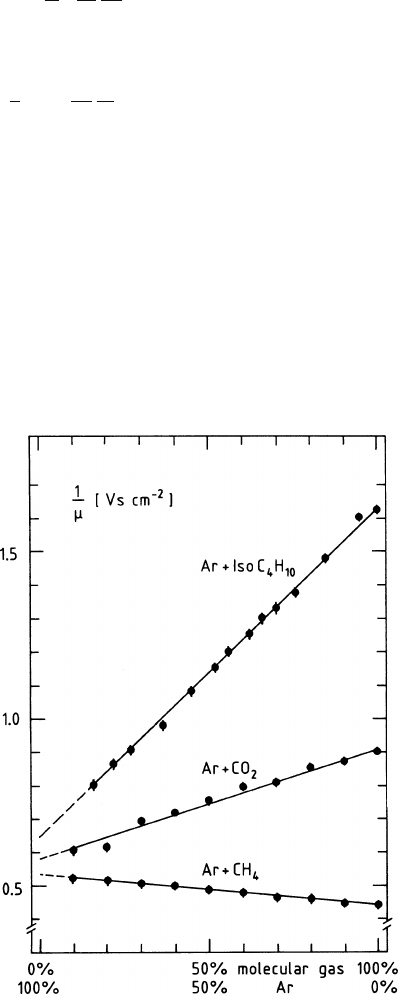
In practice, (2.40) is quite well fulﬁlled. In Fig. 2.5 we show mobilities, mea-

sured by the Charpak group [SCH 77], as functions of the relative gas concentration

for several binary mixtures of argon with the common quench gases: isobutane,

methane, and carbon dioxide.

Fig. 2.5 The inverse of the

mobility of the positive

molecular ions as a func-

tion of the relative volume

concentration of the two com-

ponents in three gas mixture.

Measurements by [SCH 77]

62 2 The Drift of Electrons and Ions in Gases

The production of positive ions in molecular gases is a fairly complex phe-

nomenon, and without a clear identiﬁcation – perhaps using a mass spectrometer –

one is usually ignorant of the identity of the migrating charged bodies. For the pur-

poses of drift chambers it often sufﬁces to know their drift velocities. However, the

chemical deposits on the wire electrodes, as a result of chamber operation, can be

evaluated with more complete knowledge about which ions really migrate toward

the cathodes.

One must read Table 2.2, which contains measured ion mobilities, with these

remarks in mind. For example, the notation ‘[(OCH

)

]

’ means the ion(s) trav-

elling towards the cathode in a mixture of argon + methylal. It is assumed here that

the argon ions that are created simultaneously transfer their charge to the methylal

molecules, thus creating more ‘[(OCH

)

]

’ ions. This is elaborated below.

Charge Transfer. When the migrating ions in a drift chamber collide with molecules

that have an ionization potential smaller than the energy available in the ion, there is

the possibility that a charge-exchange process takes place, which neutralizes the ion

and creates a new ion. This process happens with cross-sections that are of a similar

order of magnitude to the other ion–molecule scattering cross-sections. Therefore

the rate of ion transformation through charge transfer is correspondingly high and

proportional to the concentration of the molecules to be ionized.

The Charpak group have found that 1% of methylal added to binary argon +

isobutane mixtures made a signiﬁcant change in the ion mobility over 2 cm of drift in

their ﬁeld (a few hundred to a thousand V/cm). This has to be interpreted as a charge

transfer process from the ions in the original mixture to the methylal molecules,

thus creating ‘[(OCH

)

]+’ ions with lesser mobility. Their result [SCH 77] is

presented in Fig. 2.6, where the inverse measured mobility is plotted against the den-

sity of the various binary and ternary mixtures. Straight lines correspond to Blanc’s

law; they connect mixtures in which the migrating ion(s) is (are) supposedly the

same. We must therefore imagine the motion of ions in drift chambers as a dynamic

process in which the various ionic species, which were originally produced in the

avalanches or any other collision process, disappear quickly and leave only the one

type that has the lowest ionization potential.

Table 2.2 Measured mobilities of various ions in some gases used in drift chambers [SCH 77]

Ion notation Gas Mobility

(cm

−1

)

[CH

]

Ar 1.87

[CO

]

Ar 1.72

[IsoC

]

Ar 1.56

[(OCH

)

]

Ar 1.51

[CH

]

2.26

[CO

]

1.09

[IsoC

]

IsoC

0.61

[(OCH

)

]

IsoC

0.55

[(OCH

)

]

(OCH

)

0.26

2.2 The Microscopic Picture 63

Fig. 2.6 Inverse mobility of ions in binary and ternary gas mixture composed of

argon–isobutane–methylal, measured by [SCH 77] and plotted as a function of the gas density. A:

argon–methylal; B to E: argon–isobutane–methylal, with argon in different proportions (B: 80%,

C: 70%, D: 60%, and E: 50%) F: argon–isobutane. The numbers close to the experimental points

represent the percentage concentration of methylal (A to E) or isobutane (F), respectively

Practical drift chamber gases – apart from the principal components that were

intentionally mixed together by the experimenter – always contain some impu-

rities; they are difﬁcult to control below the level of 10

−4

. The mere fact that

pulsed lasers of modest energy are capable of producing ionization in ‘clean’ gas

(see Sect. 1.3 for details) is proof of the presence of impurities with low ioniza-

tion potentials. It would obviously be interesting to know the identity of migrating

ions at the end of the 2-m-long drift space of a large time projection chamber

(TPC).

64 2 The Drift of Electrons and Ions in Gases

2.2.3 Inclusion of Magnetic Field

When we consider the inﬂuence of a magnetic ﬁeld on drifting electrons and

ions, the ﬁrst indication may be provided by the value of the mobility

of these

charges. In particle chamber conditions, this is of the order of magnitude of



−1

for electrons (see Fig. 2.17 and use (2.7)), whereas for ions the

order of magnitude is

= 1cm

−1

(see Tables 2.1 and 2.2). Typical magnetic

ﬁelds B available to particle experimenters are limited, so far, by the magnetic sus-

ceptibility of iron, and the order of magnitude is 1 T or 10

−4

Vscm

−2

. We know

from Sect. 2.1 that it is the numerical value of

ωτ

=(e/m)B

that governs the ef-

fects of the magnetic ﬁeld on the drift velocity vector. Using (2.7), which stated that

=(e/m)

, we ﬁnd

ωτ

= B





−4

for ions

1 for electrons

in order of magnitude. Therefore, the effect of such magnetic ﬁelds on ion drift is

negligible, and we concentrate on electrons. This has the advantage that we may

assume that the colliding body scatters isotropically in all directions, owing to its

small mass.

When the magnetic ﬁeld is added to the considerations of Sect. 2.2.1, we can

describe the most general case in a coordinate system in which B is along z, and E

has components E

and E

. An electron between collisions moves according to the

equation of motion,

= eE + e[v

v ×B], (2.41)

which in our case is written as

˙v

= −

˙v

(2.42)

where

≡ (e/m)B and

≡ (e/m)E. Electrons have their direction of motion ran-

domized in each collision, and we are interested in the extra velocity picked up by

the electron since the last collision. Hence we look for the solution of (2.42) with

v = 0att = 0. It is given by

(t)=(

)sin

(t)=(

)(cos

t −1),

(t)=

(2.43)

Before we can identify v with the drift velocity, we must average over t, using (2.16),

the probability distribution of t. This was also done when deriving (2.14), which,

being a linear function of time, required t to be replaced by

, the mean time since

the last collision. The drift velocity for the present case is given by

2.2 The Microscopic Picture 65

= v

(t) =

∞



−t/

sin

t dt =

= v

(t) =

∞



−t/

(cos

t −1)dt =

−

ωτ

, (2.44)

= v

(t) =

∞



−t/

dt =

We immediately recognize that the result is the same as for (2.5) and (2.6), de-

rived from the macroscopic equation of motion using the concept of friction. The

mobility tensor (2.5) is therefore the same in the macroscopic and the microscopic

picture. It will only have to be modiﬁed in Sect. 2.3, where the electron velocity has

a probability distribution over a range of values, rather than a single value.

We can now state the condition of energy balance in the presence of a magnetic

ﬁeld. If the angle between the two ﬁelds is

, the energy transferred to the electron

per unit distance along E, equal to the corresponding collision loss, is

eE =

λmc

(

)

λm

(1+

)

(1+

cos

)

. (2.45)

Here we have used (2.9). On the other hand, the square of the drift velocity was

given by (2.7) and (2.8),





cos

. (2.46)

The two expressions (2.45) and (2.46) determine the two equilibrium velocities u

and c. First we notice that the ratio

(2.47)

is given by the fractional energy loss per collision alone; in particular, it is inde-

pendent of both ﬁelds. In the situation without magnetic ﬁeld, the two electron

velocities were determined by the cross-section and the energy loss in (2.19) and

(2.20). With magnetic ﬁeld, the corresponding relations are more complicated ow-

ing to the presence of the terms proportional to

/(N

). Whereas in

the most general case (2.45) and (2.46) could be solved for c

by a graphical or

numerical method, we present the closed solution for two important practical cases.

Case of E Parallel to B. The ﬁrst case concerns the drift volume of the TPC; here

we have cos

= 1 and therefore



, (2.48)

exactly as in the absence of magnetic ﬁeld.