Blum W., Riegler W., Rolandi L. Particle Detection with Drift Chambers

Подождите немного. Документ загружается.

16 1 Gas Ionization by Charged Particles and by Laser Rays

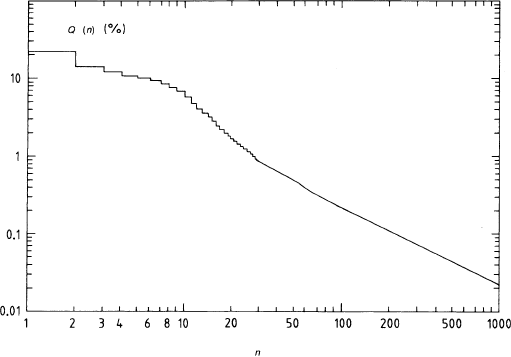
Fig. 1.8 Integral cluster-size distribution for fast particles (

= 1000) in argon; Q(n) is the

probability that the cluster has more than n electrons. Calculated from [LAP 80] and [ERM 77].

For large n, Q(n) ≈ 0.2/n

The quantity p(E, k) contains the details of the various ionization mechanisms de-

scribed in Sect. 1.1 and is generally not known. Lapique and Piuz [LAP 80] have

made a computer model of the atomic processes involved in pure argon and have

thus been able to calculate a cluster-size distribution. It is presented in the integrated

form in Fig. 1.8.

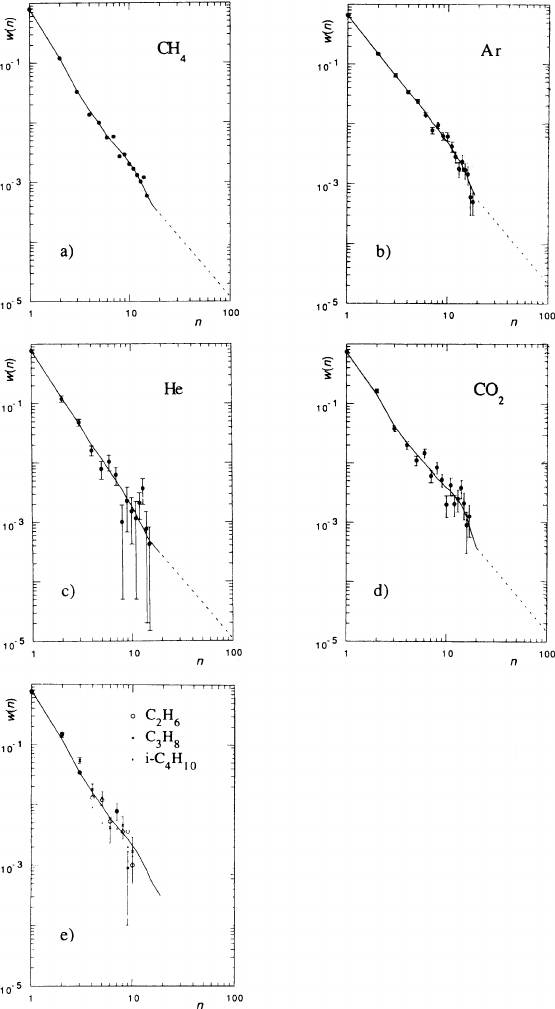
Apart from early cloud chamber studies, there is now one careful experimental

determination of cluster-size distributions from the Heidelberg group [FIS 91]. It

covers the range up to approximately 15 electrons in argon, helium, methane and

several hydrocarbons. We reproduce their measurements in Fig. 1.9. For numeri-

cal applications Table 1.4 contains best estimates for the probabilities P(k), based

on the hand-drawn lines of Fig. 1.9 and their extrapolations according to the 1/n

behaviour expected for unbound electrons.

If one compares these measurements with the calculation of Lapique and Piuz,

then one observes that there is somewhat less structure than they expected in the

function P(k). The Heidelberg group suggest that the absorption of free photons

with its strong energy variation, which is the basis for the model of Chechin et al.

and the PAI model, may not be directly applicable to the calculation of d

/dE.

The number n in these graphs is called k in the text and in Table 1.4.

1.2.5 Ionization Distribution on a Given Track Length

The importance of the cluster-size distribution lies in the fact that, once it is known,

the ionization distribution G(x, n) on the track length x is calculated simply by

summing the cluster size as many times as there are primary encounters in the track

length; G(x, n) depends only on the cluster-size distribution and the number of

1.2 Calculation of Energy Loss 17

Fig. 1.9 Experimental cluster-size distributions from [FIS 91]. The continuous lines are

hand-drawn interpolations whereas the broken lines are extrapolations corresponding to the

1/n

-law expected for large n

18 1 Gas Ionization by Charged Particles and by Laser Rays

Table 1.4 Experimental cluster-size distributions P(k) in per cent by Fischle et al. [FIS 91].

Whereas the measured data and their errors are shown in Fig. 1.9, this table contains interpolated

values for numerical applications. Values in brackets are extrapolations according to the expecta-

tion of free electrons

Ar He CO

178.665.676.60 72.50

212.015.012.50 14.00

33.46.44.60 4.20

41.63.52.02.20

50.95 2.25 1.21.40

60.60 1.55 0.75 1.00

70.44 1.05 0.50 0.75

80.34 0.81 0.36 0.55

90.27 0.61 0.25 0.46

10 0.21 0.49 0.19 0.38

11 0.17 0.39 0.14 0.34

12 0.

13 0.30 0.10 0.28

13 0.10 0.25 0.08 0.24

14 0.08 0.20 0.06 0.20

15 0.06 0.16 0.048 0.16

16 (0.050) 0.12 (0.043) 0.12

17 (0.042) 0.095 (0.038) 0.09

18 (0.037) 0.075 (0.034) (0.064)

19 (0.033) (0.063) (0.030) (0.048)

≥20 (11.9/k

) (21.6/k

) (10.9/k

)(14.9/k

)

clusters. The most practical way to achieve the summation is by the Monte Carlo

method on a computer, especially when the cluster-size distribution exists only in

the form of a table.

In this case, we proceed in two steps. First, we make a random choice from the

Poisson distribution (1.2) of a number m of encounters in the track length x : m =

x/λ. Second, we make m random choices from the cluster-size distribution P(k) of

m cluster sizes k

, k

,..., k

. The number

n =

∑

i=1

(1.36)

is one entry in a frequency distribution G(x, n) of the number of ionization electrons

in x.

Figure 1.10 contains ionization distributions for several track lengths (mean num-

bers m of clusters) in argon that were computed in this way using the integrated

probability Q depicted in Fig. 1.8. The ionization distributions develop a peak that

deﬁnes the most probable ionization I

.Theyalsohaveafull width at half max-

imum W, although the mean and the root-mean-square deviation exist only if an

upper cut-off is introduced. The value of I

is not proportional to the mean number

of clusters but rises from m to ∼3mas mincreases from 5 to 1000. Figure 1.11

1.2 Calculation of Energy Loss 19

Fig. 1.10 Ionization distri-

bution obtained by summing

m times the cluster-size dis-

tribution of Fig. 1.8, using

the method described in

Sect. 1.2.3. On 1 cm of Ar

in normal conditions there

are, on the average, m = 35

clusters (

= 1000); the eight

distributions then correspond

to track lengths of 0.14,

0.29, 0.57, 1.4, 2.9, 5.7, 14,

and 29 cm

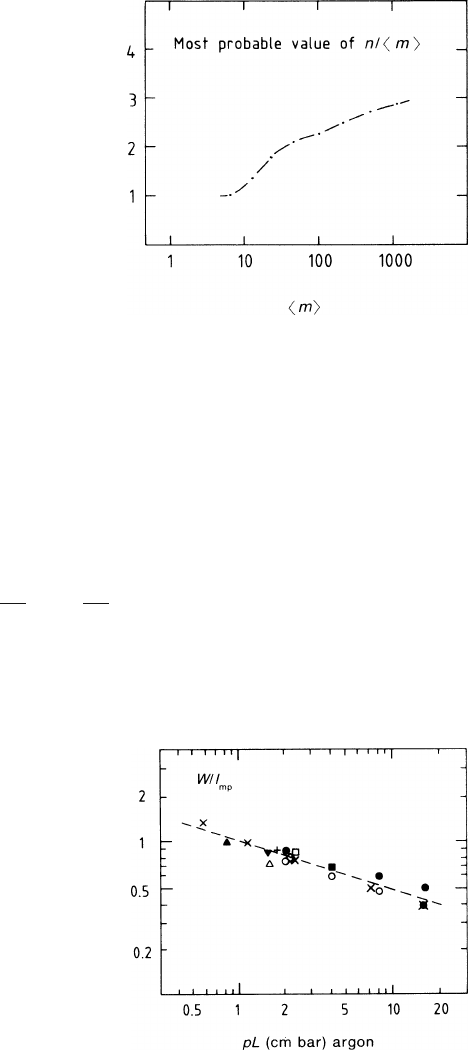
20 1 Gas Ionization by Charged Particles and by Laser Rays

Fig. 1.11 Values of the most

probable number of electrons

(expressed in units of m)

as a function of the mean

number m of clusters in

Ar, obtained from the data of

Fig. 1.8

shows this increase. It does not obey a simple law because it is inﬂuenced by the

atomic structure of argon. Neglecting the atomic structure, it approaches a straight

line; compare the remarks made on

after (1.49). The distributions of Fig. 1.10

also become more peaked, so that the ratio W/I

decreases from ∼1.3to∼0.3in

this range of m.

Relative widthsW/I

of measured pulse-height distributions quoted by Walenta

[WAL 81] are shown in Fig. 1.11 as a function of the gas sample thickness pL.The

ratio decreases with increasing pL. If we parametrize the decrease in the form of a

power law,









=[(pL)

: (pL)

]

, (1.37)

then from Fig. 1.12 we get k between −0.2 and −0.4. Since the ionization distri-

bution depends only on the cluster-size distribution and the number of clusters, it

depends on the sample length L and the gas pressure p through the product pL.

Fig. 1.12 Measured rela-

tive widths of pulse-height

distributions as collected by

Walenta [WAL 81]. The plot

shows ten different experi-

ments with the gas sample

thickness pL varying between

0.6 and 15 cm bar. The line is

drawn to guide the eye

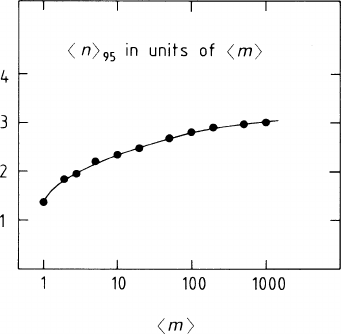
1.2 Calculation of Energy Loss 21

Fig. 1.13 Average ionization

after cutting the upper 5% of

the probability distribution,

calculated as a function of

the average number m of

clusters

For practical purposes, we introduce an upper cut-off E

in the transferred

energy at the level of 95% of the integrated probability distribution F(E):



F(E)dE = 0.95.

This allows us to compute the average ionization I

from the distributions of

Fig. 1.10. It is plotted in Fig. 1.13 as a function of m.

The role of the rare cases of large cluster sizes can be appreciated by looking

at Fig. 1.8. Since 1% of the clusters are larger than 30 electrons, it takes of the or-

der of 100 primary interactions (3 cm of argon NTP,

= 1000) to have one such

cluster among them. It will contribute about 10% to the total ionization. The larger

the number m of clusters one needs to sum, the smaller will be the probabilities

Q(n) that have to be taken into account. Let us compute the probability P that the

very rare event of a large cluster above n

occurs at least once in a number of m

clusters:

P = 1−[1 −Q(n

)]

≈ 1−e

−mQ(n

)

. (1.38)

It can be shown that (1.38) is correct within 10% as long as Q(n

) < 1/

√

(5m).

If the cluster-size distribution is not known, we ﬁrst calculate the energy loss

a given track length x and its probability distribution F(x,

). This is then converted

into the ionization distribution by dividing

by the appropriate value of W.The

energy transfer spectrum is independent of any other collision, and we have to sum

the contributions from as many collisions m = x/λ as there are on the length x,

using expression (1.31).

These days this is best achieved by the Monte Carlo method using a computer.

Working with analytical methods, one may also perform a stepwise convolution.

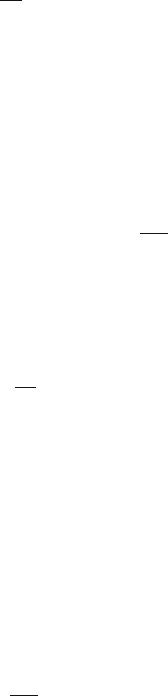
22 1 Gas Ionization by Charged Particles and by Laser Rays

For example,

F(2λ,

∞



−E)F(E)dE,

F(4λ,

∞



F(2λ,

−E)F(2λ, E) dE, etc. (1.39)

The review of Bichsel and Saxon [BIC 75] contains more details about how to build

up F(x,

Another way of constructing F(x,

) from F(E) was invented by Landau in 1944

[LAN 44]. He expressed the change of F(x,

) along a length dx by the difference

in the number of particles which, because of ionization losses along dx, acquire a

given energy E and the number of particles which leave the given energy interval

near

∂

F(x,

∞



F(E)[F(x,

−E) −F(x,

)] dE. (1.40)

(For the upper limit of integration, one may write ∞ because F(x,

)=0for

< 0.)

The solution of (1.40) is found with the help of the Laplace transform

F(x, p), which

is related to the energy loss distribution by

F(x, p)=

∞



F(x,

−p

, (1.41)

F(x,

+i∞+



−i∞+

F(x, p) dp. (1.42)

Here the integration is to the right (

> 0) of the imaginary axis of p. Multiplying

both sides of (1.40) by a e

−p

and integrating over

, we get

∂

F(x, p)=−

F(x, p)

∞



F(E)(1 −e

−pE

) dE, (1.43)

which integrates to

F(x, p)=exp

⎡

⎣

−x

∞



F(E)(1 −e

−pE

) dE

⎤

⎦

, (1.44)

because the boundary condition is F(0,

(

) or F(0, p)=1. Inserting (1.41)

into (1.44), Landau obtained the general expression for the energy loss distribution,

valid for any F(E):

F(x,

+i∞+



−i∞+

exp

⎡

⎣

−x

∞



F(E)(1 −e

−pE

) dE

⎤

⎦

dp. (1.45)

1.2 Calculation of Energy Loss 23

This relation was evaluated by Landau for a simpliﬁed form of F(E) that is ap-

plicable at energies far above the atomic binding energies where the scattering

cross-section is determined by Rutherford scattering and where the atomic struc-

ture can be ignored (see (1.32)). Inserting

F(E)=

N (1.46)

into (1.45), Landau was able to show that the probability distribution was given by

a universal function

(λ):

F(x,

) d



−





−



. (1.47)

Here

is the most probable energy loss, and

is a scaling factor for the energy

loss, proportional to x:

= x2

N. (1.48)

The function

(λ) and its integral

(λ) are given as a graph in Fig. 1.14. Computer

programs exist for the calculation of

and for the random generation of Landau-

distributed numbers: see K

olbig and Schorr [K

OL 84]. The integral probability for

an energy loss exceeding

∞



F(x,



) d





−



. (1.49)

We notice that 10% of the cases lie above the value of

that is three times the

FWHM above the most probable value. For large positive values of the argument,

(λ) tends to 1/λ

(λ) tends to 1/λ. The assumption (1.47) makes the Landau

Fig. 1.14 Landau’s function

(λ) and its integral

(λ).

The scale on the left refers to

, the one on the right to

24 1 Gas Ionization by Charged Particles and by Laser Rays

curve a valid description of the energy loss ﬂuctuations only in a regime of large

(corresponding to x ≈ 170cm in normal argon gas, according to an analysis of

[CHE 76] [see also Fig. 1.21]). We skip a discussion of Landau’s expression for

and of the normalization of his F(E). Let us remark, however, that, as a function of

the length x,

is proportional to xlogx. In practice, the Landau curve is often

used to parametrize energy loss distributions with a two-parameter ﬁt of

and

without reference to the theoretical expressions for them.

Generalizations of the Landau theory have been given by Blunck and Leisegang

[BLU 50], Vavilov [VAV 57], and others. The interested reader is referred to the

monograph by Bugadov, Merson, Sitar and Chechin [BUG 88] for a comparison of

these theories of energy loss.

When the summation of the energy lost over the length x has been achieved with

any of the methods mentioned above, the energy loss distribution must be converted

into an ionization distribution. We have to make the assumption that to every energy

loss

there corresponds, on the average, a number n of ion pairs according to the

relation

= nW, (1.50)

where W is the average energy for producing an ion pair (Sect. 1.1.3). Expression

(1.50) is to hold independently of the size or the composition of

(whether there

are one large or many small transfers), and W is to be the constant measured with

fully stopped electrons. It is hard to ascertain the error that we introduce with this

assumption. The W measured with fully stopped electrons is known to increase for

energy transfers below ∼ 1keV (Fig. 1.2).

Using (1.50), we obtain the probability distribution G(x, n) of the number n of

ionization electrons produced on the track length x:

G(x,n)=F(x,nW )W. (1.51)

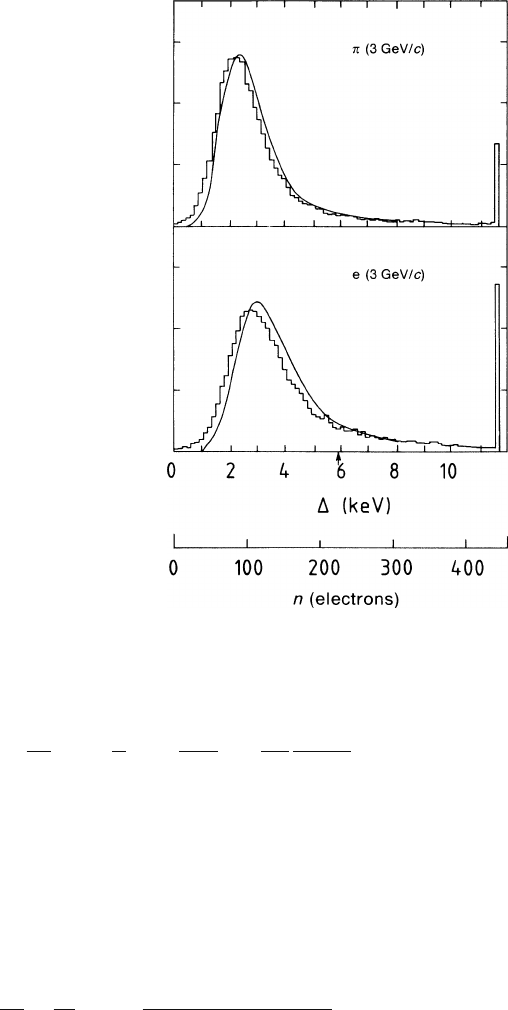
In Fig. 1.15 we show two examples of ionization distributions calculated in this

way by Allison and Cobb [ALL 80], compared with measured pulse heights from

Harris et al. [HAR 73] on argon samples of 1.5 cm thickness. Although there is a

small systematic shift and an excess of data at small n it is a remarkable fact that the

pulse-height distribution can be predicted so well using the theory described above.

For a comparison with the predictions of other models for calculating F(x,

),see

Allison and Cobb [ALL 80], and Ermilova, Kotenko and Merzon [ERM 77].

1.2.6 Velocity Dependence of the Energy Loss

Let us go back to (1.29). The term proportional to

is connected with Cerenkov

radiation of frequency

. It makes only a small contribution to the cross-section but

has a very characteristic velocity dependence. As soon as

vanishes, this radiation

will be emitted into the medium above a threshold given by

, (1.52)

1.2 Calculation of Energy Loss 25

Fig. 1.15 Measured pulse-

height distributions from

[HAR 73], compared with

the predictions of the

photo-absorption model of

[ALL 80]. The experimen-

tal overﬂow is collected in

the last bin. The horizontal

scale is normalized to the

peak of the

Fe spectrum

(5.9keV= 223 electrons)

where

jumps approximately from 0 to

increases. The emitted intensity in

photons per unit path length per unit of photon energy interval is then







1−



−

−1

. (1.53)

The behaviour of this intensity as a function of

= 1/(1 −

)

1/2

is plotted in

Fig. 1.16. The threshold can be expressed by

−1). (1.54)

We now discuss the velocity dependence of the remaining terms in (1.29). They

give the main contribution to the cross-section. The equation may be written in

the form



b + ln

[(1−

)

]

1/2



, (1.55)

where a and b depend on E and

(E) but are independent of