Білинський, Й.Й. Методи обробки зображень в комп’ютеризованих оптико-електронних системах: монографія

Подождите немного. Документ загружается.

тньо мати дві примежові криві, які отримані в результаті низькочас-

тотної фільтрації з різним параметром згладження

. При цьому спі-

льна точка даних примежових кривих і є крайовою.

2.2. Узагальнена математична модель перепаду інтенсивності

при дискретному його поданні

При введенні інформації про зображення в обчислювальний

пристрій приймальна система переводить оптичний розподіл інтенси-

вності зображення в цифрову форму. Таким чином, зображення дис-

кретизується відповідно до просторової періодичної ґратки матрич-

ного фотоприймача.

Тоді вихідний сигнал буде зображений у вигляді [1, 84, 131]:

(, ) (, ) (, )Hnm Hxy S xy

⋅

де

(,) ( ) ( )

fx y fy x y

Sxy x n y m

δδ

+∞ +∞

=−∞ =−∞

= −Δ ⋅ +Δ ⋅ −Δ ⋅ +Δ Δ Δ

∑∑

, а

і – пе-

ріоди ґратки матричного фотоприймача за відповідними осями;

– випадкові фазові вибірки.

Функція називається функцією дискретизації або функ-

цією вибірки.

(,)Sxy

У такому випадку вищенаведені перетворення згладження

примежової кривої можна виконати із застосуванням дискретної згор-

тки, яка має вигляд [51, 60]:

121

(,)

*( , ) ( , ) ( , )

kk D

Hnm HnkmkGkk

∈

=−−⋅

∑

, (2.9)

де

− деяка кінцева область у просторі аргументів, яка визначає вік-

но ;

(, )kk D∈

− коефіцієнт нормалізації фільтра, який забезпечує

незміщення середньої інтенсивності оброблюваного зображення від-

носно вхідного; − імпульсна характеристика згладженого

КІХ-фільтра, яка не повинна змінювати середнє значення зображення,

тобто виконувати умову

(, )Gk k

(,)

(, )1

kk D

Gk k

∈

∑

Коефіцієнти фільтра залежать від значень функції інте-

нсивності зображення примежової кривої в ковзному вікні D.

(, )Gk k

Дискретна згортка має свої особливості, оскільки виконання

повторного згортання з фільтром, що має іншу розмірність вікна при-

зводить до зміщення положення перетину примежових кривих фільт-

рованих зображень відносно точки асиметрії, що не спостерігається

при виконанні неперервної згортки. Це означає, що для отримання

шуканої точки, яка відповідає максимуму першої похідної, тобто точ-

ки асиметрії, необхідно виконати згортку тільки з фільтром, що має

певні вагові коефіцієнти, а також певну розмірність вікна.

Для дискретного подання примежової кривої з урахуванням

просторової неінваріантності передавальної функції матричного

приймача модель (2.5) трансформується для одновимірного простору

у вираз

1(()0,5

() exp

πσ

∗

)

⎡

⎤

−− −

=−

⎢

⎥

⎣

⎦

∑

, (2.10)

де

− зміщення центра примежової кривої від середини піксела по

осі n, що відповідає краю об’єкта вимірювання;

[,]nn

−

− кінцева об-

ласть аргументів в просторі примежової кривої по осі n, в околі яких

знаходиться крайова точка;

(nk)

−

− піксели примежової кривої, що

аналізуються, при цьому .

21n≥+K

Оскільки ширина міжпікселного простору може бути будь-

якою, а також будь-якою можуть бути й величина перепаду, то (2.10)

є формулою, що описує нормовану примежову криву з одиничним

перепадом інтенсивності.

Для двовимірного випадку примежова крива буде описана за

допомогою виразу [132]:

1(()0,5)(()0,5

(, ) exp

nk ml

Hnm

δγ

πσ σ

∗

⎡⎤

−− − + −− −

=−

⎢⎥

⎣⎦

∑∑

)

, (2.11)

де

− зміщення примежової кривої від середини піксела по осі m,

що відповідає краю об’єкта вимірювання;

()ml

−

− піксели примежової

кривої, що аналізуються, при цьому ;

21Lm≥+

[,]mm

−

− кінцева об-

ласть аргументів в просторі примежової кривої по осі m, в околі яких

знаходиться крайова точка.

Дискретні примежові криві, краї яких знаходяться в міжпіксе-

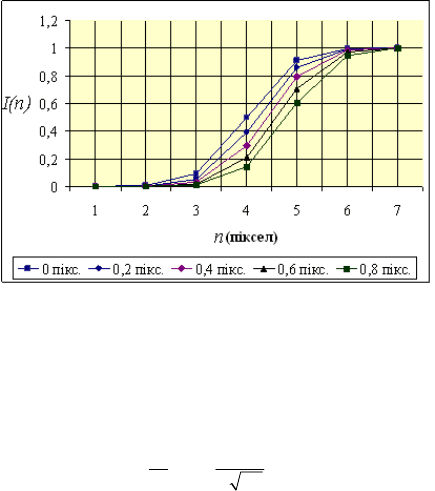
лному просторі, отримані за допомогою (2.10), наведені на рис. 2.3.

З графіка випливає, що будь-який край об’єкта вимірювання

подається примежовою кривою, яка буде асиметричною тільки в тому

випадку, коли край знаходиться на середині елементарного фотоп-

риймача ґратки, тобто піксела або по середині міжпікселного просто-

ру. Таким чином, при

примежова крива є асиметричною віднос-

но середньої точки, що відповідає краю об’єкта. Якщо ж центр при-

межової кривої знаходиться в міжпікселному просторі, то примежова

крива стає квазіасиметричною. При цьому параметр

змінюється в

деякому діапазоні, оскільки змінюється нахил функції примежової

кривої, тобто максимальне значення її похідної.

Рис. 2.3. Вигляд примежових кривих для декількох її положень

в міжпікселному просторі

Максимальне значення похідної неперервної примежової кри-

вої визначається як [56]:

max

σ π

∂

⎛⎞

⎜⎟

∂

⎝⎠

, (2.12)

Тоді функція розсіювання згідно з (2.3) та з урахуванням (2.12)

запишеться як

max

() exp

⎛

=−

⎜

⎝⎠

⎞

⎟

, (2.13)

де

Δ – найбільша зміна інтенсивності.

Формула (2.13) дозволяє розрахувати функцію розсіювання для

будь-якої примежової кривої, а сама примежова крива згідно з (2.7)

визначається [133]:

()

max max max

** exp

ItI xI

Hx dterf

xx x

−∞

⎛⎞

ΔΔΔ

=−=

⎜

⎜⎟

⎜

ΔΔ Δ

⎝⎠

∫

⎟

. (2.14)

У випадку дискретного подання зображення примежова крива

буде визначатися тільки у дискретних вузлах, що відповідають

центрам пікселів. Таким чином, при переході до дискретних парамет-

рів, коли крок дискретизації є

величиною постійною і однаковий по

осях, зображення задається в двовимірній ґратці з параметрами

, :

(, ) (,)

nym

fn m fxy

Δ=Δ

ΔΔ=

Тоді ступінь розмитості

необхідно подати з урахуванням

перепаду інтенсивності та ширини міжпікселного простору у вигляді

нормованої функції:

max min

(

)I I

−

, (2.15)

де

max

– максимальне значення інтенсивності примежової кривої;

min

– мінімальне значення інтенсивності;

− коефіцієнт пропорційності;

− ширина міжпікселного простору.

При цьому коефіцієнт пропорційності

відповідає відношен-

ню нормованого його значення до кроку дискретизації

норм

Функція примежової кривої внаслідок дискретного подання

сигналу (2.10) з урахуванням (2.15) для одновимірного простору на-

буде виду:

222

max min max min

(( ) 0,5 )

**( ) exp

() ()

nk I

IId IId

πδ

ββ

⎛⎞

Δ−−

=−

⎜⎟

−−

⎝⎠

∑

−Δ

. (2.16)

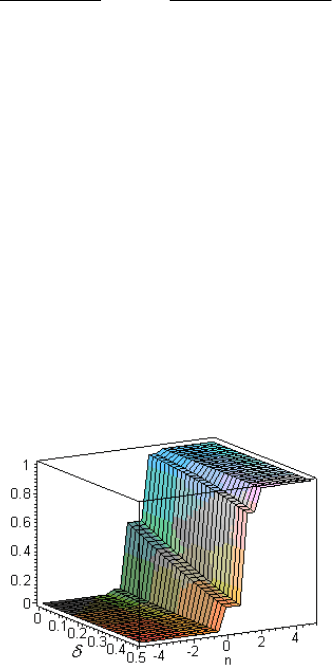
Поверхня, що характеризує примежову криву в міжпікселному

просторі, наведена на рис. 2.4. Зміщення примежової кривої в міжпік-

селному просторі

призводить до перерозподілу інтенсивності пік-

селів, що відносяться до цієї кривої.

Максимальне значення перепаду інтенсивності, тобто макси-

мум першої похідної при зміщенні примежової кривої в міжпікселно-

му просторі змінюється. Це означає, що для одного й того ж краю

об’єкта, отриманого матричним фотоприймачем, примежова крива

залежно від його положення має різний ступінь розмитості

, який

змінюється в деякому діапазоні. Тому модель дискретної примежової

кривої повинна бути універсальною та використовувати приведене

значення ступеня розмитості, яке б задовольняло примежову криву

при будь-яких її положеннях в міжпікселному просторі.

Рис. 2.4. Поверхня, що характеризує вигляд примежової кривої та

положення крайової точки в міжпікселному просторі

Примежова крива, на якій знаходиться крайова точка об’єкта

вимірювання, визначається параметрами максимуму та мінімуму ін-

тенсивності примежової кривої, розмірами міжпікселного простору, а

також значенням першої похідної, що відповідає максимальному пе-

репаду інтенсивності.

2.3. Математична модель квазіасиметричного

перепаду інтенсивності

Якщо положення краю примежової кривої знаходиться в між-

пікселному просторі та його зміщення

не дорівнює 0 і 0,5 або у ви-

падку відхилення кривої від функції розподілу, що задається форму-

лою (2.16), то примежова крива стає квазіасиметричною. При цьому

крайова точка знаходиться в околі піксела з максимальним значенням

першої похідної.

Для субпікселного визначення краю, необхідно знайти єдиний

параметр – це приведений ступінь розмитості такої примежової кри-

вої

пр

. При цьому можна скористатися вищенаведеним математич-

ним апаратом, який був застосований для опису асиметричної приме-

жової кривої [85, 133].

Оскільки параметр згладження не є критичним і безпосередньо

пов’язаним з максимумом першої похідної, знайдемо нормоване

значення цієї похідної

мax

∂

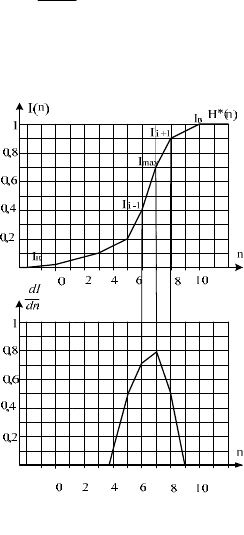
. Квазіасиметрична примежова крива, а

також значення максимуму першої похідної, що визначає номер пік-

села, в околі якого знаходиться край, наведена на рис. 2.5.

Рис. 2.5. До визначення квазіасиметричної примежової кривої

Запропонований підхід знаходження приведеного значення по-

хідної базується на використанні двох частин цієї кривої: нижньої, що

відповідає перепаду інтенсивності від нижнього рівня примежової

кривої до піксела з максимальним значенням похідної; верхньої, що

відповідає перепаду інтенсивності від піксела з максимальним зна-

ченням похідної до піксела з інтенсивністю верхнього рівня [134].

Похідні нижньої та верхньої частини кривої можна визначити

згідно з виразами:

max

;

(2)

(2 )

∂−

⎧

⎪

∂−+

⎪

⎨

∂−

⎪

∂−−

⎩

III

nI II

III

nIII

(2.17)

де

max

– інтенсивність піксела на примежовій кривій, що відповідає

максимуму першої похідної;

– інтенсивність нижнього та вер-

хнього рівня примежової кривої, відповідно;

– інтенсивність пік-

села, що вибирається з умови:

то II

+−

−

+−

∂∂

⎧

⎪

∂∂

⎨

∂∂

⎪

∂∂

⎩

де

−

∂

– значення похідних зліва та справа від максимуму

похідної, відповідно;

−

– інтенсивність пікселів зліва та справа

від піксела, що відповідає максимальному значенню похідної.

Приведене значення максимуму похідної на підставі розв’язку

(2.17 ) з урахуванням умови (2.12) визначається як

max

max max

()

2(2)(2

вн

мax нв

нв

IIII

III

nnnIIIIII)d

−−

∂∂∂

⎛⎞

=+=

⎜⎟

∂∂∂ −+−−

⎝⎠

. (2.18)

У такому випадку ступінь розмитості примежової кривої згідно

з (2.12) з урахуванням (2.18) визначається

max max

max

(2)(2 )

()2

нв

вн

IIII Id

IIII

−+ − −

−−

. (2.19)

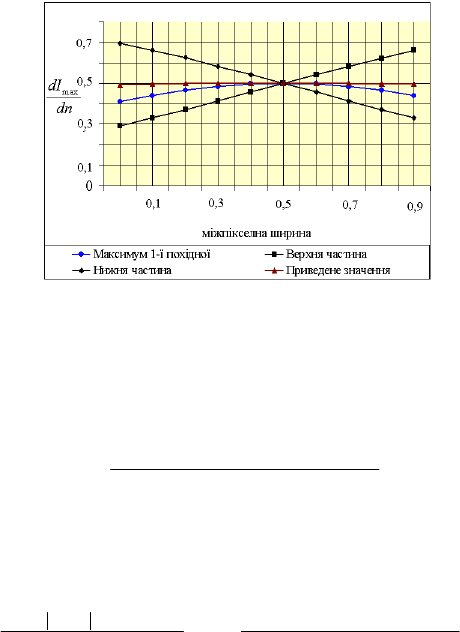
Залежності максимуму похідних примежової кривої для будь-

яких положень краю в міжпікселному просторі, а також залежності

похідних нижньої та верхньої частини примежової кривої та приведе-

ної похідної наведені на рис. 2.6. З графіку видно, що приведена мак-

симальна похідна постійна для будь-яких положень краю в міжпіксел-

ному просторі.

Рис. 2.6. Максимум похідних залежно від положення примежової

кривої в міжпікселному просторі

Використовуючи формулу (2.13) отримаємо функцію розсію-

вання для даної примежової кривої

222

max

max max

(I ) ( )

*( ) exp

(2 )(2 )

вн

нв

IIIn

III II Id

⎛⎞

−−

=−

⎜⎟

−+ − −

⎝⎠

. (2.20)

Дискретне подання такої примежової кривої (2.15) тоді опису-

ється виразом:

max

max max max max

()

(( ) 0,5 ) (I ) ( )

**( ) exp

(2 )(2 ) (2 )(2 )

вн

n в n в

IIII

nk I I I

III II Id III II Id

δπ

ββ

−−

⎛⎞

−− − − −

=−

⎜⎟

−+ − − −+ − −

⎝⎠

∑

. (2.21)

Поверхня, що характеризує положення крайової точки приме-

жової кривої в міжпікселному просторі, залежно від величини інтен-

сивності піксела, що відповідає максимальному перепаду

інтенсивно-

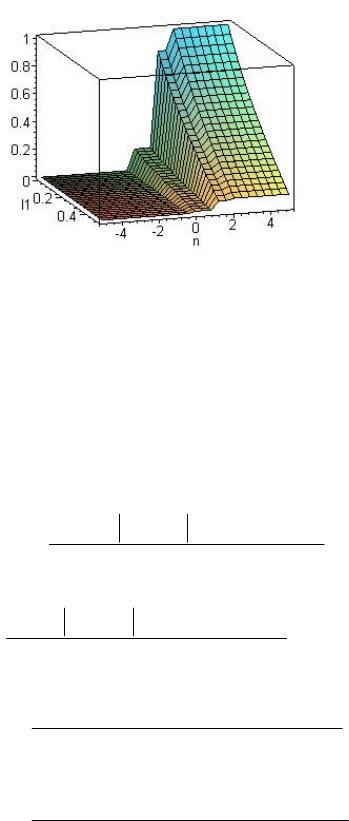
сті, тобто максимальному значенню першої похідної, наведена на

рис.

2.7 [135–138].

Рис. 2.7. Поверхня, що характеризує положення примежової кривої

залежно від величини інтенсивності піксела, що відповідає

максимуму першої похідної

У результаті зростання перепаду інтенсивності величина мак-

симального значення похідної зростає. При цьому, змінюється й кут

нахилу примежової кривої, а отже, параметр ступеня розмитості

Модель дискретної примежової кривої інтенсивності для двовимі-

рного випадку набуде виду:

max

max max

max

max max

2max 2 2

max 2 max 2 2 2

()

**( , )

(2 )(2 )

()

(2 )(2 )

(( ) 0,5 ) (I ) ( )

exp

(2 )(2 )

вн

nnnn

нв

nnn nn n

вн

mmmmпр

нв

mmm mm m

вн

nn n nn

нв

nnn nn n

IIII

Hnm

III II Id

IIII

III IIId

nk I I I

III II Id

πδ

−−

=×

−+ − −

−−Δ

××

−+ − −

⎛⎞

−− − − −

×−

⎜

−+ − −

⎝

∑

2max 2 2

max 2 max 2 2 2

(( ) 0,5 ) (I ) ( )

exp ,

(2 )(2 )

вн

mm mmm

нв

mmm mm m

ml I I I

III IIId

πδ

⎟

⎠

⎛⎞

−− − − −

×−

⎜⎟

−+ − −

⎝⎠

∑

(2.22)

де

max

– інтенсивність пікселів, що відповідають максимально-

му значенню похідної по осі і , відповідно; і

нв

інтен-

сивність пікселів, які вибираються аналогічно умові (2.17);

–

зміщення краю примежової кривої відносно центра піксела по осі

, відповідно.

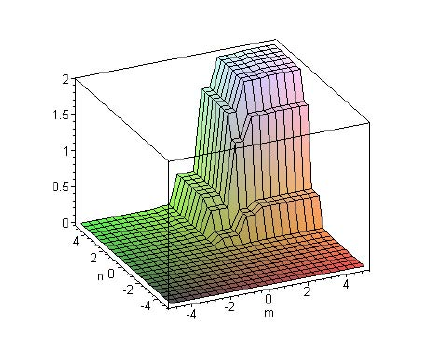
Поверхня, що характеризує двовимірну дискретну примежову

криву краю об’єкта в координатах n, m, наведена на рис. 2.8.

Рис. 2.8. Поверхня, що характеризує двовимірну примежову криву

Двовимірна примежова крива має різний нахил по відповідних

осях, оскільки величини максимальних перепадів інтенсивності, що

відповідають максимумам перших похідних, мають різні значення. В

реальних випадках границя між фоном та зображенням об’єкта може

мати будь-яку орієнтацію. Це вимагає знаходження зміщення краю

відносно центра піксела по осі і відповідно.

Таким чином, для отримання функції квазіасиметричної при-

межової кривої необхідно визначити параметри примежової кривої,

тобто її величину перепаду, а також максимальні значення похідних

по відповідних осях.