Білинський, Й.Й. Методи обробки зображень в комп’ютеризованих оптико-електронних системах: монографія

Подождите немного. Документ загружается.

Методи визначення максимуму інтенсивності світлової плями

основані на аналізі інтенсивності пікселів, які знаходяться в околі пік-

села з максимальною інтенсивністю.

До таких методів відноситься метод Гаусса, який використо-

вує яскравість трьох суміжних пікселів в околі досліджуваного мак-

симуму плями або лінії і припускає, що форма досліджуваного макси-

муму відповідає профілю (перетину) Гауcса. Це припущення є приб-

лизно правильним [113].

Справжній розподіл, звісно, не є Гауссовим, тому що кожен пі-

ксел об’єднує (інтегрує) світло, що потрапляє на нього. У зв’язку з

чим цей метод є наближеним і працює тільки з плямами, що наближе-

ні за формою розподілу інтенсивності до Гауссової. Оскільки функція

містить цілі числа в діапазоні 0– 255 і обчислення логарифма може

бути виконано пошуком в таблиці, але все ж таки метод у порівнянні

з іншими має більший час обробки.

Алгоритм центра мас також допускає розподіл інтенсивності

вздовж одного рядка фотоматриці та вважається, що відповідає Гаус-

совому розподілу. Положення максимуму обчислюється середньоз-

важеним методом і при цьому може використовувати не тільки 3,

але й 5 або 7 точок. Цей метод працює швидше, ніж метод Гаусса, але

точність методу нижча [114].

Лінійна інтерполяція допускає простий лінійний взаємозв’язок

розподілу інтенсивності пікселів перед і після піку [115]. Однак даний

алгоритм не оптимальний, оскільки є дуже чутливим до шуму, а при

великій різниці інтенсивності пікселів, що досліджуються на предмет

піку, похибка методу зростає. Однак для швидкоплинних процесів за-

лишається ефективним, оскільки має мінімальний час обробки.

Неперервний варіант знаходження максимуму визначається з

розвиненням в ряд Тейлора сигналу інтенсивності в околі максимуму

та називається методом параболічної оцінки. Якщо максимум розпо-

ділу знаходиться в координаті f(x+δ), а величина сигналу f(x) і сигна-

лів f(x-1), f(x+1) відома, тоді можна оцінити дискретну похідну, яка

дозволяє розрахувати зміщення піку відносно центра піксела з коор-

динатою f(x).

Даний метод є ефективний для дифракційно-обмежених плям. У

випадку плями з великим значенням ступеня розмитості

, коли вер-

шина піку стає не вираженою, знаходження максимуму ускладнюється.

Детектор Blais i Roux являє собою фільтри четвертого та вось-

мого порядку [115]. Результати показують, що оператор четвертого

порядку має кращі характеристики ніж оператор восьмого порядку у

випадку ширини максимуму піку, що відповідає одному пікселу. А у

випадку ширини максимуму піку більшого за 2 піксела, оператор во-

сьмого порядку має кращі характеристики.

Детектори Штегера можуть бути використані як для вимірю-

вання світлової плями, так і для вимірювання світлової лінії [116].

Принцип алгоритму Штегера 2D такий же, як і в 1D випадку,

тільки функція інтенсивності тепер залежить від двох змінних. Споча-

тку обчислюються похідні rx, ry, rxx, ryy, rxy, потім знаходять харак-

терний напрям, перпендикулярний до шуканої лінії, n=(nx, ny), як но-

рмований вектор відповідний максимальному значенню.

В цілому, розглянуті алгоритми вимагають великих затрат ча-

су при використанні середніх за розміром матриць.

За швидкістю роботи перевагу можна віддати алгоритму пара-

болічної оцінки, а за точністю – методу центра мас або методу Гаусса.

Для підвищення точності можуть бути поєднані вищенаведені алго-

ритми, але при цьому різко зростає час обробки, що не завжди є доці-

льним [51, 60].

РОЗДІЛ 2

ТЕОРЕТИЧНІ ЗАСАДИ СУБПІКСЕЛНОЇ ОБРОБКИ

ДИСКРЕТНОЇ ВИМІРЮВАЛЬНОЇ ІНФОРМАЦІЇ

У результаті проведеного в першому розділі аналізу відомих

методів субпікселного визначення та виділення простих елементів

об’єкта на зображенні встановлено: по-перше, дані задачі відносяться

до класу некоректних; по-друге, існуючі методи працюють, як пра-

вило, при низькому рівні шумів; по-третє, в результаті попередньої

обробки деяка інформація про край об’єкта неминуче втрачається.

Введення зображення в цифровий канал обробки супроводжу-

ється його дискретизацією. Просторовий спектр дискретизованого зо-

браження складається з періодичної просторової ґратки спектрів вхід-

ного зображення, зміщених один відносно одного на частоти, кратні

частоті

−

(2 )d

кроку дискретизації . Якщо спектр вхідного зобра-

ження необмежений або має частоти, що перевищують частоту Найк-

віста

−

, то дискретизоване зображення згідно з теоремою ві-

дліків, відтворити без спотворення, а отже, отримати його координати

краю з високою точністю неможливо [108, 109].

Детектори країв побудовані таким чином, що дають великий

вихід інтенсивності при різких змінах перепаду, а одна з причин ви-

никнення різких змін – це додавання до інтенсивності піксела різних

значень шуму. Шуми в різних пікселах, як правило, не корелюють,

тобто можуть дуже сильно відрізнятися один від одного. Таким чи-

ном, основна проблема задачі визначення країв – це шуми зображення

[110].

За визначенням Адамара [6] математична задача коректна, коли:

– для кожної функції заданого класу функцій існує розв’язок

визначеного класу (умова існування);

– розв’язок є єдиним у цьому класі;

– залежність розв’язку від цієї функції є неперервною (непере-

рвність). Вимога неперервності пов’язана з вимогою стійкості або ро-

бастності рішення. Тому і друга частина розв’язування задачі визна-

чення та виділення краю, якою є чисельне диференціювання, є неко-

ректною, оскільки не має неперервної залежності розв’язку від вхід-

них даних.

Найбільш ефективним підходом до розв’язування некоректних

задач є метод регуляризації Тихонова, основна ідея якого полягає у

введенні неперервних наближень неперервного оператора, а відомим

прикладом такого розв’язку є задача згладжування функції на кінце-

вій множині точок, які піддані впливу деякої помилки [111–116]. То-

му, найбільш природним використанням регуляризації є апроксима-

ція та інтерполяція даних аналітичної функції. Фізичним обґрунту-

ванням цього є гладке зображення (без шуму) в силу властивостей

процесу обробки зображення: зображення відповідає функції з обме-

женим спектром.

Регуляризоване рішення має просту форму, якщо результатом

рішення є оператор згортки. Таким чином, якщо дані задані на регуля-

рній сітці та задовольняють відповідні граничні умови, то рішення мі-

німізації функції апроксимації може бути отримано, використовуючи

згортку з відповідним фільтром, який, як правило, є фільтром низьких

частот.

На сьогодні для виділення, а також для визначення краю вико-

ристовують три основних типи фільтрів: смугові, з обмеженим носієм,

з мінімальною невизначеністю. До третього типу можна віднести фі-

льтри за допомогою функції Гаусса, яка мінімізує добуток величини

просторового розкиду та частотного інтервалу й дозволяє перетвори-

ти неперервну обмежену функцію в цілу [117–120].

На підставі вищенаведеного в роботі запропонований метод

субпікселної локалізації краю об’єкта та виділення його контуру на

основі знаходження спільних точок примежових кривих зображень

об’єкта вимірювання, отриманих у результаті гауссової низькочастот-

ної фільтрації з різним ступенем згладження. При цьому співвідно-

шення сигнал/шум не повинно перевищувати 6 dB при ступені розми-

тості в діапазоні до 2,6.

Запропонований метод дозволить отримати координати краю

зображення об’єкта вимірювання з субпікселною точністю та знизити

похибку вимірювання КОЕС в цілому. Для реалізації цього методу

необхідно отримати математичні моделі дискретних примежових кри-

вих, моделі локалізації крайової точки та провести їхні дослідження.

2.1. Узагальнена математична модель перепаду

інтенсивності на основі властивостей оптичної системи

та фотоприймача

У геометричній оптиці передбачається, що в однорідному се-

редовищі світлові промені завжди поширюються прямолінійно. При

такому припущенні промені, що попадають в площину матричного

фотоприймача після проходження через оптичну систему, формують

геометричну проекцію [50, 56]. У багатьох випадках випромінювання,

що формує зображення, може вважатися квазімонохроматичним у то-

му розумінні, що ширина його спектра мала в порівнянні з централь-

ною частотою випромінювання і залежність між інтенсивністю зобра-

ження й об'єкта може бути виражена інтегралом суперпозиції виду [1,

7, 51, 84, 87]

00 00

(, ) (, ; , )

ii j i j

I x y G x y x y dx dy

∞∞

−∞ −∞

∫∫

де – імпульсна реакція системи, тобто розподілу інтен-

сивності в площині зображення,

що утворює точкове джерело світла.

(, ; , )

Gx y x y

Імпульсний відгук часто виявляється просторово-інваріантним

і тоді залежність «вхід-вихід» виражається інтегралом згортки

000000

(, ) ( , )(, )

ii j i j 0

xy Gx xy yIxydxdy

∞∞

−∞ −∞

=−−

∫∫

. (2.1)

У теорії регулювання й теорії зв'язку існує декілька методів

опису передатних характеристик лінійних ланок і систем, основаних

на реакції ланки або системи на вплив спеціального вигляду сигналу.

Найпоширенішими передатними характеристиками є: функція розсі-

ювання точки (ФРТ) та функція розсіювання лінії (ФРЛ), а також пе-

рехідна функція системи (примежова крива) і комплексна оптична пе-

редавальна функція (ОПФ) [15, 56, 121–124].

ФРТ або імпульсна функція характеризує реакцію оптичної си-

стеми на імпульс випромінювання, тобто на просторову

-функцію

або на точкове джерело. При розгляді одновимірної картини розподілу

інтенсивності можна замість ФРТ використовувати ФРЛ. Така функ-

ція описує розподіл освітленості зображення лінії, створюваної опти-

чною системою.

Якщо сигнали подані у вигляді просторово-частотних спектрів,

то передатні властивості двовимірних ланок характеризуються їх

ОПФ, які визначаються як відношення комплексного амплітудного

спектра сигналу на виході ланки до комплексного амплітудного спек-

тра сигналу на його вході. Залежність коефіцієнта передачі модуляції

від просторової частоти описується функцією передачі модуляції

(ФПМ) [117].

Ще однією важливою характеристикою оптичної системи є

функція передачі фази ФПФ [121]. ФПФ характеризує здатність дво-

вимірної передавальної ланки зберігати координати окремих точок на

зображенні щодо координат цих точок на об'єкті.

Таким чином, ФПМ і ФПФ повністю визначають оптичну пе-

редатну функцію, тобто передатні властивості будь-якої оптичної

ланки, а цей апарат частотно-передатних функцій у відношенні до

об'єктива може бути застосований тільки для ізопланатичних облас-

тей, у межах яких передатні властивості об'єктива практично залиша-

ються незмінними, але як правило, мають досить складну форму.

Вважатимемо, що оптико-електронні канали КОЕС, призначені

для вимірювання геометричних параметрів об’єктів, мають велику кі-

лькість оптичних передатних ланок, тому ОПФ оптичного тракту бу-

демо апроксимувати функцією Гаусса [56, 117, 125]. Оскільки у такої

ОПФ відсутня фазова складова, тобто ФПФ дорівнює нулю, то амплі-

тудна складова ОПФ або ФПМ може бути описана такою ж функцією

Гаусса, що і ОПФ [56, 122].

Передатні характеристики таких елементів, як ПЗЗ-матриць,

досліджені у працях [44, 123–126] показують, що ПЗЗ-матриця не є

просторово інваріантною оптичною передатною ланкою, оскільки

ФПФ матриці має періодичний характер і дорівнює нулю тільки в тих

точках, де краї зображення збігаються з краями фотоелементів.

Тому розглянемо розподіл сигналу інтенсивності у випадку

безперервного фотоприймача , який визначається [4, 15, 127–130]:

(,) (,) (,) (,)

xy kHxy Oxy Pxy

∗

= ⋅ ∗∗ ∗∗

, (2.2)

де

– апертурні функції оптичної системи та елемента

фотоприймального пристрою, відповідно

; – розподіл інтенси-

(,)Oxy (, )Pxy

(,)Hxy

вності об’єкта спостереження; – коефіцієнт перетворення світлое-

нергетичних величин в електричні.

Центральна гранична теорема стверджує, що закон розподілу

суми випадкових величин необмежено наближається до нормального

закону та має аналог в теорії лінійної фільтрації: добуток декількох

просторово-частотних характеристик окремих ланок оптичної системи

наближається до гауссової форми, коли їх кількість стає великою [56,

114]. Ця обставина надає особливе значення гауссоїді, яка дає змогу

досить точно описати просторово-частотні властивості реальних оп-

тико-електронних приладів.

Вважатимемо, що КОЕС, призначені для виділення геометрич-

них ознак і вимірювання геометричних параметрів об’єктів, мають ве-

лику кількість оптичних передатних ланок і ОПФ оптичного тракту

будемо апроксимувати функцією Гаусса.

Математичний запис нормованої гауссоїди обертання має ви-

гляд [7]:

(,)

exp

Gxy

⎛⎞⎛⎞

=− ⋅−

⎜⎟⎜⎟

⎝⎠⎝⎠

, (2.3)

де σ – середньоквадратичний розподіл перепаду інтенсивності відби-

того світла на межі (постійна закону Гаусса); х, y – координати межі.

Якщо

, то різкоконтрастний розподіл інтенсивності

перетворюється в розмите зображення. Ступінь розмитості тим біль-

ший, чим більша величина

(,)Hxy

Нехай об’єкт має двовимірний розподіл інтенсивності

різкого краю [130]:

(,)Hxy

(,)

при х x

Hxy

при x

для будь яких y

⎧

⎪

⎨

⎪

−

⎩

(2.4)

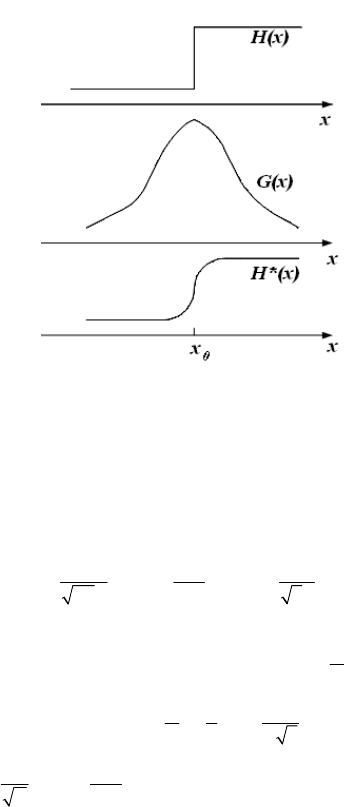
Функція розподілу сигналу різкого краю на неперервному фо-

топриймачі по осі x за рахунок функції однозначно пов’язана з

нею і визначається її виглядом, рис. 2.1.

(,)Gxy

Рис. 2.1. Вигляд примежової кривої до та після проходження через

лінійну оптичну систему з функцією розсіювання

()Gx

Враховуючи (2.3), нормовану межову криву цієї системи (оскі-

льки ОПФ і ФРЛ лінійної оптичної системи пов’язані між собою пря-

мим і зворотним перетворенням Фур’є)

запишемо у вигляді функції

[56, 121

–124]

() exp

Hx dterf

σσ

∗

−∞

⎡⎤

⎛

=−=

⎢⎥

⎜

⎝⎠

⎣⎦

∫

⎞

⎟

. (2.5)

Даний вираз відповідає функції Лапласа

⎛

⎝

⎜

⎞

⎠

⎟

, тобто

() 1

Hx erf

∗

⎡

⎤

⎛⎞

Φ= +

⎜⎟

⎢

⎥

⎜⎟

⎝⎠

⎣

⎦

, (2.6)

де

()

exp

erf z du

⎡⎤

=−

⎢

⎢⎥

⎣⎦

∫

⎥

– інтеграл імовірності [125].

Таким чином, маючи в полі фотоприймача край об’єкта, можна

визначити функцію розподілу цього сигналу в напрямку, перпендику-

лярному до межі краю, а отже визначити параметр

гауссоїди обер-

тання або, знаючи параметри ОПФ, а отже, й параметри ФПМ для

ізопланатичної системи параметр

гауссоїди обертання апріорно бу-

де відомим.

Формули (2.5) і (2.6) не враховують передатні характеристики мат-

риці відеосенсорів, оскільки ПЗЗ-матриця не є просторово інваріант-

ною оптичною передатною ланкою та має періодичний характер. За

рахунок просторової неінваріантності максимальна похибка вимірю-

вань координат деякої точки за допомогою ПЗЗ-матриці з урахуван-

ням розміру піксела, який дорівнює кроку дискретизації , досягає

половини кроку (без врахування масштабних перетворень), тобто

()

max

Проведемо аналіз впливу функції розсіювання на примежову

криву з використанням гауссової функції. Для цього достатньо прове-

сти одновимірний аналіз, результати якого можна легко інтерпретува-

ти у двовимірному просторі.

Гауссіан не є єдиним ядром згладжування, але, окрім приглу-

шення шуму, має ряд інших важливих особливостей. По-перше, ядра

гауссіана є відокремлювальними, тобто згортка з ядром фільтра еквіва-

лентна згортці з двома одновимірними ядрами – за напрямками х і у [7]:

()

22 2 2

22 2

111

, , exp exp exp

22 2 2

xy x y

Gxy

πσ σ σ σ

πσ πσ

⎛⎞⎛⎞

⎛ ⎞ ⎛⎞ ⎛

=−= −× −

⎜⎟⎜⎟

⎜ ⎟ ⎜⎟ ⎜

⎝ ⎠ ⎝⎠ ⎝⎠

⎝⎠⎝⎠

⎞

⎟

, (2.7)

де σ – параметр ступеня згладжування.

Це означає, що гауссіан можна факторизувати, отримавши до-

буток двох одновимірних гауссіанів.

По-друге, виконуючи згортку гауссіана з гауссіаном можна

отримати ще один гауссіан:

GG G

σσ

, (2.8)

тобто, можна отримати згладжене зображення, повторно згладивши

уже згладжене зображення.

І, по-третє, в результаті згладження примежові криві вхідного

та фільтрованого зображення мають єдину спільну точку в області

найбільшого значення похідної, яка є крайовою та згідно з формулою

(2.5) її координата знаходиться на рівні 0,5 сигналу інтенсивності.

Обґрунтуємо це твердження. При повторному згладженні зо-

браження гауссіаном, що має одне і те ж саме ядро, параметр ступеня

згладження на підставі формули (2.8) становить

σσ

і, якщо

згладження повторюється, то в загальному випадку визначається:

, де – порядковий номер згортки.

В результаті проведених досліджень встановлено, що спільні

точки примежових кривих, отриманих в результаті повторного згла-

дження зображення при

***HH

, також знаходяться на рівні 0,5

нормованих примежових кривих і мають у цій точці максимальне

значення похідної.

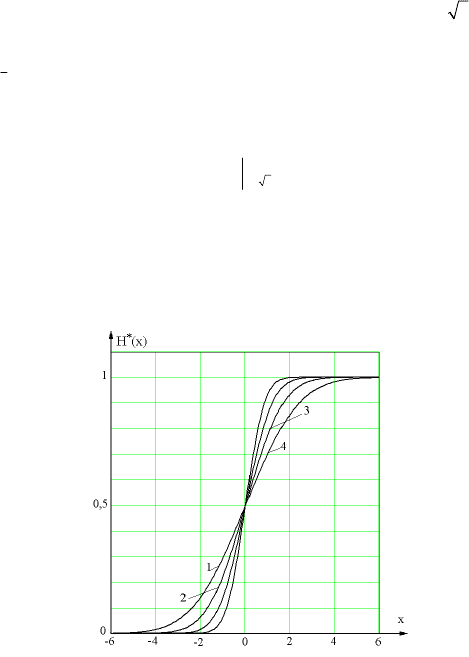
Нормовані примежові криві, які отримані в пакеті Mathcad для

декількох значень

згідно з формулою (2.5), наведені на рис. 2.2.

Рис. 2.2. До визначення точки перетину

нормованих межових кривих

З графіка видно, що точка перетину даних кривих знаходиться

на рівні 0,5 для будь-яких значень параметра згладжування

З вищенаведених пояснень випливає, що для знаходження кра-

йової точки об’єкта, яка описується примежовою кривою (2.5), доста-