Білинський, Й.Й. Методи обробки зображень в комп’ютеризованих оптико-електронних системах: монографія

Подождите немного. Документ загружается.

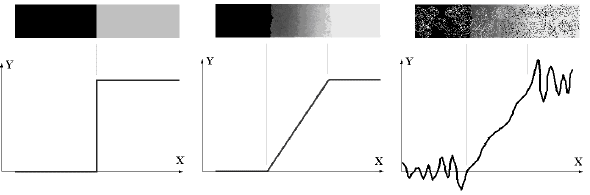
Вибір порога є одним із ключових питань виділення перепадів.

При занадто високому рівні порога не будуть виявлені структурні

елементи з низьким контрастом. Навпаки, занадто низький рівень по-

рога буде причиною того, що шум буде прийнятий за перепад. Для

позначення положення перепадів на зображенні часто формують кон-

турний препарат.

Інший важливий підхід до виявлення перепаду складається в

апроксимації фрагмента реального зображення деяким ідеальним од-

но- або двовимірним перепадом. Якщо апроксимація виявляється до-

сить точною, то вважається, що перепад існує, і йому приписуються

параметри ідеального перепаду.

а б в

Рис. 1.4. Моделі перепадів інтенсивності:

а – модель ідеального перепаду інтенсивності та його профіль;

б – модель похилого перепаду інтенсивності та його профіль;

в – модель зашумленого похилого перепаду інтенсивності та його

профіль

На практиці оптичні обмеження, дискретизація, а також недос-

коналість інших елементів системи реєстрації зображень призводять

до отримання розмитих перепадів інтенсивності. Причому ступінь ро-

зфокусування визначається такими чинниками, як якість системи ре-

єстрації, крок дискретизації і умови освітлення, при яких зображення

було отримане. В результаті перепади інтенсивності точніше моде-

люються похилим профілем, подібним, як на рис. 1.4б. Крутизна по-

хилої ділянки обернено пропорційна ступеню розфокусування краю.

У такій моделі вже немає тонкої траєкторії (шириною в один піксел).

Натомість точкою перепаду інтенсивності тепер є будь-яка точка, що

лежить на похилій ділянці профілю, а сам перепад є зв'язною множи-

ною, утвореною всіма такими точками. «Ширина» такого перепаду

визначається довжиною похилої ділянки, на якій здійснюється перехід

від початкової інтенсивності до кінцевої. Така залежність виглядає

цілком осмислено: розмиті перепади виглядають широкими, а різкі

перепади – тонкими.

На рис. 1.4в наведений зашумлений перепад. У цьому випадку

перепад інтенсивності моделюється кривою, яка має різну крутизну

похилої ділянки в кожній точці профілю похилої. Ширина такого пе-

репаду не може бути визначена точно у зв’язку з відсутністю точного

значення верхнього та нижнього рівнів перепаду.

Ознаки світлової плями та лінії

Світловою плямою називають відносно малу область зобра-

ження, яскравість якої значно відрізняється від її інтенсивності в око-

лі.

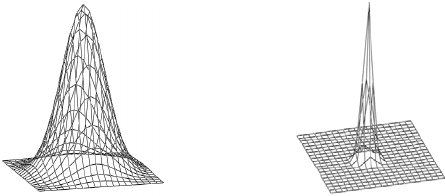
На рис. 1.5 наведені дві відомі моделі розподілу інтенсивності

світлової плями, розміри яких у площині матричного фотоприймача

складають від декількох пікселів до сотні пікселів, і які мають вид фу-

нкції Гаусса або дифракційно-обмеженої плями розсіювання [55].

а б

Рис. 1.5. Моделі розподілу інтенсивності світлової плями:

а – вигляд функції Гаусcа; б – вигляд дифракційно-обмеженої плями

Більша частина енергії (більше 80 %) світлової плями концент-

рується поблизу її енергетичного центра. На рис. 1.5а наведено зобра-

ження плями розсіювання, на рис. 1.5б – плями розсіювання при на-

кладенні адитивного шуму.

Особливістю реєстрації таких світлових плям матричним фо-

топриймачем, які наведені на рис. 1.6а,б, є невідповідність розподілу

яскравості з розподілом інтенсивності електричного сигналу фотоп-

риймачем. Ця неоднозначність виникає у зв’язку з наявністю шуму, а

також дискретним поданням зображення.

а б

Рис. 1.6. Пляма розсіювання:

а – без шуму; б – зашумлена

Таким чином, одна й та ж світлова пляма в результаті прохо-

дження через оптичний тракт і фотоприймальну систему може набу-

вати різного вигляду. Її максимум може мати пік з тупою вершиною

(рис. 1.7а); симетричною та несиметричною вершиною (рис. 1.7б, в).

а б в

Рис. 1.7. Типи піків світлових плям:

а – з тупою вершиною; б – симетричний; в – несиметричний

Ще одним важливим простим елементом сцени для КОЕС є

світлова лінія, яка визначається також розподілом інтенсивності. Світ-

лова лінія повинна мати U-подібну (або П-подібну) форму в напрямку,

перпендикулярному до напрямку лінії. Кожна лінія може бути розгля-

нута як сукупність світлових плям, центр якої в поперечному перерізі

відповідає положенню максимуму інтенсивності, тобто положенню

піку аналогічно світловій плямі [56, 59].

У випадку лінійної оптичної системи кожна лінія може розгля-

датися як сукупність точок, які накладаються одна на одну і при цьо-

му будуть зливатися в єдину цілу лінію. Це означає, що тонку підсві-

чену лінію можна зобразити у вигляді сукупності точок.

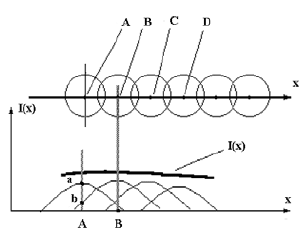
На рис. 1.8 наведені окремі світлові точки, а також сумарний

розподіл інтенсивності в зображенні лінії, яка поширюється вздовж

осі.

Рис. 1.8. Формування світлової лінії на основі масиву

світлових точок

Оскільки світлові коливання у всіх точках лінії некогерентні,

функцію розподілу інтенсивності в будь-якому перетині, перпендику-

лярному до лінії, можна отримати сумою усіх функцій розсіювання

точки (ФРТ), що знаходяться справа та зліва від перетину. Це означає,

хоча ФРТ не відповідає функції розсіювання лінії (ФРЛ), але поло-

ження максимумів цих функцій збігаються [56].

Максимум інтенсивності в поперечному перетину лінії зале-

жить від нахилу кривої функції розподілу аналогічно нахилу кривої

функції розподілу світлової плями та може бути визначений за допо-

могою інтенсивності сусідніх пікселів, в околі яких знаходиться спра-

вжній максимум.

Похибка дискретизації зображення, відповідно похибка відно-

влення неперервного поля за отриманими відліками залежить від та-

ких факторів: величина кроку дискретизації та спосіб відновлення не-

перервного поля, тобто від типу інтерполяційної функції [1, 4, 5].

На практиці, як правило, використовують прості в реалізації

способи відновлення, які є наближеними при будь-яких характеристи-

ках сигналу. Найчастіше використовують відновлення за допомогою

поліноміальної інтерполяції, при якій вхідне зображення та відновлене

збігаються у вузлах інтерполяції. При цьому вузлами є центри пікселів

з відповідним значенням інтенсивності.

У випадку використання простих типів інтерполяції, напри-

клад, несиметричної або симетричної, відновлення виконується з ве-

ликою похибкою. Існують і складніші інтерполяційні функції, але во-

ни не завжди дають виграш у точності.

Таким чином, для знаходження координат лінії вирішуються

такі ж задачі, що і для світлової плями. Це, в першу чергу, локалізація

максимуму та розподілу інтенсивності в поперечному перерізі в кож-

ній точці дискретизації з урахуванням впливу шумів.

Виходячи з вищенаведеного можна зробити висновок про не-

однозначність оцінки вимірювання піку світлової плями чи лінії у

зв’язку з дискретизацією зображення, а також наявністю шумів.

1.4. Класифікація методів крайового детектування

зображення об’єкта

Створення широкого спектра КОЕС спричинило адекватний

розвиток методів та засобів обробки зображень.

У розробку методів обробки зображень для вимірювальних за-

дач покладено праці Я. А. Фурмана, Л. П. Ярославського, В. П. Боюна,

І. С. Грузмана, Т. С. Хуанга, В. А. Сойфера, І. Б. Гуревича, Р. Дуди,

Б. К. Хорна, Б.П. Русина, Р. Гонсалеса, Р. Вудса, Л. І. Муравського.

Суттєвий внесок у формування і розвиток цих напрямків внесено пра-

цями А. Розенфельда, Г. Ендрюса, М. Бертеро, Ж. Понса, Д. Даджіона,

Р. Мерсеро, Д. Форсайта, Р. А. Воробеля, М. І . Шлезінгера, В. П. Ко-

жем’яко, У. Претта, І. Абду, Т. Павлідіса, Н. Берзінса, Л. Мітчела та

їхніми учнями, на теоретичне підґрунтя яких опираються подальші

дослідження.

Попередня обробка зображень є одним із основних етапів про-

цесу обробки та аналізу візуальної інформації. У багатьох випадках

інформативнішими є геометричні характеристики межі об’єктів цих

зображень – краї, які служать важливими ознаками для класифікації

зображених об'єктів і сприйняття зображення в цілому [7, 41, 50, 41,

57, 58].

Біологічні системи зорового сприйняття, як показують дослі-

дження, використовують, головним чином, обриси краю, а не поділ

об'єктів за яскравістю. Результатом крайового детектування або виді-

лення контуру зображення є побудова бінарного зображення, що міс-

тить його контури. Ця задача є багатогранною і на сьогодні може бути

розв’язана багатьма методами [1, 3, 4, 7, 54, 101, 103, 195, 196].

Для виділення контурів об’єктів на зображенні розроблено ба-

гато різних методів, які умовно відносять до таких основних класів:

методів високочастотної фільтрації; методів просторового диферен-

ціювання; методів функціональної апроксимації [59]. Така класифіка-

ція не відповідає сучасному розвитку методів крайового детектування

зображень й вимагає вдосконалення.

Загальним для всіх цих методів є прагнення розглядати межу як

область різкого перепаду функції інтенсивності зображення; відрізняє

ж їх математична модель, що вводиться, алгоритми пошуку примежо-

вих точок. Відповідно до поставлених задач до усіх алгоритмів кра-

йового детектування висувалися такі вимоги: виділені контури повин-

ні бути стоншеними; виділені контури повинні бути без розривів і за-

мкнутими. Однак висунуті вимоги не завжди виконуються й детекто-

ри не дають бажаного результату – у більшості випадків контури ви-

ходять незамкнутими і, як наслідок, непридатними для ряду процедур

аналізу. Таким чином, процес виділення контурів ускладнюється в

зв'язку з необхідністю використовувати декілька різних алгоритмів в

одному детекторі, що не дозволяє провести чіткі межі та віднести той

чи інший детектор до відповідного методу. У зв’язку з цим у роботі

запропоновано класифікацію методів крайового детектування, в осно-

ву якої покладено ідею поділу на методи, виходячи з основної опера-

ції чи процедури, що використовується детектором.

Розроблена класифікація методів крайового детектування

об’єктів на зображенні наведена на рис. 1.9.

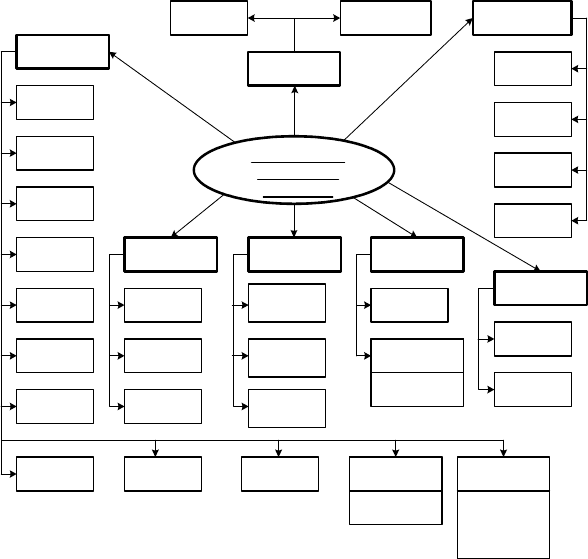
Усі підходи до побудови картини крайового детектування об'є-

ктів можна поділити на сім основних методів на основі [60]:

– компонент просторового диференціювання (КПД);

– коефіцієнтів порівняння з шаблоном (КПШ);

– просторової фільтрації (ПФ);

– статистичних підходів (СМ);

– визначення порогу (ПМ);

– перетворення простору інтенсивності (ППІ);

– моделі деформації (МД).

Крайові методи

детектування

зображення

Превітт

Робертса

Лапласа

Уоллеса

Лапласа-

Гаусса

(LOG)

Робінсона

Хюккеля

Бекера

Хука

Коніші

Превітт

Кірша

Ізотропні

Порівняння з

шаблоном

Статистич-

ний

Просторової

фільтрації

Просторового

диф-я

Собела

DOG

Детектори

кутів

Бедета

Форстнера

Харріса

Перетворення

простору

Детектори

кола

Сойка

Детектори

кола

Рада

Градієнтні

Лінійний

детектор

Порогові

Моделі

деформації

Багатомас

штабні

Пороговий

Гісто-

грамні

Дискремі-

нантні

Хафа

Довільної

форми

Параметрич-

но задані

Канні

Рис. 1.9. Класифікація методів крайового детектування об’єктів

Детектори на основі компонентів просторового диференці-

ювання

Методи КПД і КПШ оцінюють локальне значення градієнта або

його проекції у відповідному напрямку. Оператор градієнта можна роз-

глядати як лінійний фільтр зображення, який в областях різкої зміни

інтенсивності дає локальний максимум градієнта функції інтенсивності

та обчислюється за допомогою першої похідної. За означенням градієнт

зображення

(,)

в точці

(,)

– це вектор вигляду [7, 61-65]:

∂

⎡

⎤

⎢

⎥

⎡⎤

∂

⎢

⎥

∇= =

⎢⎥

∂

⎢

⎥

⎣⎦

⎢

⎥

∂

⎣

⎦

, (1.1)

де перша похідна в дискретному вигляді функції

()

визначається як

різниця значень інтенсивності сусідніх елементів:

(1) (

)

∂

=+−

∂

Аналогічно друга похідна визначається як різниця сусідніх

значень першої похідної:

(1) (1)2(

)

xfx f

∂

=++−−

∂

Важливу роль при знаходженні контурів має модуль вектора,

який визначається:

FGG∇=∇ = +

. (1.2)

Такі фільтри, як правило, задаються квадратною матрицею ко-

ефіцієнтів або маскою, що застосовується для кожної точки зображен-

ня. Розмір маски оператора або, інакше кажучи, його масштаб, може

бути

різним. Часто масштаб оператора градієнта, який дає в результаті

найкращу картину контурів об'єктів, підбирається шляхом експериме-

нтальних перевірок.

У випадку КПД задіяні дві маски, що визначає компоненти

градієнта у двох ортогональних напрямках, а у випадку КПШ кіль-

кість масок визначається необхідною точністю у визначенні розмірів

контуру й може доходити до 12 і більше.

Як методи КПШ, так і методи КПД можуть бути застосовані

для знаходження інших простих елементів зображення. Реалізацією

методу просторового диференціювання є відповідні градієнтні опера-

тори: перехресний оператор Робертса (Roberts' Cross operator), опера-

тор Собела (Sobel operator), метод Превітт (Prewіtt method) [66–68].

Оператор Робертса має високу швидкодію, але й високу чутли-

вість до шуму. Оператор Собела має відносно високу швидкість робо-

ти й стійкий до шуму. Метод Превітт характеризується високим сту-

пенем точності визначення краю об’єкта, стійкістю до шуму, але в той

же час має велику складність в обчисленні (у 8 разів більша в порів-

нянні з оператором Собела).

Для підкреслення перепадів інтенсивності зображення викори-

стовуються другі похідні. Двовимірний диференціальний оператор

називається оператором Лапласа і визначається з виразу:

∂

∇= +

∂

Лапласіан дуже чутливий до шуму, щоб зменшити цей вплив

часто використовують згладжування, наприклад, за методом Гаусса

. В

силу асоціативності операторів згортки використовують єдине ядро,

що має назву лапласіан гауссіана (Laplacіan of Gaussіan – LoG) і який

може бути попередньо обчислений за формулою [31]:

(,) 1

LoG x y e

πσ

−

⎡⎤

=− −

⎢⎥

⎣⎦

де

– стандартне відхилення оператора Гаусса.

Більше значення

потребує ширшої маски згортки, а отже бі-

льшого часу обробки. При цьому перший перехід через нуль LoG фу-

нкції досягається на

Детектор виявлення країв, що використовує лапласіан гауссіа-

на зі знаходженням точок перетину нульового рівня носить назву фі-

льтра Марра-Хілдрета (Zero crossіng detector, Marr edge detector) [53,

69, 70]. Цей детектор є більш ефективним, оскільки не вимагає додат-

кової інформації про характеристики інтенсивності зображення, а по-

хибка визначення краю, яка вноситься самим оператором за рахунок

дискретизації функції не перевищує 1 %. З іншого боку, недоліком

оператора є складність знаходження точок перетину нульового рівня,

що є основною проблемою методу, оскільки в загальному випадку це

задача, яка вимагає застосування більш складних методів [51, 53, 69].

Диференціальний оператор різниці гауссів (DOG) застосовує

маски меншої розмірності, зокрема 9×9 або 7×7 і може бути викорис-

таний як деяке наближення до LoG. DOG може бути описаний як

22 22

(,)

DoG x y

σσ

−−

=−

. (1.3)

Отже, DOG подається маскою, що є результатом віднімання

двох гауссових масок з

різними значеннями ступеня розмитості σ. Ві-

дношення σ

/σ

=1,6 з результатом найкращого наближення до LoG.

Одною з переваг DOG є можливість точного виявлення шири-

ни країв з різним значення σ

і σ

, а збільшення розмірності маски

призводить до виявлення більш широких країв.

Зображення, що зустрічаються на практиці, у більшості випад-

ків містять контури з різними швидкостями зміни інтенсивності, що

унеможливлює ефективно визначати всі існуючі на зображенні межі,

використовуючи лише оператор градієнта одного певного масштабу

[71]. У зв’язку з цим широко розвивається напрямок КПД, що дозво-

ляє побудувати картину контурів об'єктів зображення на основі інфо-

рмації, одержаної в результаті застосування оператора градієнта різ-

них масштабів. У літературі існує декілька підходів до аналізу багато-

масштабної інформації, тобто, до побудови картини контурів об'єктів

на основі градієнтних зображень різних масштабів [72, 73]. Існують

підходи, у яких аналіз градієнтних зображень проводиться від грубих

масштабів до точних, також існують підходи де аналіз виконується,

навпаки, від точних масштабів до грубих, і підходи, у яких аналіз не

залежить від послідовності розглядання зображень. Дані підходи різ-

няться й за принципами побудови градієнтного зображення одного

масштабу, тобто, видом застосовуваного оператора градієнта.

Однак недоліком такого підходу є можливий поділ контурів,

виділених при грубому масштабі, на декілька окремих при переході до

більш точного масштабу. Іншим недоліком таких підходів є значне