Білинський, Й.Й. Методи обробки зображень в комп’ютеризованих оптико-електронних системах: монографія

Подождите немного. Документ загружается.

2.4. Субпікселний метод локалізації краю зображення об’єкта

в міжпікселном просторі

Оскільки, примежова крива відтворюється за допомогою різної

кількості пікселів і з різним контрастом, то даний момент необхідно

враховувати при знаходженні крайової точки. Тому для подальших

викладок розглянемо ідеальний край у вигляді плоскої нахиленої схо-

динки інтенсивності, яка наведена на рис. 2.9 [3, 52–54, 61]. Такий

край елемента зображення можна описати декартовими координатами

з кутом нахилу

, амплітудою основи , контрастом і протяжністю

нахилу .

b h

Рис. 2.9. Модель краю

На підставі вищенаведеного встановлено, що в результаті низько-

частотного згладжування краю зображення формується сигнал перепаду

інтенсивності в області примежової кривої , який містить єдину

спільну точку з примежовою кривою вхідного сигналу . Це озна-

чає, що задача знаходження

краю примежової кривої зводиться до визна-

чення координати точки в області міжпікселного простору, яка є спіль-

ною примежових кривих згладжених зображень , і .

**( )H

*( )Hn

**(Hn)n )

Відомий метод визначення крайової точки, який базується на

знаходженні значення другої похідної, що відповідає нулю. Тоді ви-

значення спільної точки за допомогою запропонованого підходу може

бути подано як

*( ) **( )

Hn H n

∂

∂∂

. (2.23)

Таким чином, знаходження крайової точки розбивається на два

кроки: перший – виділення фрагмента, де знаходиться примежова

крива краю об’єкта вимірювання; другий – створення однонаправле-

ного низькочастотного фільтра з гауссовим ядром певних параметрів,

розмірністю вікна та направленістю; подальше виконання повторної

фільтрації в точках, що знаходяться в околі піксела з максимальним

значенням градієнта та знаходження спільної точки примежових кри-

вих [60, 133].

2.4.1. Аналіз процесу знаходження крайової точки на основі

низькочастотної фільтрації

В підрозділі 2.1 проведені математичні викладки та досліджен-

ня, які підтверджують що для знаходження крайової точки об’єкта

достатньо мати дві примежові криві, які отримані в результаті низь-

кочастотної фільтрації з різним параметром згладжування

. Для під-

твердження проаналізуємо процес знаходження крайової точки од-

новимірної дискретної примежової кривої з використанням реального

низькочастотного гауссового фільтра.

У результаті попередньої обробки зображення об’єкта на вхід

детектора подається одновимірний рядок сцени послідовності відліків

інтенсивності. Функцію перепаду інтенсивності вздовж рядка позна-

чимо

()

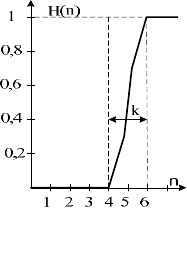
. Ця примежова крива, що містить k відліків, наведена на

рис. 2.10. Величина перепаду при цьому відповідає одиничному зна-

ченню.

Рис. 2.10. Ідеалізований перепад інтенсивності

На примежовій кривій будемо враховувати одне максимальне та

мінімальне значення, при якому

() 0Hn

() 1Hn

. Тому загальна

кількість відліків ідеального перепаду відповідно буде , а довжи-

на примежової кривої буде

2k +

[52, 84].

В аналітичному вигляді додатний перепад інтенсивності можна

подати як:

0 0, 1, 2, 3,...;

( ) 0,1,2,... ;

1 0,1,2,3,... .

при n

Hn hпри nl

при n

⎧

=−−−

⎪

⎨

⎪

⎩

Тоді від’ємний перепад інтенсивності за аналогією можна по-

дати як:

1 0, 1, 2, 3,...;

() 0,1,2,...;

0 1, 2, 3,... .

при n

Hn hпри nl

при nl l l

−

⎧

=−−−

⎪

⎨

⎪

=+ + +

⎩

Виконаємо фільтрацію примежової кривої в одновимірному

просторі за допомогою фільтра, що має мінімальну розмірність вікна в

3 піксели з довільно вибраними ваговими коефіцієнтами {1, 2, 1} та

знайдемо кількість ненульових відліків примежової кривої

У результаті ковзання цього вікна буде утворено ненульо-

вих і неодиничних відліки, а інтенсивність пікселів примежової кривої

буде змінена.

2k +

Виконаємо розрахунки крайової точки для примежової кривої,

наведеної на рис. 2.11.

Для цієї примежової кривої отримаємо:

( ) {(0;0;0,1), (0;0,1;0,2), (0,1;0,2;0,8), (0,2;0,8;0,9), (0,8;0,9;1), (0,9;1,1)}Hn=

26tk=+=

при ;

() 2( 1) ( 2)

() , 0,1,2,3,4,5

121

hn hn hn

Hn n

++ +

тоді значення відліку в результаті низькочастотної фільтрації

(0) 2 (1) (2) 0,1

(0) 0,025.

121 4

hhh

===

Аналогічним чином знаходяться решта відліків примежової

кривої .

(1) (5)HH−

Таким чином, примежова крива в результаті фільтрації отримає

такі відліки:

() {0;0,025;0,1;0,325;0,65;0,9,0,975;1}.Hn=

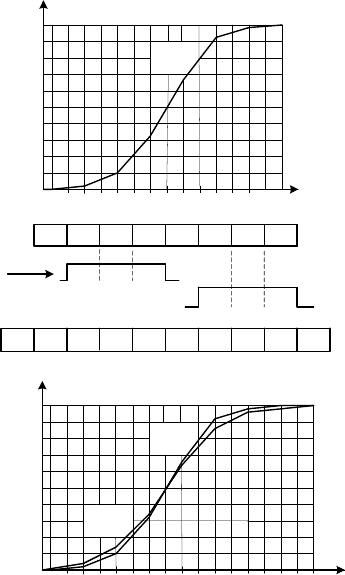
Рис. 2.11. До визначення спільної точки асиметричної примежової

кривої в результаті фільтрації

Сума усіх відліків даної характеристики дорівнює 1, тобто

()

−

∑

(2.24)

де k – розмірність вікна для однонаправленої маски; g(k) – вагові кое-

фіцієнти маски.

Проведені розрахунки означають, що для будь-якої асиметри-

нюєтьс

чної примежової кривої в результаті фільтрації загальна інтенсивність

пікселів, які входять до неї, залишається незмінною. Положення спі-

льної точки цих примежових кривих знаходиться на рівні 0,5 і не змі-

я при будь-яких значеннях вагових коефіцієнтів гауссового фі-

льтра при умові, коли розмірність вікна визначена (в даному випадку

дорівнює 3). Спільна точка перетину визначається як крайова.

Результати фільтрації квазіасиметричної примежової кривої за

допомогою гауссового фільтра з ваговими коефіцієнтами {1, 2, 1} на-

ведені на рис. 2.12.

H( n )

0,6

0,8

0,025

0,325

,65 0

,925

0,975

H( n )

0,2

0,4

0,6

0,8

0 123

Зсув

перше в

кно

останнє вікно

0,2

0,4

0 1

H*(n)

0, 006

,063

0,188 0,375

0,638

0,869

994

969

121

H*(n)

H**(n)

Рис. 2.12. До визначення краю казіасиметричної примежової кривої

Якщо примежова крива є квазіасиметричною, то результатом

фільтрації є крива, яка також має єдину спільну точку з вхідною, але

при цьому спостерігається відхилення координати краю від рівня 0,5.

Відліки отриманого перепаду в результаті фільтрації склада-

ють:

З цього виразу видно, що для такого фільтра сума усіх відліків

залишається незмінною, але асиметричність відліків порушується. У

випадку використання маски з іншими ваговими коефіцієнтами зна-

чення відліків змінюється. Це означає, що для знаходження крайової

точки в околі піксела з максимальним перепадом інтенсивності в ре-

зультаті виконання низькочастотної фільтрації можуть бути викорис-

тані лише ті відліки, які отримані в результаті попереднього встанов-

лення відповідних вагових коефіцієнтів, тобто гауссовий фільтр по-

винен мати адаптивний характер.

У результаті досліджень встановлено, що для проведення повтор-

ної фільтрації з метою знаходження крайової точки з мінімальною по-

хибкою гауссовий фільтр повинен будуватися на основі ступеня роз-

митості примежової кривої згідно з (2.20).

2.4.2. Математична модель краю зображення об’єкта в

міжпікселному просторі на основі поліноміальної інтерполяції

Для визначення крайової точки зображення об’єкта використаний

метод знаходження спільної точки двох примежо-

141].

терпол

ді таких векторів:

( ) {0; 0,006; 0,063; 0,188; 0,375; 0,638, 0,869; 0,994; 1}.Hn=

інтерполяційний

их кривих, отриманих у результаті низькочастотної фільтрації [139

Суть методу полягає в тому, що із вхідної та фільтрованої приме-

жової кривої вибирається k точок, за допомогою яких будуються ін-

яційні поліноми. З цією метою задаються вузли інтерполяції у

вигля

1, 1 2, 1

1,0 2,0

1,1 2,1

1,2 2,2

1, 2,

,, ,

−−

−Δ

+Δ

===

+Δ

NII

……



де

N – вектор координат точок зображення примежової кривої; Δ –

міжпікселний інтервал;

– вектор інтенсивності вхідної примежової

кривої;

– вектор інтенсивності фільтрованої примежової кривої;

j+2=k – кількість пікселів, що аналізуються.

Для визначення коефіцієнтів інтерполяційного полінома форму-

ється матриця

j,i

при умові, що N

j,I

= 1

()

() ()

nn n

−Δ −Δ −Δ

nn n



ji j

nn n

nj nj nj

+Δ +Δ +Δ



   



Коефіцієнти поліномів обчислюються за формулами:

(

)

1,1

jji

−

=NI N I

(2.25)

(

)

−

=NI N I

(2.26)

е a

і b

– коефіцієнти інтерполяційних поліномів для вхідної та філь-

трованої примежових кривих, відповідно.

В такому випадку примежові криві, тобто залежність інтенсивності

від номера піксела можна описати виразами:

() ( )

10121

nanaanan anfnI

==++++=

∑



() ( )

2012121

In bn b bnbn bn fnI

==++++=

∑



(2.28)

(2.27)

диться на перетині двох

полін

их перетинаються в точці С з

координатами (І

, n+δ), яка знаходиться в міжпікселному просторі та

відповідає краю зображення об’єкта.

Для знаходження субпікселної координати

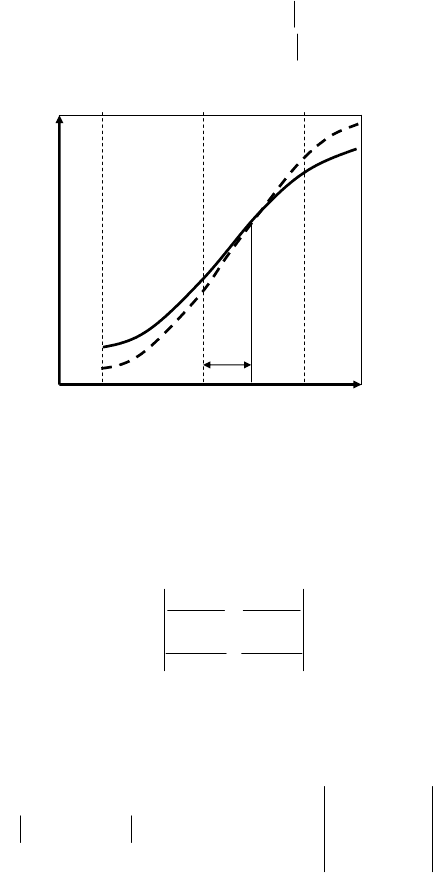
Крайова точка зображення об’єкта знахо

оміальних кривих (2.27) і (2.28), як наведено на рис. 2.13.

Поліноми I

(n) і I

(n) примежових крив

необхідне ви-

конання умови

(

)

(

)

In In

δ= +δ

{

}

(

)

,nfnIII+δ= =

з якої стає очевидним, що є розв’язком такої

системи:

(

)

()

fnI I

⎧

⎪

⎨

⎪

⎩

(2.29)

I(n)

n–Δ

n–

Рис. 2.13. Поліноміальні примежові криві в результаті фільтрації

та їхня спільна точка

Для розв’язання системи (2.29) скористаємося методом Ньютона

[142

–144]. Для цього складемо матрицю Якобі

(

)

(

)

()

11 11

22 22

nI f nI

JnI

nI f nI

∂∂

риця Якобі не вироджена, то розв’язок системи рівнянь

рентного виразу

∂∂

Якщо мат

(2.29) знайдемо з реку

()

(

)

()

fn I

−

212

ii i i

nI n I

nn JnI

fn I

−−

−

−−

−

+δ = +δ − ×

(2.30)

Ітераційний процес здійснюється доти, поки не буде виконана

умова

()

{}

()

{}

()

12 1 112

ii i i

nII I n I I I

−−

=≠

+δ − +δ ≤ε

де ε – похибка визначення.

Використовуючи математичну модель примежової кривої (2.16)

та (2.21), виконаємо розрахунок координати

крайової точки з відомим

значенням краю δ=0,9 та відомим значенням ступеня розмитості σ:

1; 1,25; 2, що відповідає максимальному перепаду інтенсивності між

сусідніми пікселами на кривій: 0,4; 0,35; 0,2 [145]. При цьому скорис-

таємося мінімальною кількістю точок, тобто k = 4, і визначимо век-

то

ри:

;

−

0,113

0,554

;

0,0055

0,931

0,204

0,04

,537

0,845

У результаті формування матриці вигляду

4, 4

4,4

1111

1000

1111

1248

−

За формулами (2.27) і (2.28) розрахуємо коефіцієнти й отрима-

ємо т

акі кубічні поліноми:

( ) 0,113 0,341 0,167 0,066 ;

nnn=+ + −

) 0,204 0,281 0,085 0,032

( .

nnn=+ + −n

Отриманий інтерполяційний поліном дає змогу знайти значен-

методом, але

й відомим, ня крайової точки не тільки запропонованим

тобто

Залежності абсолютної похибки знаходження субпікселної ко-

ординати від відомої координати краю для декількох примежових

кривих з різним ступенем розмитості при використанні поліномів тре-

тього, п’ятого та сьомого порядків, отриманих за допомогою моделі

примежової кривої (2.21 аведені на р . 2.14.

Результати, отримані запропонованим методом на основі ни-

зькочастотної фільтрації, порівнювались з відомим методом “перети-

ну нульового рівня”, який базується на знаходженні дискретної похі-

дної др

З графіків видно, що при ступені розмитості σ<2 доцільніше

використовувати поліном більш високого порядку, наприклад сьомо-

го, при значеннях ступеня розмитості σ≥2 відмінності в похибці зна-

ходження краю при використанні різних поліномів є незначними. При

цьому для примежових кривих, крайова точка яких відповідно дорів-

нює 0 або 0,5 міжпікселної ширини, абсолютна похибка є мінімаль-

ною.

об’єкта зображення запропонованим ме-

одом при декількох значеннях ступеня розмитості та відомим мето-

дом перетину ьового рівня.

Дослідження показали, що величина абсолютної похибки знахо-

дження

тотної фільтрації

має біл

знайти координату максимального значення першої похідної

та координату, що відповідає нулю другої похідної.

На підставі використання дискретної моделі примежової кри-

вої (2.21) було проведено моделювання знаходження субпікселної ко-

ординати з використанням інтерполяційних поліномів третього,

п’ятого та сьомого порядку в математичному пакеті Мathcad.

), н ис

угого порядку [69, 70].

У таблиці 2.1 наведені результати знаходження субпікселної

координати крайової точки

нул

крайової точки в межах ступеня розмитості 0<σ<1,8 на основі

низькочастотної фільтрації при використання інтерполяційних полі-

номів значно менша, ніж на основі методу «перетину нульового рів-

ня». Таким чином встановлено, що метод низькочас

ьш високу точність в порівнянні з методом нульового рівня та

може бути використаний для визначення геометричних параметрів

зображень об’єктів із ступенем розмитості в межах 0<σ 1,8. При

цьому відносна методична похибка не перевищує 10 %.