Blake A.J.(ed.) Crystal Structure Analysis
Подождите немного. Документ загружается.

342 X-ray and neutron sources
References
Clegg, W. (2000). J. Chem. Soc., Dalton Trans. 3223–3232.
Helliwell, J. R. (1998). Acta Crystallogr. A54, 738–749.
Piccoli, P. M., Koetzle, T. F. and Schultz, A. J. (2007). Comments Inorg.
Chem. 28, 3–38.
Wilson, C. C. (2000). Single crystal neutron diffraction from molecular
materials, World Scientific: Singapore.

A
Appendix A: Useful
mathematics and
formulae
Peter Main
A.1 Introduction
To paraphrase Lord Kelvin, when you cannot express your observations
in numbers, your knowledge is of a meagre and unsatisfactory kind.
The use of scientific observation to add to our knowledge inevitably
means we need to express both observations and deductions mathe-
matically. The link between the two is mathematical also. We present
here some mathematics and a few formulae that are important in X-ray
crystallography.
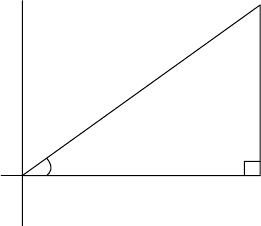
c
b
a
θ
Fig. A.1 A right-angled triangle for defin-
ing trigonometric ratios.
A.2 Trigonometry
Trigonometry means ‘measurement of triangles’, but its use goes far
beyond what its name suggests. Many properties of triangles can be
summarized in terms of the ratios of thesides ofthe right-angledtriangle
in Fig. A.1, giving:
cos θ = a/c sin θ = b/c tan θ = b/a
so that tan θ = sin θ/cos θ.
The symmetry of the sine and cosine functions shows that cos(−θ) =
cos(θ) and sin(−θ) =−sin(θ).
Another relationship among these functions is obtained from
Pythagoras’ theorem:
a
2
+ b
2
= c
2
giving cos
2
θ +sin
2
θ = 1.
343
344 Useful mathematics and formulae
Also useful in crystallography are the multiple angle formulae, which
are given without derivation as:
cos(θ +φ) = cos θ cosφ − sin θ sin φ
and sin(θ + φ) = sin θ cosφ + cos θ sin φ.
These come into their own in the manipulation of the electron-density
equation for numerical calculation. For example, by putting θ = 2π(hx+
ky) and φ = 2πlz in the above expressions, cos2π(hx + ky + lz) can be
changed into:
cos 2π(hx + ky + lz) = cos2π(hx + ky) cos 2π lz
− sin 2π(hx + ky) sin 2πlz.
A similar operation gives
cos 2π(hx + ky) = cos(2πhx) cos(2π ky) − sin(2π hx) sin(2πky)
sin 2
π(hx + ky) = sin(2πhx) cos(2π ky) + cos(2πhx) sin(2πky),
so that
cos 2π(hx + ky + lz) = cos(2πhx) cos(2πky) cos(2π lz)
− sin(2π hx) sin(2π ky) cos(2πlz)
− sin(2π hx) cos(2πky) sin(2πlz)
− cos(2πhx) sin(2πky) sin(2πlz).
It looks
as if we have made things far more complicated by doing
this. However, these expressions usually simplify enormously in dif-
ferent ways according to space group symmetry and are useful in the
Beevers–Lipson factorization of the electron-density equation, which is
how many computer programs handle Fourier transform summations.
r
imaginary
b
real
a
θ
Fig. A.2 The complex number a+ib plotted
on an Argand diagram.
A.3 Complex numbers
Much of the mathematics dealing with structure factors and discrete
Fourier transforms makes use of complex numbers. It is a pity these
numbers have the name they do, because it has the connotation of being
complicated. Complex numbers are simply numbers with two compo-
nents instead of the usual one. The components are called the real and
imaginary parts of the number and can be plotted on a two-dimensional
diagram, called an Argand diagram, as shown in Fig. A.2. The number
plotted has real and imaginary parts of a and b, respectively, and can be
written algebraically as a +ib where i
2
=−1. You may regard the imag-
inary constant i as a mathematical curiosity, but the important property
of its square given in the previous sentence enables complex numbers
to be multiplied and divided in a completely consistent way.
A.4 Waves and structure factors 345
An equivalent way to representa complex number is in polar form, i.e.
interms of r andθ inFig.A.2.These arecalled themodulusand argument
of the number respectively. A knowledge of trigonometry allows us
to write
a + ib = r cos θ + irsin θ = r(cos θ +i sin θ) = r e
iθ
.
The last relationship used in this equation is
cos θ + i sin θ = e
iθ
,
which is one of the most amazing relationships in the whole of mathe-
matics. Pythagoras’ theorem tells us that r
2
= a
2
+ b
2
and we also have
tan θ = b/a.
Some properties of complex numbers are important for the manip-
ulation of structure factors. A simple operation is to take the complex
conjugate, which means changing the sign of the imaginary part. Thus,
the complex conjugate of the complex number a+ib is written as (a+ib)
∗
and it is equal to a − ib. You should be able to confirm that multiplying
a complex number by its complex conjugate gives a real number that is
the square of the modulus:
(a + ib)(a + ib)
∗
= (a + ib)(a − ib)
= a
2
− iab+iab− i
2
b
2
= a
2
+ b
2
= r
2
.
A.4 Waves and structure factors
X-rays are waves and we must be able to deal with them mathematically.
The obvious wavy functions are sines and cosines, so these are used in
the mathematical description of waves. It is an enormous convenience
to combine both sines and cosines into the single term exp(iθ) as seen
in the last equation but one above. This is the main reason why you
find complex exponentials in the structure factor and electron-density
equations ((1.1) and (1.2), respectively, in Chapter 1).
Similarly, the structure factors F(hkl) are the mathematical represen-
tation of diffracted waves. When they are combined to form an image
of the electron density (which represents adding waves together), their
relative phases are important. The mathematical construction in Fig.A.2
allows both the amplitude of the wave, |F(hkl)|, and its relative phase,
φ(hkl), to be represented by the modulus and argument of a single com-
plex number. This leads us to write a structure factor in various ways
such as:
F(h) = A(h) + iB(h) =|F(h)|cos(φ(h)) + i|F(h)|sin(φ(h))
=|F(h)|exp(iφ(h)),
346 Useful mathematics and formulae
where the diffraction indices (hkl) are represented by the components of
the vector h.
The structure-factor equation, (1.1) in Chapter 1, shows that F(h) =
F
∗
(h), i.e. structure factors that are Friedel opposites are complex
conjugates of each other. This leads immediately to the relationship
F(h) × F(
h) =
|
F(h)
|
2
. In addition, we find that the product of any
two structure factors can be written as:
F(h) × F(k) =
|
F(h)
|
e
iφ(h)
×
|
F(k)
|
e
iφ(k)
=
|
F(h)F(k)
|
e
i(φ(h)+φ(k))
,
showing that the structure factor magnitudes multiply and the phases
add. This is of importance when applying direct methods of phase
determination.
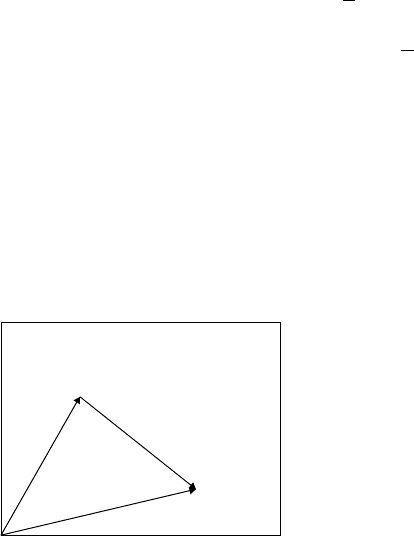
x
12
x
2
x
1
Fig. A.3 Addition of vectors: x
1
+x
12
= x
2
.
A.5 Vectors
A vector is often described as a quantity that has magnitude and direc-
tion, as opposed to a scalar quantity that has only magnitude. This
definition is sufficient for the present purpose and we shall see how
useful the directional properties of vectors are. One of the consequences
of this is that vectors can be added together as shown in Fig. A.3. The
vectors x
1
and x
12
are added together to give the resultant x
2
. This is
expressed algebraically as:
x
1
+ x
12
= x
2
.
Note that vectors are conventionally written in bold characters, as are
matrices when we come to them. If the vectors x
1
and x
2
give the posi-
tions of two atoms in the unit cell, they are known as position vectors;
x
12
is known as a displacement vector, giving the displacement of atom
2 relative to atom 1. A rearrangement of the above equation expresses
the displacement vector as x
12
= x
2
−x
1
and these displacement vectors
arise in the description of the Patterson function (see Chapter 9).
In the unit cell, the position vector x has components (x, y, z) such that
x=ax + by + cz,
where a, b and c are the lattice translation vectors (the edges of the unit
cell) and x, y and z are the fractional co-ordinates of the point. The vector
displacement of atom 2 from atom 1 can therefore be written as
x
12
= x
2
− x
1
= (ax
2
+ by
2
+ cz
2
) − (ax
1
+ by
1
+ cz
1
)
= a(x
2
− x
1
) + b(y
2
− y
1
) + c(z
2
− z
1
).
Similarly, the position of a point in reciprocal space is given by the vector
h, which has components (h,k,l) such that:
h = a*h + b*k +c*l,

A.6 Vectors 347
where a*, b* and c* are the reciprocal lattice translation vectors (the
edges of the reciprocal unit cell) and h, k and l are usually integers giving
the diffraction indices of the structure factor F(h) at that point in the
reciprocal lattice.
The scalar (dot) product of the two vectors x and h is:
h.x = hx + ky + lz,
which is an expression to be found in both the structure factor and
electron-density equations. The vector (cross) product is used in the
relationships between the direct and reciprocal lattices:
a
∗
=
b × c
V
b
∗
=
c × a
V
c
∗
=
a × b
V
V = a.b ×c,
where V is the volume of the unit cell. It should be remembered that
a × b = ab sin γ n,
where γ is the angle between the vectors and n is a unit vector perpen-
dicular to both a and b, such that a, b and n are a right-handed set. It
should be clear from these relationships that a* is perpendicular to the
bc-plane; similarly, b* and c* are perpendicular to the ac- and ab-planes,
respectively. If you need convincing that vectors are the most convenient
way of expressing these relationships, here is the volume of the unit cell
without using vectors:
V = abc
1 − cos
2
α − cos
2
β − cos
2
γ + 2 cos α cos β cos γ .
The angles of thereciprocal lattice canbe obtained from the relationships
above but, to save you the trouble, they are:
cos α
∗
=
cos β cos γ − cos α
sin β sin γ
,
with corresponding expressions for cos β* and cos γ * obtained by cyclic
permutation of α, β, and γ .
The calculation of a Bragg angle is commonly required, for example
to calculate structure factors or the setting angles on a diffractometer. In
the triclinic system, the formula is:
4 sin
2
θ
λ
2
= h
2
a
∗2
+ k
2
b
∗2
+ l
2
c
∗2
+ 2hka
∗
b
∗
cos γ
∗
+ 2klb
∗
c
∗
cos α
∗
+ 2lhc
∗
a
∗
cos β
∗
,
and this simplifies enormously for other crystal systems.
348 Useful mathematics and formulae
A.6 Determinants
Determinants feature in inequality relationships among structure
factors, are needed in matrix inversion, and form a useful diagnostic
tool when your least-squares refinement runs into trouble. A determi-
nant is a square array of numbers that has a single algebraic value. An
order two determinant is written and evaluated as:
ab
cd
= ad − bc,
and an order three determinant is:
abc
def
ghi
= aei + bfg + cdh − ceg −bdi − afh.
In general, a determinant can be expressed in terms of determinants
of order one less than the original. For an order n determinant, this is
expressed as
=
n
i=1
(−1)
i+j
a
ij
ij
,
where a
ij
is the ij element of and
ij
is the determinant formed from
by missing out the ith row and the jth column. The summation can
equally well be carried out over j instead of i and gives the same answer.
However, this is useful only for determinants of small order. Evalua-
tion of high-order determinants is best done using the process of Gauss
elimination (a standard mathematical procedure not discussed here) to
reduce the determinant to triangular form, then taking the product of
the diagonal elements.
A.7 Matrices
Matrices are used for a number of tasks in X-ray crystallography.
Typically, they represent symmetry operations, describe the orientation
of a crystal on a diffractometer, and are heavily used in the least-squares
refinement of crystal structures. A brief refresher course will therefore
not be out of place. A matrix is a rectangular array of numbers or alge-
braic expressions and matrix algebra gives a very powerful way of
manipulating them.
One of the operations often required is to transpose a matrix. This
exchanges columns with rows so that, if A is the matrix
⎛
⎝
ab
cd
ef
⎞
⎠
,
A.8 Matrices in symmetry 349
its transpose, A
T
,is
ace
bdf
.
If a square matrix is symmetric, it is equal to its own transpose.
Matrix multiplication is carried out by multiplying the elements in a
row of the first matrix by the elements in a column of the second and
adding the products. This forms the element in the product matrix on
the same row and column as those used in its calculation:
abc
def
⎛
⎝
ux
vy
wz
⎞
⎠
=
au + bv + cw ax + by + cz
du + ev + fw dx + ey + fz
Multiplication can only be carried out if the number of columns in the
first matrix is thesame as the numberof rowsin the second. For example,
you may wish to verify that
23
−14
3 −21
45−3
=
18 11 −7
13 22 −13
Multiplication of a matrix by its own transpose always produces a
symmetric matrix.
A.8 Matrices in symmetry
Matrix multiplication is useful for representing symmetry operations.
For example, the operation of the 2
1
axis relating (x, y, z)to(
1
/
2+x,
1
/
2−y,
−z) may be written as:
⎛
⎝
10 0
0 −10
00−1
⎞
⎠
⎛
⎝
x
y
z
⎞
⎠
+
⎛
⎝
1
/
2
1
/
2
0
⎞
⎠
,
and this form of expression is used to represent symmetry operations
in a computer.
It is sometimes useful to be able to deal with symmetry operations
in reciprocal space also. The operation above can be written in terms of
matrix algebra as
x
= Cx + d,
where C is the 3 ×3 matrix and d the translation vector. If a space group
symmetry operation is carried out on the whole crystal, by definition
350 Useful mathematics and formulae
the X-rays see exactly the same structure. The structure-factor equation
may then be written as
F(h) =
N
j=1
f
j
exp(2πih.(Cx
j
+ d) =
N
j=1
f
j
exp(2πih
T
Cx
j
) × exp(2π ih.d)
= F(h
T
C) exp(2π ih.d).
That is, the two reflections F(h) and F(h
T
C) are symmetry related. Their
magnitudes are the same and there is a phase difference between them
of 2πh.d.
This is easier to understand if we continue with the example above.
The 2
1
axis is one of those that occur in the space group P2
1
2
1
2
1
. The
symmetry-related reflections that it produces are given by
h
T
C =
hkl
⎛
⎝
10 0
0 −10
00−1
⎞
⎠
=
h
k l
.
That is, F(hkl) is related by symmetry to F(h
kl). Their magnitudes must
be the same and there is a phase shift between them of
2πh.d = 2π(hkl).(
1
/
2
1
/
2 0) = π(h + k).
Putting this all together gives the relationships |F(hkl)|=|F(h
kl)| and
φ(hkl) = φ(hkl) + π(h + k). Thus, the phase is the same if h + k is even,
but shifted by π if h +k is odd.
Even with anomalous scattering, these relationships are strictly true.
It is only when structure factors are related by a complex conjugate that
they are affected differently by anomalous scattering. For example, in
P2
1
2
1
2
1
, we have already seen that |F(hkl)| and |F(hkl)| are always the
same, but |F(hkl)| and |F(hkl)| will be affected differently, as will |F (hkl)|
and |F(hkl)|.
A.9 Matrix inversion
The inverse of the square matrix A is the matrix A
−1
that has the
property that
AA
−1
= A
−1
A = I,
where I is the identity matrix (1s down the diagonal and 0s every-
where else).
Operations performed by multiplying by a matrix, A, can be undone
by multiplying by the inverse of the matrix, A
−1
. For an order 2 square

A.10 Convolution 351
matrix, the recipe for inversion is:
if A =
ab
cd
then A
−1
=
1
det(A)
d −b
−ca
,
where det(A) is the determinant of the matrix A.
Inversion of an order three matrix is achieved by the following recipe:
if A =
⎛
⎝
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
⎞
⎠
, then form C =
⎛
⎝
c
11
c
12
c
13
c
21
c
22
c
23
c
31
c
32
c
33
⎞
⎠
, where c
ij
is the
determinant obtained from A by removing the ith row and jth column
and multiplying by (−1)
i+j
. We then have:
A
−1
=
1
det(A)
C
T
.
This recipe will work for any order of matrix, but it is extremely inef-
ficient for orders higher than three. Larger matrices are best inverted
using Gauss elimination, as mentioned earlier. It is a commonly believed
fallacy that matrix inversion is necessary for solving systems of linear
simultaneous equations. Since it is quicker to solve equations than to
calculate an inverse matrix, the inverse should be calculated only if it is
specifically required, for example, to estimate standard uncertainties of
parameters determined by the equations.
A.10 Convolution
Convolution is an operationthat affectsthe lives of allscientists. Since no
measuring or recording instrument is perfect, it will affect the quantity
that is detected before the recording takes place. For example, loud-
speakers change the signal that is fed to them from an amplifier, thus
altering (hopefully slightly) the sound that you hear. The mathematical
description of this is called convolution. It also appears in the mathemat-
ics of crystallography, although many people function quite adequately
as crystallographers without knowing much about it.
The simplest example of convolution is in the description of a crystal.
The convolution of a lattice point with anything at all, e.g. a single unit
cell, leaves that object unchanged. However, the convolution of two
lattice points with a unit cell gives two unit cells, one at the position
of each lattice point. A complete crystal, therefore, can be described as
the convolution of a single unit cell with the whole crystal lattice. This
would seem to be an unnecessary complication except for the intimate
association of convolution with Fourier transforms.
The convolution theorem in mathematics states that: “the Fourier
transform of a product of two functions is given by the convolution
of their respective Fourier transforms.” That is, if c(x), f(x) and g(x) are
Fourier transforms of C(S), F(S) and G(S), respectively, the theorem may
