Благовещенский С.Н., Холодилин А.Н. Справочник по статике и динамике корабля. Статика корабля. Том 1
Подождите немного. Документ загружается.

ствии
с изложенным правилом, ставят перед ординатами а и Ь в таблице и автомати-
чески
входят во все последующие расчеты, т. е. кубы отрицательных ординат — также
отрицательные (квадраты во всех случаях положительны) и при суммировании орди-
нат и кубов ординат вычисляют их алгебраические суммы.
При
пересечении вспомогательной ватерлинией шпангоута в четырех точках
(рис.
3.7, г) в соответствующую строку таблицы вписывают два значения входящих
ординат JA
X
И
]А
2
и два значения /б
х
и /В
а
выходящих ординат при сохранении та-
кого
же правила знаков.
В зависимости от положения ЦТ (точки /) может быть несколько комбинаций
знаков
двойных ординат.
'X /
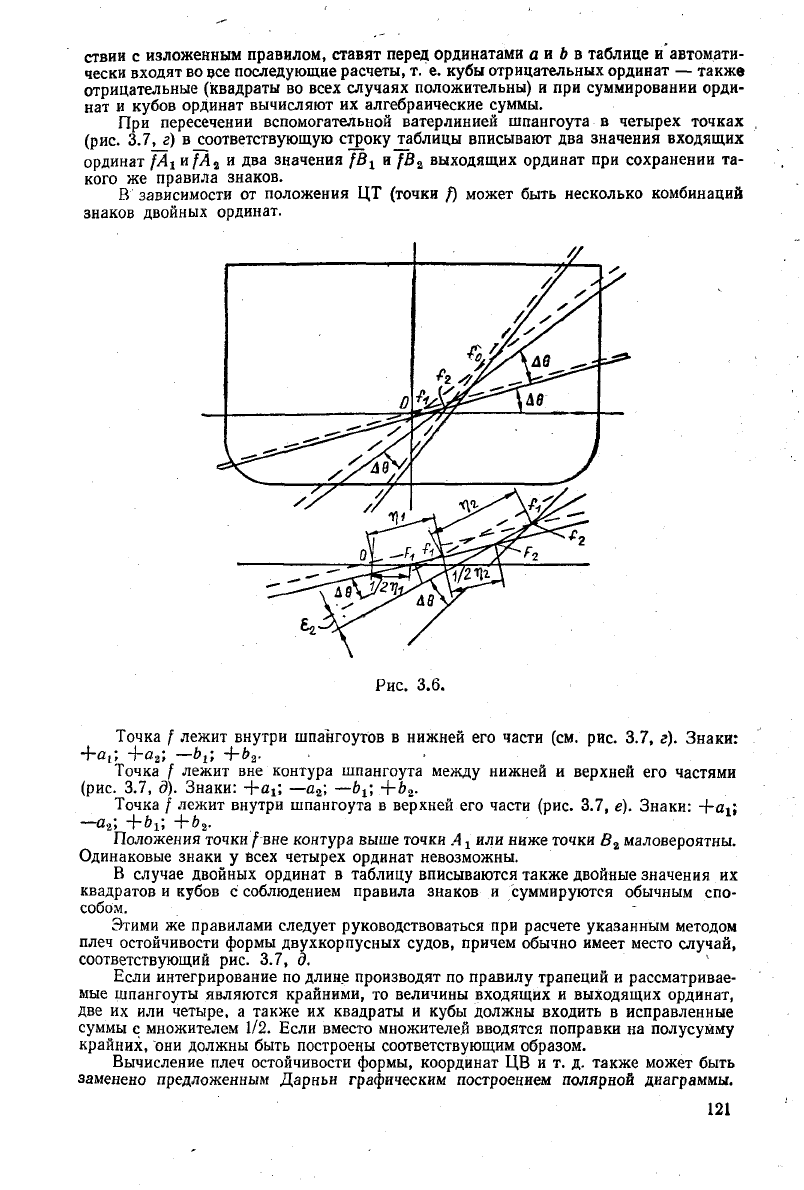
Рис.
3.6.
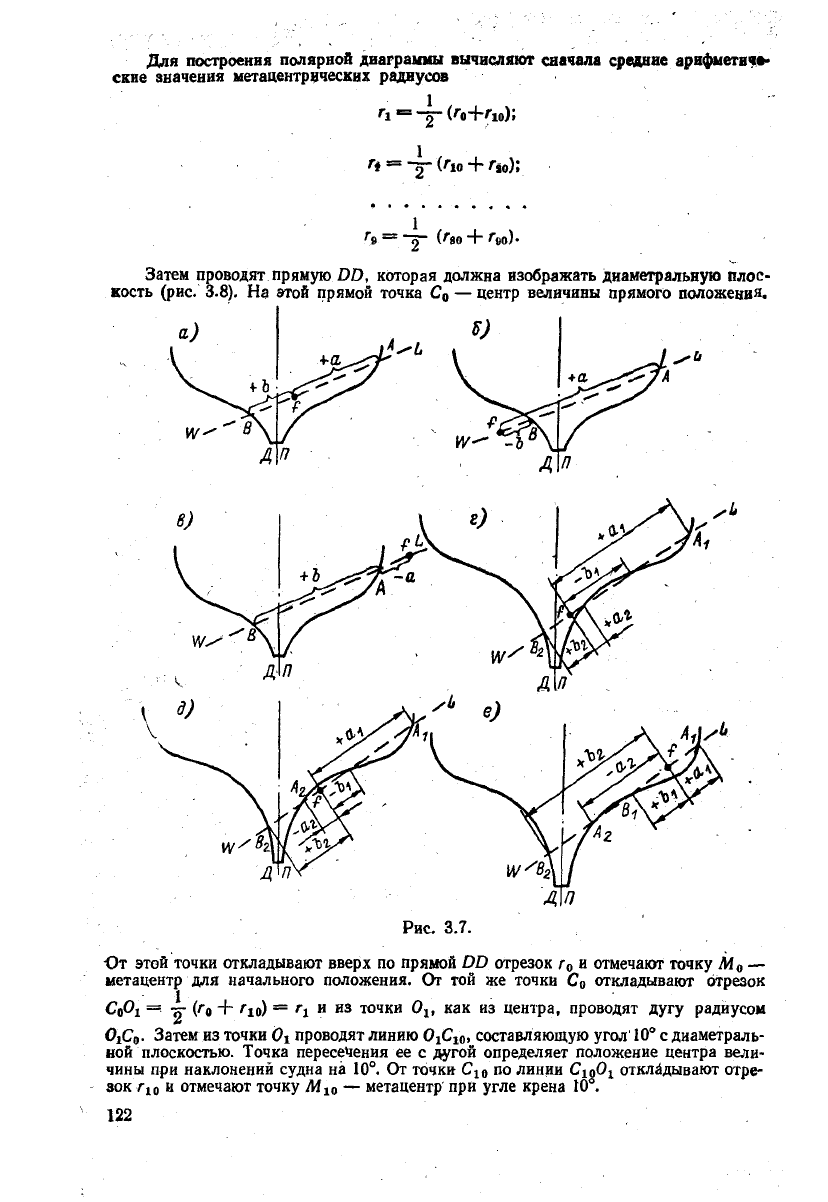
Точка
f лежит внутри шпангоутов в нижней его части (см. рис. 3.7, г).
Знаки:
х
;
+а
а
; —Ь
х
; +Ь
г
.
Точка
/ лежит вне контура шпангоута между нижней и верхней его частями
(рис.
3.7, д).
Знаки:
+fli', —а
2
; —Ь
х
; +6
2
-
Точка
/ лежит внутри шпангоута в верхней его части (рис. 3.7, е).
Знаки:
+aiJ
—a
2
; +&].; Л-Ь
2
.
Положения
точки/вне контура выше точки А
1
или ниже точки б
2
маловероятны.
Одинаковые
знаки у
Всех
четырех ординат невозможны.
В случае двойных ординат в таблицу вписываются также двойные значения их
квадратов и кубов с соблюдением правила знаков и суммируются обычным спо-
собом.
Этими
же правилами
следует
руководствоваться при расчете указанным методом
плеч остойчивости формы двухкорпусных судов, причем обычно имеет место случай,
соответствующий рис. 3.7, д. '-
Если
интегрирование по длине производят по правилу трапеций и рассматривае-
мые шпангоуты являются крайними, то величины входящих и выходящих ординат,
две их или четыре, а также их квадраты и кубы должны входить в исправленные
суммы с множителем 1/2. Если вместо множителей вводятся поправки на полусумму
крайних,
они должны быть построены соответствующим образом.
Вычисление плеч остойчивости формы, координат ЦВ и т. д. также может быть
заменено
предложенным Дарньи графическим построением полярной диаграммы.
121
Для построения полярной диаграммы вычисляют сначала средние арифметиче-
ские
значения метацентрических радиусов
Затем проводят прямую DD, которая должна изображать диаметральную плос-
кость (рис. 3.8). На этой прямой точка С
о
— центр величины прямого положения.
а)
АП
Рис.
3.7.
От этой точки откладывают вверх по прямой DD отрезок
/•„
и отмечают точку М
о
—
метацентр для начального положения. От той же точки С
в
откладывают отрезок
C<Pi
=
тг (
Л
о + ''ю) = г
х
и из точки 0
х
, как из центра, проводят
дугу
радиусом
OjCo- Затем из точки 0
Х
проводят линию
OiC
1B
,
составляющую
угол'
10° с диаметраль-
ной
плоскостью. Точка пересечения ее с
дугой
определяет положение центра вели-
чины
при наклонений судна на 10°. От
ТОЧКИ
С
10
ПО ЛИНИИ
0^0% откладывают отре-
зок
г
10
и отмечают точку М
10
— метацентр при
угле
крена 10 .
122
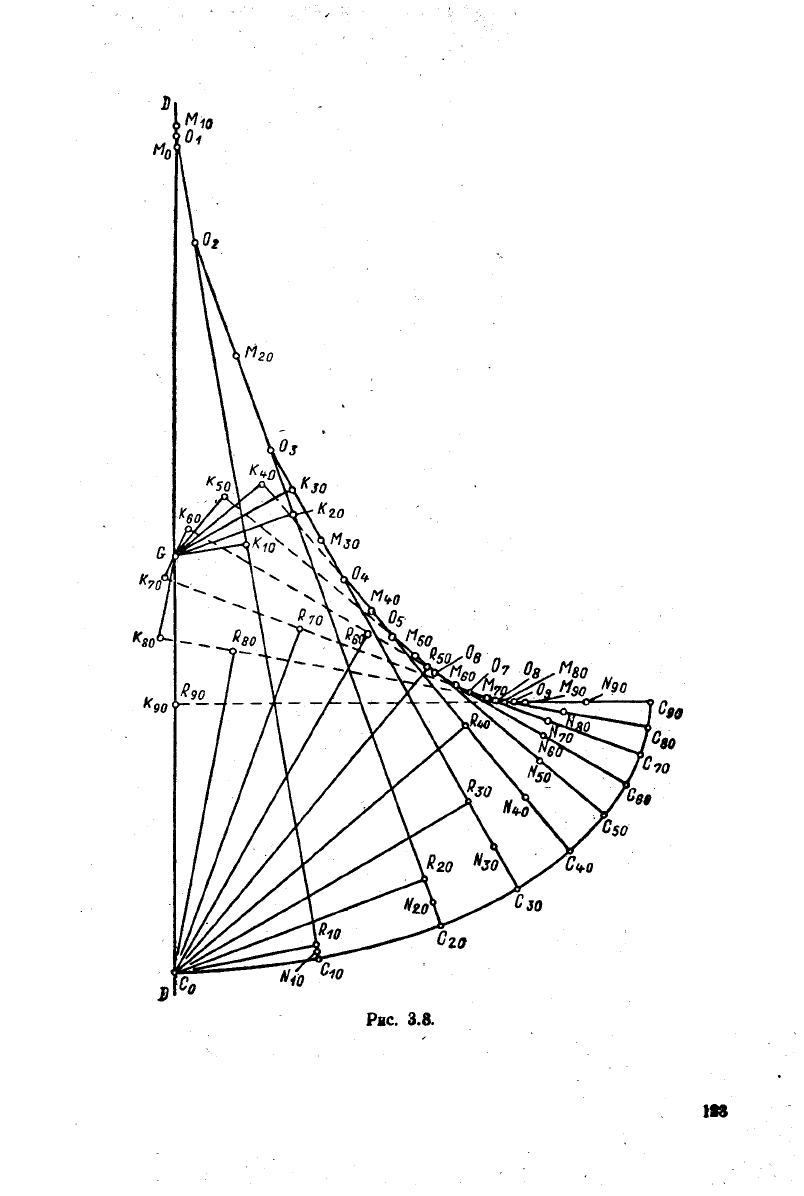
Рис.
3.8.
its

Далее,
от
этой
же
точки
С
10
откладывают отрезок
С
10
0
2
= г
2
= -5- (r
l0
+ г
!0
)
и
из
точки
О
г
, как из
центра, проводят
дугу
радиусом
г
г
и
прямую, составляющую
угол
20° с
диаметральной плоскостью. Точка
С
20
определяет положение центра вели-
чины
при
крене
20°.
Продолжая построение, находят положение центра величины
и
метацентра
для
следующих наклонений судна. Кривая, соединяющая точки
С
о
, С
10
,
С
20
и
С
зо
,— кривая центров величины; кривая, соединяющая точки
М —
метацентри-
ческая эволюта. Прямые
CQMQ
—
линии действия
сил
поддержания.
Опуская
из
точки
С
о
перпендикуляры
C
0
RQ
на
линии действия
сил
поддержания,
получают величины плеч остойчивости формы (/ф)
10
=
C
0
R
10
и т. д.
Откладывая
на
диаметральной плоскости отрезок
а= Zg — г
с
,
наносят точку
G
—
центр тяжести судна.
Из
точки
G
опускают перпендикуляры
G/CQ
на
линии дей-
ствия
сил
поддержания,
и
получают плечи остойчивости
О-Кю
= 'io!
G/C
2o
= /
2
o-
Отметив
на
линиях действия
сил
поддержания точки NQ
на
расстоянии
а от
точек
/Се» получают величины плеч динамической остойчивости
C
i0
N
20
=
(/
d
)
20
и т. д.
Возможен второй вариант расчета, предложенный
А. С.
Фишером. Согласно
этому варианту основной целью расчета является вычисление величин
/
м
(§ 35),
определяемых
по
формуле (3.13).
Вычисления целесообразно вести
по
схеме
треугольной табл.
3.4,
идея кото-
рой
была предложена
Р. А.
Матросовым.
В
таблице
в
имеет смысл верхнего предела
в
интеграле (3.13),
а ф —
текущая переменная
под
знаком этого интеграла, прини-
мающая значения
в
пределах
О ^ ф ^ 6 с
интервалом
10°.
Метацентрические
ра-
диусы
г
ф
вычислены
для
равнообъемных наклонений вторым способом
A. Hi
Крылова.
Для каждого значения
угла
ф
записывают разности
г
9
— г
0
= ДЛр. Для
значения
ф
= 0 Дг
ф
= 0.
Произведения
Дф cos (9 — ф)
вычисляют
раз
навсегда.
В
верхнюю
треугольную
часть таблицы записывают произведения
Дг
ф
- Дф cos (9 —
ф),
где Дг
ф
берут
соответ-
ственно данной строке,
а
величины
Дф cos (9 — ф)
берут
соответственно данному
столбцу
из
строки
II
таблицы. Значения
/
м
получаются
как
результат
суммирования
по
диагоналям чисел, стоящих
в
верхней треугольной части таблицы.
Схема табл.
3.4
может быть
с
успехом применена
и для
вычисления плеч остойчи-
вости формы /ф взамен схемы табл.
3.3,
если расчетчика
не
интересуют значения коор-
динат центра величины
и
метацентра.
Для
этого достаточно дополнить табл.
3.4
строкой
IV со
значениями
/•„
sin 9 (где
значения
9
берут
соответственно строке
I) и
строкой
V для
величины /ф
= /
м
+ 'о sin 9.
Вычисления плеча остойчивости
по
схеме
табл.
3.4 по
сравнению
с
другими
рас-
четными схемами более компактны
и
несколько более точны,
так как
связаны
с
мень-
шим
объемом промежуточных приближенных расчетов.
§
37.
ИНТЕРПОЛЯЦИОННЫЕ
КРИВЫЕ
ПЛЕЧ
ОСТОЙЧИВОСТИ
ФОРМЫ
Интерполяционные
кривые плеч остойчивости формы
служат
для
быстрого
вы-
числения
диаграммв1 статической остойчивости
при
различных вариантах нагрузки.
Для построения интерполяционных кривых достаточно произвести расчет плеч
остойчивости формы
не
менее
чем при
трех
значениях водоизмещения, которые
бе-
рутся
в
пределах
от
водоизмещения судна порожнем
до
водоизмещения полного
погружения водонепроницаемого объема судна
под
воду.
Величина водоизмещения
полного погружения
V
n
может быть определена
по
масштабу Бонжана, если
он вы-
числен
для
полных площадей шпангоутов
от
основной линии
до
верхней палубы.
Определив водоизмещение судна порожнем
V
o
и
полного погружения
V
n
,
устанавли-
вают промежуточные водоизмещения
V
lt
V
2
и т. д. и,
отметив
для
каждого
из них на
корпусе соответствующие осадки, производят расчет плеч остойчивости формы любым
способом
(§ 36).
Затем строят график интерполяционных кривых плеч остойчивости
124
формы,
откладывая по оси абсцисс водоизмещения V{, а по оси ординат — соответ-
ствующие им значения плеч остойчивости формы /ф для каждого наклонения судна.
Соединяя
концы ординат плавными кривыми, получают серии кривых, число которых
равно числу наклонений (рис. 3.9).
При
значении V = V
n
все кривые пересекают ось абсцисс. Чтобы рассчитать
диаграмму статической остойчивости, нужно для заданного случая нагрузки опреде-
лить водоизмещение и возвышение
центра тяжести над центром величины
а=
Ч —
г
с
..
Ординаты диаграммы статической
остойчивости определяют по формуле
k
= /ф — a sin в,
где величину /ф снимают с интерполя-
ционных кривых.
Для повышения точности построе-
ния
интерполяционных кривых реко-
мендуется воспользоваться дополни-
тельными несложными построениями,
которые
дают
направления касатель-
ных к кривым в расчетных точках.
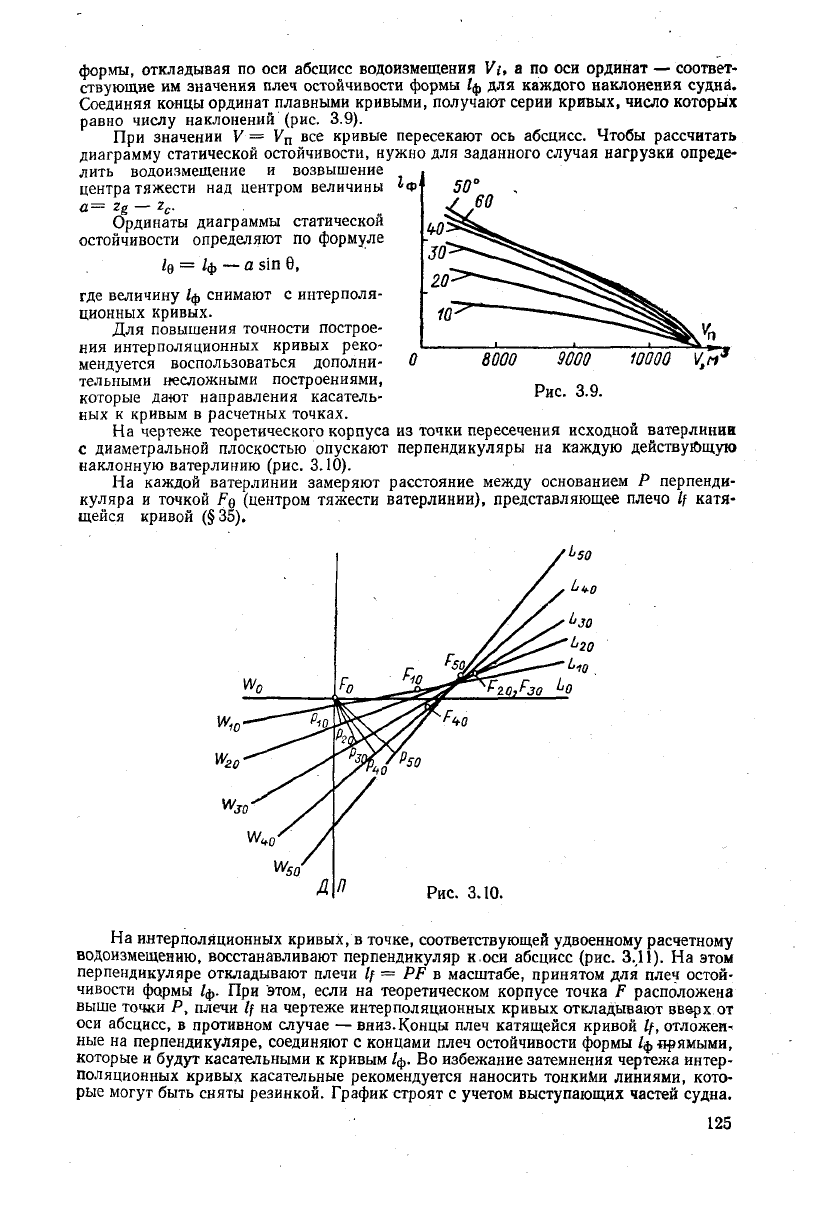
На
чертеже теоретического корпуса из точки пересечения исходной ватерлинии
с диаметральной плоскостью опускают перпендикуляры на каждую действующую
наклонную ватерлинию (рис.
3.10).
На
каждой ватерлинии замеряют расстояние
между
основанием Р перпенди-
куляра и точкой FQ (центром тяжести ватерлинии), представляющее плечо If катя-
щейся кривой (§35).
10
8000
9000
Рис.
3.9.
10000
V.ti'
w.
'•so
W,
'so
ДП
Рис.
3.10.
На
интерполяционных кривых, в точке, соответствующей удвоенному расчетному
водоизмещению, восстанавливают перпендикуляр к.оси абсцисс (рис.
3.11).
На этом
перпендикуляре откладывают плечи If — PF в масштабе, принятом для плеч остой-
чивости формы /ф. При этом, если на теоретическом корпусе точка F расположена
выше точли Р, плечи // на чертеже интерполяционных кривых откладывают вверх от
оси абсцисс, в противном
случае
—
вниз.
Концы
плеч катящейся кривой If, отложен-
ные на перпендикуляре, соединяют с концами плеч остойчивости формы /ф-прямыми,
которые и
будут
касательными к кривым /ф. Во избежание затемнения чертежа интер-
поляционных кривых касательные рекомендуется наносить тонкими линиями, кото-
рые
могут
быть сняты резинкой. График строят с учетом выступающих частей судна.
125
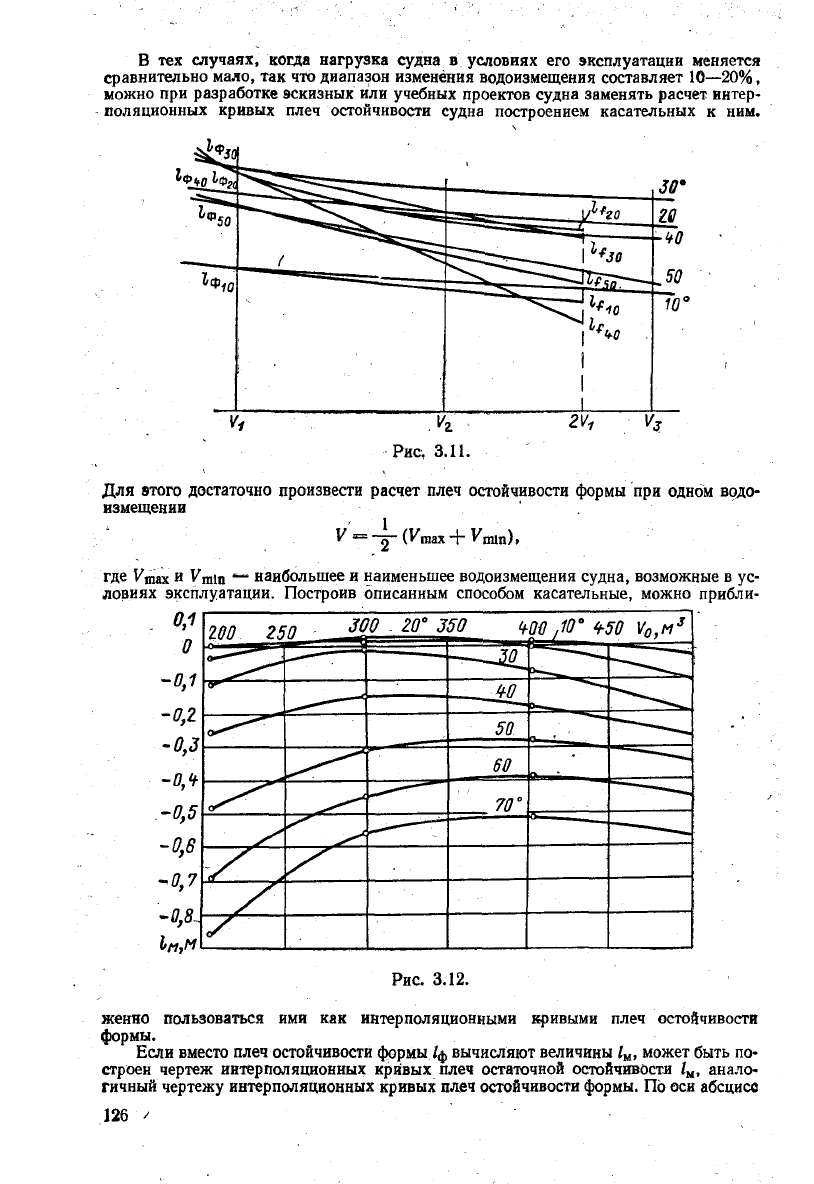
В тех
случаях,
когда нагрузка судна в условиях его эксплуатации меняется
сравнительно мало, так что диапазон изменения водоизмещения составляет
10—20%,
можно при разработке эскизных или учебных проектов судна заменять расчет интер-
поляционных
кривых плеч остойчивости судна построением касательных к ним.
Для этого достаточно произвести расчет плеч остойчивости формы при одном водо-
измещении
'
где
Ушах
и
V
m
i!i""
наибольшее и наименьшее водоизмещения судна, возможные в ус-
ловиях эксплуатации. Построив описанным способом касательные, можно прибли-
Рис.
3.12.
женно пользоваться ими как интерполяционными кривыми плеч остойчивости
формы.
Если вместо плеч остойчивости формы /ф вычисляют величины /
н
, может быть по-
строен чертеж интерполяционных кривых плеч остаточной остойчивости /
м
, анало-
гичный
чертежу
интерполяционных кривых плеч остойчивости формы. По оси абсцисо
126
^

графика откладывают величины водоизмещения V, а по оси ординат — соответствую-
щие величины 1„ для данного постоянного
угла
крена. Значения /„
могут
быть как
Положительные, так и отрицательные. Плавные кривые, соединяющие построенные
таким образом для данного
угла
крена точки, и
будут
интерполяционными кривыми
L.
(рис.
3.12).
v
Плечи
статической остойчивости при заданном водоизмещении V и метацентриче-
ской
высоте h определяют по формуле
/ = l
H
+ h sin в,
где /
м
— снимают с графика.
При
водоизмещении V
n
, соответствующем полному погружению судна, все кри-
вые 1
М
пересекают ось абсцисс. В целях контроля вычислений и построений можно
в
сомнительных точках построить контрольные касательные к кривым 1
и
согласно
выражению
dV
Контрольную касательную строят аналогично тому описанию, которое было при-
ведено для кривых 1ф. Однако из-за присутствия в формуле трудно определяемого
радиуса кривизны к
0
катящейся кривой If в прямом положении судна построение
контрольной
касательной в данном
случае
получается менее точным.
§ 38.
РАСЧЕТ
ОСТОЙЧИВОСТИ НА БОЛЬШИХ УГЛАХ
КРЕНА С ПОМОЩЬЮ ИНТЕГРАЛЬНЫХ КРИВЫХ
Описываемый способ расчета не
требует
построения равнообъемных ватерлиний.
Для каждого шпангоута рассчитывают и строят интегральные кривые погруженных
площадей шпангоутов и их статических моментов в функции от глубины погружения
при
ряде значений
угла
крена Э = 10°, 20°, 30° и т. д. Для этого на диаметральной
Рис.
3.13.
плоскости теоретического корпуса выбирают произвольную точку Р на расстоянии
gp от основной плоскости, принимаемую За след оси Рх — оси вращение судна —'и
именуемую полюсом. Далее на прозрачной кальке вычерчивают сетку расчетных ва-
терлиний судна и перпендикулярную к ним линию Л£ (рис.
3.13).
Кальку с сеткой
ватерлиний накладывают на чертеж корпуса так, чтобы линия А% проходила через
полюс Р и составляла с диаметральной плоскостью
угол
6, а самая нижняя ватерли-
127
ния
Аг\ касалась бы обвода того шпангоута, для которого вычисляют интегральные
кривые.
Далее измеряют расстояние РА от полюса до касательной к обводу шпангоута
ватерлинии
и обозначают через 7\е. Затем измеряют входящие ординаты у
1
шпан-
гоута
и выходящие у
г
по каждой ватерлинии и вычисляют ординаты интегральных
кривых
ш,е
и
Щъ по
схеме
вычисления интеграла с верхним переменным пределом
(3.25)
(3.26)
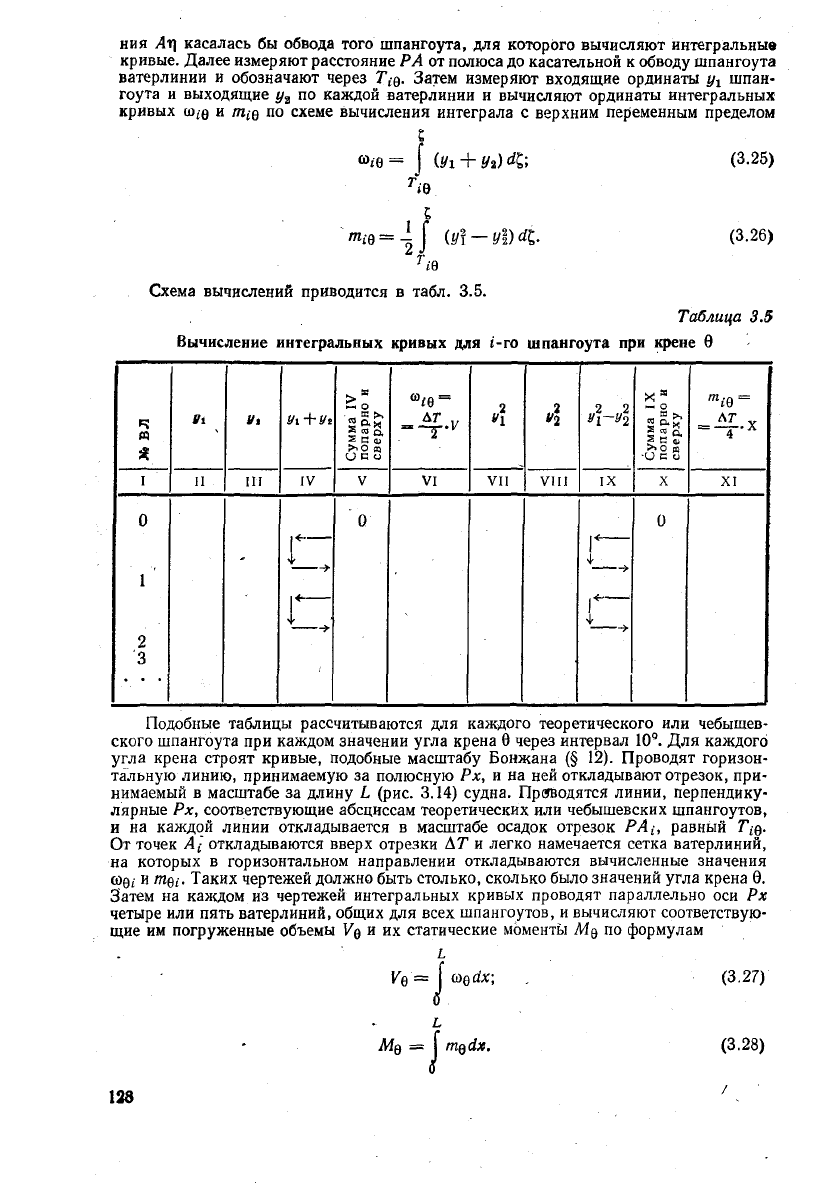
Схема вычислений приводится в табл. 3.5.
Таблица
3.5
Вычисление интегральных кривых для (-го шпангоута при крене 0
ч
I
0
1
2
'3
Si
и
У,
III
-
Vl+Уг
IV
г—
Сумма
IV
попарно
и
сверху
V
0
VI
Л
VII
4
VIII
У\~У\
IX
<
4-
1"
,
Сумма
IX
попарно
и
сверху
X
0
-—•X
XI
Подобные
таблицы рассчитываются для каждого теоретического или чебышев-
ского
шпангоута при каждом значении
угла
крена 6 через интервал 10°. Для каждого
угла
крена строят кривые, подобные масштабу Бонжана (§ 12). Проводят горизон-
тальную линию, принимаемую за полюсную Рх, и на ней откладывают отрезок, при-
нимаемый
в масштабе за длину L (рис. 3.14) судна. Проводятся
линии,
перпендику-
лярные
Рх, соответствующие абсциссам теоретических или чебышевских шпангоутов,
и
на каждой линии откладывается в масштабе осадок отрезок РА;, равный TJ-Q.
От точек А\ откладываются вверх отрезки AT и легко намечается сетка ватерлиний,
на
которых в горизонтальном направлении откладываются вычисленные значения
«е,- и
Ш(ц.
Таких чертежей должно быть столько, сколько было значений
угла
крена 0.
Затем на каждом из чертежей интегральных кривых проводят параллельно оси Рх
четыре или пять ватерлиний, общих для
всех
шпангоутов, и вычисляют соответствую-
щие
им погруженные объемы VQ
И ИХ
статические моменты MQ
ПО
формулам
(3.27)
L
• I
пщйх.
(3.28)
138
Вычисление интегралов должно производиться по принятому правилу прибли-
женного интегрирования (§ 4), причем можно применять и правило Чебышева.
Расстояние линии действия силы поддержания от вертикальной плоскости PZ, (см.
рис.
3.18) равно
/*
= ^.
(3.29)
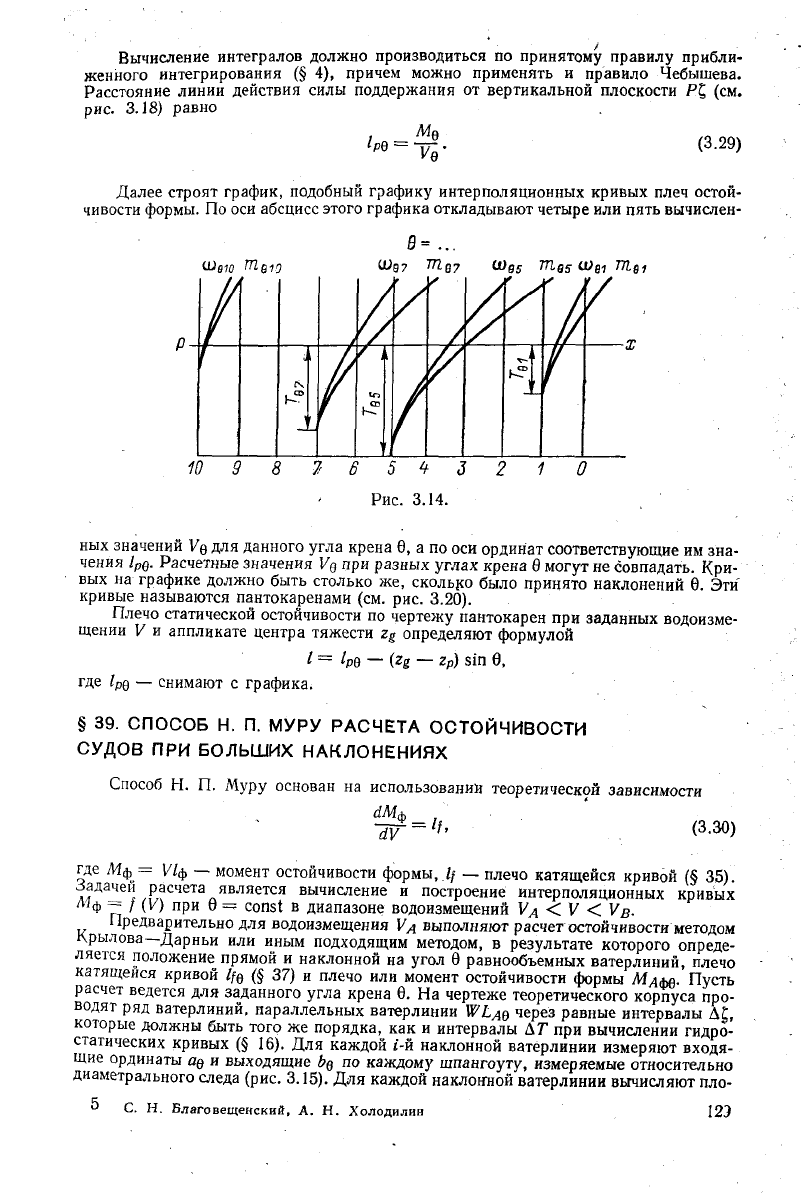
Далее
строят график, подобный графику интерполяционных кривых плеч остой-
чивости формы. По оси абсцисс этого графика откладывают четыре или пять вычислен-
10 9
ных значений VQ
ДЛЯ
данного
угла
крена 9, а по оси ординат соответствующие им зна-
чения
1р
в
. Расчетные значения VQ при разных
углах
крена 9
могут
не совпадать. Кри-
вых на графике должно быть столько же, сколько было принято наклонений 9. Эти
кривые называются пантокаренами (см. рис.
3.20).
Плечо статической остойчивости по
чертежу
пантокарен при заданных водоизме-
щении
V и аппликате центра тяжести Zg определяют формулой
I
===
ipQ — {zg — zp) sin 9,
где 1
P
Q — снимают с графика.
§
39.
СПОСОБ Н. П. МУРУ РАСЧЕТА ОСТОЙЧИВОСТИ
СУДОВ
ПРИ БОЛЬШИХ НАКЛОНЕНИЯХ
Способ Н. П.
Муру
основан на использовании теоретической зависимости
ir
=
'
f>
(з.зо)
где Мф = V/ф — момент остойчивости формы, Ц — плечо катящейся кривой (§ 35).
Задачей расчета является вычисление и построение интерполяционных кривых
"п
П
'
)И
^
cons
*
; в
Диапазоне водоизмещении V
A
< V < VB-
Предварительно для водоизмещения V
A
выполняют расчет остойчивости методом
Крылова—Дарньи или иным подходящим методом, в
результате
которого опреде-
ляется положение прямой и наклонной на
угол
9 равнообъемных ватерлиний, плечо
катящейся кривой //
е
(§ 37) и плечо или момент остойчивости формы
М
Афв
.
Пусть
расчет ведется для заданного
угла
крена 9. На
чертеже
теоретического корпуса про-
водят ряд ватерлиний, параллельных ватерлинии
WL
A
Q
через равные интервалы ДС,
которые должны быть
того
же порядка, как и интервалы ДГ при вычислении гидро-
статических кривых (§ 16). Для каждой t-й наклонной ватерлинии измеряют входя-
щие ординаты а
е
и выходящие 6
0
п
° каждому шпангоуту, измеряемые относительно
диаметрального
следа
(рис.
3.15).
Для каждой наклонной ватерлинии вычисляют пло-
5 С. Н. Благовещенский, А. Н. Холодилин 12Э
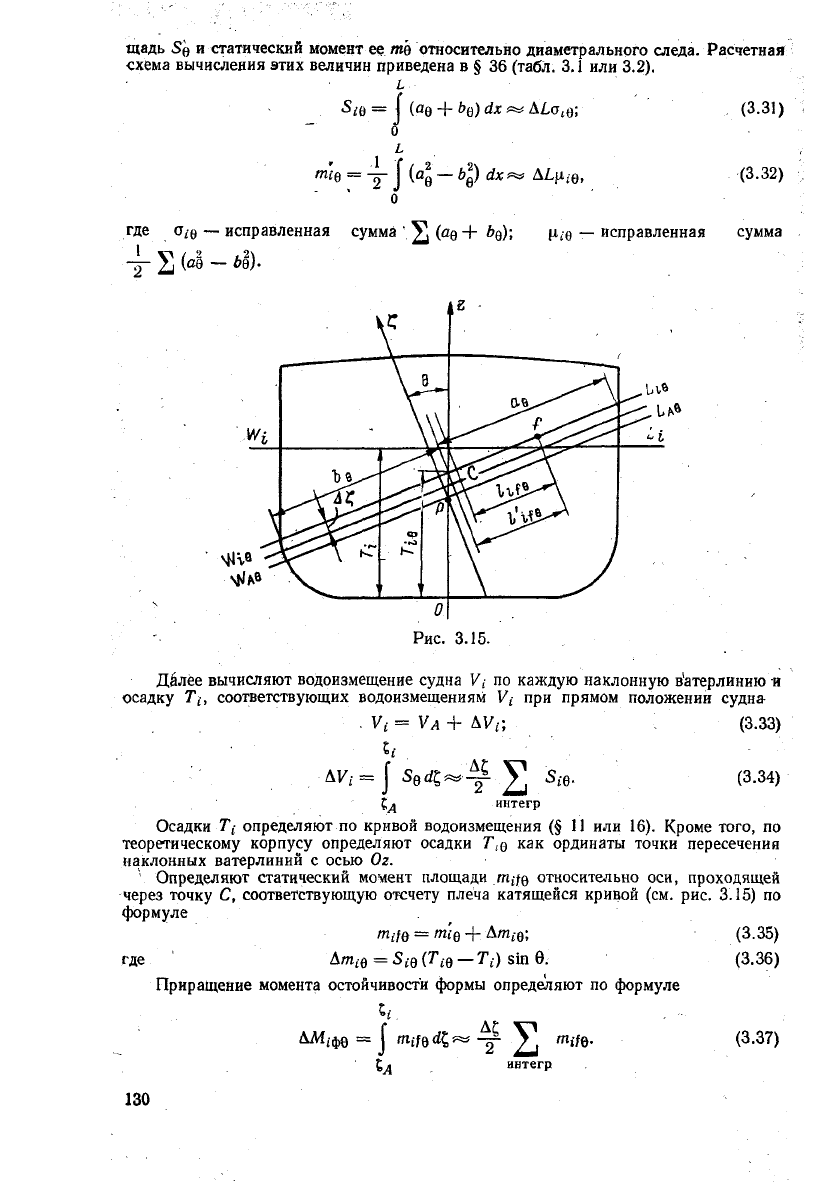
щадь S'o и статический момент ее гае относительно диаметрального следа. Расчетная
схема вычисления этих величин приведена в § 36 (табл. 3.1 или 3.2).
L
L
1
( , 2
mia
= -j- J (a
e
—
I
AZ.a,e;
(3.31)
(3.32)
где a
ie
— исправленная сумма ".Jj (
a
9+ *e); И-.е — исправленная сумма
ДЙлёе вычисляют водоизмещение судна Vi по каждую наклонную в'атерлинию и
осадку T
h
соответствующих водоизмещениям V,- при прямом положении судна-
. V[ = VA + AVr,
(3.33)
S(e-
(3-34)
Ёд интегр
Осадки
Т(
определяют
по
кривой водоизмещения
(§ 11 или 16).
Кроме того,
по
теоретическому корпусу определяют осадки
T,Q как
ординаты точки пересечения
наклонных
ватерлиний
с
осью
Ог.
х
Определяют статический момент площади
/п,/е
относительно
оси,
проходящей
через точку
С,
соответствующую отсчету плеча катящейся кривой
(см. рис. 3.15) по
формуле
nitfe
= m'i
6
+
Дт,-
в
;
(3.35)
где &m
ie
= Sce(T
ie
—Тс) siu в: (3.36)
Приращение
момента остойчивости формы определяют по формуле
AAf/фв
=
(3.37)
интегр
130
