Благовещенский С.Н., Холодилин А.Н. Справочник по статике и динамике корабля. Статика корабля. Том 1
Подождите немного. Документ загружается.

где л
ф
—метацентрический радиус-судна, накрененного
на
угол
ф,
равный"
In,
г
ч>
==
~
(3.2)
Здесь
/т —
момент инерции площади наклонной ватерлинии относительно
ее цен-
тральной продольной
оси.
Плечи
статической остойчивости определяются общей формулой
/
е
= У cos 6 + г sin в — a sin 6, (3.3)
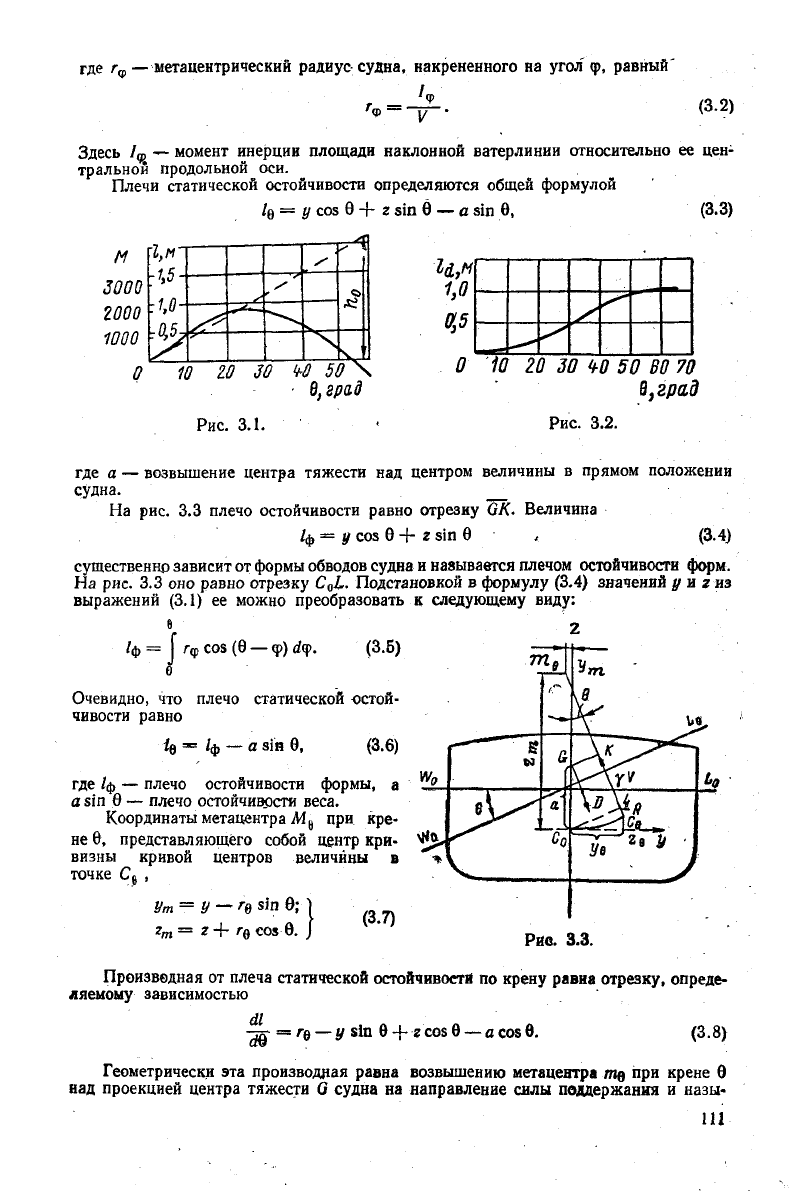
М
зооо
2000
1000
о
1,м
-10-
>*
S,
1,0
'
10
ZO 30 bO 50 N
•
в,град
Рис.
3.1.
0
10 ZO 30
Ц-0
50 BO 70
8
}
град
Рис.
3.2.
где
а —
возвышение центра тяжести
над
центром величины
в
прямом положении
судна.
На
рис. 3.3
плечо остойчивости равно отрезку
GK.
Величина
/ф ==
у cos 9 + г sin 9 , (3.4)
существенно зависит
от
формы обводов судна
и
называется плечом остойчивости форм.
На
рис. 3.3 оно
равно отрезку
С
о
£.
Подстановкой
в
формулу
(3.4)
значений
у и г из
выражений
(3.1) ее
можно преобразовать
к
следующему
виду:
1
=
Ар cos (9 — <р) dip.
(3.5)
Очевидно,
что
плечо статической остой-
чивости равно
h
=•=
/ф
— a sis 9, (3.6)
где /ф
—
плечо остойчивости формы,
а
a
sin 9 —
плечо остойчивости веса.
Координаты метацентра
М
е
при кре-
не
в,
представляющего собой центр
кри-
визны
кривой центров величины
в
точке
С
л
,
,
= у — г
%
sin 9;
:
= ? 4" Га
COS
9.
(3.7)
Рис.
3.3.
Производная
от
плеча статической остойчивости
по
крену
равна отрезку, опреде-
ляемому
зависимостью
•^g.
= г
е
— у sin
— acosB.
(3.8)
Геометрически
эта
производная равна возвышению
метацентра
т%
при
крене
9
над проекцией центра тяжести
G
судна
на
направление силы поддержания
и
назы-
111

вается обобщенной метацентрической высотой. На рис. 3.3 она равна отрезку т$К.
Очевидно, что значение производной от
1$
в начале координат равно
„-~-Н.
. (3.9)
Производная
от плеча остойчивости формы по водоизмещению определяется вы-
ражением
—тгг
= -п-(Н — Ш- (J.1U)
dv V
Величина If (см. рис. 3.4) называется плечом катящейся кривой и равна расстоя-
нию
fp
между
центром тяжести / площади наклонной равнообъемной ватерлинии
~~ " i и проекцией р точки пересечения исходной ватерлинии с диаметральной пло-
•
а
скостью на наклонную ватерлинию. Отрезку Ц
приписывается знак плюс, если точка / распола-
гается от точки р в сторону наклонения и, следо-
0
вательно, на рис- 3.4 If > 0.
х
^ Производная от плеча статической остончи-
р If J вости по водоизмещению при неизменном поло-
жении
центра тяжести равна
г. о л
~.JS~
==
Tr(
z
w
s
'
n
^ + h — 'ф)> (311)
Рис.
3.4. dV у -
где Зщ, — погружение центра величины под ватерлинию в прямом положении судна.
Можно
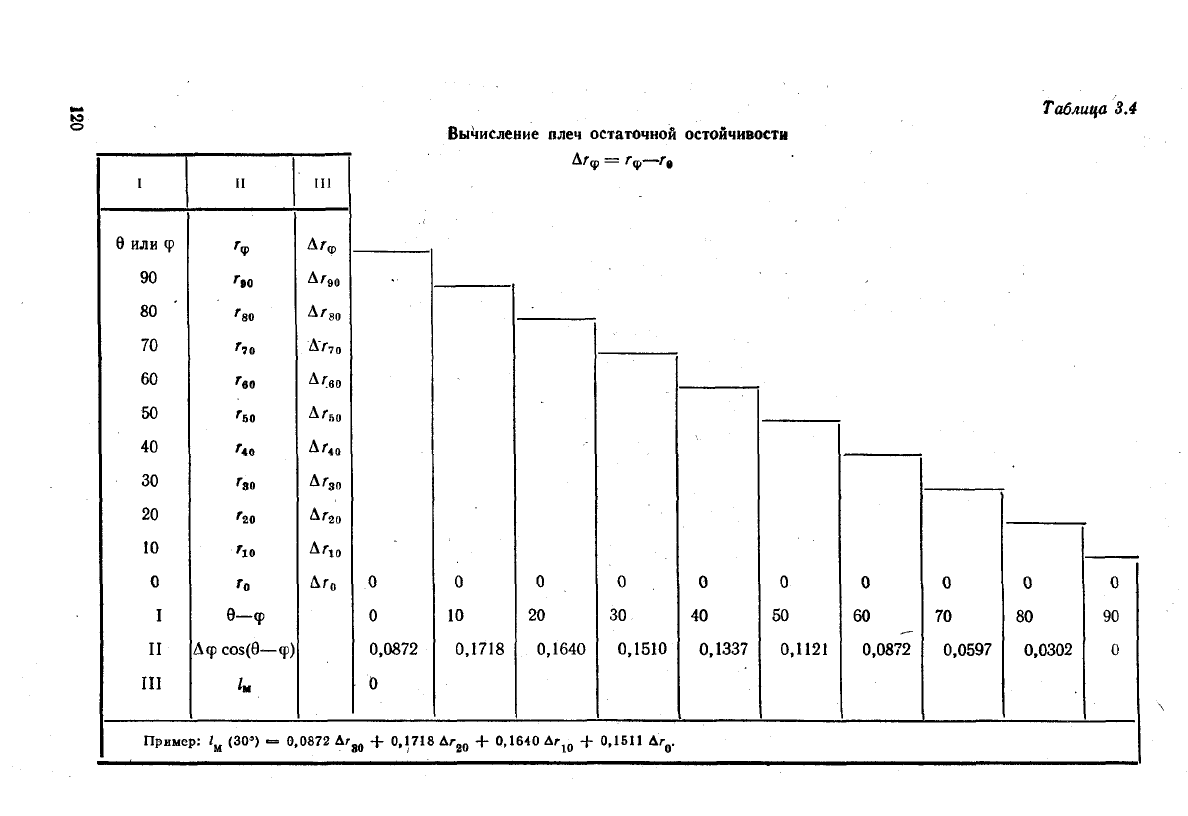
также в качестве плеча остойчивости формы принимать плечо остаточной
остойчивости, представляющее длину /
м
перпендикуляра, который опущен из мета-
центра т, соответствующего прямому положению судна на направление линии дей-
ствия силы поддержания,
/
м
=/
ф
_
Го
sin 9
(3.12)
или
в
'м
= [
(/-ф
— г
0
) cos (9 —
<р)
dtp.
(3.13)
Плечи
/
м
могут
быть положительными и отрицательными.
Плечо статической остойчивости в этом
случае
определяется формулой
1= l
u
+
hsinQ.
(3.14)
Производная
/
и
по
водоизмещению равна
ri/
M
^
1_
, _. ~ .
0 5
dV
V
где х
0
— дифференциальный метацентрический радиус в прямом положении судна
(§
26).
Плечо динамической остойчивости определяется общим выражением
'Sin6 —
zcosO
— о(1— cos8).
(3.16)
Геометрически плечо динамической остойчивости равно приращению вертикаль-
ного расстояния
между
центром тяжести и центром величины. На рис. 3.3 оно равно
отрезку
112

Из
формулы
(3.16)
следует,
что кривая динамической остойчивости является ин-
тегральной кривой по отношению к диаграмме статической остойчивости.
Из
приводимых здесь общих зависимостей вытекают следующие геометрические
свойства диаграмм статической остойчивости и динамической остойчивости, могущие
служить для контроля правильности вычислений.
1. Диаграмма статической остойчивости является нечетной функцией
угла
9,
а диаграмма динамической остойчивости — четной.
2. Если при значении 6 = 1 рад отложить ординату, равную начальной мета-
центрической высоте, и конец ее соединить прямой с началом координат, то получен-
ная
наклонная прямая должна быть касательной к диаграмме статической остойчи-
вости в начале координат.
3. Диаграмма динамической остойчивости должна касаться оси абсцисс в начале
координат, иметь точку перегиба при
угле
крена, соответствующем максимуму диа-
граммы статической остойчивости, и иметь максимум при крене, равном
углу
заката
диаграммы статической остойчивости.
При
больших
углах
крена судна центр величины его перемещается также и
в
продольном направлении, что создает дополнительный дифферентующий момент,
называемый
деривационным.
Благодаря этому поперечные наклонения судна должны
в
какой-то мере сопровождаться наклонениями его в продольной плоскости. Обычно
в
большинстве проектных расчетов влияние деривационных моментов не учитывается
и
рассматриваются только наклонения и восстанавливающие моменты в поперечной
плоскости. Расчеты, связанные с
учетом
деривационных моментов, т. е. с примене-
нием
методов теории пространственной остойчивости, приводятся в § 60 и 65.
§ 36.
РАСЧЕТ
ОСТОЙЧИВОСТИ НА БОЛЬШИХ
УГЛАХ КРЕНА ПО МЕТОДАМ А. Н. КРЫЛОВА
Общий порядок расчета остойчивости на больших
углах
крена по методам
А. Н. Крылова сводится к
следующему.
1. На чертеже корпуса проводится ряд равнообъемных ватерлиний при значе-
ниях
угла
крена 0, 10, 20, 30
е
и т. д.*
2. Вычисляются моменты инерции /
ф
площадей равнообъемных ватерлиний отно-
сительно продольной оси, проходящей через их центры тяжести.
3. Вычисляются метацентрические радиусы для каждого наклонения г
0
, г
10
, г
м
и
т. д. по формуле (3.2)
г -
г
<р
-
7
»
4. Пользуясь правилом трапеций, вычисляют значения координат центра вели-
чины
по формулам (3.1)
в
в
I» f
sin ф dq>.
у = /-ф созфйф; г =
5. Определяют плечи остойчивости формы /ф или ординаты диаграммы статиче-
ской
остойчивости по формулам (3.3) и (3.4)
/ф
= у cos в + z sin в;
/ = /ф — a sin в.
6. Операции 4 и 5
могут
быть заменены графическим построением полярной диа-
граммы остойчивости, описание которой дается ниже.
Для выполнения расчетов остойчивости на больших
углах
крена может служить
чертеж корпуса с нанесенными на нем теоретическими шпангоутами. Теоретические
шпангоуты должны быть двусторонними с построением как правой, так и левой ветви
* Равнообъемные ватерлинии проводятся иногда через 10
е
, а иногда и через 5"
в
вависимости от формы обводов судна и требуемой точности расчетов.
ИЗ
шпангоута, а также линия бимсов. Количество теоретических шпангоутов
прини-
мается от 11 до 21-го в зависимости от типа судна, характера обводов и требуемой
точности.
Маештаб корпуса выбирается таким, чтобы половина ширины судна измерялась
отрезком длиной не менее 150 мм.
Первый
способ А. Н. Крылова. Первый способ А. Н. Крылова
дает
наиболее
точные результаты в тех
случаях,
когда объем надводной части корпуса не очень
сильно
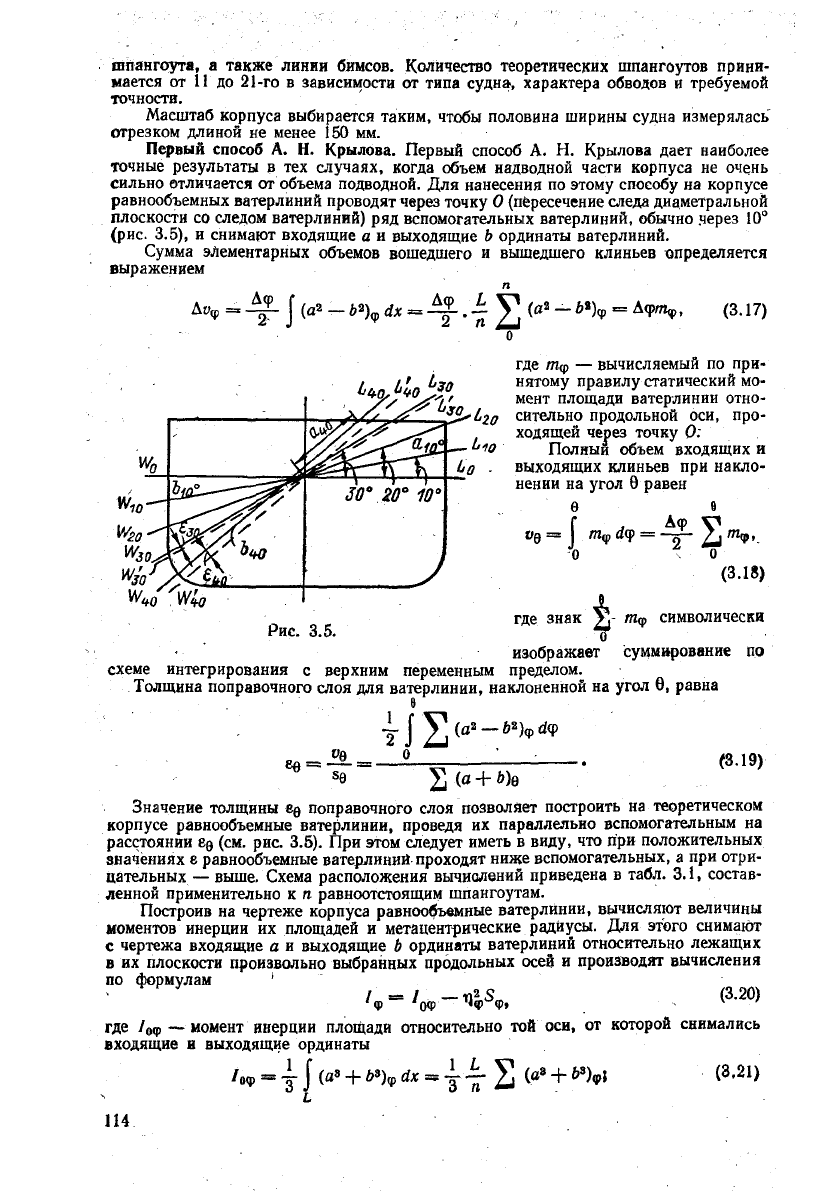
отличается от объема подводной. Для нанесения по этому способу на корпусе
равнообъемных ватерлиний проводят через точку О (пересечение следа диаметральной
плоскости
со следом ватерлиний) ряд вспомогательных ватерлиний, обычно через 10°
(рис.
3.5), и снимают входящие а и выходящие Ь ординаты ватерлиний.
Сумма элементарных объемов вошедшего и вышедшего клиньев определяется
выражением
.-
>>
:
а
а
—
(3.17)
где Шф — вычисляемый по при-
нятому правилу статический мо-
мент площади ватерлинии отно-
сительно продольной оси, про-
ходящей через точку 0:
Полный
объем входящих и
выходящих клиньев при накло-
нении
на
угол
6 равен
в
в
Г
, Аф
00=
т
Ф
аф = -_-
где
знак
)
Рис.
3.5. \
изображает
схеме
интегрирования с верхним переменным пределом.
Толщина
поправочного слоя для ватерлинии, наклоненной на
угол
в, равна
(3.18)
-
т
ф
символически
суммирование по
(3.19)
Значение
толщины ее поправочного слоя позволяет построить на теоретическом
корпусе равнообъемные ватерлинии, проведя их параллельно вспомогательным на
расстоянии
8д (см. рис. 3.5). При этом
следует
иметь в
виду,
что при положительных
значениях
г равнообъемные ватерлиний проходят ниже вспомогательных, а при отри-
цательных — выше. Схема расположения вычислений приведена в табл. 3.1, состав-
ленной
применительно к п равноотстоящим шпангоутам.
Построив
на чертеже корпуса равнообъемные ватерлинии, вычисляют величины
моментов инерции их площадей и метацентрические радиусы. Для этого снимают
с
чертежа входящие а и выходящие b ординаты ватерлиний относительно лежащих
в
их плоскости произвольно выбранных продольных осей и производят вычисления
по
формулам '
'V'Л
(3
-
20)
где /
оф
— момент инерции площади относительно той оси, от которой снимались
входящие в выходящие ординаты
4
т 2
С<*
8
+*
З
)Ф»
(3
-
21)
i
114
'Оф
:
4|(«
8
+
dx

—
площадь наклоненной под
углом
<р равнообъемной ватерлинии
)Ф;
(3.22)
т)
ф
— расстояние центра тяжести площади ватерлинии от оси, принятой при
съемке ординат [см. формулу
(3.23)
].
Метацентрический
радиус
для наклонной ватерлинии
'*
= —/
Ось отсчета ординат
следует
на глаз выбирать таким образом, чтобы величина tjq,
оказалась, по возможности, меньшей. Практическая
схема
расположения вычисле-
ний
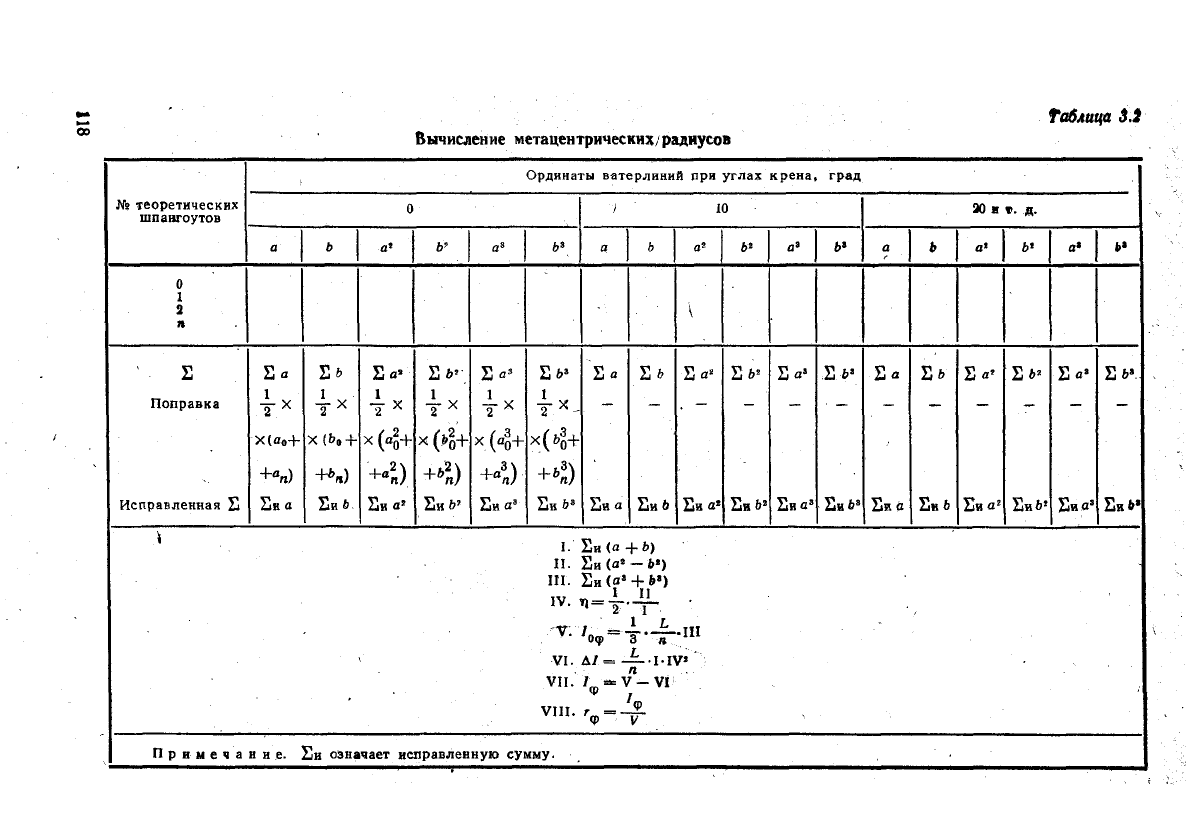
приведена в табл. 3.2.
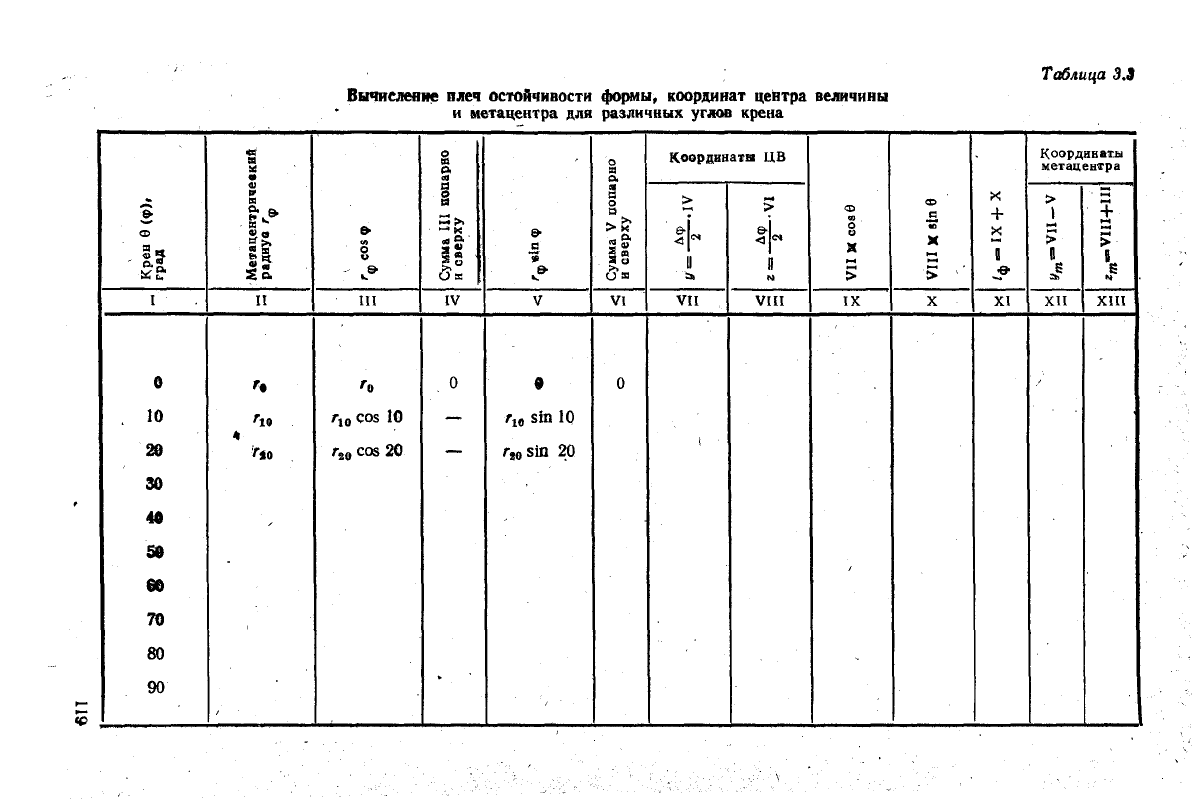
Вычисление плеч остойчивости формы и координат центра величины и метацентра
производится по формулам (3.1), (3.4) и (3.7)
в
ff = Г
/-ф
cos ф dy; &= Г г
ф
sin f
dq>;
/ф
= у cos в + z sin в;
Ут = У — 'е si"
е
; г
т
= z + г
в
cos 9.
Схема вычислений приведена в табл. 3.3.
Если
надводный объем мало отличается от подводного, что имеет место у высоко-
бортных
судов,
можно пренебречь толщиной поправочного слоя и считать пересекаю-
щиеся
в общей точке О вспомогательные ватерлинии совпадающими с равнообъем-
ными.
В этом
случае
возможно упростить расчет, отказавшись от вычислений, ука-
занных
в табл. 3.1, и сразу приступить к вычислениям табл. 3.2 и 3.3. Прием этот
также указан акад. А. Н. Крыловым. ^
В тех
случаях,
когда объем надводной части корпуса сильно отличается от под-
водного, суммарный объем входящих и выходящих клиньев, вычисляемый по фор-
муле
(3.18),
достигает
большой величины и определение толщины е поправочного слоя
по
формуле
(3.19)
становится неточным. В этих
случаях
для построения равнообъем-
ных ватерлиний
следует
применять второй способ акад. А. Н. Крылова, получивший
в
отечественной практике наибольшее распространение.
Второй способ А. Н. Крылова. По второму- способу расчета вспомогательные
ватерлинии проводят не через одну точку О, а последовательно каждый раз через
центр
тяжести равнообъемной ватерлинии.
Первую вспомогательную ватерлинию проводят под
углом
Д6 к начальной ватер-
линии
через ее центр тяжести, т. е. через точку О. После этого снимают входящие и
выходящие ординаты вспомогательной ватерлинии относительно точки О и вычисляют
расстояние
г\
центра тяжести наклонной ватерлинии от оси О по формуле
L
(а*-Ь*)
dx
А6
1
£(*»-*%,
'
( }
Толщина
поправочного слоя равна
4%-
(3.24)
Вычислив толщину поправочного слоя, проводят параллельно вспомогательной
равнообъемную ватерлинию на расстоянии е, причем если в > 0, то равнообъемная
ватерлиния
проходит ниже вспомогательной, а при е <« 0 — выше.
115

Вычисление толщин
№
теоретических шпангоутов
0
1
2
8
п
S
Поправка
н.
-2Й
<«•-»%
III.
Сумма II по два и слева
IV.
e-^L.ili
л
Ординаты ватерлиний
0
а
£(а
4f<
a
-
6
+
*)
f »).+
\-Ь)
п
]
а'
Ео>
£(а'
Г
ZJH \П -\- 0)о
Еи(а
2
-6
!
)о
0
-Ь')
10
а
£а
4[(
а
"
+
(а-
\
й
£*
f*)o +
£и(й
£и(а
г
1
О'
V 2
Е(а*
+
(°
г
-
+
6).»
Eft'
-ft»)
t
Примечание.
Ей означает исправленную
сумму.
Ввиду
малой толщины поправочного слоя считается, что центр тяжести /
х
равно-
объемной ватерлинии лежит на одной вертикали с центром тяжести вспомогательной,
Отсюда графически по известной т) находят на чертеже положение центра тяжести
равнообъемной ватерлинии.
Далее, через точку /, проводят новую вспомогательную ватерлинию, составляю-
щую
угол
2Д9 с начальной, снимают ее ординаты и определяют величины ц
2
и е
2
.
По
найденным значениям т)
2
и е
2
строят равнообъемную ватерлинию для наклонения
2Д9 и находят положение ее центра тяжести. Через точку f
2
проводят
следующую
вспомогательную ватерлинию, составляющую
угол
ЗД9 с начальной, и все операции
проводят в том же порядке.
Взамен вычисления толщин поправочного слоя по формуле
(3.24)
может быть
применено
графическое построение, предложенное Дарньи. Сущность построения
видна из рассмотрения рис. 3.6, где равнообъемные ватерлинии проведены сплош-
ными
линиями, а вспомогательные — пунктирными. Для построения равнообъемной
ватерлинии W
1
L
1
от точки О по начальной ватерлинии откладывается величина
OF,
=*=
1/2т)!,
и равнообъемная ватерлиния W
1
L
1
пройдет через точку F
v
Следующая
равнообъемная ватерлиния, соответствующая наклонению на 2Д8, пройдет через
точку F
2
> находящуюся на расстоянии
1/2т)
2
от точки f
v
Так
как толщины е поправочных слоев получаются достаточно малыми, можно
считать, что величины ординат равнообъемных ватерлиний не
"будут
заметно отли-
чаться от ординат вспомогательных ватерлиний. Поэтому вычисление моментов инер-
ции
площадей можно производить по ординатам, снятым для вспомогательных ватер-
линий.
Это сильно сокращает объем расчета. Схема производства вычислений полу-
чается вполне аналогичной той, которая применяется для расчета метацентрических
116
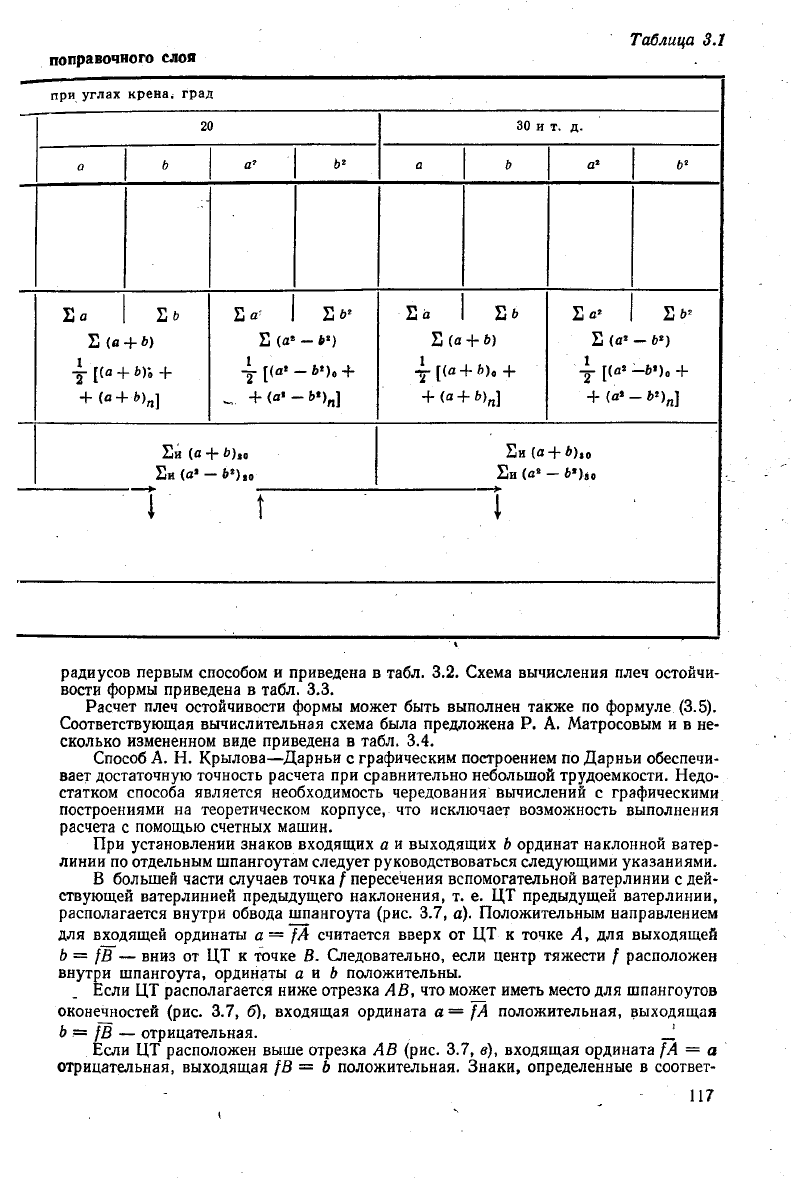
поправочного
слоя
Таблица
3.1
при
углах
крена, град
20
0
Еа
Е(а
+
(а 4
Ь
Efc
+
6)
-
*)i +
а'
Е(а'
1
г
_.
+(«'•
б
2
Ей
(а+ *>),„
Ей (а
1
-б*),.
30 и т. д.
а
Еа
Е(а
1
b
Еь
+
6)
Ей
(а
Ей
(а
8
if 1
а*
Ь'
Еь*
радиусов первым способом
и
приведена
в
табл.
3.2.
Схема вычисления плеч остойчи-
вости формы приведена
в
табл.
3.3.
Расчет плеч остойчивости формы может быть выполнен также
по
формуле (3.5).
Соответствующая вычислительная
схема
была предложена
Р. А.
Матросовым
и в не-
сколько измененном виде приведена
в
табл.
3.4.
Способ
А. Н.
Крылова—Дарньи
с
графическим построением по Дарньи обеспечи-
вает достаточную точность расчета
при
сравнительно небольшой трудоемкости. Недо-
статком способа является необходимость чередования вычислений
с
графическими
построениями
на
теоретическом корпусе,
что
исключает возможность выполнения
расчета
с
помощью счетных машин.
При
установлении знаков входящих
а и
выходящих
Ь
ординат наклонной ватер-
линии
по отдельным шпангоутам
следует
руководствоваться следующими указаниями.
В большей части
случаев
точка
/
пересечения вспомогательной ватерлинии
с
дей-
ствующей ватерлинией предыдущего наклонения,
т. е. ЦТ
предыдущей ватерлинии,
располагается внутри обвода шпангоута (рис.
3.7, а).
Положительным направлением
для входящей ординаты
a— fA
считается вверх
от ЦТ к
точке
А, для
выходящей
Ь
= \В —
вниз
от ЦТ к
точке
В.
Следовательно, если центр тяжести
/
расположен
внутри шпангоута, ординаты
а и ft
положительны.
Если
ЦТ
располагается ниже отрезка
АВ, что
может иметь место
для
шпангоутов
оконечностей
(рис. 3.7, б),
входящая ордината
а = fA
положительная, выходящая
b
= fB —
отрицательная.
_|
Если
ЦТ
расположен выше отрезка
АВ
(рис.
3.7, в),
входящая ордината
fA = a
отрицательная, выходящая
fB = Ь
положительная.
Знаки,
определенные
в
соответ-
117
Вычисление
метацентрических/радиусов
Таблица
S.S
№
теоретических
шпангоутов
0
1
2
ft
' £
Поправка
Исправленная £
\
П р и м е ч а
Ординаты ватерлиний при
углах
крена,
град
0
а
Еа
4-х
Х(а„+
Ей а
н
и е.
ft
Eft
4-х
Х(Ь.+
Еи»
•
а'
Еа»
1
х(4ь
Ей
а'
Ь'
ЕЙ'
Т
х
х(,
2
о+
Ей ft'
а
8
Еа»
Т
х
х(-о+
Ей а'
ft
3
Eft'
Т*-
х(Ьо+
Еиб»
I.
и.
ш.
IV.
V.
VI.
VII.
VIII.
Зи
означает исправленную
сумму.
)
' 10
а
Еа
Ей
а
Еи(а-
£и(а»
Ей
(а»
4=4"
Оф ~
д/=,
-
г
ф
=
-
ft
Eft
Ей»
a'
\
Еа«
Ей
а'
ft'
Eft'
Ей ft'
a'
Еа'
Ей а»
ft»
£ ft"
S
H
ft=
ao в т. д.
а
Еа
Еи
а
t-ft)
+
6»)
и
i
L.i.iv»
-VI
Г
Ф
V
ft
Eft
S
K
ft
а»
Еа'
Еиа*
ft'
£б
2
Ей*'
а»
£а-
Ей
а'
**
Eft'.
Ей
*•
Вычисление
плеч
остойчивости формы, координат центра величины
и
метацентра
для
различных
углов
крена
Таблица
3.3
CD
I
0
ю
20
30
40
5»
ее
70
80
90
В
м
и
•
я
ц-
«о
11
II
4
По
g
III
'в
г
10
cos
10
r
20
cos
20
арво
g
Сумма II
и
сверху
IV
0
_
—
©•
с
V
9
r
lt
sin 10
r
!e
sin 20
рно
о
а
Сумма
V
и
сверху
VI
0
Координата
UB
>
3»
VII
II
N
VIII
CD
VII
X
соа
IX
о
*5Г
X
X
X
«•
XI
Координаты
метацентра
|
I
5
XII
III+
|
XIII
Таблица
3.4
I
6
ИЛИ ф
90
80
70
60
50
40
30
20
10
0
I
II
III
II
Г
Ч>
r
t0
'so
'во
По
ы
Н
6—ф
Дф
cos(6—ф]
Ш
АА
Ф
д,
ад
Д/"80
А/-
70
AfAn
Д/'зо
Д'го
Д/-
о
Пример:
/
м
(30») — 0,0872 Ar
Вычисление
плеч
остаточной
АГф = /ф—^Г
в
0
0
0,0872
0
0
10
0,1718
0
20
0,1640
0
30
0,1510
g0
+ 0,1718
Лг
20
+ 0,1640 Дг
10
+ 0,1511 Д/у
остойчивости
0
40
0,1337
0
50
0,1121
0
60
0,0872
0
70
0,0597
0
80
0,0302
0
90
0
