Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


5A.6
Vector and Tensor Algebra in Curvilinear Coordinates
827
Y
Fig.
A.6-2.
Unit vectors in rectangular and
cylindrical coordinates. The z-axis and the unit
6~
vector 6, have been omitted for simplicity.
6,
/
/
/
/
/
H
P(x,
y,
Z)
or
P(Y,
0,
Z)
/
/
/
/
/
/
-/\"
X
With these relations, derivatives of any scalar functions (including, of course, compo-
nents of vectors and tensors) with respect to
x,
y,
and
z
can be expressed in terms of de-
rivatives with respect to r, 0, and
z.
Having discussed the interrelationship of the coordinates and derivatives in the two
coordinate systems, we now turn to the relation between the unit vectors. We begin
by
noting that the unit vectors ti,, 6,, 6, (or 6,, 6,, 6, as we have been calling them) are inde-
pendent of position-that is, independent of
x,
y,
z.
In cylindrical coordinates the unit
vectors 6, and 6, will depend on position, as we can see in Fig. A.6-2. The unit vector 6, is
a vector of unit length in the direction of increasing r; the unit vector 6, is a vector of unit
length in the direction of increasing
8.
Clearly as the point
P
is moved around on the
xy-
plane, the directions of 6, and 6, change. Elementary trigonometrical arguments lead
to
the following relations:
6,
=
(
cos 0)S,
+
(
sin O)Sy
+
(OM,
6,
=
(-
sin 0)6,
+
(cos 0)6,
+
(016,
6,
=
(016,
+
(016,
+
(116,
These may be solved for 6,, S,, and 6, to give
The utility of these two sets of relations will be made clear in the next section.
Vectors and tensors can be decomposed into components with respect to cylindrical
coordinates as was done for Cartesian coordinates in Eqs. A.2-16 and A.3-7 (i.e.,
v
=
6,v,
+
6,v,
+
6,~~). Also, the multiplication rules for the unit vectors and unit dyads are the
same as in
Eqs.
A.2-14 and 15 and A.3-1 to 6. Consequently the various dot and cross
product operations (but
~ot
the differential operations!) are performed as described in
55A.2 and
3.
For example,
+
etc.

828
Appendix
A
Vector and Tensor Notation
Spherical Coordinates
We now tabulate for reference the same kind of information for spherical coordinates r,
0,4. These coordinates are shown in Figure A.6-lb. They are related to the Cartesian co-
ordinates by
x
=
r sin 8 cos
4
(A.6-19)
r
=
+Ux2
+
y2
+
z2
(A.6-22)
y
=
r
sin 0 sin
4
(A.6-20) 0
=
arctan(m/z) (A.6-23)
z
=
r
cos 8 (A.6-21)
+
=
arctan(y/x) (A.6-24)
For the spherical coordinates we have the following relations for the derivative
operators:
COS
8
cos
4
=
(sin 0 cos
4)
dr
(A.6-25)
sin 0
d
d
(c0s8)++
(i)z
+
(01%
dr
The relations between the unit vectors are
6,
=
(sin 0 cos +)ti,
+
(sin 0 sin
+)ijy
+
(
cos
8%
(A.6- 28)
6,
=
(COS
8 cos 4)6,
+
(cos 0 sin 4)6y
+
(-
sin @6,
(A.6-29)
6,
=
(-
sin 4)6,
+
(
cos
4)GY
+
(OPz
(A.6-30)
and
6,
=
(sin 8 cos 4)6,
+
(cos 8 cos $)So
+
(-
sin 4)6+
(A.6-31)
Sy
=
(sin 8 sin
+)fir
+
(
cos
0
sin 4)S,
+
(
cos
(A.6-32)
6,
=
(cos 8)Fr
+
(-
sin 0)60
+
(ON+
(A.6-33)
And, finally, some sample operations in spherical coordinates are
That
is,
the relations (not involving
V!)
given in ssA.2 and
3
can be written directly
in
terms of spherical components.
EXERCISES
1.
Show that
lozT
j:
6, sin
B
do
=
o
lozT
j:
s,s,
sin
0 d~
d4
=
ti
where
6,
is the unit vector in the
r
direction in spherical coordinates.
2.
Verify that in spherical coordinates 6
=
63,
+
6,6,
+
6+6+.

5A.7 Differential Operations in Curvilinear Coordinates
829
5A.7 DIFFERENTIAL OPERATIONS
IN CURVILINEAR COORDINATES
We now
turn
to the use of the V-operator in curvilinear coordinates. As in the previous sec-
tion, we work out in detail the results for cylindrical and spherical coordinates. Then we sum-
marize the procedure for getting the V-operations for any orthogonal curvilinear coordinates.
Cylindrical Coordinates
From Eqs. A.6-10,11, and 12 we can obtain expressions for the spatial derivatives of the
unit vectors 6,, 6,, and 6,:
(A. 7-2)
The reader would do well to interpret these derivatives geometrically by considering the
way 6,, 6,, 6, change as the location of
P
is changed in Fig. A.6-2.
We now use the definition of the V-operator in Eq. A.4-1, the expressions in Eqs. A.6-
13, 14, and 15, and the derivative operators in Eqs. A.6-7,8, and 9 to obtain the formula
for
V
in cylindrical coordinates
d
sin
0
d
=
(6, cos
0
-
S,
sin 0)
d
+
(6, sin
0
+
6, cos 0)
When this is multiplied out, there is considerable simplification, and we get
for
cylindrical
coordinates. This may be used for obtaining all differential operations
in
cylin-
drical coordinates, provided that Eqs. A.7-1,2, and 3 are used to differentiate any unit vectors
on which
V
operates. This point will be made clear in the subsequent illustrative example.
Spherical Coordinates
The spatial derivatives of 6, 6,, and
6,
are obtained
by
differentiating Eqs. A.6-28/29, and 30:
d
d
d
-
6,
=
6, sin
0
-
6,
=
6+ cos 0
-
6+
=
-6, sin
0
-
S,
cos
8
d9 d+
(A.7-8)

830
Appendix A Vector and Tensor Notation
Use of Eqs. A.6-31,32, and
33
and Eqs. A.6-25,26, and 27 in Eq. A.4-1 gives the following
expression for the V-operator:
in
spherical
coordinates. This expression may be used for obtaining differential opera-
tions in spherical coordinates, provided that Eqs. A.7-6,7, and
8
are used for differentiat-
ing the unit vectors.
General Orthogonal Coordinates
Thus far we have discussed the two most-used curvilinear coordinate systems. We now
present without proof the relations for any orthogonal curvilinear coordinates. Let the
relation between Cartesian coordinates
xi
and the curvilinear coordinates
q,
be given by
These can be solved for the
q,
to get the inverse relations
q,
=
q,(xi).
~henl the unit vec-
tors
in rectangular coordinates and the
6,
in curvilinear coordinates are related thus:
in which the "scale factors"
h,
are given by
The spatial derivatives of the unit vectors
6,
can then be found to be
d6,
-
6p dhp
3
Gr
dh,
&p
E
--
ha
a%
y=1
hr
dqr
I
I
and the V-operator is
I
I
The reader should verify that Eqs. A.7-14 and 15 can be used to get Eqs. A.7-1 to
3,
A.7-5
and A.7-6
to
9.
From Eqs. A.7-15 and
14
we can now get the following expressions for the simplest
of the V-operations:
P.
Morse and
H.
Feshbach,
Methods
of
Theoretical Physics,
McGraw-Hill,
New
York
(1953),
p.
26
and
p.
115.

5A.7 Differential Operations in Curvilinear Coordinates
831
EXAMPLE
A.7-1
Differential Operations
in Cylindrical
Coordinates
In the last expression, the unit vectors are those belonging to the curvilinear coordinate
system. Additional operations may be found in Morse and Feshbach.'
The scale factors introduced above also arise in the expressions for the volume and
surface elements
dV
=
h,h,h,dqldq2dq,
and
dSap
=
hohpdqadqp(a
#
P);
here
dSap
is a surface
element on a surface of constant
y,
where
y
Z
a
and
y
#
p.
The reader should verify that
the volume elements and various surface elements in cylindrical and spherical coordi-
nates can be found in this way.
In Tables A.7-1,2, and
3
we summarize the differential operations most commonly en-
countered in Cartesian, cylindrical, and spherical coordinates.* The curvilinear coordinate
expressions given can be obtained by the method illustrated in the following two examples.
Derive expressions for
(V
v)
and
Vv
in cylindrical coordinates.
SOLUTION
(a)
We begin
by
writing
V
in cylindrical coordinates and decomposing
v
into its components
Expanding, we get
We now use the relations given in Eqs. A.7-1,2, and
3
to evaluate the derivatives of the unit
vectors. This gives
Since
(6,
6,)
=
1,
(6,.
6,)
=
0,
and so on, the latter simplifies to
which is the same as
Eq.
A
of Table A.7-2. The procedure is
a
forward.
(A.
7-22)
bit tedious, but is
is
straight-
'
For other coordinate systems see the extensive compilation of
P.
Moon and D.
E.
Spencer,
Field
Theory
Handbook,
Springer, Berlin (1961). In addition, an orthogonal coordinate system is available in
which one of the three sets of coordinate surfaces is made up of coaxial cones (but with noncoincident
apexes); all of the V-operations have been tabulated by the originators of this coordinate system,
J.
F.
Dijksman and
E.
P.
W.
Savenije,
Rheol.
Acta,
24,105-118
(1985).

832
Appendix
A
Vector and Tensor Notation
Table
A.7-1
Summary of Differential Operations Involving
the
V-Operator in Cartesian
Coordinates
(x,
y,
z)
dux dv, dv,
(V.v)=-+-+-
dx dy dz
d2s d2s d2s
(V2s)
=
-
+
-
+
-
dx2 dy2 dz2
+
7
vx
(3)
ax
+
'YY
("y)
+
y2
(3)
ds
[Vs],
=
-
dx
as
[Vs],
=
-
dY
ds
[Vs],
=
-
dz
dv,
JVy
[V
x
v],
=
-
-
-
dy dz
dux dvz
[V
x
v]"
=
-
-
-
-
dZ dx
dvy dv,
[V
x
v],
=
-
-
-
dx dy
d7,,
J7,,
a~,,
[V.T],=-+--+-
dx dy dz
d7xy d7yy d7Zy
[V.T]
=-+--+-
Y
dx dy dz
d7,, d7y2 d7,,
[V.7],=-+-+-
dx dy dz
a2vX d2v, d2vX
[V2v],
=
-
+
-
+
-
dx2
dy2 dz2
d2vy d2vy d2vy
[V2v]
=
-
+
-
+
-
bx2 dy2 dz2
d2vZ d2v, d2v,
[V2v],
=
---
+
-
+
-
dx2 dy2 dz2
[v
Vw],
=
v,($)
+
vy(%)
+
%(%)
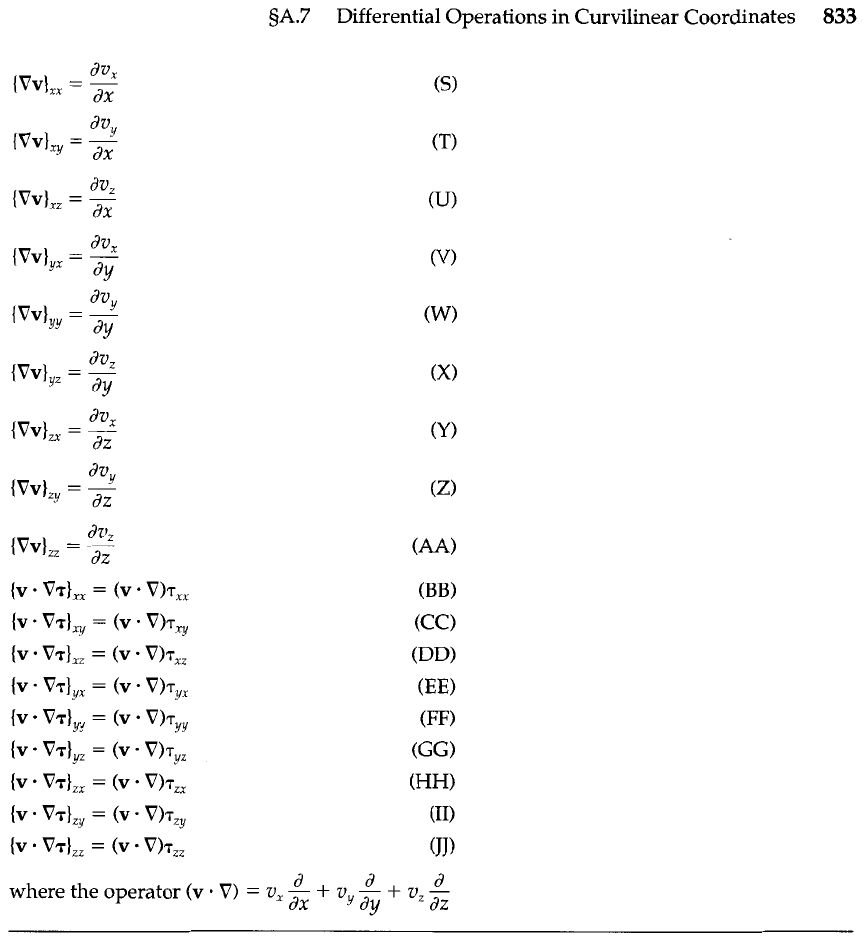
sA.7
Differential Operations in Curvilinear Coordinates
833
d d d
where the operator
(v
.
V)
=
v,
-
+
v
-
+
v,
-
dx
Y
dy dz

834
Appendix
A
Vector and Tensor Notation
Table
A.7-2
Summary of Differential Operations Involving the V-Operator in Cylindrical
Coordinates
(r, 6, z)
1
d
1
(9% dvz
(V-v)
=
--(rv,)
+
--
+
-
r dr r
do
dz
1
dv,
(T:VV)
=
rrr($)
+
rr,(rdB
-
4)
+
rr2(2)
+
Tor(z)
+
roe(+
3
+
:)
+
roZ(g)
ds
[Vs],
=
-
dr
1
ds
[Vs],
=
-
-
r
do
ds
[Vs],
=
-
dz
1
dvz dv,
[V
Xv],=----
r
do
dz
dv, dv,
[Vxvl
--dy
*-
dz
1
d
1
Jv,
[V
x
v],
=
--(rue)
-
--
r dr r a0
1
d
1
d
d
Too
[V
'
71,
=
-
-
(rr,,)
+
-
-
Tor
+
-
rzr
-
-
r dr
r
do
dz r
1
d
1
d
d
7er
-
7re
[V
'
'TIe
=
-
-
+
-
-
Tee
+
-
Tze
+
p
?
dr
r
de
dz
r
1
d
1
d
d
[V
.
71,
=
-
-
(rr,)
+
-
-
roz
+
-
r,,
r dr r a0 dz
[vbl,
=~i~(~z)
+
L&+%
r dr r2
do2
dz2
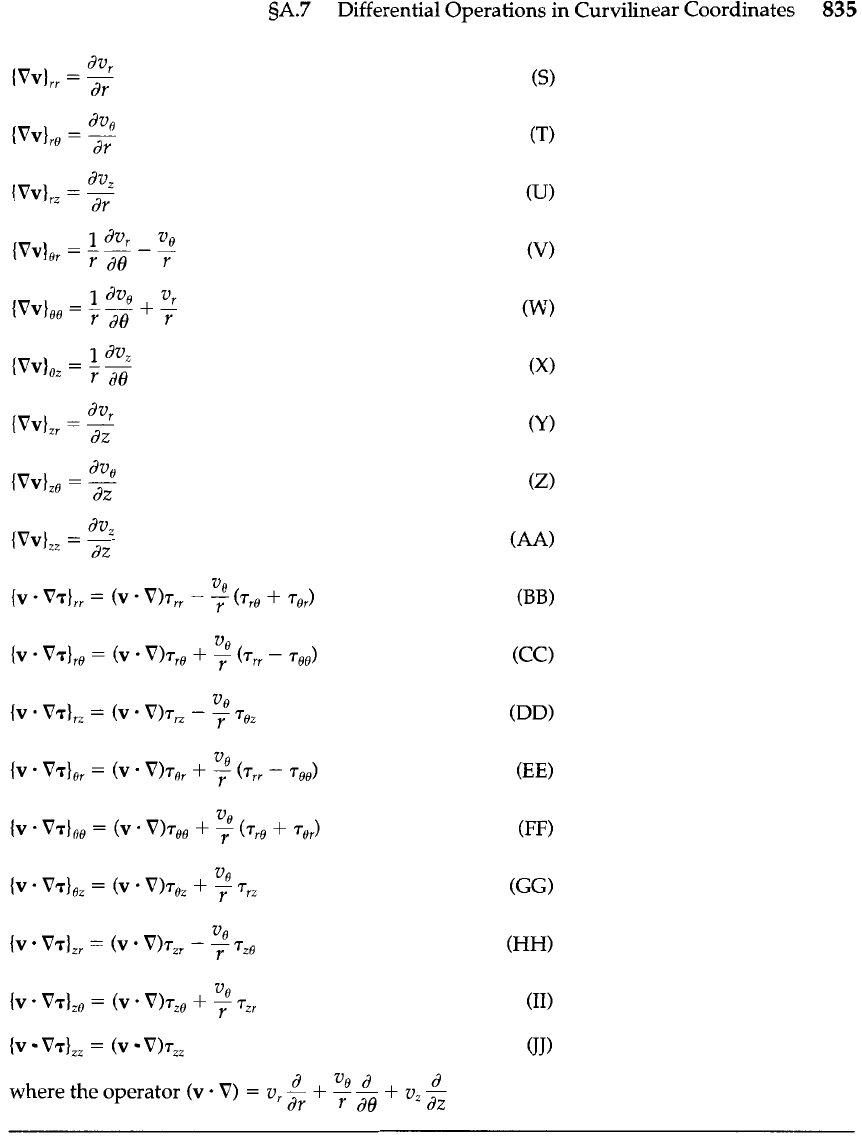
gA.7
Differential Operations in Curvilinear Coordinates
835
V@
(v
'
V7),"
=
(v
'
V)r,,
+
y
T,,
(11)
(v
VT),,
=
(v
v)T,,
(JJ)
d
v,
d
d
where the operator
(v
.
V)
=
v,
-
+
-
-
+
v,
-
dr
r
a6 az
836
Appendix
A
Vector and Tensor Notation
Table
A.7-3
Summary of Differential Operations Involving the V-Operator
in
Spherical Coordinates (r, 8,4)
ds
[Vsl,
=
-
dr
1
ds
[Vsl,
=
-
-
d8
1
ds
[VsI+
=
v
-
r sin 8
d4
1
d
[V xvl,=--
1
dvO
(v, sin 8)
-
-
r sin 0
dd
r sin 8
d4
1
dvr
1
d
[V
xv],
=----(rv&
r sin 8
d+
r dr
1
il
1
dv,
[V
x
vl,
=
--
(rv,)
-
--
r dr r d8
1
d
1
d
1
d
708
+
74,
[V
-
I],
=
-
-
(?rJ
+
v
-
(rBr sin 8)
+
------
-
r2
dr r sin 8
dB
r sin 8
d+
r+r
-
Y
1
d
1
d
1
d
(rer
-
rr0)
-
744
cot 0
[V
-11,
=
-
-
(r3rr,)
+
--
-
(roo sin 8)
+
-
-
r3
dr r sin 0 d6 r sin 8
a4
"'
+
r
Id
3
1
d
1
d
(T,,
-
rr4)
+
rdo cot 8
[V
.
714
=
3
-
(r rr+)
+
v
-
(r,+ sin 8)
+
------
-
r dr
r sin 8 d8
r sin 8
d+
r4'
+
r
1
r2vr)
+
-
-
1 d2v,
2
(7
2
dv+
,V2vlr
=
-
(-
-
(
)
(sin8%)++sin2(jd+2
?sined*
(v, sin 8)
-
-
--
dr
r2
dr r2 sin 8
do
?
sin 8
d4
(v,
sin 8)
+
1
#vB
I
2
dvr
2
cot
e
)
$sin'~d+~ r2d8 r2sin8d6
(v, sin 8)
+
1 d2v,
+--+----
2
dvr
2
cot 8 due
)
?sin28d4' r2sin8d6 r2sin0d$
1
dw
1
dw,
W,
[V
'
=
+
v,(T
%
-
:)
+
v4(=%
-
?)
[V
.
,w,,
=
,.(?)
+
,,(;
2
+
?)
+
2
-
8)
1 dw* w
w,
+I+,
cot 8
[V
VWI+
=
vr(2)
+
v,(+
2)
+
v4(-
r
