Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.

5A.7
Differential Operations in Curvilinear Coordinates
837
1
duo
7'4
-
cot 8
{V~i+o
=
-
r
1
dv+
vr
v,
{VV},,,,~
=
-
-
+y+y~0t8
r sin 8
d+
d
Ve
d
+
d
where the operator
(v
V)
=
vr
-
+
--
+
-
-
dr r d8 r sin 0
d+

838
Appendix A Vector and Tensor Notation
(b)
Next we examine the dyadic product
Vv:
Hence, the rr-component is dvr/dr, the re-component is dv,/dr, and so on, as given in Table
A.7-2.
Find the r-component of
[V
.
T]
in spherical coordinates.
Differential Operations SOLUTION
in Spherical
Coordinates
Using Eq. A.7-9 we have
[o
.
TI,
=
[{6,
$
+
6,
{g&~~,
+
wo~ro
+
8,6+7,+
+
606r7e,
+
6&371j8
+
6&+70+
f
6+6r7+r
+
6$07,0
+
6+647++)
I
(A.7-24)
We now use Eqs. A.7-6, 7,
8
and
Eq.
A.3-3. Since we want only the r-component, we select
only those terms that contribute to the coefficient of
6,:
I
d
[6,
f
$
6,6rr,r]
=
16,
.
6,8,]
-
r
-
dB
nr
+
other term
(A.7-26)
+
other term
[a+
L
r sin 0
d+
.6&74,]
=
16,
-
6+6.l
a
(A.7-27)
[6,
i
$
.
6T6r7]
=
$
(6
{$
6,h]
+
[61 6. {$6r}]
1
6r6rrrr]
=
[S,
.
{&
6,}6,]
[a+
--
-
.
r sin 9
d+
r sin 0
-
7rr
--
7rr
[6, 64
sin
8
6,l
=
6,
r sin 0
[a,
$
.
6&&7,,]
=
6,.
~;g)
+
other term
Tor
COS
9
r
sin 9
1
d
[6+
d0
6+6,7++]
=
6,(~)
+
other terms

gA.8 Integral Operations in Curvilinear Coordinates
839
Combining the above results we get
Note that this expression is correct whether or not
T
is symmetric.
EXERCISES
1.
If
r
is the instantaneous position vector for a particle, show that the velocity and acceleration
of the particle are given by (use
Eq.
A.7-2):
in cylindrical coordinates. The dots indicate time derivatives of the coordinates.
2.
Obtain
(V
.
v), [V
X
v], and Vv in spherical coordinates, and [V
.
TI
in cylindrical coordinates.
3.
Use Table A.7-2 to write down directly the following quantities in cylindrical coordinates:
(a)
(V
.
pv), where
p
is a scalar
(b)
[V
.
pwl,,
where
p
is a scalar
(c)
[V
p6l0, where
p
is a scalar
(dl
(V
.
[T v])
(e)
[v. Vvl,
(f)
VV
+
(Vdt
4.
Venfy that the entries for V2v in Table A.7-2 can be obtained by any one of the following methods:
(a)
First verify that, in cylindrical coordinates the operator
(V
V)
is
and then apply the operator to
v.
(b)
Use the expression for [V
TI
in Table A.7-2, but substitute the components for Vv in place
of the components of
T,
SO
as to obtain [V
.
Vvl.
(c)
Use
Eq.
A.4-22:
and use the gradient, divergence, and curl operations in Table A.7-2 to evaluate the opera-
tions on the right side.
sA.8 INTEGRAL OPERATIONS
IN CURVILINEAR COORDINATES
In performing the integrations of sA.5 in curvilinear coordinates, it is important to un-
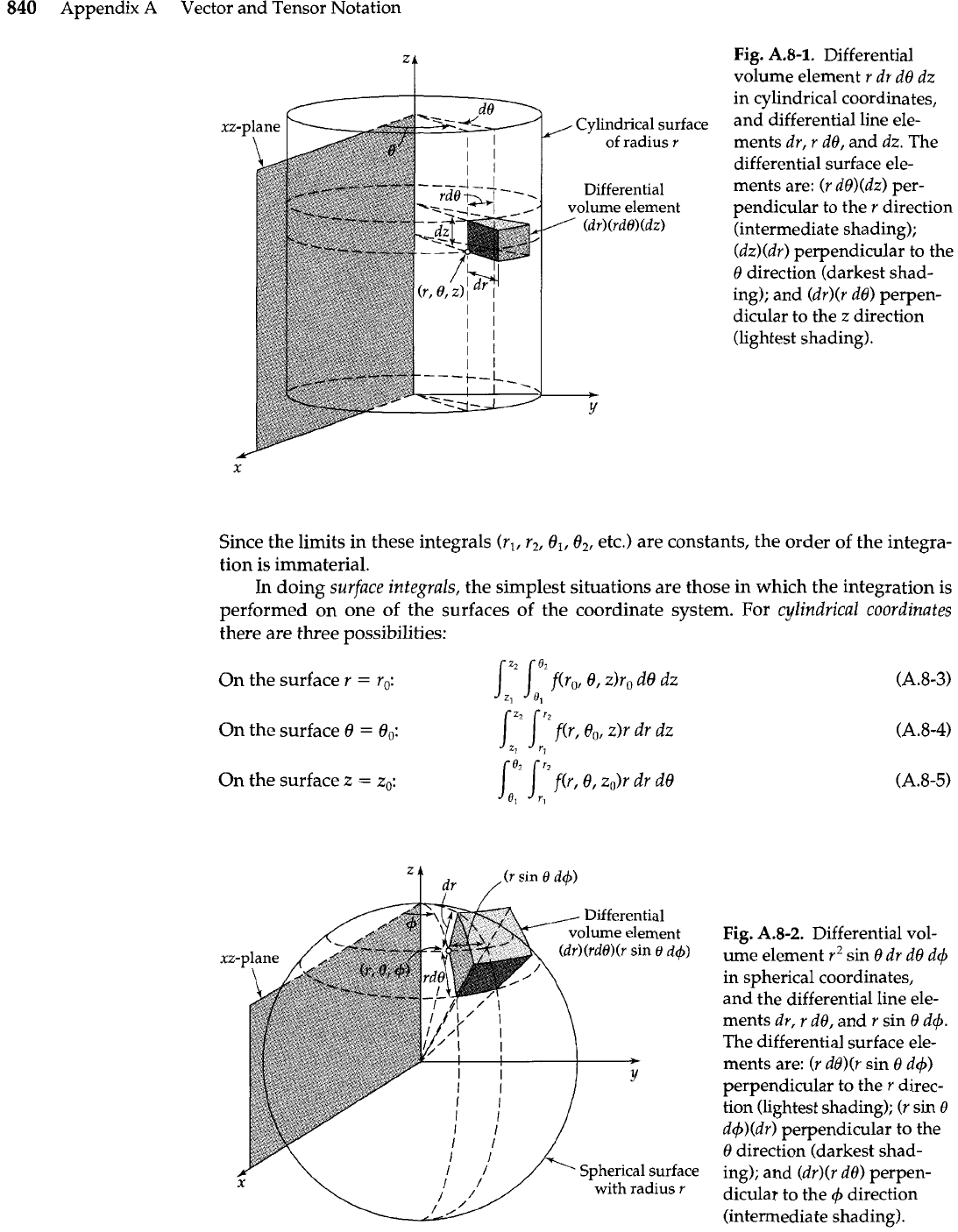
derstand the construction of the volume elements, as is shown for cylindrical coordi-
nates in Fig. A.8-1 and for spherical coordinates in Fig. A.8-2.
In doing volume integrals, the simplest situations are those in which the bounding
surfaces are surfaces of the coordinate system. For cylindrical coordinates, a typical vol-
ume integral of a function f(r, 0,
z)
would
be
of the form
and for spherical coordinates a typical volume integral of a function g(r, 0,
+)
would be
lo:
1,;
g(r,
0,
+)?
dr
sin 0 d0 d+
840
Appendix A Vector and Tensor Notation
Fig.
A.8-1.
Differential
volume element r dr dB dz
in cylindrical coordinates,
Cylindfical
surface
and differential line ele-
of radius
r
ments dr, r do, and dz. The
differential surface ele-
Differential
ments are: (r d0)(dz) per-
volume element
pendicular to the r direction
(dr)(rdO)(dz)
(intermediate shading);
(dz)(dr) perpendicular to the
8 direction (darkest shad-
ing); and (dr)(r de) perpen-
dicular to the z direction
(lightest shading).
Since the limits in these integrals (r,, r,, S,, S2, etc.) are constants, the order of the integra-
tion is immaterial.
In doing surface integrals, the simplest situations are those
in
which the integration is
performed on one of the surfaces of the coordinate system. For cylindrical coordinates
ihere are three possibilities:
On the surface r
=
r,:
On the surface
0
=
80:
On
the surface
z
=
2,:
/I
Spherical surface
X
with radius
r
Fig.
A.8-2.
Differential vol-
ume element r2 sin 8 dr d0 d+
in spherical coordinates,
and the differential line ele-
ments dr, r do, and r sin 8 d+.
The differential surface ele-
ments are: (r d8)(r sin 8 d+)
perpendicular to the r direc-
tion (lightest shading); (r sin 8
d+)(dr) perpendicular to the
0
direction (darkest shad-
ing); and (dr)(r do) perpen-
dicular to the
4
direction
(intermediate shading).

5A.9
Further Comments on Vector-Tensor Notation 841
Similarly, for
spherical coordinates:
On the surface
C$
=
&:
Ir:
g(r,
8,
C$&r2 dr
sin
B
do
The reader should try making sketches to show exactly what areas are described by each
of the above six surface integrals.
If the area of integration in a surface integral is not one of the surfaces of the coordi-
nate system, then a book on differential and integral calculus should be consulted.
sA.9 FURTHER COMMENTS ON VECTOR-TENSOR NOTATION
The boldface notation used in this book is called
Gibbs notation.'
Also widely used is an-
other notation referred to as Cartesian tensor n~tation.~ As shown in Table
A.9-1,
a few
examples suffice to compare the two systems. The two outer columns are just two differ-
ent ways of abbreviating the operations described explicitly in the middle column in
Cartesian coordinates. The rules for converting from one system to another are as
follows.
To convert
from
expanded notation to Cartesian tensor notation:
1.
Omit all summation signs (the "Einstein summation convention")
2.
Omit all unit vectors and unit dyads.
3.
Replace
d/dx,
by
di.
Table
A.9-1
Expanded notation in terms of
Gibbs
notation unit vectors and unit dyads Cartesian tensor notation
'
J.
W.
Gibbs,
Vector Analysis,
Dover
Reprint, New
York
(1960).
'
W.
Prager,
Mechanics of Continua,
Ginn,
Boston
(1961).

842
Appendix A Vector and Tensor Notation
To convert from Cartesian tensor notation to expanded notation:
1.
Supply summation signs for all repeated indices.
2.
Supply unit vectors and unit dyads for all nonrepeated indices; in each term of a
tensor equation the unit vectors must appear in the same order in the unit dyads.
3.
Replace
di
by
d/dxi.
The Gibbs notation is compact, easy to read, and devoid of any reference to a particular
coordinate system; however, one has to know the meaning of the dot and cross opera-
tions and the use of boldface symbols. The Cartesian tensor notation indicates the nature
of the operations explicitly in Cartesian coordinates, but errors in reading or writing sub-
scripts can be most aggravating. People who know both systems equally well prefer the
Gibbs notation for general discussions and for presenting results, but revert to Cartesian
tensor notation for doing proofs of identities.
Occasionally
matrix notation
is used to display the components of vectors and ten-
sors with respect to designated coordinate systems. For example, when
v,
=
jy,
vy
=
0,
v,
=
0,
Vv
can be written in two ways:
The second
"="
is not really an "equals" sign, but has to be interpreted as "may be dis-
played as." Note that this notation is somewhat dangerous since one has to infer the unit
dyads that are to be multiplied by the matrix element-in this case, 6,6,, tixsy, and so
on. If we had used cylindrical coordinates,
Vv
would be represented by the matrix
y
sin
8
cos
6
-
y
sin2
6
(A.9-2)
0
where the matrix elements are understood to be multiplied
by
6,6,
6,6e, and so on, and
then added together.
Despite the hazard of misinterpretation and the loose use of
"=,"
the matrix nota-
tion enjoys widespread use, the main reason being that the "dot" operations correspond
to standard matrix multiplication rules. For example,
Of course such matrix multiplications are meaningful only when the components are re-
ferred to the same unit vectors.

Appendix
B
The
Fluxes
and the Equations
of
Change
Newton's law of viscosity
Fourier's law of heat conduction
Fick's (first) law of binary diffusion
The equation of continuity
The equation of motion in terms of
T
The equation of motion for a Newtonian fluid with constant
p
and
p
The dissipation function
a,
for Newtonian fluids
The equation of energy in terms of
q
The equation of energy for pure Newtonian fluids with constant
p
and
k
The equation of continuity for species
a
in terms of
j,
The equation of continuity for species
A
in terms of
w,
for constant
p9,,
1
NEWTON'S LAW OF VISCOSITY
[T
=
-p(Vv
+
(VvIt)
+
(&u
-
K)(V. v)81
Cartesian coordinates
(x, y,
z):
in
which
(B.1-1)"
(B.
1
-2)"
(B.
1-3)"
(B.
1
-4)
(B.l-5)
(B.l-6)
(B.l-7)
"
When the fluid is assumed to have constant density, the term containing
(V
.
v)
may be omitted. For
monatomic gases at low density, the dilatational viscosity
K
is zero.
843

844
Appendix
B
Fluxes and the Equations
of
Change
1
NEWTON'S LAW OF VISCOSITY
(continued)
Cylindrical coordinates (r,
0,~):
in which
"
When the fluid is assumed to have constant density, the term containing
(V
.
v)
may be omitted. For
monatomic gases at low density, the dilatational viscosity
K
is zero.
Spherical coordinates (r, 0,4):
in which
+
($p
-
K)(V V)
(B.l-15)"
(B.l-16)"
vr
+
v,
cot
0
r
+
(ip
-
K)(V V)
(B.l-17)"
(B.1-18)
(B.1-19)
[
1
+
.
(")I
T+~
=
rr4
=
-p
v-
(B.l-20)
r
sm
6
d+
dr r
1
d
1
8%
(u,
sin
8)
+
----
-
(V mv)
=
--(r2vr)
+--
(B.1-21)
r2
dr
r
sin
8 d0 r
sin
8
d4
"
When the fluid is assumed to have constant density, the term containing
(V
-
v)
may be omitted. For
monatomic gases at low density, the dilatational viscosity
K
is zero.

sB.2
Fourier's
Law
of
Heat
Conduction
845
sB.2
FOURIER'S
LAW
OF
HEAT
CONDUCTIONa
[q
=
-kVTI
Cartesian coordinates
(x,
y, 2):
Cylindrical coordinates (r, 8,~):
Spherical coordinates (r, 8'4):
1
dT
q+
=
-k--
r sin
8
d4
a
For
mixtures,
the term
z,(E,/M,)~,
must be
added
to
q
(see
Eq.
19.3-3).

846
Appendix
B
Fluxes and the Equations
of
Change
5B.3
FICK'S (FIRST) LAW OF BINARY DIFFUSIONa
[jA
=
-P%ABVWAI
Cartesian coordinates (x,
y,
z):
Cylindrical coordinates tr,
8,~):
Spherical coordinates tr,
8,4):
"
To get the molar fluxes with respect to the molar average velocity, replace
j,,
p,
and
w,
by
J:,
c,
and
x,.
5B.4
THE EQUATION
OF
CONTINUITYa
[dp/dt
+
(V
.
pv)
=
01
Cartesian coordinates
(x,
y,
z):
Cylindrical coordinates (r,
8,~):
Spherical coordinates (r,
8,
4):
1
d
(pv,
sin
8)
+
-
-
(pv+)
=
0
3
+
--
(p?ur)
+
--
dt
y2
dr r
sin
8
d8
r
sin
8
dr$
"
When the fluid is assumed to have constant mass density
p,
the equation simplifies to
(V
.
v)
=
0.
