Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


Appendix
A
Vector and Tensor ~otation'
Vector operations from a geometrical viewpoint
Vector operations in terms of components
Tensor operations in terms
of
components
Vector and tensor differential operations
Vector and tensor integral theorems
Vector and tensor algebra in curvilinear coordinates
Differential operations in curvilinear coordinates
Integral operations in curvilinear coordinates
Further comments on vector-tensor notation
The physical quantities encountered in transport phenomena fall into three categories:
scalars, such as temperature, pressure, volume, and time; vectors, such as velocity, mo-
mentum, and force; and (second-order) tensors, such as the stress, momentum flux, and
velocity gradient tensors. We distinguish among these quantities by the following
notation:
s
=
scalar (lightface Italic)
v
=
vector (boldface Roman)
T
=
second-order tensor (boldface Greek)
In addition, boldface Greek symbols with one subscript (such as
i3J
are vectors.
For vectors and tensors, several different kinds of multiplication are possible. Some
of these require the use of special multiplication signs to be defined later: the single dot
(m),
the double dot
(:),
and the cross
(X).
We enclose these special multiplications, or sums
thereof, in different kinds of parentheses to indicate the type of result produced:
( )
=
scalar
[
1
=
vector
(
}
=
second-order tensor
No special significance is attached to the kind of parentheses if the only operations en-
closed are addition and subtraction, or a multiplication in which
.,
:,
and
x
do not ap-
pear. Hence (v
w)
and (.r:Vv) are scalars,
[V
x
v]
and
[I
v] are vectors, and {v
.
VT}
and
'
This appendix is very similar to Appendix
A
of
R.
B.
Bird,
R.
C.
Armstrong, and
0.
Hassager,
Dynamics of Polymeric Liquids, Vol.
I,
Fluid Mechanics,
2nd edition, Wiley-Interscience, New York
(1987).
There, in
98,
a discussion of nonorthogonal coordinates is given. Also
in
Table
A.7-4,
there is a summary
of
the
del operations for bipolar coordinates.

808
Appendix A Vector and Tensor Notation
{a
T
+
7
.
a}
are second-order tensors. On the other hand, v
-
w may be written as
(V
-
w),
[V
-
w], or
{V
-
w},
since no dot or cross operations appear. Similarly vw, (vw),
[vwl, and {vw) are all equivalent.
Actually, scalars can be regarded as zero-order tensors and vectors as first-order ten-
sors. The multiplication signs may be interpreted thus:
Multiplication Sign Order of Result
None
X
in which
C
represents the sum of the orders of the quantities being multiplied. For exam-
ple,
ST
is of the order 0
+
2
=
2,
vw
is of the order
1
+
1
=
2,6,6, is of the order
1
+
1
=
2,[vxwlisoftheorder1
+
1
-
1
=
l,(a:.r)isoftheorder2+2 -4=O,and(o.~}isof
the order 2
+
2
-
2
=
2.
The basic operations that can be performed on scalar quantities need not be elabo-
rated on here. However, the laws for the algebra of scalars may be used to illustrate
three terms that arise in the subsequent discussion of vector operations:
a.
For the multiplication of two scalars, r and s, the order of multiplication is imma-
terial so that the commutative law is valid: rs
=
sr.
b.
For the successive multiplication of three scalars,
q,
r,
and s, the order in which
the multiplications are performed is immaterial, so that the associative law is
valid: (qr)s
=
q(rs).
c.
For the multiplication of a scalar s by the sum of scalars
p,
q,
and r, it is immater-
ial whether the addition or multiplication is performed first, so that the distribu-
tive law is valid: s(p
+
q
+
r)
=
sp
+
sq
+
sr.
These laws are not generally valid for the analogous vector and tensor operations de-
scribed
in
the following paragraphs.
A VECTOR OPERATIONS FROM
A GEOMETRICAL VIEWPOINT
In elementary physics courses, one is introduced to vectors from a geometrical stand-
point. In this section we extend this approach to include the operations of vector multi-
plication. In 9A.2 we give a parallel analytic treatment.
Definition of a Vector and Its Magnitude
A
vector v is defined as a quantity of a given magnitude and direction. The magnitude of
the vector is designated by Ivl or simply by the corresponding lightface symbol
v.
Two
vectors
v
and w are equal when their magnitudes are equal and when they point in the
same direction; they do not have to be collinear or have the same point of origin. If v and
w have the same magnitude but point in opposite directions, then v
=
-w.
Addition and Subtraction of Vectors
The addition of two vectors can be accomplished by the familiar parallelogram construc-
tion, as indicated by Fig. A.l-la. Vector addition obeys the following laws:

A Vector Operations from a Geometrical Viewpoint
809
Commutative:
Associative:
Fig.
A.1-1.
(a)
Addition of vectors;
(b)
subtraction of vectors.
v
Vector subtraction is performed by reversing the sign of one vector and adding; thus
v
-
w
=
v
+
(-w). The geometrical construction for this is shown in Fig. A.1-lb.
Multiplication of a Vector
by
a Scalar
When a vector is multiplied by a scalar, the magnitude of the vector is altered but its di-
rection is not. The following laws are applicable
Commutative: sv
=
vs
(A.1-3)
Associative: r(sv)
=
(rs)v
(A. 1-4)
Distributive
(q
+
r
+
S)V
=
qv
+
rv
+
sv
(A.1-5)
Scalar Product (or Dot Product) of Two Vectors
The scalar product of two vectors
v
and w is a scalar quantity defined by
(v
w)
=
vw
cos
+,,
(A.1-6)
in which
+,
is the angle between the vectors
v
and
w.
The scalar product is then the
magnitude of
w
multiplied by the projection of
v
on w, or vice versa (Fig. A.1-2a). Note
that the scalar product of a vector with itself is just the square of the magnitude of the
vector
The rules governing scalar products are as follows:
Commutative:
Not Associative:
Distributive:
The length
of this
vector
equals
w
,4,
Area
(v
.
w)
(A.1-7)
(A.
1-8)
(A.
1-9)
(A.1-10)
Fig.
A.1-2.
Products of two vectors:
(a)
the scalar product;
(b)
the vec-
tor product.

810
Appendix A Vector and Tensor Notation
Vector Product (or Cross Product) of Two Vectors
The vector product of two vectors
v
and
w
is a vector defined by
[V
X
WI
=
IVW
sin
+,,In,,
(A.1-11)
in which n,, is a vector of unit length (a "unit vector") perpendicular to both
v
and
w
and pointing in the direction that a right-handed screw will move if turned from
v
to-
ward
w
through the angle
+,,.
The vector product is illustrated in Fig. A.l-2b. The mag-
nitude of the vector product is just the area of the parallelogram defined by the vectors
v
and
w.
It follows from the definition of the vector product that
Note the following summary of laws governing the vector product operation:
Not
Commutative:
[v
X
w]
=
-[w
X
v]
Not
Associative:
[U
X
[V
X
w]]
#
[[u
X
V]
X
W]
Distributive:
[{u
+
v}
X
wl
=
[u
X
w]
+
[v
X
w]
Multiple Products of Vectors
Somewhat more complicated are multiple products formed by combinations of the mul-
tiplication processes just described:
The geometrical interpretations of the first three of these are straightforward. The magni-
tude of
(u
.
[v
X
w])
can easily be shown to represent the volume of a parallelepiped
with edges defined by the vectors
u,
v,
and
w.
EXERCISES
I.
What are the "orders" of the following quantities:
(v
-
w), (v
-
u)w,
(ab:cd),
[v
.
pwu],
[[a
X
f]
x
[b
x
gll?
2.
Draw a sketch to illustrate the inequality in
Eq.
A.l-9. Are there any special cases for which it
becomes an equality?
3.
A mathematical plane surface of area S has an orientation given by a unit normal vector
n,
pointing downstream of the surface.
A
fluid of density p flows through this surface with
a
ve-
locity v. Show that the mass rate of flow through the surface is
w
=
p(n
-
v)S.
4.
The angular velocity
W
of a rotating solid body is a vector whose magnitude is the rate of
an-
gular displacement (radians per second) and whose direction is that in which a right-handed
screw would advance if turned in the same direction. The position vector
r
of a point is the
vector from the origin of coordinates to the point. Show that the velocity of any point in
a
ro-
tating solid body is
v
=
[W
X
rl,
relative to an origin located on the axis of rotation.
5.
A constant force
F
acts on a body moving with a velocity
v,
which is not necessarily collinear
with
F.
Show that the rate at which
F
does work on the body is
W
=
(F
.
v).
5A.2 VECTOR OPERATIONS IN TERMS
OF
COMPONENTS
In this section a parallel analytical treatment is given to each of the topics presented geo-
metrically in sA.1. In the discussion here we restrict ourselves to rectangular coordinates
and label the axes as
1,
2,
3
corresponding to the usual notation of
x,
y,
z;
only right-
handed coordinates are used.

sA.2 Vector Operations in Terms of Components
811
Many formulas can be expressed compactly in terms of the Kronecker delta
Sii
and the
permutation symbol
sljk
These quantities are defined thus:
6,
=
+I,
ifi
=
j
ifiZj
cijk
=
+I, if ijk
=
123,231, or 312 (A.2-3)
=
-1
,
if ijk
=
321,132, or 213 (A.2-4)
sijk
=
0, if any two indices are alike (A.2-5)
Note also that
qjk.
=
(1/2)(i
-
j)(j
-
k)(k
-
i).
Several relations involving these quantities are useful in proving some vector and
tensor identities
? ?
Note that a three-by-three determinant may be written in terms of the
qjk
The quantity
s,jk
thus selects the necessary terms that appear in the determinant and af-
fixes the proper sign to each term.
The
Unit
Vectors
Let 6,, 62, 63 be the "unit vectors" (i.e., vectors of unit magnitude) in the direction of the
1,2,3 axes1 (Fig. A.2-1). We can use the definitions of the scalar and vector products to
tabulate all possible products of each type
Fig.
A.2-1.
The unit
2
vectors
6,;
each vector
is of unit magnitude
and points in the ith
1
1 1
direction.
'
In most elementary texts the unit vectors are called
i,
j,
k.
We prefer to
use
6,, 6,,
6,
because the
components of these vectors are given by the Kronecker delta. That is, the component of
6,
in the
1-
direction is
S,,
or unity; the component of
6,
in the 2-direction is
SI2
or zero.

812
Appendix A Vector and Tensor Notation
All of these relations may be summarized by the following two relations:
(A.2-14)
in which
aii
is the Kronecker delta, and
eijk
is the permutation symbol defined in the in-
troduction to this section. These two relations enable us to develop analytic expressions
for all the common dot and cross operations. In the remainder of this section and in the
next section, in developing expressions for vector and tensor operations all we do is to
break all vectors up into components and then apply Eqs. A.2-14 and 15.
Expansion of a Vector in Terms of its Components
Any vector v can be completely specified by giving the values of its projections v,, v,, v,,
on the coordinate axes 1,2,3 (Fig. A.2-2). The vector can be constructed by adding vecto-
rially the components multiplied by their corresponding unit vectors:
Note that a vector associates a scalar with each coordinate dire~tion.~ The vi are called the
"components of the vector
v"
and they are scalars, whereas the 6,vi are vectors, which
when added together vectorially give v.
The magnitude of a vector is given by
[v[=v=dv~+v~+v$=
fi
(A.2-17)
Two vectors v and w are equal if their components are equal: v,
=
w,, v2
=
w,, and
v3
=
w3. Also
v
=
-w,
if
vl
=
-wl, and so on.
Addition and Subtraction of Vectors
The sum or difference of vectors
v
and w may be written in terms of components as
Geometrically, this corresponds to adding up the projections of
v
and
w
on each individ-
ual axis and then constructing a vector with these new components. Three or more vec-
tors may be added in exactly the same fashion.
Fig.
A.2-2.
The components
vi
of the vector
v
are the pro-
1
jections of the vector on the coordinate axes
1,2,
and
3.
For a discussion of the relation
of
this definition of a vector to the definition in terms of the
rules
for transformation of coordinates, see
W.
Prager,
Mechanics
of
Continua,
Ginn, Boston
(1961).

5A.2 Vector Operations in Terms of Components
813
Multiplication of a Vector
by
a
Scalar
Multiplication of a vector by a scalar corresponds to multiplying each component of the
vector by the scalar:
Scalar Product (or Dot Product) of Two Vectors
The scalar product of two vectors v and w is obtained by writing each vector in terms of
components according to Eq. A.2-16 and then performing the scalar-product operations
on the unit vectors, using Eq. A.2-14
Hence the scalar product of two vectors is obtained by summing the products of the cor-
responding components of the two vectors. Note that (v
.
v) (sometimes written as v2 or
as
v2)
is a scalar representing the square of the magnitude of v.
Vector Product (or Cross Product) of Two Vectors
The vector product of two vectors v and
w
may be worked out by using Eqs. A.2-16 and
15:
Here we have made use of Eq.
A.2-8.
Note that the ith-component of [v
X
w] is given by
xi
2,
~~~kv~w~;
this result is often used in proving vector identities.
Multiple Vector Products
Expressions for the multiple products mentioned in sA.1 can be obtained by using the
preceding analytical expressions for the scalar and vector products. For example, the
product (u
.
[v
X
wl) may be written
Then, from
Eq.
A.2-8, we obtain
(U
[V
X
wI)
=
The magnitude of
(u
.
[v
X
wl) is the volume of a parellelepiped defined by the vectors
u, v, w drawn from a common origin. Furthermore, the vanishing of the determinant is a
necessary and sufficient condition that the vectors u, v, and
w
be coplanar.
u1
u2
u3
~1
v2 v3
w1
w2
w3
(A.2-23)

814
Appendix A Vector and Tensor Notation
The Position Vector
The usual symbol for the position vector-that is, the vector specifying the location of a
point in spaceis
r.
The components of
r
are then x,, x,, and x3, so that
This is an irregularity in the notation, since the components have a
s
mbol different
from that for the vector. The magnitude of
r
is usually called
r
=
4
+
xz
+x$
and this
r
is the radial coordinate in spherical coordinates (see
Fig.
A.6-1).
+
The analytical expressions for dot and cross products may be used to prove vector identities;
for example, verify the relation
Proof of
a
Vector
Identity
[U
x
[v
x
w]]
=
V(U
-
W)
-
W(U
-
v) (A.2-25)
SOLUTION
The i-component of the expression on the left side can be expanded as
We may now use
Eq.
A.2-7 to complete the proof
which is just the i-component of the right side of Eq. A.2-25. In a similar way one may verify
such identities as
(U
[v
X
w])
=
(v [w
X
u])
(A.2-28)
([u
X
v]
,
[W
X
z])
=
(U
w)(v
.
z)
-
(u z)(v
-
w)
(A.2-29)
[[u
X
V]
X
[W
X
z]]
=
([u
X
vl
Z)W
-
([u
X
v] w)z
(A.2-30)
EXERCISES
1.
Write out the following summations:
A vector v has components
v,
=
1,
vy
=
2,
v,
=
-5. A vector w has components
w,
=
3,
w,
=
-1,
w,
=
1.
Evaluate:
(a)
(V
W)
(b)
[v
x
wl
(c)
The length of v
(d)
(61
.
V)
(4
[61
x
wl
(f
4"W
(g)
[r
X
v],
where r is the position vector.

3A.3 Tensor Operations in Terms of Components
815
4.
Show that
Eq.
A.2-6 is valid for the particular case
i
=
1,
h
=
2.
Show that
Eq.
A.2-7 is valid for the particular case
i
=
j
=
m
=
1,
n
=
2.
5.
Verify that
zy==,
xi_,
qjkcyk
=
0
if
ajk
=
akv
6.
Explain carefully the statement after
Eq.
A.2-21 that the ith component of
[v
X
wl is
Ej
Ek
&llkv1wk.
7.
Verify that
([v
X
w]
[v
X
w])
+
(v
-
w)'
=
v2w2
(the "identity of Lagrange").
sA.3
TENSOR OPERATIONS IN TERMS OF COMPONENTS
In the last section we saw that expressions could be developed for all common dot and
cross operations for vectors by knowing how to write a vector
v
as a sum
zi
ijivi, and by
knowing how to manipulate the unit vectors tji. In this section we follow a parallel pro-
cedure. We write a tensor
T
as a sum
zi
xj
tiiZijrij, and give formulas for the manipulation
of the unit dyads in this way, expressions are developed for the commonly occur-
ring dot and cross operations for tensors.
The
Unit
Dyads
These results are easy to remember: one simply takes the dot (or cross) product of the
nearest unit vectors on either side of the dot (or cross); in
Eq.
A.3-1 two such operations
are performed.
The unit vectors 6i were defined in the preceding discussion and then the
scalar p~oducts
(tii
tij) and
vector products
[ai
X
Sj] were given. There is a third kind of product that can
be formed with the unit vectors-namely, the
dyadic products
6i6j (written without multi-
plication symbols). According to the rules of notation given in the introduction to Ap-
pendix A, the products are tensors of the second order. Since
tii
and tij are of unit
magnitude, we will refer to the products tji6, as
unit
dyads.
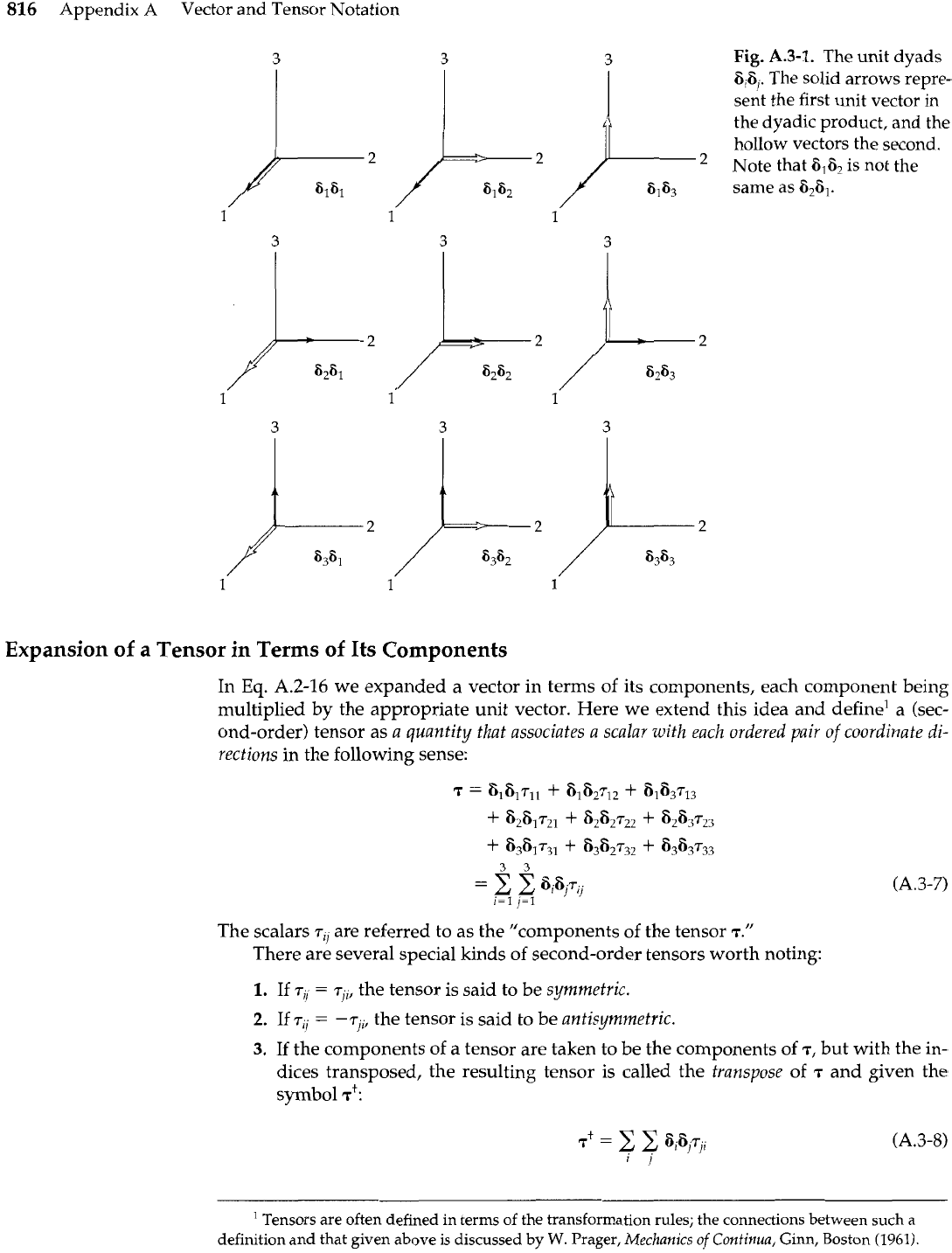
Whereas each unit vector in
Fig. A.2-1 represents a single coordinate direction, the unit dyads in Fig. A.3-1 represent
ordered
pairs of coordinate directions.
(In physical problems we often work with quantities that require the simultaneous
specification of two directions. For example, the flux of x-momentum across a unit area
of surface perpendicular to the
y
direction is a quantity of this type. Since this quantity is
sometimes not the same as the flux of y-momentum perpendicular to the x direction, it is
evident that specifying the two directions is not sufficient;
we
must also agree on the
order in which the directions are given.)
The dot and cross products of unit vectors were introduced by means of the geomet-
rical definitions of these operations. The analogous operations for the unit dyads are in-
troduced formally by relating them to the operations for unit vectors
(6i61:6k61)
=
(6,
'
6k)(6i
'
61)
=
6jksil
(A.3-1)
816
Appendix A Vector and Tensor Notation
Fig.
A.3-1.
The unit dyads
jP2
)L2
)-
&ti,.
The solid arrows repre-
sent the first unit vector in
the dyadic product, and the
hollow vectors the second.
Note that
6,6,
is not the
6161 6162 6163
same as
€i26,.
1 1
1
3
3 3
Expansion of a Tensor in Terms of Its Components
In
Eq.
A.2-16
we expanded a vector in terms of its components, each component being
multiplied
by
the appropriate unit vector. Here we extend this idea and define' a (sec-
ond-order) tensor as
a quantity that associates a scalar with each ordered pair of coordinate di-
rections
in the following sense:
The scalars
rij
are referred to as the "components of the tensor 7."
There are several special kinds of second-order tensors worth noting:
1.
If
rii
=
rj,,
the tensor is said to be
symmetric.
2.
If
rii
=
-T~~,
the tensor is said to be
antisymmetric.
3.
If the components of a tensor are taken to be the components of T, but with the in-
dices transposed, the resulting tensor is called the
transpose
of
T
and given the
symbol I+:
'
Tensors are often defined in terms of the transformation rules; the connections between such a
definition and that given above is discussed
by
W.
Prager,
Mechanics of Continua,
Ginn, Boston
(1961).
