Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


sB.5
The
Equation of Motion in Terms of
7
847
9B.5
THE EQUATION OF MOTION IN TERMS OF
T
Cartesian coordinates
(x,
y,
z):
a
"
These equations have been written without making the assumption that
7
is symmetric. This means, for
example, that when the usual assumption is made that the stress tensor is symmetric,
7,
and
ry,
may be
interchanged.
Cylindrical coordinates
(r,
8, z):~
dv0
V~V,
"+rv@)
[:
:r
av,+v-+9-+v
+
=---
-
+
-
I
-
d
+
-
d
~~0
+
'dr rd0 "dz r
-
-
r
de
a2
These equations have been written without making the assumption that
7
is symmetric. This means, for example, that when the usual
assumption is made that the stress tensor is symmetric,
rrO
-
=
0.
Spherical coordinates (r, 8,4):'
av, av, v, dv, v, dvr
+
v$
dp
+
'
+
--
+
--
-
--)
=
--
at
dr r d8 r
sin
8
d4
r dr
1
Toe
+
74,
(rOr
sin
0)
+
L-
a
-
(r2rrJ
+
-
-
r
sin
8 88 r
sm
8
d4
r4r
r
1
d
(rer
-
~~0)
-
~44
cot
8
(%
sin
e)
+
---
-
(r3rr,)
+
-
-
r
sin
8
de
r
sin
e
de
r$"
+
r
)
+
P&
+
v,vr
+
v,v,
cot
8
1
dP
r r
sin
8
dg5
1
d
(r,,
-
rr+)
+
740
Cot
6
(q,
sin
8)
+
---
-
r
sin
8 d8
r
sin
8
'"
+
r
]
+
P84
These equations have been written without malung the assumption that
7
is symmetric. This means, for example, that when the usual
assumption
is
made that the stress tensor is symmetric,
T,~
-
r8,
=
0.
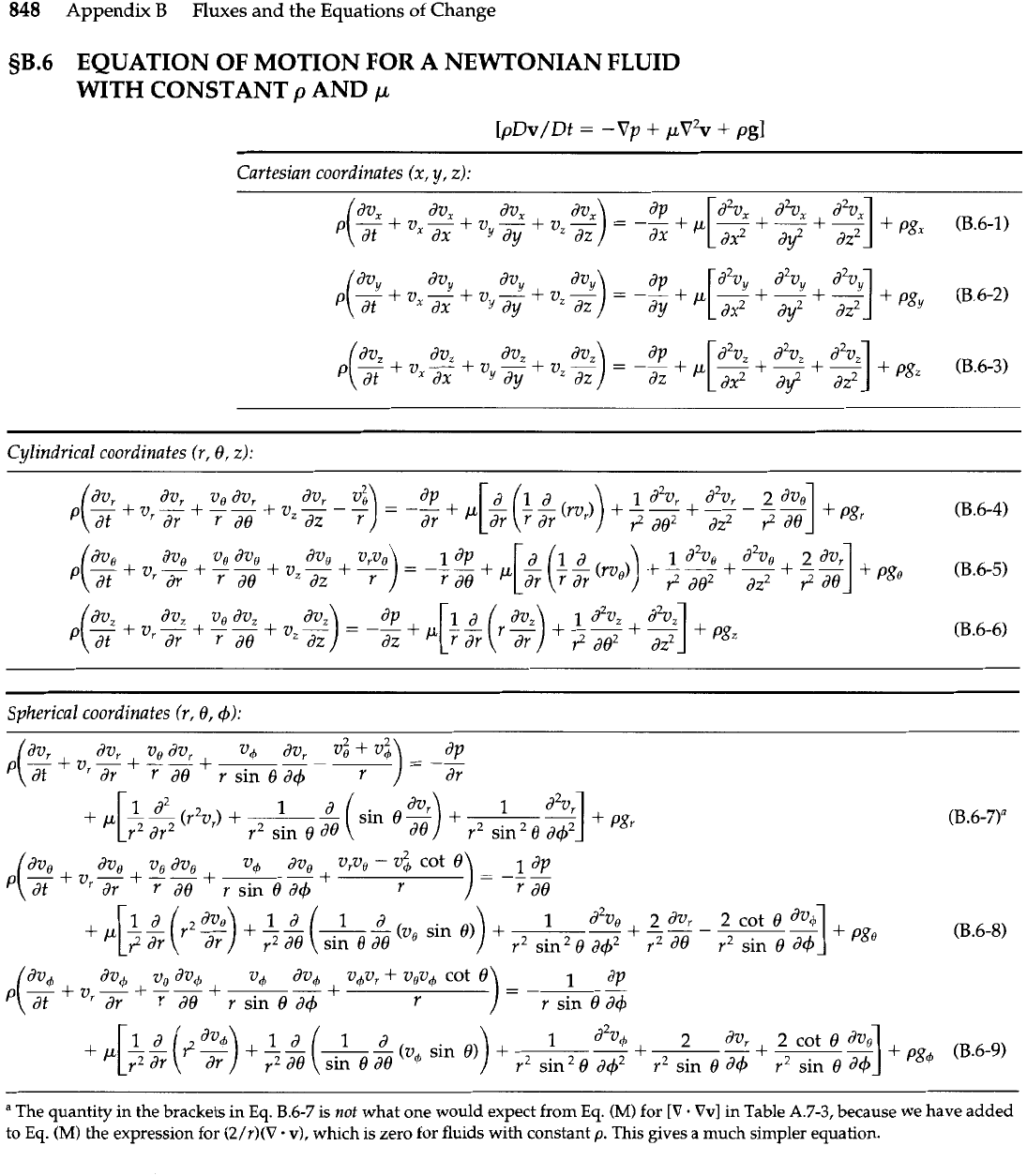
848
Appendix B Fluxes and the Equations of Change
5B.6
EQUATION OF MOTION FOR A NEWTONIAN FLUID
WITH CONSTANT
p
AND
p
[pDv/ Dt
=
-
Vp
+
pV2v
+
pg]
Cartesian coordinates (x,
y,
2):
d
t
+
pgx (B.6-1)
dv, dv, dv,
p(-+vx-+
v
-
+
V,
-
=
-
+
p
+
+
+
pgz (B.6-3)
dt
dx
dy
@)
dz
[
Cylindrical coordinates (r, 6,
z):
1
r2 dr2
r2 sin
B
do
dv, dv, v, dv v+ dv, vp,
-
v: cot 6
p
-fur-+-A+--
+
(
dt dr r
do
r
sin
B
ad r
1 d2v,
2
dv
(v, sin 6)
+
)
r2sin26d~' r2do r2sin6d9
dv+ v dv, v, dv,
+
v+v,
+
v,v+ cot 6 1
dP
p
-+v,-+Ap+--
(dd:
dr r d6 r sin 6
d+
r
r sin 0
d+
(v, sin 6)
+
1
d2v+
dv7
+
%]
+ pg+ (8.64)
+--
)
r2sin28d~' r2sin6M r2sin6d9
a
The quantity in the brackets in Eq.
B.6-7
is
not
what one would expect from
Eq.
(M)
for
[V
.
Vv]
in Table
A.7-3,
because
we
have added
to
Eq.
(M)
the expression for
(2/r)(V
-
v),
which is zero for fluids with constant
p.
This gives a much
simpler
equation.
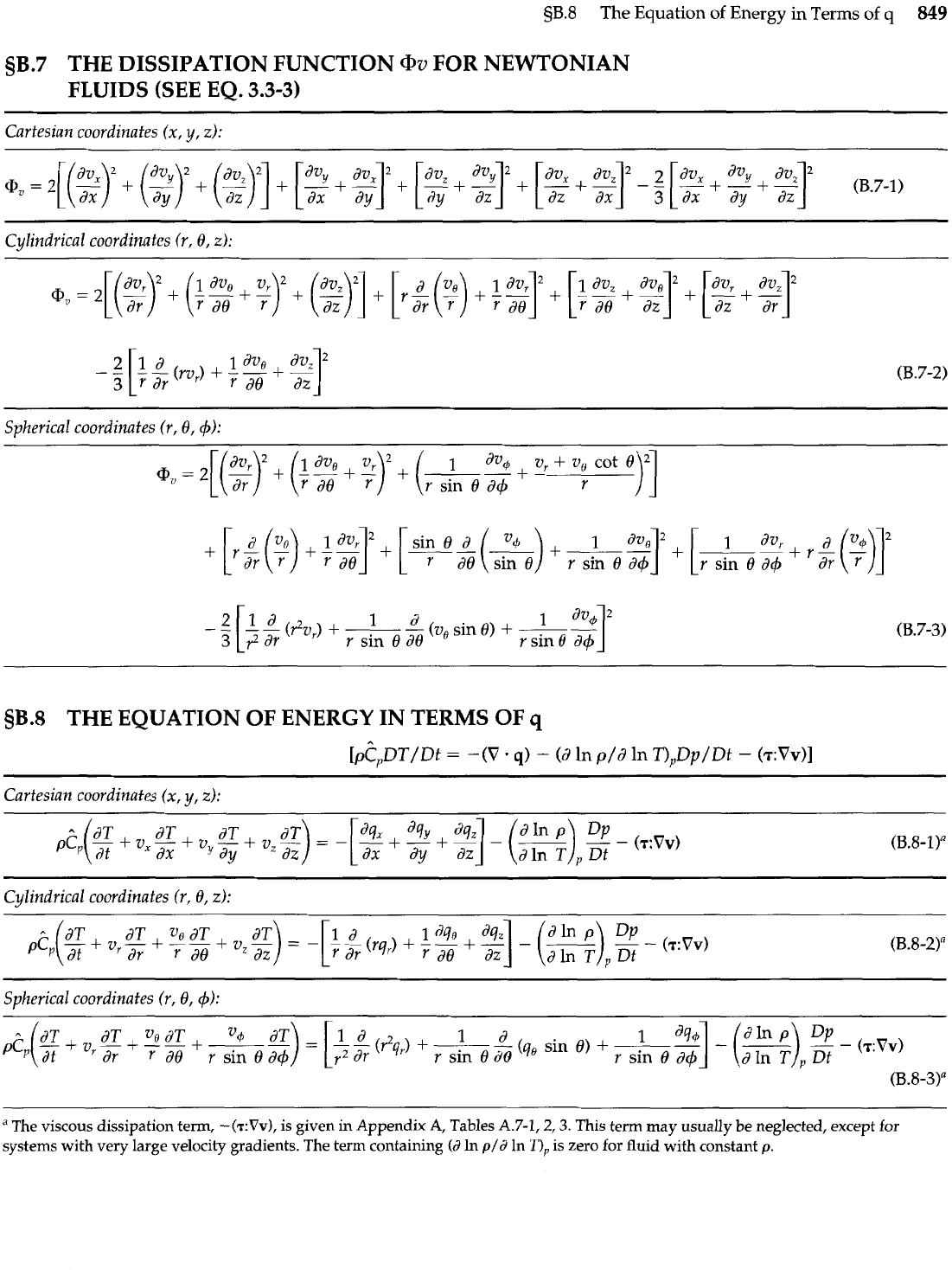
5B.8
The Equation
of
Energy
in
Terms
of
q
849
sB.7
THE DISSIPATION FUNCTION
@v
FOR NEWTONIAN
FLUIDS (SEE EQ.
3.3-3)
-
--
Cartesian coordinates (x,
y,
2):
2
(B. 7-1
)
-
-
Cylindrical coordinates (r, 6,~):
(B.
7-2)
Spherical coordinates (r, 6, 4):
[(:T
(
)
(
I
~V~+V.+V~EO~~
@,=2
-
+
--+-
+
r
sin
6
d4
r
1
d
-
2
[ld(l'vd
+
--
3
y2dr
r
sin
8 d6
5B.8
THE EQUATION OF ENERGY IN TERMS OF
q
I~?~DT/D~
=
-(V.
q)
-
(d
In
p/d
in
nPDp/Dt
-
(7:Vv)l
-
--
Cartesian coordinates (x, y, 2):
Cylindrical coordinates (r, 6,
z):
d~
vnd~
d~)=[ld
1
dqo dln
p
pc -+v,-+--+v,-
*
P
(dT
at dr r d6 dz r ar r d6 dz
-
-
(rq,)
+
-
-
+
(B.8-2>"
--
-
-
Spherical coordinates (r, 6,4):
"
The viscous dissipation term,
-(T:VV),
is given in Appendix A, Tables
A.7-1,2,3.
This term
may
usually be neglected, except for
systems with very large velocity gradients. The term containing
(d
In
p/d
In
'I),
is zero for fluid with constant
p.

850
Appendix
B
Fluxes and the Equations
of
Change
sB.9
THE EQUATION OF ENERGY FOR PURE NEWTONIAN
FLUIDS WITH CONSTANTa
p
AND
k
Cartesian coordinates (x, y, z):
Cylindrical coordinates (r, 0,~):
Spherical coordinates (r, 8,4):
"
This form of the energy equation is also valid under the less stringent assumptions
k
=
constant and
(d
In
p/d
In
T),,Dp/Dt
=
0.
The
assumption
p
=
constant is given in the table heading because it is the assumption more often made.
The function
@,,
is given in
sB.7.
The term
p@,
is usually negligible, except in systems with large velocity gradients.
sB.10
THE EQUATION OF CONTINUITY FOR SPECIES
a
IN TERMSa OF
ja
[pDo,/Dt
=
-(V
.
j,)
+
r,]
Cartesian coordinafes
(x,
y, z):
Cylindrical coordinafes (r, 8, z):
--
-
Spherical coordinates (r, 8,+):
do,
dw,
us
do,
Urn
1
d.
=
[L
a
(r2j,r)
+
-
fur-+--+---
dt
dr
Y
r
sm
8
a+
r2
dr r
sin
0
('"'
Y
sln
0
aia'i.m]+r,
d+
(8.10-3)
sin
0)
+
-
"
To obtain the corresponding equations in terms of
J,*
make the following replacements:
Replace
P
v

sB.11
The Equation of Continuity for Species
A
in
Terms of
w,
for Constant
p%,,
851
gB.11
THE EQUATION OF CONTINUITY FOR SPECIES
A
IN
TERMS
OF
oA
FOR
CONSTANTa
pBAB
-
-
Cartesian coordinates
(x,
y,
2):
Cylindrical coordinates (r, 19,
z):
Spherical coordinates (r, O,+):
1
r2
sin
0
do
(B.11-3)
"
To obtain the corresponding equations in terms
of
x,,
make
the following replacements:
Replace
P
0,
v
re
N
by
c
X,
V*
R,
-
x,
1
Rp
p=1

Appendix
c
Mathematical Topics
1
Some ordinary differential equations and their solutions
5C.2
Expansions of functions in Taylor series
5C.3
Differentiation of integrals (the Leibniz formula)
3C.4
The gamma function
92.5
The hyperbolic functions
5C.6
The error function
In this appendix we summarize information on mathematical topics (other than vectors
and tensors) that are useful in the study of transport phenomena.'
1
SOME ORDINARY DIFFERENTIAL EQUATIONS
AND THEIR SOLUTIONS
We assemble here a short list of differential equations that arise frequently in transport
phenomena. The reader is assumed to be familiar with these equations and how to solve
them. The quantities
a,
b,
and
c
are real constants and
f
and
g
are functions of
x.
Equation Solution
y
=
C1
cosh
ax
+
C2
sinh
ax
or
Some useful reference books on applied mathematics are: M. Abramowitz and
I.
A. Stegun,
Handbook of Mathematical Functions,
Dover, New York, 9th printing (1973); G. M. Murphy,
Ordinary
Differential Equations and Their Solutions,
Van Nostrand, Princeton,
N.J.
(1960);
J. J.
Tuma,
Engineering
Mathematics Handbook,
3rd edition, McGraw-Hill, New York (1987).

5C.2 Expansions of Functions in Taylor Series
853
Solve the equation n2
+
an
+
b
=
0, and
get the roots n= n+ and n
=
n-. Then (a)
if
n+ and n- are real and unequal,
y
=
Clexp(n+x)
+
C2exp(n-x)
(b)
if n+ and n- are real and equal to n,
y
=
enx(Clx
+
C2)
(c)
if n+ and n are complex: ni
=
p
t
iq,
y
=
ePx(C,
cos qx
+
C2 sin qx)
((2.1-6a)
(C.l-6b)
(C.1-7a)
(C.l-7b)
(C. 1 -7~)
(C.1-8)
(C.l-9)
(C.1-10)
(C.1-11)
(C.1-12)
(C.1-13)
(C.1-14)
y
=
C,x"l
+
C2xn2
+
C3xn3, where the
n,
are the roots of
the equation n(n
-
l)(n
-
2)
+
an(n
-
1)
+
bn
+
c
=
0,
provided that all roots are distinct.
Notes:
"
In Eqs.
C.l-4
and
C.l-6
the decisions as to whether to use the exponential forms or the trigonometric (or
hyperbolic) functions are usually made on the basis of the boundary conditions on the problem or the
symmetry properties of the solution.
Equations
C.l-5
and
C.l-6
are solved by making the substitution
y(x)
=
u(x)/x
and then solving the
resulting equation for
u(x).
In Eqs.
C.1-8
to
C.1-13,
it may be convenient or necessary to change the lower limits of the integrals to
some value other than zero.
5C.2
EXPANSIONS OF FUNCTIONS IN TAYLOR SERIES
In
physical problems we often need to describe a function y(x) in the neighborhood of
some point x
=
x,.
Then we expand the function
y(x)
in
a
"Taylor series about the point
x
=
xo":

854
Appendix
C
Mathematical Topics
The first term gives the value of the function at
x
=
x,.
The first two terms give a straight-
line fit of the curve at
x
=
x,.
The first three terms give a parabolic fit of the curve at
x
=
x,
and so on. The Taylor series is often used when only the first several terms are
needed to describe the function adequately.
Here are a few Taylor series expansions of standard functions about the point
x
=
0:
x x2
X3
eix=lt-+-+-+
...
I!
2!
-
3!
(C.2-2)
x2 x3 x4
ln(l+x)=x--+---+.ee
234
(C.2.3)
x2 x4
x6
erfx=p
1--+---+...
2x
(
1!3 2!5 3!7
(C.2-4)
VG
1
1.1
2
1'1'3x3-...
V"Fi=l+-x-x
+
2 2.4 2.4.6
(C.2-5)
Further examples may be found in calculus textbooks and handbooks. Taylor series can
also be written for functions of two or more variables.
5C.3
DIFFERENTIATION OF INTEGRALS
(THE LEIBNIZ FORMULA)
Suppose we have a function
f
(x,
t)
that depends on a space variable
x
and the time
t.
Then we can form the integral
P(t)
I(t)
=
I
f(x,
t)
dx
(C.3-1)
dt)
which is a function of
t
[see Fig.
C.3-l(a)].
If we want to differentiate this function with
respect to
t
without evaluating the integral, we can use the Leibniz formula
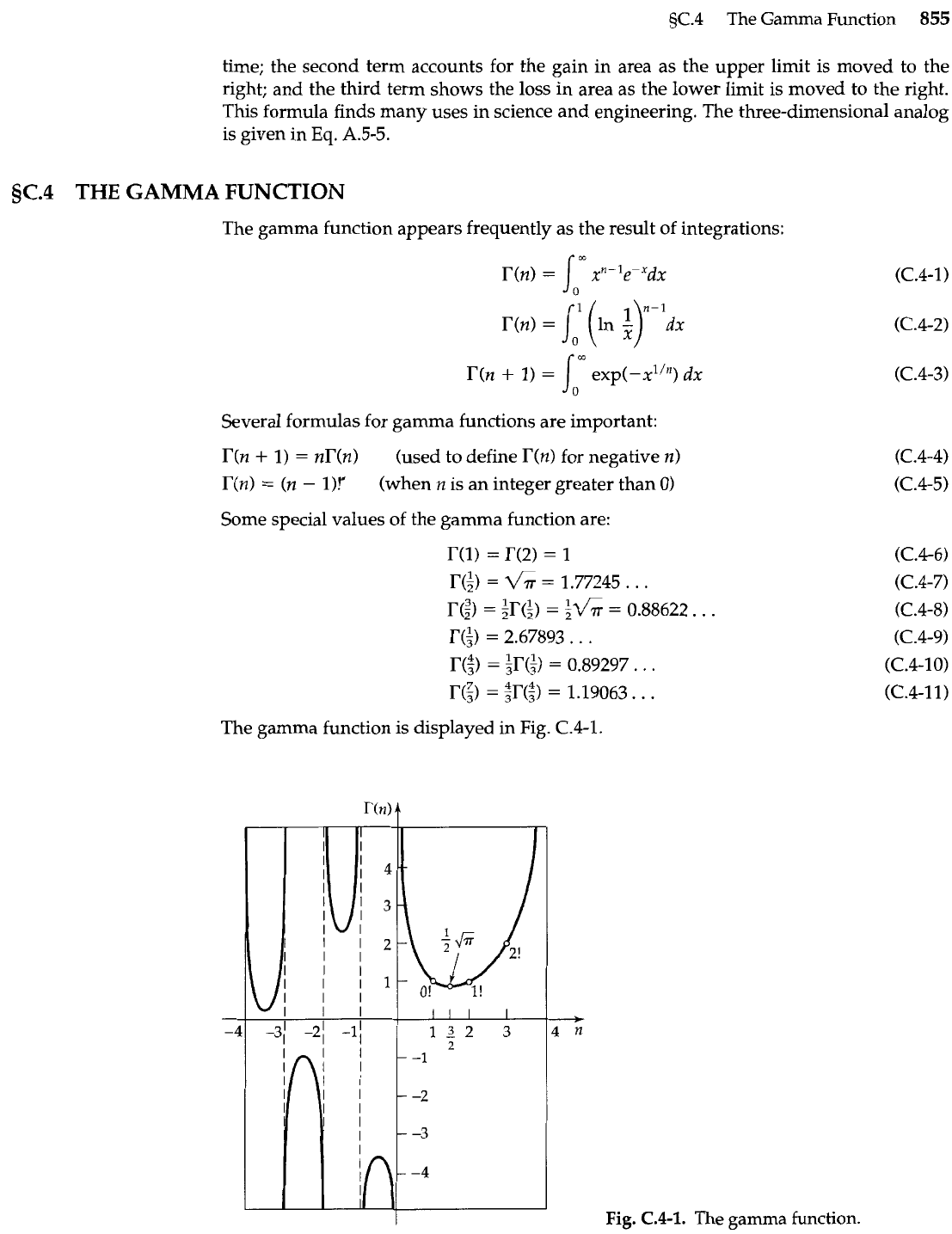
Figure
C.3-l(b)
shows the meanings of the operations performed here: the first term on
the right side gives the change in the integral because the function itself is changing with
a(t) a(t
+
At) P(t) P(t
+
At)
Fig.
C.3-1.
(a)
The shaded area represents
I(t)
=
J
f
(x,
t)dx
at an
df)
instant
t
(Eq. C.3-1).
(b)
To get
dI/dt,
we
form the difference
I(t
+
At)
-
I(t),
divide
by
At,
and then let
At
+
0.
The three shaded
areas correspond to the three terms on the right side of
Eq. C.3-2.
sC.4
The
Gamma Function
855
time; the second term accounts for the gain in area as the upper limit is moved to the
right; and the third term shows the loss in area as the lower limit is moved to the right.
This formula finds many uses in science and engineering. The three-dimensional analog
is given in
Eq.
A.5-5.
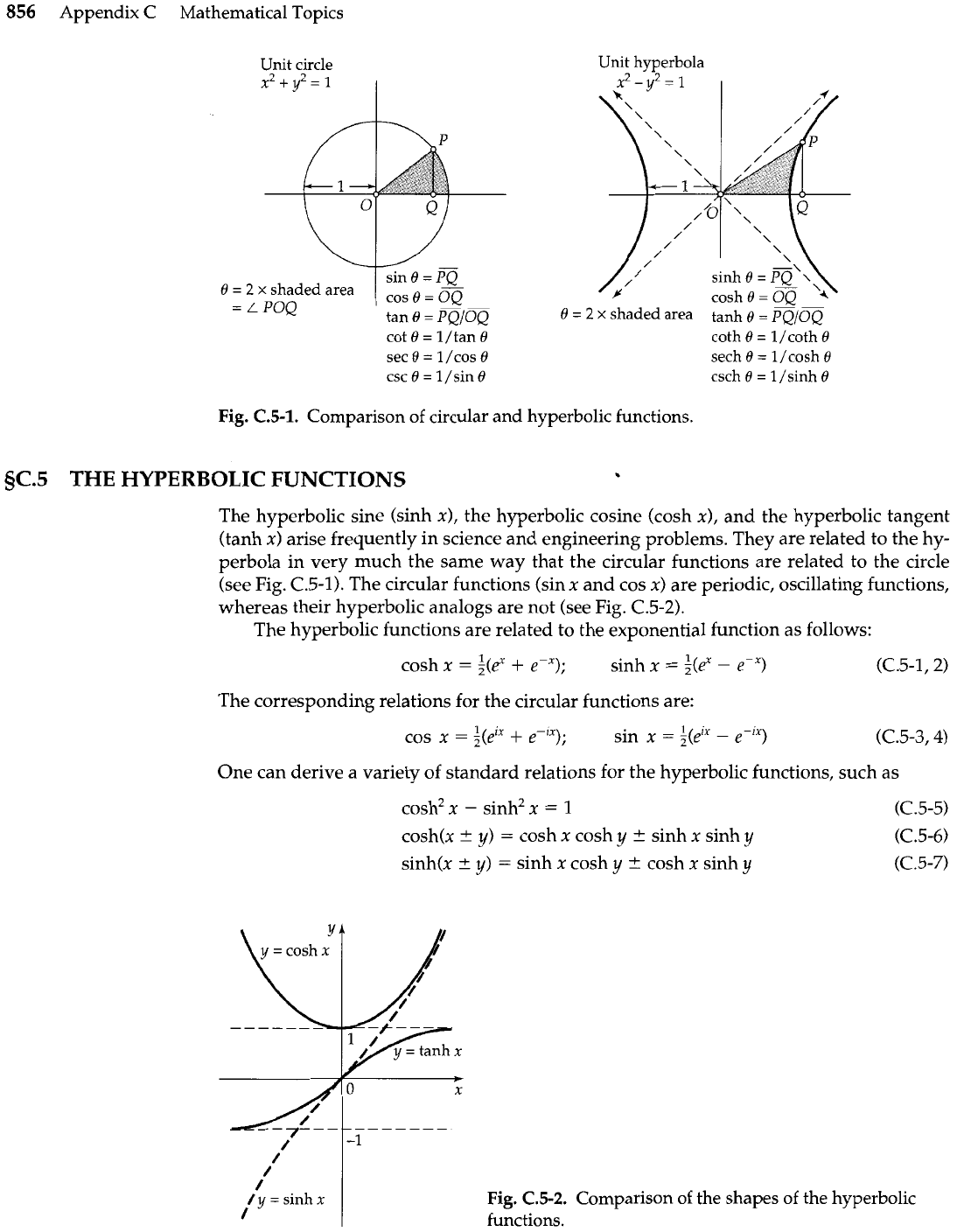
5C.4
THE
GAMMA
FUNCTION
The gamma function appears frequently as the result of integrations:
Several formulas for gamma functions are important:
T(n
+
1)
=
nT(n)
(used to define T(n) for negative n)
T(n)
=
(n
-
l)!'
(when
n
is an integer greater than 0)
The gamma function is displayed in Fig. C.4-1.
+
4
n
Fig. C.4-1.
The
gamma function.
856
Appendix C Mathematical Topics
Unit circle
x2
+
Y2
=
1
6
=
2
x
shaded area
Unit hyperbola
*2-$=
1
=
L
POQ
I
c1
--
--
tan
e
=
PQIOQ
19
=
2
x
shaded area
tanh
9
=
pQ/OQ
cote= l/tanO coth
I9
=
l/coth
I9
sec
6
=
l/cos
6
sech
I9
=
I
/cosh
0
csc 19
=
l/sin
I9
csch
8
=
l/sinh
I9
Fig.
C.5-1.
Comparison of circular and hyperbolic functions.
5C.5
THE
HYPERBOLIC FUNCTIONS
.
The hyperbolic sine (sinh x), the hyperbolic cosine (cosh
x),
and the hyperbolic tangent
(tanh
x)
arise frequently in science and engineering problems. They are related to the hy-
perbola in very much the same way that the circular functions are related to the circle
(see Fig. C.5-1). The circular functions (sin
x
and cos
x)
are periodic, oscillating functions,
whereas their hyperbolic analogs are not (see Fig. C.5-2).
The hyperbolic functions are related to the exponential function as follows:
cosh
x
=
:(e"
+
e-"); sinh
x
=
$(ex
-
e-"1
(C.5-1,2)
The corresponding relations for the circular functions are:
One can derive a variety of standard relations for the hyperbolic functions, such as
cosh2 x
-
sinh2 x
=
1
cosh(x
*
y)
=
cosh x cosh
y
2
sinh
x
sinh
y
sinh(x
?
y)
=
sinh
x
cosh
y
2
cosh x sinh
y
Fig.
C.5-2.
Comparison of the shapes of the hyperbolic
functions.
