Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

5C.6

The Error Function

857

cosh ix

cos x;

sinh

sin x

(C.5-8,9)

cosh x dx

sinh x;

sinh

cosh x (C.5-12,13)

It should be kept in mind that cosh x and cos x are both even functions of x, whereas

sinh

and sin

are odd functions of

5C.6

THE ERROR FUNCTION

The error function is defined as

This function, which arises naturally in numerous transport problems, is monotone in-

creasing, going from erf

to erf

and has the value of 0.99 at about x

The

Taylor series expansion for the error function about

0 is given in

Eq.

C.2-4.

It is also

worth noting that erf

(-x)

-erf x, and that

by applying the Leibniz formula to

Eq.

C.6-1.

The closely related function erfc x

erf

is called the "complementary error

function.''

Appendix

The Kinetic Theory of Gases

5D.1

The Boltzmann equation

9D.2

The equations of change

5D.3

The molecular expressions for the fluxes

5D.4

The solution to the Boltzmann equation

5D.5

The fluxes in terms of the transport properties

5D.6

The transport properties in terms of the intermolecular forces

5D.7

Concluding comments

In Chapters

1,9,

and

we gave a brief account of the use of mean free path arguments

to get approximate expressions for the transport properties. Then we gave the rigorous

results from the Chapman-Enskog development for dilute monatomic gases. In this ap-

pendix we give a brief description of the Chapman-Enskog theory, just enough to show

what the theory involves and to show how it gives a sense of unity to the subject of

transport phenomena in gases. The reader who wishes to pursue the subject further can

consult the standard references.'

THE

BOLTZMANN

EQUATION^

The starting point for the kinetic theory of low-density, nonreacting mixtures of

monatomic gases is the

Boltzmann equation

for the velocity distribution function

t).

The quantity

f&,

dk,dr is the probable number of molecules of species

which at

time

are located in the volume element dr at position

and have velocities within the

range

dib.

about

i.,.

The Boltzmann equation, which describes how

evolves with time, is

Ferziger and

Kaper,

Mathematical Theory of Transport Processes in Gases,

North-Holland,

Amsterdam (1972);

Chapman and

Cowling,

The Mathematical Theory of Non-Uniform Gases,

3rd

edition, Cambridge University Press (1970);

Hirschfelder, C. F. Curtiss, and

Bird,

Molecular

Theory of Gases and Liquids,

2nd corrected printing, Wiley, New York (1964), Chapter 7;

Lifshitz and

Pitaevskii,

Physical Kinetics,

Pergamon, Oxford (1981), Chapter

Boltzmann,

Sitzungsberichte Keiserl. Akad. der Wissenschaften,

(2), 275-370 (1872); C.

Cercignani,

The Boltzmann Equation and Its Applications,

Springer-Verlag, New York (1988).

Curtiss,

Chem. Phys.,

97,1416-1423,7679-7686 (1992), found it necessary to modify the Boltzmann equation to

account for the possibility of orbiting pairs of molecules; the modification, important only at very low

temperatures, was found to give much better agreement with the limited low-temperature experimental

data.

5D.3

Molecular Expressions for the Fluxes

859

in which d/dr is identical to the V-operator, and

d/d&

is a similar operator involving ve-

locities rather than positions. The quantity

is the external force per unit mass acting on

a molecule of species a, and

is a very complicated five-fold integral term accounting

for the change in f, because of molecular collisions. The

term involves the intermolecu-

lar potential energy function (e.g., the Lennard-Jones potential) and the details of the col-

lision trajectories. The Boltzmann equation may be thought of as a continuity equation in

the six-dimensional position-velocity space, and

serves as a source term. The veloc-

ity distribution function is "normalized" to the number density of species

that is,

Sf,(&, r, t)dra

nab t).

5D.2

THE EQUATIONS OF CHANGE

When the Boltzmann equation is multiplied by some molecular property rl/,(r,) and then

integrated over all molecular velocities, the general equation of change is obtained:

An integration by parts is performed to get this result, and use is made of the fact that

is zero at infinite velocities. If

is a quantity that is conserved during a collision (see

§0.3), then the term containing

can be shown to be zero.'

Now let

be successively the conserved quantities for monatomic molecules: the

mass

ma,

the momentum

ma&,

and the energy

$m,(i,

r,). When these are substituted for

into Eq. D.2-1, and when a sum over all species

is performed for the second and

third of these, we get the equations of change for mass of

momentum, and energy as

follows:

In the last of these equations the internal energy per unit volume is defined to be

Thus we see that the equations of continuity, motion, and energy are direct conse-

quences of the conservation laws for mass, momentum, and energy discussed in Chapter

0. Equations D.2-2 to 4 should be compared with Eqs. 19.1-7,3.2-9, and Eq.

(B)

and foot-

note (b) of Table 19.2-4, which were derived by continuum arguments.

5D.3

THE MOLECULAR EXPRESSIONS FOR THE FLUXES

At the same time the equations of change are obtained, the molecular expressions for the

fluxes are generated as integrals over the distribution function:

equilibrium

j,<r, t)

m,S(r,

v)fadr, -0 (D.3-I)

equilibrium

dr,

m$(&

v)(

ib.

v)f,dL

equilibrium

q(r,

$m,J.(ib,

v)'(+,

v)f,dr,

860

Appendix

The Kinetic Theory of Gases

In these expressions the fluxes involve integrals over the products of mass, momentum,

and energy with the "diffusion velocity"

(i;

v) of species

Note the similarity be-

tween the structure of these molecular fluxes (or "diffusive fluxes") and that of the con-

vective fluxes of mass p,v, momentum pw, and kinetic energy ipv2v appearing in the

equations of change, where v is the local instantaneous mass average velocity of the gas

mixture. Thus the molecular fluxes represent the diffusive movement of mass, momen-

tum, and energy above and beyond that described by the convective fluxes. Note also

that the molecular theory automatically generates the molecular work term

v])

in the energy equation.

5D.4

THE SOLUTION TO THE BOLTZMANN EQUATION

If the gas mixture were at rest, the velocity distribution function would be given by the

Maxwell-Boltzmann distribution function (known from equilibrium statistical mechan-

ics). Then we would find, as shown in 5D.3, that

that

.rr

pi3

n~T6, and that

The derivation of p

is given in Problem 1C.3.

On the other hand, when there are concentration, velocity, and temperature gradi-

ents, the distribution function is given as the Maxwell-Boltzmann distribution multi-

plied by a "correction factor":

where

1. In this expression n,, v, and T are functions of position r and time t.

Since the deviations from equilibrium result from the temperature, velocity, and concen-

tration gradients,

$,(r,,

r, t) can be represented, near equilibrium, as a linear function of

the various gradients,

in which the vector

A,,

the tensor B,, and the vectors Cap, all functions of

r,,

r, and

are

given as the solutions of integrodifferential equations.' The quantities d, are "general-

ized diffusional driving forces" that include concentration gradients, the pressure gradi-

ent, and external force differences, defined as

in which x,,

w,,

and p, are the mole fraction, mass fraction, and partial pressure, respec-

tively. Equation D.4-3, valid only for a mixture of monatomic gases at low density, is

generalized for other fluids in the discussion of the thermodynamics of irreversible

processes in 524.1.

5D.5

THE FLUXES

TERMS OF THE TRANSPORT PROPERTIES

When Eqs. D.4-1 to 3 are substituted into Eqs. D.3-1 to 3, we get the expressions for the

fluxes in terms of d,, Vv, and VT:

5D.7

Concluding Comments

861

In these equations the transport properties appear: the viscosity p, the thermal conduc-

tivity

the multicomponent thermal diffusion coefficients

D:,

and the multicomponent

Fick diffusivities

Dap

(the

Bop

are the Maxwell-Stefan diffusivities, closely related to the

Dm&.

Thus the kinetic theory predicts the "cross effects": the transport of mass resulting

from a temperature gradient (thermal diffusion) and the transport of energy resulting

from a concentration gradient (the diffusion-thermo effect).

The pressure term in Eq. D.5-2 comes from the first term in the expansion in Eq. D.4-

1 (that is, the Maxwell-Boltzmann distribution), and the viscosity term comes from the

second term (that is, the

term containing the gradients). The kinetic theory of

monatomic gases at low density predicts that the dilatational viscosity will be zero.

5D.6

THE TRANSPORT PROPERTIES

TERMS

THE INTERMOLECULAR FORCES

The transport properties in Eqs. D.5-1 to

are given by the kinetic theory as complicated

multiple integrals involving the intermolecular forces that describe binary collisions in

the gas mixture. Once an expression has been chosen for the intermolecular force law

(such as the Lennard-Jones (6-12) potential of Eq. 1.4-lo), these integrals can be evalu-

ated numerically. For a pure gas, the three transport

properties-self-diffusivity,

viscos-

ity, and thermal conductivity-are then given by:

The dimensionless "collision integrals"

flk

1.1% contain all the information

about the intermolecular forces and the binary collision dynamics. They are given in

Table E.2 as functions of

KT/&.

If we set the collision integrals equal to unity, we then get

the transport properties for a gas composed of rigid spheres.

Thus the transport properties, needed in the equations of change, have been obtained

from kinetic theory in terms of the two parameters

an<

of the in_termolecular potential

energy function. From these expressions we get Pr

C,p/k

$(c,/C,)

$(;)

and

p/p9

z(fl,/o,)

these values being quite

good for pure monatomic gases.

sD.7

CONCLUDING COMMENTS

The above discussion emphasizes the close connections among mass, momentum, and

energy transport, and it is seen how all three transport phenomena can be explained

terms of a molecular theory for low-density, monatomic gases. It is also important to see

that the continuum equations of continuity, motion, and energy can all be derived from

one starting point-the Boltzmann equation-and that the molecular expressions for the

fluxes and transport properties are generated in the process. In addition, the discussion

of the dependence of the fluxes on the driving forces is very closely related to the irre-

versible thermodynamics approach in Chapter

24.

This appendix has dealt only with low-density, monatomic gases. Similar discus-

Curtiss,

Chem. Phys.,

24,225-241 (1956);

C. Muckenfuss and C.

Curtiss,

Chem. Phys.,

29,

1257-1277 (1958);

Viehland and

Curtiss,

Chem. Phys.,

60,492-520 (1974);

Russell and

Curtiss,

Chem. Phys.,

60,514-520 (1974).

Irving and

Kirkwood,

Chem. Phys.,

18,817-829 (1950);

Bearman and

Kirkwood,

Chem. Phys.,

28,136-145 (1958).

C. F.

Curtiss and

B. Bird,

Adv. Polymer Sci.,

125, 1-101 (1996);

Proc.

Nat.

Acad. Sci.,

93,7440-7445

(1996);

Chem. Phys.,

106,9899-9921 (1997), 107,5254-5267 (1997), 111,10362-10370 (1999).

862

Appendix

The Kinetic Theory of Gases

sions are available for polyatomic gases? monatomic liquids? and polymeric liquids5 In

kinetic theories for monatomic liquids, the expressions for the momentum and heat

fluxes contain terms similar to those in Eqs. D.3-2 and 3, but also contributions associ-

ated with forces between molecules; for polymers, one has the latter contribution, but

also additional forces within the polymer chain. In all of these theories one can derive

the equations of change from an equation for a distribution function and then get formal

expressions for the transport properties.

Appendix

Tables

for

Prediction

Transport Properties

Intermolecular force parameters and critical properties

5E.2

Functions for prediction of transport properties of gases at low densities

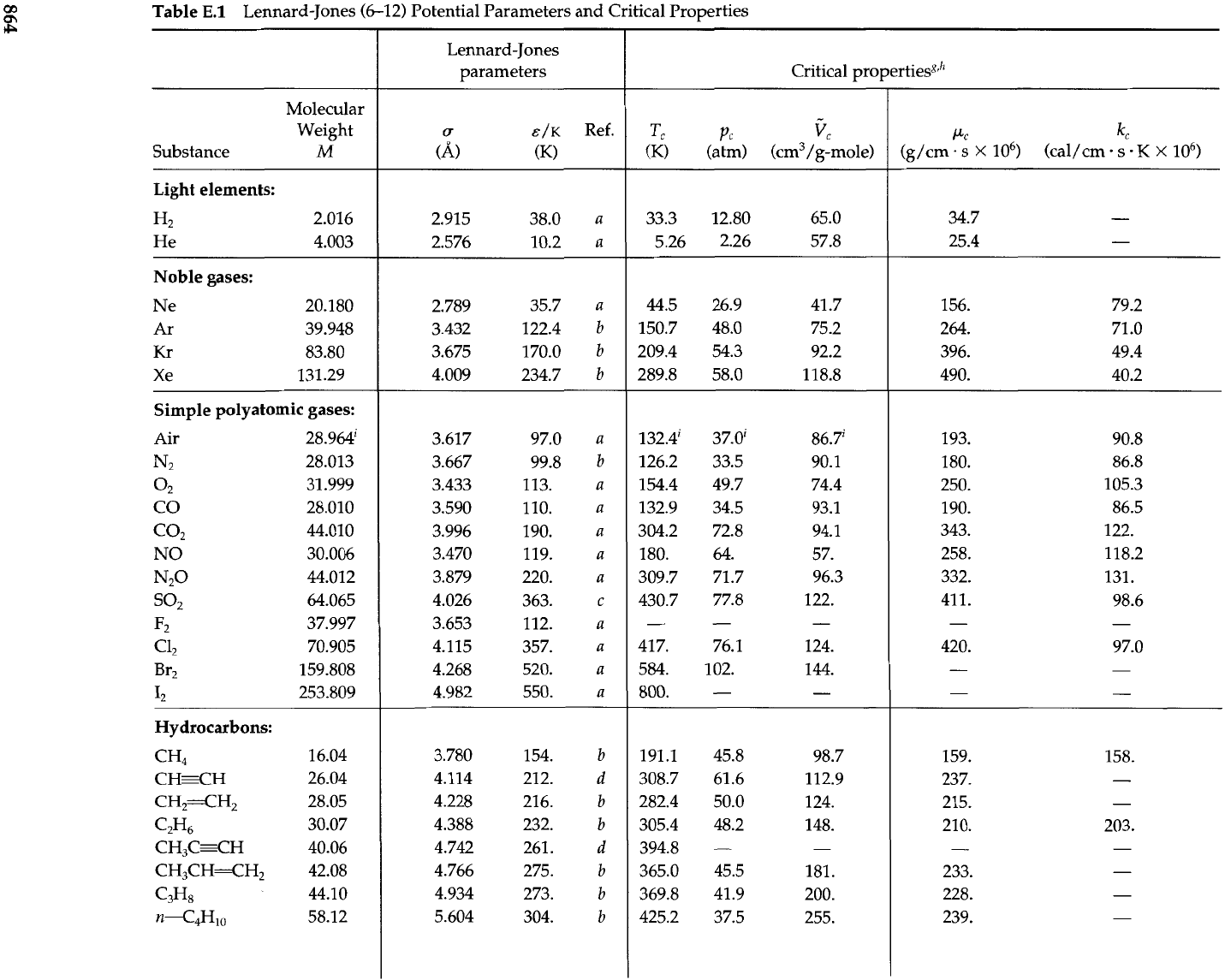
Table

E.l

Lennard-Jones (6-12) Potential Parameters and Critical Properties

Molecular

Weight

Substance

Light elements:

H2 2.016

He 4.003

Noble gases:

Ne 20.180

Ar 39.948

83.80

Xe 131.29

Simple polyatomic gases:

Air 28.9~~

28.013

31.999

CO 28.010

co2

44.010

NO 30.006

44.012

so2

64.065

F2 37.997

c12

70.905

Br2 159.808

12 253.809

Hydrocarbons:

CH4

CHgH

CH2=CH2

C2H6

CH,C=CH

CH3CH=CH2

C3H8

n--C4H10

Lennard-Jones

parameters

E/K

Ref.

(A,

(K)

Critical properties8,h

(K) (atm) (cm3/g-mole)

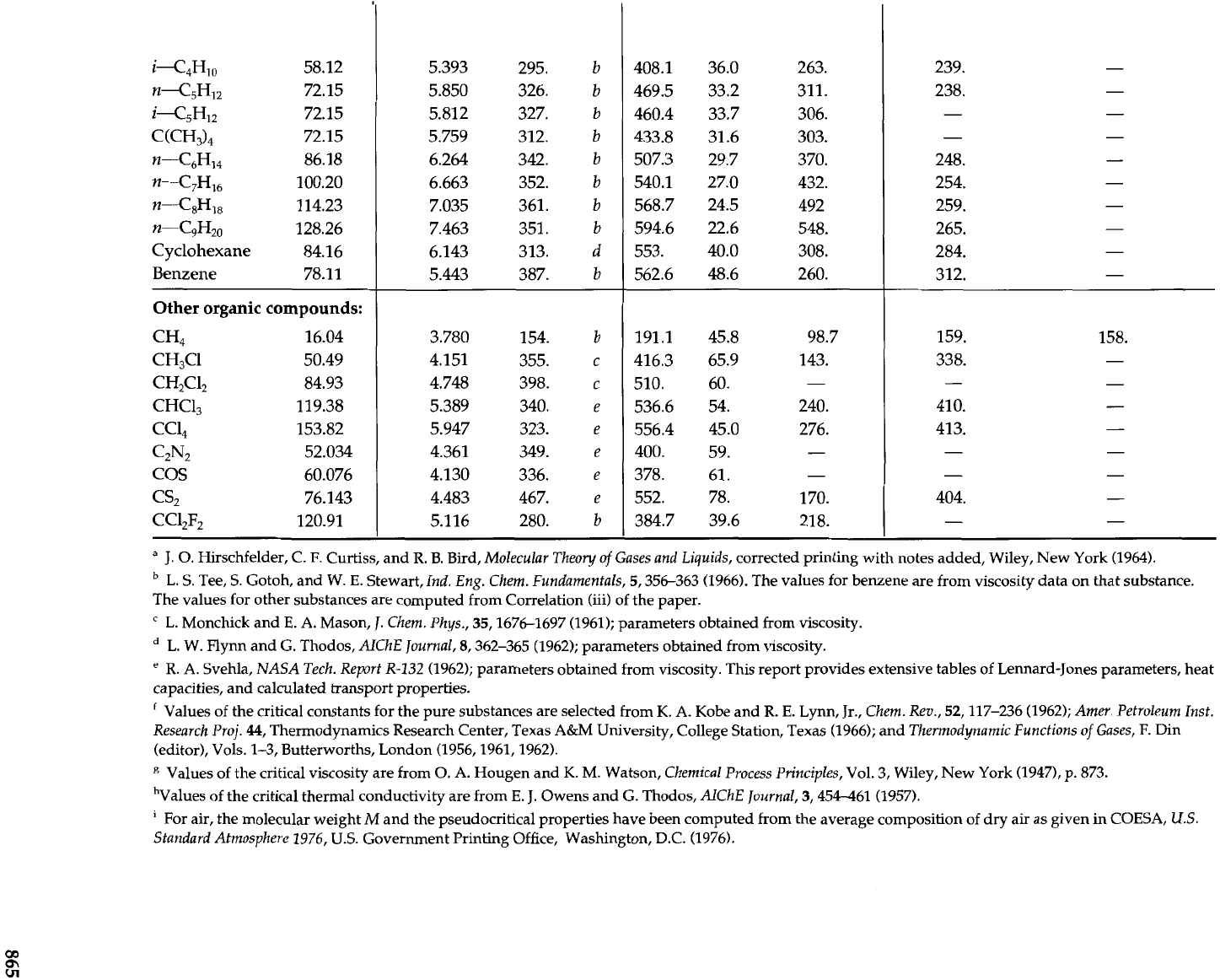
Other

organic compounds:

cH4 16.04

CH3C1 50.49

CH2C12 84.93

CHC1, 119.38

CCl, 153.82

C2N2 52.034

COS 60.076

cs2

76.143

CC12F2 120.91

0. Hirschfelder, C.

Curtiss, and

B. Bird,

Molecular Theoy of Gases and Liquids,

corrected printing with notes added, Wiley, New York (1964).

S. Tee,

Gotoh, and

Stewart,

Ind. Eng. Chem. Fundamentals,

5,356-363 (1966). The values for benzene are from viscosity data on that substance.

The values for other substances are computed from Correlation (iii) of the paper.

Monchick and

Mason,

Chem. Phys.,

35,1676-1697 (1961); parameters obtained from viscosity.

L. W. Flynn and

Thodos,

AIChE

Journal,

8,362-365 (1962); parameters obtained from viscosity.

Svehla,

NASA Tech. Report

R-132

(1962); parameters obtained from viscosity. This report provides extensive tables of Lennard-Jones parameters, heat

capacities, and calculated transport properties.

Values of the critical constants for the pure substances are selected from

Kobe and

Lynn, Jr.,

Chem. Rev.,

52,117-236 (1962);

Amer. Petroleum Inst.

Research Proj.

44,

Thermodynamics Research Center, Texas A&M University, College Station, Texas (1966); and

Thermodynamic Functions

Gases,

F. Din

(editor), Vols. 1-3, Butterworths, London (1956,1961,1962).

Values of the critical viscosity are from

Hougen and

Watson,

Chemical Process Principles,

Vol.

Wiley, New York (1947),

873.

hValues of the critical thermal conductivity are from

Owens and

Thodos,

AlChE Journal,

3,454-461 (1957).

For air, the molecular weight

and the pseudocritical properties have been computed from the average composition of dry air as given in COESA,

U.S.

Standard Atmosphere

1976,

U.S.

Government Printing Office, Washington, D.C. (1976).

Table

E.2

Collision Integrals for Use with the Lennard-Jones

(6-12)

Potential for the

Prediction of Transport Properties of Gases at Low ~ensities",~,'

KT/&

(for viscosity

%AB

or and thermal (for

KT/&~,

conductivity) diffusivity)

I(Zk

KT/&

(for viscosity

%,A,

or and thermal (for

KT/E~~

conductivity)

diffusivity)

The values in this table, applicable for the Lennard-Jones (6-12) potential, are interpolated from the results of

Monchick and

A. Mason,

Chem. Phys.,

35,1676-1697 (1961). The Monchick-Mason table is believed to be slightly

better than the earlier table by

Hirschfelder,

R. B.

Bird, and

Spotz,

Chem.

Phys.,

16,968-981 (1948).

This table has been extended to lower temperatures by C.

Curtiss,

Chem. Phys.,

97,7679-7686 (1992). Curtiss

showed that at low temperatures, the Boltzmann equation needs to be modified to take into account "orbiting pairs"

of molecules. Only by making this modification is it possible to get a smooth transition from quantum to classical

behavior. The deviations are appreciable below dimensionless temperatures of 0.30.

'The collision integrals have been curve-fitted by

Neufeld, A.

Jansen, and

A. Aziz,

Chem. Phys.,

57,

1100-1102 (1972), as follows:

where

KT/&.