Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

Problems

327

the temperatures at the inner and outer walls being To and TI. The thermal conductivity of the

insulation varies linearly with temperature from

at To to

TI.

(b)

Estimate the rate of evaporation of liquid oxygen from a spherical container of

ft inside

diameter covered with a 1-ft-thick annular evacuated jacket filled with particulate insulation.

The following information is available:

Temperature at inner surface of insulation

183°C

Temperature at outer surface of insulation 0°C

Boiling point of

183°C

Heat of vaporization of

1636 cal/g-mol

Thermal conductivity of insulation at 0°C

9.0

Btu/hr ft

Thermal conductivity of insulation at -183°C

7.2

Btu/hr. ft

Answers: (a)

4morl

(

)(

(b)

0.198 kghr

10B.15.

Radial temperature gradients in an annular chemical reactor. A catalytic reaction is being

carried out at constant pressure in a packed bed between coaxial cylindrical walls with inner

radius ro and outer radius

r,.

Such a configuration occurs when temperatures are measured

with a centered thermowell, and is

addition useful for controlling temperature gradients if

a thin annulus is used. The entire inner wall is at uniform temperature To, and it can be as-

sumed that there is no heat transfer through this surface. The reaction releases heat at a uni-

form volumetric rate

throughout the reactor. The effective thermal conductivity of the

reactor contents is to be treated as a constant throughout.

(a) By a shell energy balance, derive a second-order differential equation that describes the

temperature profiles, assuming that the temperature gradients in the axial direction can be

neglected. What boundary conditions must be used?

(b)

Rewrite the differential equation and boundary conditions in terms of the dimensionless

radial coordinate and dimensionless temperature defined as

Explain why these are logical choices.

(c)

Integrate the dimensionless differential equation to get the radial temperature profile. To

what viscous flow problem is this conduction problem analogous?

(d)

Develop expressions for the temperature at the outer wall and for the volumetric average

temperature of the catalyst bed.

(e)

Calculate the outer wall temperature when r,

0.45 in., r,

0.50

in.,

k,,

0.3 Btu/hr. ft

900°F, and

4800 cal/hr cm3.

(f)

How would the results of part (e) be affected if the inner and outer radii were doubled?

Answer: (e) 888°F

10B.16.

Temperature distribution in a hot-wire anemometer. A hot-wire anemometer is essentially

a fine wire, usually made of platinum, which is heated electrically and exposed to a flowing

fluid. Its temperature, which is a function of the fluid temperature, fluid velocity, and the rate

of heating, may be determined by measuring its electrical resistance. It is used for measuring

velocities and velocity fluctuations in flow systems. In this problem we analyze the tempera-

ture distribution in the wire element.

We consider a wire of diameter

and length

supported at its ends

-L

and

+L)

and mounted perpendicular to an air stream. An electric current of density

amp/cm2

flows through the wire, and the heat thus generated is partially lost by convection to the air

stream (see Eq. 10.1-2) and partially by conduction toward the ends of the wire. Because of

their size and their high electrical and thermal conductivity, the supports are not appreciably

heated by the current, but remain at the temperature

which is the same as that of the ap-

proaching air stream. Heat loss by radiation is to be neglected.

328

Chapter 10 Shell Energy Balances and Temperature Distributions in Solids and Laminar Flow

(a) Derive an equation for the steady-state temperature distribution in the wire, assuming

that

depends on

alone; that is, the radial temperature variation in the wire is neglected.

Further, assume uniform thermal and electrical conductivities in the wire, and a uniform heat

transfer coefficient from the wire to the air stream.

(b)

Sketch the temperature profile obtained in (a).

(c)

Compute the current, in amperes, required to heat a platinum wire to a midpoint temper-

ature of 50°C under the following conditions:

20°C h

100 Btu/hr. ft2

0.127 mm

40.2 Btu/hr ft

0.5 cm

1.00

lo5

ohm-' cm-'

Answers: (a)

cOsh?!h!!?);

(c)

1.01 amp

(

coshd4h/k~~

10B.17.

Non-Newtonian

flow

with forced-convection heat transfer? For estimating the effect

non-Newtonian viscosity on heat transfer in ducts, the power law model of Chapter 8 gives

velocity profiles that show rather well the deviation from parabolic shape.

(a) Rework the problem of 510.8 (heat transfer in

circular

tube)

for the power law model

given in Eqs.

8.3-2,3.

Show that the final temperature profile is

in which s

/n.

(b)

Rework Problem 10B.7 (heat transfer in a plane slit) for the power law model. Obtain the

dimensionless temperature profile:

Note that these results contain the Newtonian results (s

and the plug flow results (s

to).

See Problem 10D.2 for a generalization of this approach.

10B.18.

Reactor temperature profiles with axial heat flux2 (Fig. 10B.18).

(a) Show that for a heat source that depends linearly on the temperature, Eqs. 10.5-6 to 14

have the solutions (for m+

m-)

m+m-(exp m+

exp m-)

@'=I+

exp [(m,

m-)Zl

m+ exp m+

m- exp

(exp m+)(exp m-Z)

m- (exp mdexp m+Z)

(m+

m-) (10B.18-2)

m: exp m+

m2_

exp m-

-m-

@"I

exp (m,

m-)

m: exp

m exp

Here

iB(1

(4N/B),

which

pvo~p~/~eff,,,. Some profiles calculated from

these equations are shown in Fig. 108.18.

Bird,

Chem.-Ing. Technik,

31,569-572 (1959).

Taken from the corresponding results of

Damkohler,

Elektrochem.,

43,l-8,9-13 (1937), and

Wehner and

Wilhelm,

Chern.

Engr.

Sci.,

6,89-93 (1956); 8,309 (1958), for isothermal flow reactors

with longitudinal diffusion and first-order reaction. Gerhard Damkohler (190&1944) achieved fame for

his work on chemical reactions in flowing, diffusing systems; a key publication was in

Der Chemie-

Ingenieur,

Leipzig (19371, pp. 359485. Richard

Herman

Wilhelm (1909-1968), chairman of the Chemical

Engineering Department at Princeton University, was well known for his work on fixed-bed catalytic

reactors, fluidized transport, and the "parametric pumping" separation process.

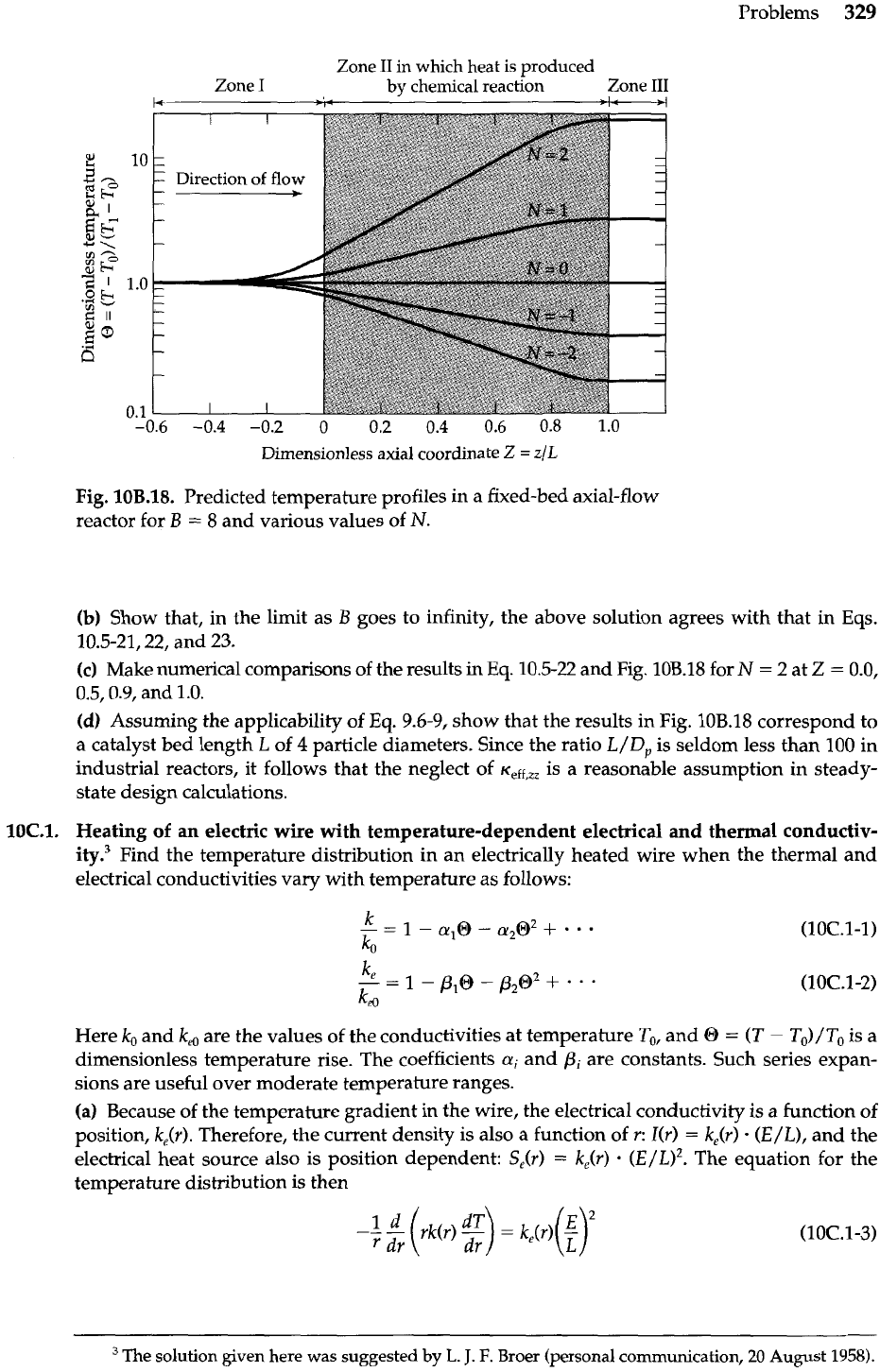
Problems

329

Zone

which heat

produced

Zone

chemical reaction Zone

I11

-0.6 -0.4 -0.2 0 0.2 0.4

0.6

0.8 1.0

Dimensionless

axial

coordinate

z/L

Fig.

10B.18.

Predicted temperature profiles in a fixed-bed axial-flow

reactor for

8 and various values of

(b)

Show that, in the limit as

goes to infinity, the above solution agrees with that in Eqs.

10.5-21,22, and

23.

(c)

Make numerical comparisons of the results

Eq. 10.5-22 and Fig. 10B.18 for

2 at

0.0,

0.5,0.9, and

1.0.

(dl

Assuming the applicability of

Eq.

9.6-9, show that the results in Fig. 10B.18 correspond to

a catalyst bed length

particle diameters. Since the ratio

LID,

is seldom less than 100 in

industrial reactors, it follows that the neglect of

K,,,,~,

is a reasonable assumption in steady-

state design calculations.

10C.l.

Heating of an electric wire with temperature-dependent electrical and thermal conductiv-

it^.^

Find the temperature distribution in an electrically heated wire when the thermal and

electrical conductivities vary with temperature as follows:

Here

and

are the values of the conductivities at temperature

To,

and

To)/To

is a

dimensionless temperature rise. The coefficients

and

are constants. Such series expan-

sions are useful over moderate temperature ranges.

(a)

Because of the temperature gradient in the wire, the electrical conductivity is a function of

position,

k,(r).

Therefore, the current density is also a function of

I(r)

ke(r)

(EIL),

and the

electrical heat source also is position dependent:

Se(r)

k,(r) (EIL)'.

The equation for the

temperature distribution is then

---

The

solution given here was suggested

Broer (personal communication,

August

1958).

330

Chapter 10

Shell Energy Balances and Temperature Distributions in Solids and Laminar Flow

Now introduce the dimensionless quantities

r/R

and

kJ?.2E2/k,,~2~o

and show that

Ea. 10C.l-3 then becomes

When the power series expressions for the conductivities are inserted into this equation we get

This is the equation that is to be solved for the dimensionless temperature distribution.

(b)

Begin by noting that if all the

and

were zero (that is, both conductivities constant),

then Eq. 10C.l-5 would simplify to

When this is solved with the boundary conditions that

finite at

0,-and

0 at

we get

$B(l

(lOC.l-7)

This is Eq. 10.2-13 in dimensionless notation.

Note that Eq. 10C.-5 will have the solution in Eq. 10C.l-7 for small values of B-that

is,

for weak heat sources. For stronger heat sources, postulate that the temperature distribution

can be expressed as a power series in the dimensionless heat source strength B:

Here the

are functions of

but not of

Substitute

Eq.

10C.1-8 into Eq. 10C.l-5, and equate

the coefficients of like powers of

to get a set of ordinary differential equations for the

@,,,with

1,2,3,

. .

These may be solved with the boundary conditions that O,,

finite at

0 and

0 at

In this way obtain

where

0(B2)

means "terms of the order of

and higher."

(c)

For materials that are described by the Wiedemann-Franz-Lorenz law (see §9.5), the ratio

k/kJ

is a constant (independent of temperature). Hence

Combine this with Eqs. 10C.l-1 and

to get

Equate coefficients of equal powers of the dimensionless temperature to get relations among

the

and the

Pi:

p,,

and so on. Use these relations to get

10C.2.

Viscous heating with temperature-dependent viscosity and thermal conductivity (Figs.

10.4-1 and

2).

Consider the flow situation shown in Fig. 10.4-2. Both the stationary surface

and the moving surface are maintained at a constant temperature

To.

The temperature depen-

dences of

and

are given by

in which the

and

are constants,

is the fluidity, and the subscript

"0"

means

"evaluated at

To."

The dimensionless temperature is defined as

To)/T,,.

Problems

331

(a) Show that the differential equations describing the viscous flow and heat conduction may

be written in the forms

in which

vz/vb,

and Br

pod/hTo (the Brinkman number).

(b)

The equation for the dimensionless velocity distribution may be integrated once to give

d~$/dt

(v/&,

in which

is an integration constant. This expression is then substituted

into the energy equation to get

Obtain the first two terms of a solution in the form

It is further suggested that the constant of integration

also be expanded as a power series

in the Brinkman number, thus

(c)

Repeat the problem, changing the boundary condition at

(instead of speci-

fying the temperat~re).~

Answers:

(b)

&~rp,(t

35'

2t3)

. .

i~r(t

e2)

t~r~~y,(f

2t3

&~3p~(~

25'

2t3

. .

(c)

:~r~,(2(

35'

Br(&

$5')

~~r'a~(4[~

&~rZp,(-8{

4e3

e4)

10C.3.

Viscous heating in a cone-and-plate viscometer? In Eq. 2B.11-3 there is an expression for

the torque

required to maintain an angular velocity

in a cone-and-plate viscometer

with included angle

t,b0

(see Fig. 2B.11). It is desired to obtain a correction factor to account

for the change in torque caused by the change in viscosity resulting from viscous heating.

This effect can be a disturbing factor in viscometric measurements, causing errors as large

as 20%.

(a) Adapt the result of Problem 10C.2 to the cone-and-plate system as was done in Problem

2B.ll(a). The boundary condition of zero heat flux at the cone surface seems to be more realis-

tic than the assumption that the cone and plate temperatures are the same, inasmuch as the

plate is thermostatted and the cone is not.

(b) Show that this leads to the following modification of Eq. 2B.11-3:

where

pof12R2/koT, is the Brinkman number. The symbol

stands for the viscosity at

the temperature

To.

Turian and

B. Bird,

Chem.

Eng.

Sci.,

18,689-696 (1963).

Turian,

Chem.

Eng.

Sci.,

20,771-781 (1965); the viscous heating correction for non-Newtonian

fluids is discussed in this publication (see also

B. Bird,

Armstrong, and

Hassager,

Dynamics

Polymeric Liquids,

Vol. 1,2nd edition, Wiley-Interscience, New York (1987), pp. 223-227.

332

Chapter 10

Shell Energy Balances and Temperature Distributions in Solids and Laminar Flow

Fig. 10D.l.

Circular fin on a

perature

heated pipe.

Heat loss from a circular

fin

(Fig. 10D.1).

(a)

Obtain the temperature profile

T(r)

for a circular fin of thickness

on a pipe with outside

wall temperature

To.

Make the same assumptions that were made in the study of the rectan-

gular fin in 510.7.

(b)

Derive an expression for the total heat loss from the fin.

Duct flow with constant wall heat

flux

and arbitrary velocity distribution.

(a)

Rework the problem in 510.8 for an arbitrary fully developed, axisyrnrnetric flow velocity

distribution

v,/v,,,,,

4(6),

where

r/R.

venfy that the temperature distribution is given

in which

Show that C1

0 and

[I(l)]-'. Then show that the remaining constant is

Venfy that the above equations lead to Eqs. 10.8-27 to 30 when the velocity profile is parabolic.

These results can be used to compute the temperature profiles for the fully developed

tube flow of any kind of material as long as a reasonable estimation can be made for the

ve-

locity distribution. As special cases, one can get results for Newtonian flow, plug flow, non-

Newtonian flow, and even, with some modifications, turbulent flow (see §13.4).6

(b)

Show that the dimensionless temperature difference driving force

(c)

Verify that the dimensionless wall heat flux is

and that, for the laminar flow of Newtonian fluids, this quantity has the value

(d)

What is the physical interpretation of IU)?

Lyon,

Chem.

Engr.

Prog.,

47,75-59

(1951);

note

that

the

definition of

+(&)

used here is different

from

that

Tables

14.2-1

and

Chapter

The Equations

Change

for

Nonisothermal Systems

911.1 The energy equation

911.2 Special forms of the energy equation

511.3 The Boussinesq equation of motion for forced and free convection

911.4

Use

of the equations of change to solve steady-state problems

511.5 Dimensional analysis of the equations of change for nonisothermal systems

In Chapter 10 we introduced the shell energy balance method for solving relatively sim-

ple, steady-state heat flow problems. We obtained the temperature profiles, as well as

some derived properties such as average temperature and energy fluxes. In this chapter

we generalize the shell energy balance and obtain the equation of energy, a partial differ-

ential equation that describes the transport of energy in a homogeneous fluid or solid.

This chapter is also closely related to Chapter 3, where we introduced the equation

of continuity (conservation of mass) and the equation of motion (conservation of mo-

mentum). The addition of the equation of energy (conservation of energy) allows us to

extend our problem-solving ability to include nonisothermal systems.

We begin in §11.1 by deriving the equation of change for the total energy. As

Chapter 10, we use the combined energy flux vector

in applying the law of conserva-

tion of energy. In 511.2 we subtract the mechanical energy equation (given in 53.3) from

the total energy equation to get an equation of change for the internal energy. From the

latter we can get an equation of change for the temperature, and it is this kind of energy

equation that is most commonly used.

Although our main concern in this chapter will be with the various energy equa-

tions just mentioned, we find it useful to discuss in 511.3 an approximate equation of

motion that is convenient for solving problems involving free convection.

In 511.4 we summarize the equations of change encountered up to this point. Then

we proceed to illustrate the use of these equations in a series of examples, in which we

begin with the general equations and discard terms that are not needed. In this way we

have a standard procedure for setting up and solving problems.

Finally, in 511.5 we extend the dimensional analysis discussion of 53.7 and show

how additional dimensionless groups arise in heat transfer problems.

$11.1

THE

ENERGY

EQUATION

The equation of change for energy is obtained by applying the law of conservation of en-

ergy to

small element of volume

(see Fig. 3.1-1) and then allowing the dimen-

sions of the volume element to become vanishingly small. The law of conservation of

334

Chapter 11 The Equations of Change for Nonisothermal Systems

energy is an extension of the first law of classical thermodynamics, which concerns the

difference in internal energies of two equilibrium states of a closed system because

the heat added to the system and the work done on the system (that is, the familiar

Au=Q+W).'

Here we are interested in a stationary volume element, fixed in space, through

which a fluid is flowing. Both kinetic energy and internal energy may be entering

and

leaving the system by convective transport. Heat may enter and leave the system by heat

conduction as well. As we saw in Chapter 9, heat conduction is fundamentally a molecu-

lar process. Work may be done on the moving fluid by the stresses, and this, too, is

molecular process. This term includes the work done by pressure forces and by viscous

forces. In addition, work may be done on the system by virtue of the external forces,

such as gravity.

We can summarize the preceding paragraph by writing the conservation of energy

in words as follows:

net rate of kinetic net rate of heat

kinetic and

[nd energy internal addition

[;:=by

molecular

by convective

transport (conduction)

rate of work rate of work

done on system

by molecular

by external

(mechanisms (i.e., by stresses) Lrces (e.g., by gravity)

(11.1-1)

In developing the energy equation we will use the

vector of

Eq.

9.8-5 or

which

in-

cludes the first three brackets on the right side of Eq. 11.1-1. Several comments need

be made before proceeding:

(i)

kinetic energy

we mean that energy associated with the observable motion

the fluid, which is ipv2

gp(v

v),

per unit volume. Here v is the fluid velocity

vector.

(ii) By

internal energy

we mean the kinetic energies of the constituent molecules

cal-

culated in a frame moving with the velocity v, plus the energies associated with

the vibrational and rotational motions of the molecules and also the energies

interaction among all the molecules. It is

assumed

that the internal energy

for

a flowing fluid is the same function of temperature and density as that for

fluid at equilibrium. Keep

mind that a similar assumption is made for the

thermodynamic pressure p(p,

for a flowing fluid.

(iii) The

potential energy

does not appear in

Eq.

11.1-1, since we prefer instead

consider the work done on the system by gravity. At the end of this section,

however, we show how to express this work in terms of the potential energy.

(iv) In Eq. 10.1-1 various

source terms

were included in the shell energy balance.

510.4 the viscous heat source S, appeared automatically, because the mechani-

cal energy terms in

were properly accounted for; the same situation prevails

here, and the viscous heating term -(T:VV) will appear automatically in

Eq.

11.2-1. The chemical, electrical, and nuclear source terms (S,,

S,,

and S,) do

not

appear automatically, since chemical reactions, electrical effects, and nuclear

Silbey

and

A. Albert~,

Physical

Chemistry,

Wiley,

New

York,

3rd

edition

(2001),§2.3.

911.1 The Energy Equation

335

disintegrations have not been included in the energy balance. In Chapter 19,

where the energy equation for mixtures with chemical reactions is considered,

the chemical heat source

appears naturally, as does a "diffusive source

term,"

ZJj,

g,).

We now translate Eq. 11.1-1 into mathematical terms. The rate of increase of kinetic

and internal energy within the volume element Ax

Az is

Here is the internalAenergy per unit mass (sometimes called the "specific internal en-

ergy"). The product

is the internal energy per unit volume, and

$v2

;p(vz

v:)

is the kinetic energy per unit volume.

Next we have to know how much energy enters and leaves across the faces of the

volume element Ax

Az.

Keep in mind that the

vector includes the convective transport of kinetic and internal

energy, the heat conduction, and the work associated with molecular processes.

The rate at which work is done on the fluid by the external force is the dot product

of the fluid velocity v and the force acting on the fluid (p Ax

Az)g, or

We now insert these various contributions into Eq. 11.1-1 and then divide by

Az.

When Ax,

Ay,

and Az are allowed to go to zero, we get

This equation may be written more compactly in vector notation as

Next we insert the expression for the

vector from Eq.

9.8-5

to get the equation of energy:

rate of increase of

energy per

unit

volume

pv)

rate of work

done on fluid per

unit volume

pressure forces

rate of energy addition rate of energy addition

per unit volume by per unit volume

convective transport heat conduction

vl)

p(v

rate of work done

on fluid per unit on fluid per unit

volume by viscous

volume by external

forces forces

This equation does not include nuclear, radiative, electromagnetic, or chemical forms of

energy. For viscoelastic fluids, the next-to-last term has to be reinterpreted by replacing

"viscous" by "viscoelastic."

Equation 11.1-7 is the main result of this section, and it provides the basis for the re-

mainder of the chapter. Th? equation can be written in another form to include the poten-

tial energy per unit mass,

which has been defined earlier by g

-V@

(see 33.3). For

moderate elevation changes, this gives

gh, where

is a coordinate in the direction

336

Chapter

The Equations of Change for Nonisothermal Systems

opposed to the gravitational field. For terrestrial problems, where the gravitational field

independent of time, we can write

p(v

(pv

v&)

.l-8)

-(V

pv6)

pv)

Use vector identity in Eq.

A.4-19

Use Eq.

3.1-4

-(V

spv9)

&3@)

Use

independent of

When this result is inserted into Eq.

11.1-7

we get

(&u2

pii

p6)

-(V

(ipv2

,06)v)

pv)

v])

(11.1-9)

Sometimes it is convenient to have the energy equation in this form.

511.2

SPECIAL

FORMS

THE ENERGY EQUATION

The most useful form of the energy equation is one in which the temperature appears.

The object of this section is to arrive at such an equation, which can be used for predic-

tion of temperature profiles.

First we subtract the mechanical energy equation in Eq.

3.3-1

from the energy equa-

tion in

11.1-7.

This leads to the following

equation of change for internal energy:

rate of net rate of rate of internal

increase in addition of energy addition

internal internal energy by heat conduction,

energy by convective per unit

per unit transport, volume

volume per unit volume

p(V v)

(T:VV)

reversible

rate

irreversible

rate

of internal

internal energy

energy increase increase per unit

per unit volume volume by

compression viscous dissipation

It is now of interest to compare the mechanical energy equation of Eq.

3.3-1

and the

in-

ternal energy equation of Eq.

11.2-1.

Note that the terms

p(V

and

(T:VV)

appear

both equations-but with opposite signs. Therefore, these terms describe the intercon-

version of mechanical and thermal energy. The term

p(V

can be either positive

negative, depending on whether the fluid is expanding or contracting; therefore it repre-

sents

reversible

mode of interchange. On the other hand, for Newtonian fluids, the

quantity

(T:VV)

is always positive (see Eq.

3.3-3)

and therefore represents an

irreversible

degradation of mechanical into internal energy. For viscoelastic fluids, discussed

Chapter

the quantity

-(T:VV)

does not have to be positive, since some energy may

stored as elastic energy.

We pointed out in

s3.5

that the equations of change can be written somewhat more

compactly by using the substantial derivative (see Table

3.5-1).

Equation

11.2-1

can