Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

s10.3

Heat Conduction with a Nuclear Heat Source

297

Rate of heat out

by conduction

qlF)l

r+Ar

4v(r

Ad2

(4dqlF')

atr

Rate of thermal

energy produced S,

-4d

by nuclear fission

Substitution of these terms into the energy balance of

Eq.

10.1-1 gives, after dividing by

4~r

and taking the limit as

Taking the limit and introducing the expression in Eq. 10.3-1 leads to

The differential equation for the heat flux

qlc'

the cladding is of the same form as

Eq.

10.3-6, except that there is no significant source term:

Integration of these two equations gives

in which

c;"

and

CjC'

are integration constants. These are evaluated by means of the

boundary conditions:

B.C.

Evaluation of the constants then leads to

These are the heat flux distributions in the fissionable sphere and in the spherical-shell

cladding.

Into these distributions we now substitute Fourier's law of heat conduction (Eq.

B.2-7):

298

Chapter

Shell Energy Balances and Temperature Distributions in Solids and Laminar Flow

These equations may be integrated for constant

Ic'~'

and

k("

to give

The integration constants can be determined from the boundary conditions

B.C.

where

is the known temperature at the outside of the cladding. The final expressions

for the temperature profiles are

ko find the maximum

temperature in the sphere of fissionable material, all we have to do is set

equal to zero

Eq.

10.3-20.

This is a quantity one might well want to know when making estimates

thermal deterioration.

This problem has illustrated two points: (i) how to handle a position-dependent

source term, and (ii) the application of the continuity of temperature and normal heat

flux at the boundary between two solid materials.

510.4

HEAT CONDUCTION WITH A VISCOUS HEAT SOURCE

Next we consider the flow of an incompressible Newtonian fluid between two coaxial

cylinders as shown in Fig.

10.4-1.

The surfaces of the inner and outer cylinders are main-

tained at

and

Tb,

respectively. We can expect that

will be a function of

alone.

Outer cylinder moves with

angular velocity

-----

Fig.

10.4-1.

Flow between cylinders with viscous

heat generation. That part of the system enclosed

within the dotted lines is shown in modified form

in Fig.

10.4-2.

g10.4 Heat Conduction with a Viscous Heat Source

299

T~~

surface

moves

with velocity

Fig.

10.4-2.

Modification of a portion

the flow

system in Fig. 10.4-1, in which the curvature of the

bounding surfaces is neglected.

~tationar$ surface

As the outer cylinder rotates, each cylindrical shell of fluid "rubs" against an adja-

cent shell of fluid. This friction between adjacent layers of the fluid produces heat; that

is, the mechanical energy is degraded into thermal energy. The volume heat source re-

sulting from this "viscous dissipation," which can be designated by

S,,

appears automat-

ically in the shell balance when we use the combined energy flux vector

defined at the

end of Chapter 9, as we shall see presently.

If the slit width

is small with respect to the radius

of the outer cylinder, then the

problem can be solved approximately by using the somewhat simplified system de-

picted in Fig. 10.4-2. That is, we ignore curvature effects and solve the problem in Carte-

sian coordinates. The velocity distribution is then v,

vb(x/b), where vb

flR.

We now make an energy balance over a shell of thickness Ax, width

and length

Since the fluid is in motion, we use the combined energy flux vector

as written in Eq.

9.8-6. The balance then reads

Dividing by

Ax and letting the shell thickness Ax go to zero then gives

This equation may be integrated to give

Since we do not know any boundary conditions for ex, we cannot evaluate the integra-

tion constant at this point.

We now insert the expression for

f;om Eq. 9.8-6. Since the velocity component in

the x direction is zero, the term (ipv2

pLnv can be discarded. The x-component of

-k(dT/dx) according to Fourier's law. The x-component of

v] is, as shown in Eq.

9.8-1,

T,,v,

~~~v~

T,,v,. Since the only nonzero component of the velocity is v, and

since

T,,

-p(dv,/dx) according to Newton's law of viscosity, the x-component of

is -pu,(dv,/dx). We conclude, then, that Eq. 10.4-3 becomes

When the linear velocity profile v,

vb(x/b) is inserted, we get

in which

p(~[,/b)~

can be identified as the rate of viscous heat production per unit volume

S,.

When

Eq.

10.4-5 is integrated we get

300

Chapter

Shell Energy Balances and Temperature Distributions in Solids and Laminar Flow

The two integration constants are determined from the boundary conditions

B.C. 1:

B.C.

This yields finally, for Tb

Here Br

pz;/k(Tb

To) is the dimensionless Brinkman number,' which is a measure

the importance of the viscous dissipation term. If Tb

To,

then

Eq.

10.4-9 can be written

and the maximum temperature is at x/b

If the temperature rise is appreciable, the temperature dependence of the viscosity

has to be taken into account. This is discussed in Problem 10C.l.

The viscous heating term S,

p(vb/b)' may be understood by the following argu-

ments. For the system in Fig. 10.4-2, the rate at which work is done is the force acting

the upper plate times the velocity with which it moves, or

(-T~=WL)(V~).

The rate of en-

ergy addition per unit volume is then obtained by dividing this quantity by

WLb,

which

gives (-7,,vb/b)

p(~~/b)~. This energy all appears as heat and is hence S,.

In most flow problems viscous heating is not important. However if there are large

velocity gradients, then it cannot be neglected. Examples of situations where viscous

heating must be accounted for include: (i) flow of a lubricant between rapidly moving

parts, (ii) flow of molten polymers through dies in high-speed extrusion, (iii) flow

highly viscous fluids in high-speed viscometers, and (iv) flow of air in the boundary

layer near an earth satellite or rocket during reentry into the earth's atmosphere.

The

first two of these are further complicated because many lubricants and molten plastics

are non-Newtonian fluids. Viscous heating for non-Newtonian fluids is illustrated in

Problem 10B.

510.5

HEAT CONDUCTION WITH

CHEMICAL HEAT SOURCE

chemical reaction is being carried out in a tubular, fixed-bed flow reactor with inner

radius

as shown in Fig. 10.5-1. The reactor extends from

and is di-

vided into three zones:

Zone

Entrance zone packed with noncatalytic spheres

Zone 11: Reaction zone packed with catalyst spheres, extending from

Zone 111: Exit zone packed with noncatalytic spheres

It is assumed that the fluid proceeds through the reactor tube in "plug flowM-that is,

with axial velocity uniform at a superficial value

w/m-~~~ (see text below

Eq.

6.4-1

for the definition of "superficial velocity"). The density, mass flow rate, and superficial

Brinkman,

Appl.

Sci. Research,

A2,120-124 (1951), solved the viscous dissipation heating

problem for the Poiseuille flow in a circular tube. Other dimensionless groups that may be used for

characterizing viscous heating have been summarized

Bird,

Armstrong, and

Hassager,

Dynamics

Polymeric Liquids,

Vol.

1,2nd edition, Wiley, New York (1987), pp. 207-208.

910.5

Heat Conduction with a Chemical Heat Source

301

Insulated Inert Catalyst Inert

wall

particles particles

qAzr

particles

Zone

Zone I1

Zone I11

--+

z=L

Fig.

10.5-1.

Fixed-bed axial-flow reactor. Reactants enter at

and leave at

The reaction zone extends

from

velocity are all treated as independent of

and z. In addition, the reactor wall is assumed

to be well insulated, so that the temperature can be considered essentially independent

It is desired to find the steady-state axial temperature distribution T(z) when the

fluid enters at

-03

with a uniform temperature TI.

When a chemical reaction occurs, thermal energy is produced or consumed when

the reactant molecules rearrange to form the products. The volume rate of thermal en-

ergy production by chemical reaction,

s,,

is in general a complicated function of pres-

sure, temperature, composition, and catalyst activity. For simplicity, we represent S,

here as a function of temperature only: S,

SclF(Q), where Q

To)/(Tl

To). Here

is the local temperature in the catalyst bed (assumed equal for catalyst and fluid), and

S,, and

are empirical constants for the given reactor inlet conditions.

For the shell balance we select a disk of radius

and thickness

in the catalyst

zone (see Fig. 10.5-I), and we choose

to be much larger than the catalyst particle di-

mensions. In setting up the energy balance, we use the combined energy flux vector

inas-

much as we are dealing with a flow system. Then, at steady state, the energy balance is

Next we divide by

rR2

and take the limit as

goes to zero. Strictly speaking, this op-

eration is not "legal," since we are not dealing with a continuum but rather with a gran-

ular structure. Nevertheless, we perform this limiting process with the understanding

that the resulting equation describes, not point values, but rather average values of

and

for reactor cross sections of constant z. This gives

Now we substitute the z-component of Eq. 9.8-6 into this equation to get

We now use Fourier's law for

q,,

Eq. 1.2-6 for

r,,,

and the enthalpy expression in Eq. 9.8-8

(with the assumption that the heat capacity is constant) to get

in which the effective thermal conductivity in the

direction

K,~~,~~

has been used (see Eq.

9.6-9). The first, fourth and fifth terms on the left side may be discarded, since the veloc-

ity is not changing with z. The third term may be discarded if the pressure does not

302

Chapter 10

Shell Energy Balances and Temperature Distributions in Solids and Laminar Flow

change significantly in the axial direction. Then in the second term we replace

by the

superficial velocity

v,,

because the latter is the effective fluid velocity in the reactor.

Then

Eq. 10.5-4 becomes

This is the differential equation for the temperature in zone 11. The same equation

ap-

plies in zones I and I11 with the source term set equal to zero. The differential equations

for the temperature are then

Zone I

Zone I1

Zone I11

Here we have assumed that we can use the same value of the effective thermal conduc-

tivity in all three zones. These three second-order differential equations are subject to

the

following six boundary conditions:

B.C. 1:

atz=--03, T1=T1

B.C. 2:

at z

TII

B.C. 3:

B.C.

at z

~11

~"1

(10.5-12)

B.C. 5:

atz

dTn

d T"'

Keff,zz

B.C.

atz

TI"

finite (10.5-14)

Equations 10.5-10 to 13 express the continuity of temperature and heat flux at the bound-

aries between the zones. Equations 10.5-9 and

specify requirements at the two ends

the system.

The solution of Eqs. 10.5-6 to 14 is considered here for arbitrary F(O). In many cases

of practical interest, the convective heat transport is far more important than the axial

conductive heat transport. Therefore, here we drop the conductive terms entirely (those

containing K,~~,~~). This treatment of the problem still contains the salient features of

the

solution in the limit of large

RePr (see Problem 10B.18 for a fuller treatment).

If we introduce a dimensio_nless axial coordinate Z

z/L

and a dimensionless

chemical heat source

ScIL/pC,~ti(Tl

TO), then Eqs. 10.5-6 to 8 become

Zone I

dO1

(10.5-15)

Zone

(o<z<I)

d@I1

j,gqO)

(10.5-16)

d@III

Zone I11 (Z>1)

-- -

0 (10.5-17)

for which we need three boundary conditions:

B.C.

B.C. 2:

B.C. 3:

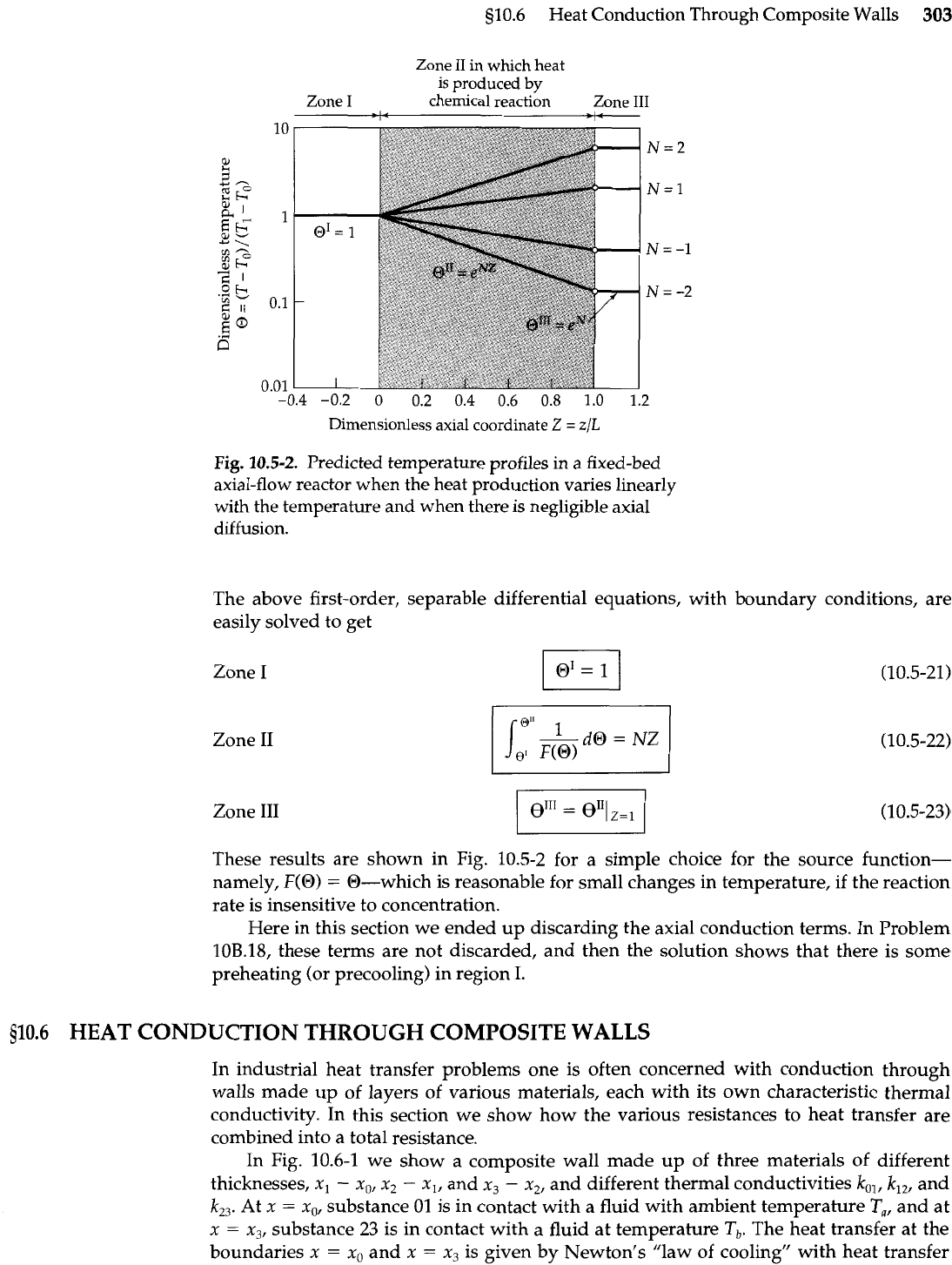
1.6

Heat Conduction Through Composite Walls

303

Zone

in which heat

is produced

Zone

chemical reaction Zone

I11

Dimensionless axial coordinate

z/L

Fig.

10.5-2.

Predicted temperature profiles in

fixed-bed

axial-flow

reactor when the heat production varies linearly

with the temperature and when there is negligible axial

diffusion.

The above first-order, separable differential equations, with boundary conditions, are

easily solved to get

Zone

I11

These results are shown in Fig. 10.5-2 for a simple choice for the source function-

namely,

F(0)

@-which is reasonable for small changes in temperature, if the reaction

rate is insensitive to concentration.

Here in this section we ended up discarding the axial conduction terms. In Problem

10B.18, these terms are not discarded, and then the solution shows that there is some

preheating (or precooling) in region

510.6

HEAT CONDUCTION THROUGH COMPOSITE

WALLS

industrial heat transfer problems one is often concerned with conduction through

walls made up of layers of various materials, each with its own characteristic thermal

conductivity.

this section we show how the various resistances to heat transfer are

combined into

total resistance.

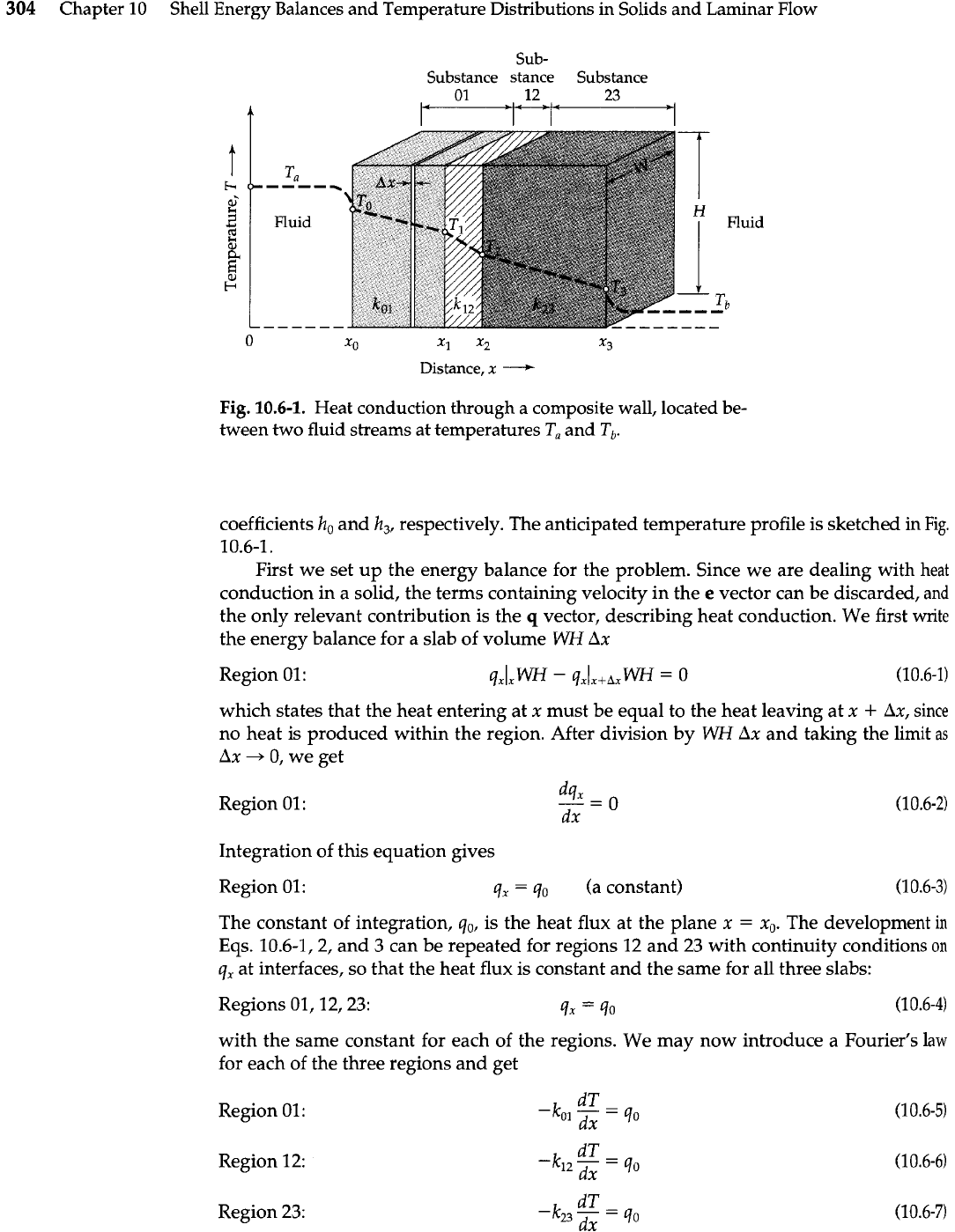
In Fig. 10.6-1 we show

composite wall made up of three materials of different

thicknesses, x,

x,, x,

x,, and x,

x,, and different thermal conductivities

k,,,

and

k2,.

At x

x,, substance

is in contact with a fluid with ambient temperature

T,,

and at

x,, substance

is in contact with a fluid at temperature

Tb.

The heat transfer at the

boundaries x

xo and

is given by Newton's "law of cooling" with heat transfer

304

Chapter 10 Shell Energy Balances and Temperature Distributions in Solids and Laminar Flow

Sub-

Substance stance Substance

Fluid

------

Distance,

--+

Fig.

10.6-1.

Heat conduction through a composite wall, located be-

tween two fluid streams at temperatures

and

Tb.

coefficients

and h3, respectively. The anticipated temperature profile is sketched in Fig.

10.6-1.

First we set up the energy balance for the problem. Since we are dealing with

heat

conduction in a solid, the terms containing velocity in the

vector can be discarded,

and

the only relevant contribution is the

vector, describing heat conduction. We first

write

the energy balance for a slab of volume

Region 01

~x~xW

qxlx+~x~

0 (10.6-1)

which states that the heat entering at x must be equal to the heat leaving at x

Ax, since

no heat is produced within the region. After division by

Ax and taking the limit

we get

Region 01

dqx

0 (10.6-2)

Integration of this equation gives

Region 01

q, (a constant) (1 0.6-3)

The constant of integration,

qo,

the heat flux at the plane x

xo. The development

Eqs. 10.6-1,2, and 3 can be repeated for regions 12 and 23 with continuity conditions

at interfaces, so that the heat flux is constant and the same for all three slabs:

Regions 01,12,23:

40 (10.6-4)

with the same constant for each of the regions. We may now introduce a Fourier's

law

for each of the three regions and get

Region 01:

Region 12:

Region 23:

g10.6

Heat Conduction Through Composite Walls

305

We now assume that

k,,,

k,,, and

k2,

are constants. Then we integrate each equation over

the entire thickness of the relevant slab of material to get

Region

01:

Region

12:

Region 23:

In addition we have the two statements regarding the heat transfer at the surfaces ac-

cording to Newton's law of cooling:

At surface

At surface 3:

Addition of these last five equations then gives

Sometimes this result is rewritten in a form reminiscent of Newton's law of cooling, ei-

ther in terms of the heat flux

(J/m2 s) or the heat flow Q, U/s):

The quantity U, called the "overall heat transfer coefficient," is given then by the follow-

ing famous formula for the "additivity of resistances":

Here we have generalized the formula to a system with

slabs of material. Equations

10.6-15

and 16 are useful for calculating the heat transfer rate through a composite wall

separating two fluid streams, when the heat transfer coefficients and thermal conductivi-

ties are known. The estimation of heat transfer coefficients is discussed in Chapter

14.

In the above development it has been tacitly assumed that the solid slabs are con-

tiguous with no intervening "air spaces." If the solid surfaces touch each other only at

several points, the resistance to heat transfer will be appreciably increased.

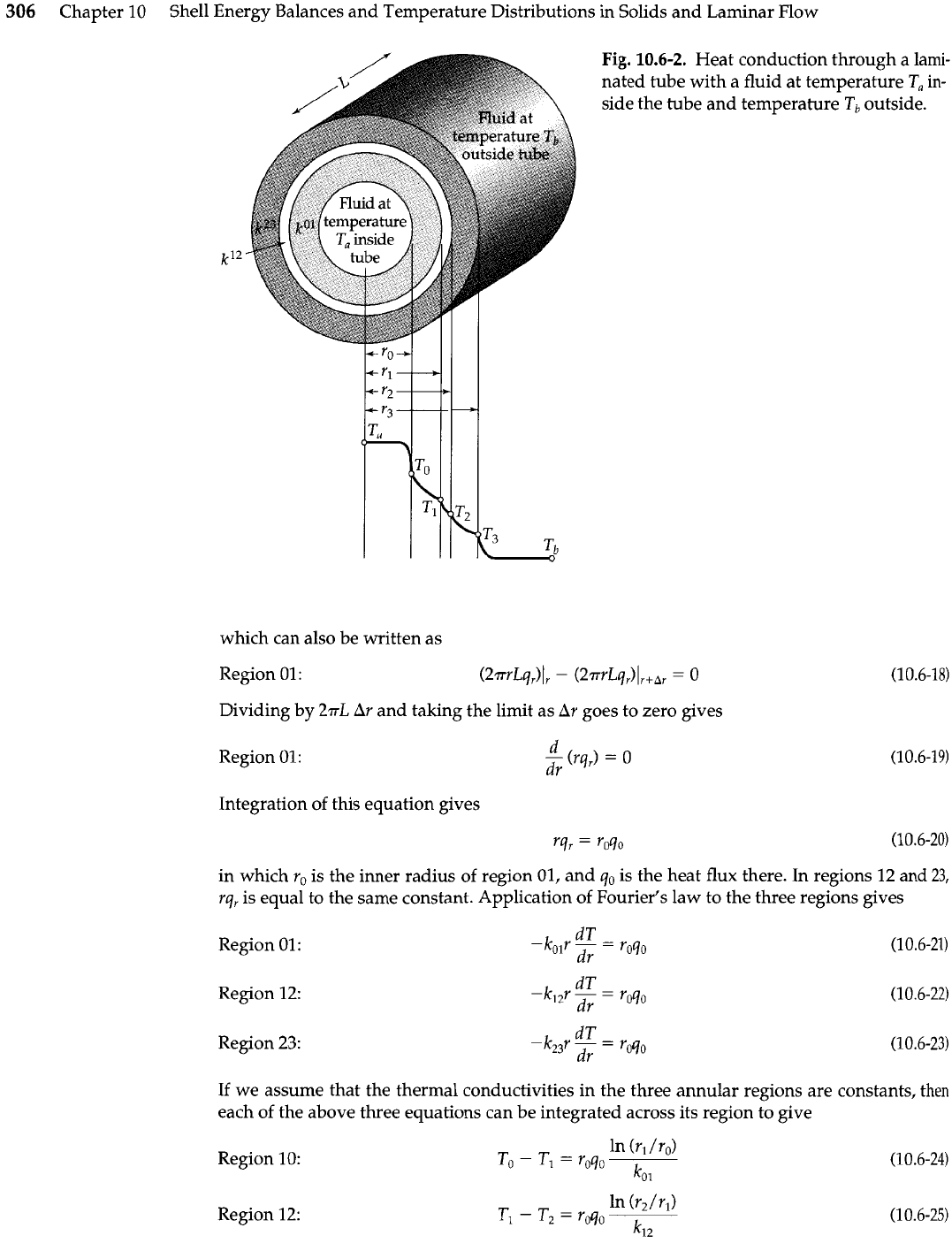
Develop a formula for the overall heat transfer coefficient for the composite cylindrical pipe

wall shown in Fig.

10.6-2.

Composite Cylindrical

Walls

SOLUTION

An energy balance on a shell of volume

2m-L Ar

for region

Region

01:

q,l,

2mL

q,l,+A,.

2r(r

Ar)L

306

Chapter

Shell Energy Balances and Temperature Distributions in Solids and Laminar Flow

which can also be written as

Region

01:

Fig.

10.6-2.

Heat conduction through a lami-

nated tube with a fluid at temperature

in-

side the tube and temperature

outside.

Dividing by

2.rrL

and taking the limit as

goes to zero gives

Region

01:

('4,)

0 (10.6-19)

Integration of this equation gives

in which

is the inner radius of region

01,

and

is the heat flux there. In regions

and

23,

rq,

is equal to the same constant. Application of Fourier's law to the three regions gives

Region

01:

-kolr

r,q, (10.6-21)

Region

12:

k,,r

r,qo

(10.6-22)

Region

23:

k23~

TogD

(10.6-23)

If we assume that the thermal conductivities in the three annular regions are constants,

then

each of the above three equations can be integrated across its region to give

Region

10:

Region

12: