Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

s9.3

Theory of Thermal Conductivity of Gases at Low Density

277

Table

9.3-1

Predicted and Observed Values of the Prandtl Number for Gases

at Atmospheric Pressurea

&~/k

from

ePr

from observed

Gas T(K)

Eq.

9.3-16 values of

C,,

p, and

Air

Calculated from values given

Jakob,

Heaf Transfer,

Wiley,

New York (19491,

pp.

75-76.

Hirschfelder,

C. F.

Curtis, and

Bird,

Molecular Theory

Gases and Liquids,

Wiley,

New York, corrected printing (1964),

16.

(see

Eq.

1.4-16).

All

values of

Eq.

9.3-17 and

Eq.

1.4-16 are low-density values

at the give; temperature.

viscosity data are not available, they may be estimated

from

and

via

Eq.

9.3-15. Comparisons with experimental data7 indicate an average

deviation of about

for mixtures containing nonpolar polyatomic gases, including

02,

N2,

CO,

C2H2, and CH,.

Compute the thermal conductivity of Ne at

atm and 373.2K.

Computation

the

SOLUTION

lhenal

Conductivity

From Table E.l the Lennard-Jones constants for neon are

2.789

and

E/K

35.7K, and

'fa

Monatomic

Gas

its molecular weight

is 20.183. Then, at 373.2K,

have KT/E

373.2/35.7

10.45. From

Low

Density

Table E.2 we find that

flk

fl,

0.821. Substitution into Eq. 9.3-13 gives

measured value of 1.35

cal/cm. s

has been reported8 at 1 atm and 373.2K.

Kannuluik and

Carman,

Proc. Phys. Soc.

(London),

65B,

701-704 (1952).

278

Chapter 9 Thermal Conductivity and the Mechanisms of Energy Transport

Estimation of the

Thermal Conductivity

of a Polyatomic Gas

at Low Density

EXAMPLE

9.3-3

Prediction of the

Thermal

Conductivity

a Gas Mixture at

Low Density

Estimate the thermal conductivity of molecular oxygen at 300K and low pressure.

SOLUTION

The molecular weight of

is 32.0000; its molar heat capacity

at 300°K and low pressure

7.019 cal/g-mole

From Table E.l we find the Lennard-Jones parameters for molecular

oxygen to be

3.433

and

E/K

113K. At 300K, then,

KT/E

300/113

2.655. From

Table E.2, we find

1.074. The viscosity, from Eq. 1.4-14, is

Then, from Eq. 9.3-15, the Eucken approximation to the thermal conductivity is

This compares favorably with the experimental value of 0.02657 W/m

in Table 9.1-2.

Predict the thermal conductivity of the following gas mixture at 1 atm and 293K from the

given data on the pure components at the same pressure and temperature:

Mole Molecular

fraction weight

lo7

Species

(g/cm. s)

(cal/cm

SOLUTION

Use Eq. 9.3-17. We note that the for this gas mixture at these conditions have already

been

computed in the viscosity calculation in Example 1.4-2. In that example we evaluated the fol-

lowing summations, which also appear in

Eq.

9.3-17:

Substitution in

Eq.

9.3-17 gives

data are available for comparison at these conditions.

59.4

Theory of Thermal Conductivity of Liquids

279

59.4

THEORY OF THERMAL CONDUCTIVITY OF LIQUIDS

very detailed kinetic theory for the thermal conductivity of monatomic liquids was

developed a half-century ago,' but it has not yet been possible to implement it for prac-

tical calculations. As a result we have to use rough theories or empirical estimation

methods.'

We choose to discuss here Bridgman's simple theory3 of energy transport in pure

liquids. He assumed that the molecules are arranged in a cubic lattice, with a center-

to-center spacing given by in which

?/N

is the volume per molecule. He

further assumed energy to be transferred from one lattice plane to the next at the

sonic velocity

for the given fluid. The development is based on a reinterpretation of

Eq. 9.3-11 of the rigid-sphere gas theory:

The heat capacity at constant volume of a monatomic liquid is about the scme as for a

solid at high temperature, which is given by the Dulong and Petit formula4

3(~/m).

The mean molecular speed in the

direction,

is replaced by the sonic velocity

us.

The

distance a that the energy travels between two successive collisions is taken to be the lat-

tice spacing

(?/I?)'13.

Making these substitutions in Eq. 9.4-1 gives

which is Bridgrnan's equation. Experimental data show good agreement with Eq. 9.4-2,

even for polyatomic liquids, but the numerical coefficient is somewhat too high. Better

agreement is obtained if the coefficient is changed to

2.80:

This equation is limited to densities well above the critical density, because of the tacit

assumption that each molecule oscillates in a "cage" formed by its nearest neighbors.

The success of this equation for polyatomic fluids seems to imply that the energy trans-

fer

collisions of polyatomic molecules is incomplete, since the heat capacity used here,

3(~/rn), is less than the heat capacities of polyatomic liquids.

The

velocity of low-frequency sound is given (see Problem 11C.1) by

The quantity (dp/dp), may be obtained from isothermal compressibility measurements

or from an equation of state, and (Cp/Cv) is very nearly unity for liquids, except near the

critical point.

Irving and

G. Kirkwood,

Chem. Phys.,

18,817-829

(1950).

This theory has been extended

to polymeric liquids by

Curtiss and R. B. Bird,

Chem. Phys.,

107,5254-5267 (1997).

Reid,

M. Prausnitz, and

Poling,

The Properties of Gases and

Liquids,

McGraw-Hill,

New York

(1987);

Riedel,

Chemie-1ng.-Techn.,

27,209-213

(1955).

Bridgman,

Proc. Am. Acad. Arts and Sci.,

59,141-169 (1923).

Bridgman's equation is often

misquoted, because he gave it in terms of a little-known gas constant equal to

SK.

This empirical equation has been justified, and extended, by

Einstein

[Ann. Phys.

[41,22,

180-190 (1907)l

and

Debye

[Ann.

Phys.,

[4139,789-839 (1912)l.

Equation

9.4-3

is in approximate agreement with a formula derived by

Powell,

Roseveare, and

Eyring,

Ind. Eng. Chem.,

33,430-435

(1941).

280

Chapter 9

Thermal Conductivity and the Mechanisms of Energy Transport

EXAMPLE

9.4-1

Prediction

the

The density of liquid CCI, at

20°C

and 1 atm is 1.595 g/cm3, and its isothermal compressibility

(l/p)(ap/a~)~ is 90.7

atm-'. What is its thermal conductivity?

Thermal Conductivity

SOLUTION

of a Liquid

First compute

7.00

lo9

cm2/s2 (using Appendix

(9.4-5)

Assuming that

CJC,

1.0,

get from

Eq.

9.4-4

The molar volume is

M/p

153.84/1.595

96.5 cm3/g-mole. Substitution of these val-

ues in Eq. 9.4-3 gives

The experimental value as interpolated from Table 9.1-3 is 0.101 W/m

s9.5

THERMAL CONDUCTIVITY OF SOLIDS

Thermal conductivities of solids have to be measured experimentally, since they depend

on many factors that are difficult to measure or predict.' In crystalline materials, the

phase and crystallite size are important; in amorphous solids the degree of molecular

orientation has a considerable effect. In porous solids, the thermal conductivity is

strongly dependent on the void fraction, the pore size, and the fluid contained in the

pores.

detailed discussion of thermal conductivity of solids has been given by Jakob.'

In general, metals are better heat conductors than nonmetals, and crystalline materi-

als conduct heat more readily than amorphous materials.

Dry

porous solids are very

poor heat conductors and are therefore excellent for thermal insulation. The conductivi-

ties of most pure metals decrease with increasing temperature, whereas the conductivi-

ties of nonmetals increase; alloys show intermediate behavior. Perhaps the most useful

of the rules of thumb is that thermal and electrical conductivity go hand in hand.

For pure metals, as opposed to alloys, the thermal conductivity

and the electrical

conductivity

are related approximately3 as follows:

constant

This is the

Wiedemann-Franz-Lorenz equation;

this equation can also be explained theoret-

ically (see Problem

9A.6).

The "Lorenz number"

is about

lop9

volt2/K2 for

Goldsmith,

Waterman, and H. J. Hirschhorn, eds.,

Handbook of Thermophysical Properfies of

Solids,

Macmillan, New York (1961).

Jakob,

Heat Transfer,

Vol. 1, Wiley, New York (1949), Chapter

See also

Rohsenow,

Hartnett, and Y.

Cho, eds., Handbook of

Heat

Transfer,

McGraw-Hill, New York (1998).

Wiedemann and

Franz,

Ann. Phys.

Chernie,

89,497-531

(1853);

Lorenz,

Poggendorff's

Annalen,

147,429-452

(1872).

s9.6

Effective Thermal Conductivity of Composite Solids

281

pure metals at 0°C and changes but little with temperatures above O°C, increases of

10-20% per 1000°C being typical. At very low temperatures (-269.4"C for mercury) met-

als become superconductors of electricity but not of heat, and

thus varies strongly with

temperature near the superconducting region. Equation 9.5-1 is of limited use for alloys,

since

varies strongly with composition and, in some cases, with temperature.

The success of

Eq.

9.5-1 for pure metals is due to the fact that free electrons are the

major heat carriers in pure metals. The equation is not suitable for nonmetals, in which

the concentration of free electrons is so low that energy transport by molecular motion

predominates.

59.6

EFFECTIVE THERMAL CONDUCTIVITY

COMPOSITE SOLIDS

Up to this point we have discussed homogeneous materials. Now we turn our attention

briefly to the thermal conductivity of two-phase solids--one solid phase dispersed in a

second solid phase, or solids containing pores, such as granular materials, sintered met-

als, and plastic foams. A complete description of the heat transport through such materi-

als is clearly extremely complicated. However, for steady conduction these materials can

be regarded as homogeneous materials with an

effective thermal conductivity

keff,

and the

temperature and heat flux components are reinterpreted as the analogous quantities av-

eraged over a volume that is large with respect to the scale of the heterogeneity but small

with respect to the overall dimensions of the heat conduction system.

The first major contribution to the estimation of the conductivity of heterogeneous

solids was by Maxwell.' He considered a material made of spheres of thermal conductiv-

ity

embedded in a continuous solid phase with thermal conductivity

ko.

The volume

fraction

of embedded spheres is taken to be sufficiently small that the spheres do not

"interact" thermally; that is, one needs to consider only the thermal conduction in a large

medium containing only one embedded sphere. Then by means of a surprisingly simple

derivation, Maxwell showed that for

small volume fraction

(see Problems llB.8 and llC.5).

For

large volume fraction

Rayleigh2 showed that, if the spheres are located at the

in-

tersections of a cubic lattice, the thermal conductivity of the composite is given by

Comparison of this result with

Eq.

9.6-1 shows that the interaction between the spheres

is small, even at

in,

the maximum possible value of

for the cubic lattice arrange-

ment. Therefore the simpler result of Maxwell is often used, and the effects of nonuni-

form sphere distribution are usually neglected.

Maxwell's derivation was for electrical conductivity, but

the

same arguments apply for thermal

conductivity. See J.

Maxwell,

Treatise on Electricity and Magnetism,

Oxford University Press, 3rd

edition (1891, reprinted 1998), Vol. 1,

s314;

S. Carslaw and

Jaeger,

Conduction

Heat in Solids,

Clarendon Press, Oxford, 2nd edition (1959),

428.

Strutt (Lord Rayleigh),

Phil.

Mag.

(5),

34,431-502 (1892).

282

Chapter

Thermal Conductivity and the Mechanisms of Energy Transport

For nonspherical inclusions, however,

Eq.

9.6-1 does require modification. Thus for

square arrays of long cylinders parallel to the

axis, ~aylei~h~ showed that the

com-

ponent of the thermal conductivity tensor

and the other two components are

Keff,

(9.6-4)

(0.305844~

0.0133634~

. .

-1

That is,

the composite solid containing aligned embedded cylinders is anisotropic. The effective

thermal conductivity tensor has been computed up to

0(+')

for a medium containing

spheroidal

inclusion^.^

For complex nonspherical inclusions, often encountered in practice, no exact treatment

is possible, but some approximate relations are a~ailable.~,~,~ For simple unconsolidated

granular beds the following expression has proven successful:

which

The

are "shape factors" for the granules of the medium: and they must satisfy g,

For spheres g1

and

Eq.

9.6-5 reduces to

Eq.

9.6-1. For unconsol-

idated soils? gl

and g3

The structure of consolidated porous beds-for ex-

ample, sandstones-is considerably more complex.

Some success is claimed for

predicting the effective conductivity of such s~bstances;l.~,~ but the generality of the

methods is not yet known.

For solids containing gas

pocket^,^

thermal radiation (see Chapter 16) may be impor-

tant. The special case

parallel planar fissures perpendicular to the direction of heat

conduction is particularly important for high-temperature insulation. For such systems

may be shown that

where

is the Stefan-Boltzmann constant,

is the thermal conductivity of the gas, and

is the total thickness of the material in the direction of the heat conduction.

modifica-

tion of this equation for fissures of other shapes and orientations is a~ailable.~

S.-Y.

and

Kim,

AIChE lournal,

36,927-938 (1990).

Odelevskii,

Tech. Phys.

(USSR), 24,667

and

697 (1954);

Euler,

Appl. Phys.,

28,1342-1346

(1957).

de Vries,

Mededelingen van de Landbouwhogeschool te Wageningen,

(1952);

see also

Ref.

and

D. A.

de Vries, Chapter

Physics

Plant Environment,

van Wijk, ed., Wiley,

New

York

(1963).

W. Woodside and

Messmer,

Appl. Phys.,

32,1688-1699,1699-1706 (1961).

Loeb,

Amer. Ceramic Soc.,

37,96-99 (1954).

Sh.

Plyat,

Soviet Physics

JETP,

2,2588-2589 (1957).

M. Jakob,

Heat Transfer,

Wiley,

New

York

(1959),

Vol.

1,§6.5.

59.7

Convective Transport of Energy

283

For

gas-filled granular

beds6r9

a different type of complication arises. Since the thermal

conductivities of gases are much lower than those of solids, most of the gas-phase heat

conduction is concentrated near the points of contact of adjacent solid particles. As a re-

sult, the distances over which the heat is conducted through the gas may approach the

mean free path of the gas molecules. When this is true, the conditions for the develop-

ments of 59.3 are violated, and the thermal conductivity of the gas decreases. Very effec-

tive insulators can thus be prepared from partially evacuated beds of fine powders.

Cylindrical ducts filled with granular materials through which a fluid

flowing

(in

the

di-

rection) are of considerable importance in separation processes and chemical reactors. In

such systems the effective thermal conductivities in the radial and axial directions are

quite different and are designated1' by

K~~~,~~

and

K,,,,,.

Conduction, convection, and radia-

tion all contribute to the flow of heat through the porous medium." For highly turbulent

flow, the energy is transported primarily

the tortuous flow of the fluid in the inter-

stices of the granular material; this gives rise to a highly anisotropic thermal conductivity.

For a bed of uniform spheres, the radial and axial components are approximately

in which vo is the "superficial velocity" defined in 54.3 and 56.4, and

is the diameter of

the spherical particles. These simplified relations hold for Re

D,vop/p greater than

200.

The behavior at lower Reynolds numbers is discussed in several references.12 Also,

the behavior of the effective thermal conductivity tensor as a function of the Pkclet num-

ber has been studied in considerable detail.13

59.7

CONVECTIVE

TRANSPORT OF

ENERGY

In 59.1 we gave Fourier's law of heat conduction, which accounts for the energy trans-

ported through a medium by virtue of the molecular motions.

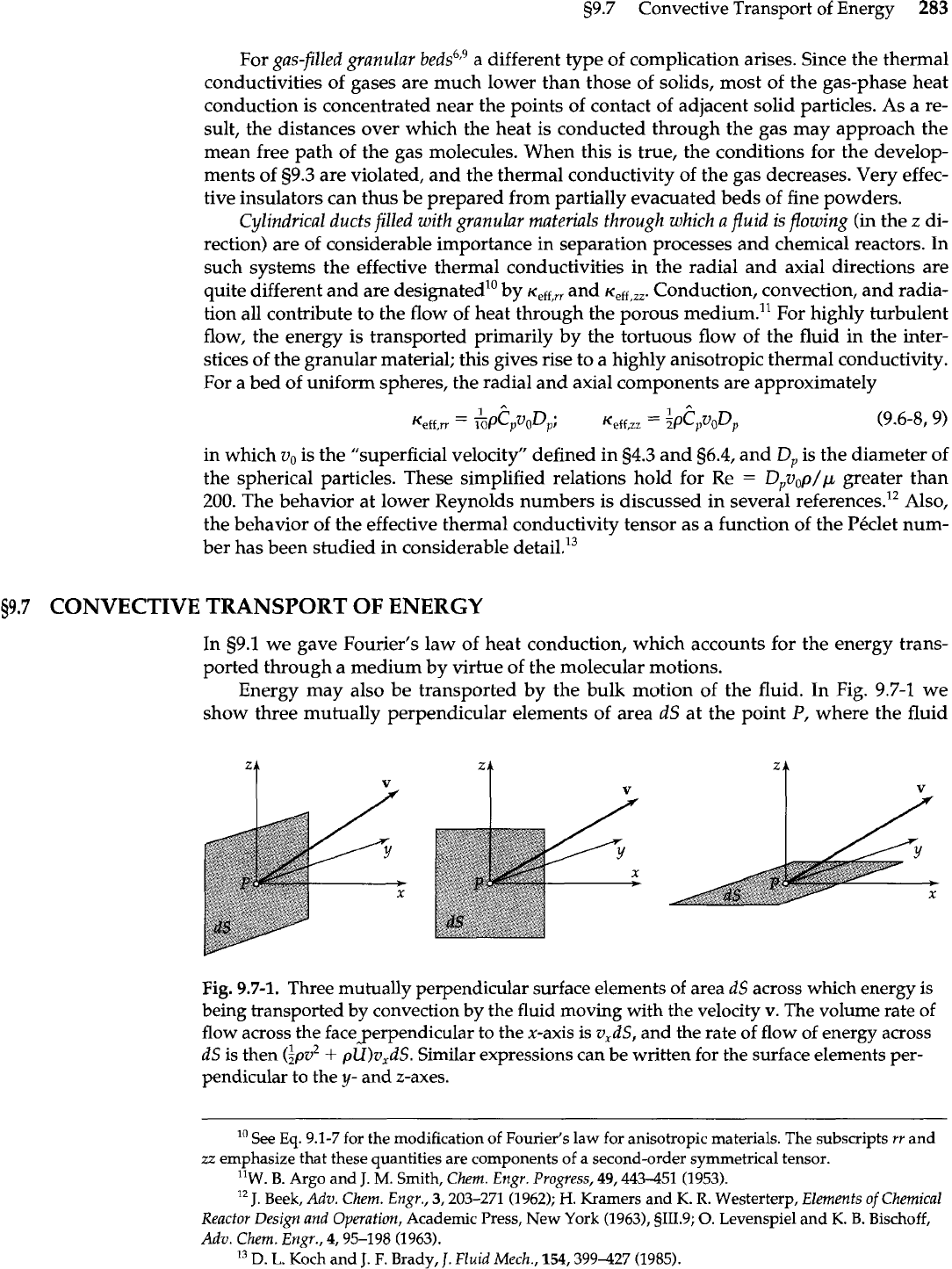
Energy may also be transported by the bulk motion of the fluid. In Fig. 9.7-1 we

show three mutually perpendicular elements of area

at the point

where the fluid

Fig.

9.7-1.

Three mutually perpendicular surface elements of area dS across which energy is

being transported by convection by the fluid moving with the velocity

The

volume rate of

flow across the faceperpendicular to the x-axis is v,dS, and the rate of flow of energy across

is then

(ipv2

pU)v,dS. Similar expressions can be written for the surface elements per-

pendicular to the

and z-axes.

See

Eq.

9.1-7

for the modification of Fourier's law for anisotropic materials. The subscripts

and

emphasize that these quantities are components of a second-order symmetrical tensor.

"W. B. Argo and

Smith,

Chem. Engr. Progress,

49,443-451 (1953).

Beek,

Adv. Chem. Engr.,

3,203-271 (1962);

Kramers and

Westerterp,

Elements

Chemical

Reacfor Design and Operation,

Academic Press, New York

(1963), gIII.9;

Levenspiel and

B. Bischoff,

Adv. Chem. Engr.,

4,95-198 (1963).

Koch

and

Brady,

Fluid Mech.,

154,399427 (1985).

284

Chapter

Thermal Conductivity and the Mechanisms of Energy Transport

velocity is v. The volume rate of flow across the surface element dS perpendicular to the

x-axis is v,dS. The rate at which energy is being swept across the same surface element is

then

in which $pv2

$p(v:

vi)

is the kinetic energy per unit volume, and pir is the inter-

nal energy per unit volume.

The definition of the internal energy in a nonequilibrium situation requires some

care. From the continuum point of view, the internal energy at position r and time t is as-

sumed to be the same function of the local, instantaneous density and temperature that

one would have at equilibrium. From the molecular point of view, the internal energy

consists of the sum of the kinetic energies of all the constituent atoms (relative to the

flow velocity v), the intramolecular potential energies, and the intermolecular energies,

within a small region about the point

at time t.

Recall that, in the discussion of molecular collisions in 50.3, we found it convenient

to regard the energy of a colliding pair of molecules to be the sum of the kinetic energies

referred to the center of mass of the molecule plus the intramolecular potential energy

the molecule. Here also we split the energy of the fluid (regarded as a continuum) into

kinetic energy associated with the bulk fluid motion and the internal energy associated

with the kinetic energy of the molecules with respect to the flow velocity and the intra-

and intermolecular potential energies.

We can write expressions similar to Eq. 9.7-1 for the rate at which energy is being

swept through the surface elements perpendicular to the

and z-axes. If we now multi-

ply each of the three expressions by the corresponding unit vector and add, we then get,

after division by dS,

and this quantity is called the convective energy flux vector. To get the convective energy

flux across a_ unit surface whose normal unit vector is

we form the dot product

($v2

pU)v). It is understood that this is the flux from the negative side of the sur-

face to the positive side. Compare this with the convective momentum flux in Fig. 1.7-2.

g9.8

WORK ASSOCIATED

WITH

MOLECULAR MOTIONS

Presently we will be concerned with applying the law of conservation of energy to

"shells" (as in the shell balances in Chapter 10) or to small elements of volume fixed

space (to develop the equation of change for energy in §11.1). The law of conservation

energy for an open flow system is an extension of the first law of classical thermodynam-

ics (for a closed system at rest). In the latter we state that the change in internal energy is

equal to the amount of heat added to the system plus the amount of work done on the

system. For flow systems we shall need to account for the heat added to the system (by

molecular motions and by bulk fluid motion) and also for the work done on the system

by the molecular motions. Therefore it is appropriate that we develop here the expres-

sion for the rate of work done by the molecular motions.

First we recall that, when a force F acts on a body and causes it to move through a

distance dr, the work done is dW

(F dr). Then the rate of doing work is dW/dt

drldt)

v)-that is, the dot product of the force times the velocity. We now

apply this formula to the three perpendicular planes at a point

in space shown

Fig.

9.8-1.

First we consider the surface element perpendicular to the x-axis. The fluid on the

minus side of the surface exerts a force

IT#

on the fluid that is on the plus side (see

g9.8

Work Associated with Molecular Motions

285

Fig.

9.8-1.

Three mutually perpendicular surface elements of area dS at point

along with

the stress vectors

m,, my,

acting on these surfaces. In the first figure, the rate at which

work is done

the

fluid

on the minus side of dS on the fluid on the plus side of

is then

(a,.

v)dS

v],dS. Similar expressions hold for the surface elements perpendicular to

the other two coordinate axes.

Table 1.2-1). Since the fluid is moving with a velocity v, the rate at which work is done

by the minus fluid on the plus fluid is

(n,

v)dS. Similar expressions may be written for

the work done across the other two surface elements. When written out in component

form, these rate of work expressions, per unit area, become

When these scalar components are multiplied by the unit vectors and added, we get the

"rate of doing work vector per unit area," and we can call this, for short, the work flux:

Furthermore, the rate of doing work across a unit area of surface with orientation given

by the unit vector n is (n

v]).

Equations 9.8-1 to 9.8-4 are easily written for cylindrical coordinates by replacing

and, for spherical coordinates by replacing x,

We now define, for later use, the combined energy flux vector

as follows:

The

vector is the sum of (a) the convective energy flux,

(b)

the rate of doing work (per

unit area) by molecular mechanisms, and (c) the rate of transporting heat (per unit area)

by molecular mechanisms. All the terms in

Eq.

9.8-5 have the same sign convention, so

that

is the energy transport

the positive

direction per unit area per unit time.

The total molecular stress tensor

.rr

can now be split into two parts:

so that

v]. The term

can then be combined with !he internal

energy term to give an enthalpy term pUv

p(~

(p/p))v

p(U

pi3v

&v, so that

($pv2

pkv

(9.8-6)

We shall usually use the

vector in this form. For a surface element dS of orientation n,

the quantity (n

gives the convective energy flux, the heat flux, and the work flux

across the surface element dS from the negative side to the positive side of dS.

286

Chapter 9

Thermal Conductivity and the Mechanisms of Energy Transport

Table

9.8-1

Summary of Notation for Energy Fluxes

Symbol Meaning Reference

(ipv2

pinv convective energy flux vector Eq. 9.7-2

molecular heat flux vector Eq. 9.1-6

molecular work flux vector Eq. 9.8-4

(ipv2

pkv

combined energy flux vector

Eq. 9.8-5,6

(ipv2

pkv

In Table 9.8-1 we summarize the notation for the various energy flux vectors intro-

duced in this section. All of them have the same sign convention.

To evaluate the enthalpy in

Eq.

9.8-6,

we make use of the standard equilibrium ther-

modynamics formula

($),

(z;)~

dH=

dT+

dp=C,dT+ V-T

(:P))p

When this is integrated from some reference state pol To to the state p, TI we then get1

in which H" is the enthalpy per unit mass at the reference state. The integral over

zero for a? ideal gas and (l/p)(p

pO)

for fluids of constant density. The integral over

becomes C,(T

To) if the heat capacity can be regarded as constant over the relevant

temperature range. It is assumed that

Eq.

9.8-7 is valid in nonequilibrium systems,

where p and Tare the

local

values of the pressure and temperature.

QUESTIONS FOR DISCUSSION

Define and give the dimensions of thermal conductivity

thermal diffusivity

heat capacity

C,,

heat flux q, and combined energy flux

For the dimensions use

mass,

length,

temperature, and

time.

Compare the orders of magnitude of the thermal conductivities of gases, liquids, and solids.

In what way are Newton's law of viscosity and Fourier's law of heat conduction similar? Dis-

similar?

Are gas viscosities and thermal conductivities related? If so, how?

Compare the temperature dependence of the thermal conductivities of gases, liquids, and

solids.

Compare the orders of magnitudes of Prandtl numbers for gases and liquids.

Are the thermal conductivities of gaseous Ne20 and Ne22 the same?

Is the relation

true only for ideal gases, or is it also true for liquids? If it is not

true for liquids, what formula should be used?

What is the kinetic energy flux in the axial direction for the laminar Poiseuille flow of a New-

tonian liquid in a circular tube?

10.

What is

vl for Poiseuille flow?

See, for example,

Silbey and

Alberty,

Physical

Chemistry,

Wiley, 3rd edition

(2001), s2.11.