Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


Problems
287
PROBLEMS
9A.1
Prediction of thermal conductivities of gases at
low
density.
(a)
Compute the thermal conductivity of argon at
100°C
and atmospheric pressure, using the Chapman-Enskog
theory and the Lennard-Jones constants derived from vis-
cosity data. Compare your result with the observed value1
of
506
X
cal/cm. s
.
K.
(b)
Compute the thermal conductivities of NO and CH, at
300K
and atmospheric pressure from the following data
for
these conditions:
p
X
lo7
(g/cm
-
s)
(cal/g-mole
.
K)
Compare your results with the experimental values given
in
Table
9.1-2.
9A.2
Computation of the Prandtl numbers for gases at
low
density.
(a)
By
using the Eucken formula and experimental heat
capacity data, estimate the Prandtl number at
1
atm and
300K
for each of the gases listed in the table.
(b)
For the same gases, compute the Prandtl number di-
rectly
by substituting the following value: of the physical
properties into the defining formula Pr
=
C,p/k, and com-
pare
the values with the results obtained in
(a).
All proper-
ties
are given at low pressure and
300K.
He
5.193 1.995 0.1546
Ar
0.5204 2.278 0.01784
H2
14.28 0.8944 0.1789
Air
1.001
1.854 0.02614
(9
0.8484
1.506 0.01661
H20
1.864
1
.041 0.02250
The entries in this table were prepared
from
functions provided by
T.
E.
Daubert,
R.
P.Danner,
H.
M.
Sibul, C. C. Stebbins,
J.
L.
Oscarson, R.
L.
Rowley, W.
V.
Wilding,
M.
E.
Adams, T.
L.
Marshall, and N.
A.
Zundel,
DIPPR
@
Data Compilation of Pure Compound
Properties,
Design Institute for Physical Property
Data@,
AKkE,
New York
(2000).
9A.3.
Estimation of the thermal conductivity of a dense
gas. Predict the thermal conductivity of methane at
110.4
atm and
127°F
by the following methods:
(a) Use Fig.
9.2-1.
Obtain the necessary critical properties
from Appendix
E.
(b) Use the Eucken formula to get the thermal conductiv-
ity at
127°F
and low pressure. Then apply a pressure cor-
rection by using Fig.
9.2-1.
The experimental value2 is
0.0282
Btu/hr ft
F.
Answer:
(a)
0.0294
Btu/hr. ft
-
F.
9A.4.
Prediction of the thermal conductivity of a gas
mixture. Calculate the thermal conductivity of a mixture
containing
20
mole
%
C02 and
80
mole
%
H2 at
1
atm
and
300K.
Use the data of Problem
9A.2
for your cal-
cula tions.
Answer:
0.1204
W/m
.
K
9A.5.
Estimation of the thermal conductivity of
a
pure
liquid. Predict the thermal conductivity of liquid H20 at
40°C
and
40
megabars pressure
(1
megabar
=
10'
dyn/cm2). The isothermal compressibility,
(1
/
p)
(dp/dp),
is
38
X
megabar-' and the density is
0.9938
g/cm3.
Assume that
2;
=
?,.
Answer:
0.375
Btu/hr
ft
.
F
9A.6.
Calculation of the Lorenz number.
(a) Application of kinetic theory to the "electron gas" in a
metap gives for the Lorenz number
in which
K
is the Boltzmann constant and
e
is the charge
on the electron. Compute
L
in the units given under
Eq.
9.5-1.
(b) The electrical resistivity,
l/k,,
of copper at 20°C is
1.72X
lop6
ohm cm. Estimate its thermal conduc-
tivity in W/m
e
K
using
Eq.
9A.6-1,
and
compare
your result with the experimental value given in
Table
9.1-4.
Answers:
(a)
2.44
X
lop8
volt'/^^;
(b)
416
W/m
.
K
9A.7.
Corroboration of the Wiedemann-Franz-Lorenz
law. Given the following experimental data at
20°C
for
pure metals, compute the corresponding values of the
Lorenz number,
L,
defined in
Eq.
9.5-1.
'
J.
M. Lenoir, W.
A.
Junk,
and
E.
W. Comings,
Chem.
Engr.
Prog., 49,539-542 (1953).
'
W.
G.
Kannuluik and
E.
H.
Carman,
Proc. Pkys. Soc.
J.
E.
Mayer and M.
G.
Mayer,
Statistical Mechanics,
Wiley,
(London),
65B,
701-704 (1952).
New York
(1946),
p.
412;
P.
Drude,
Ann. Phys., 1,566-613 (1900).
288
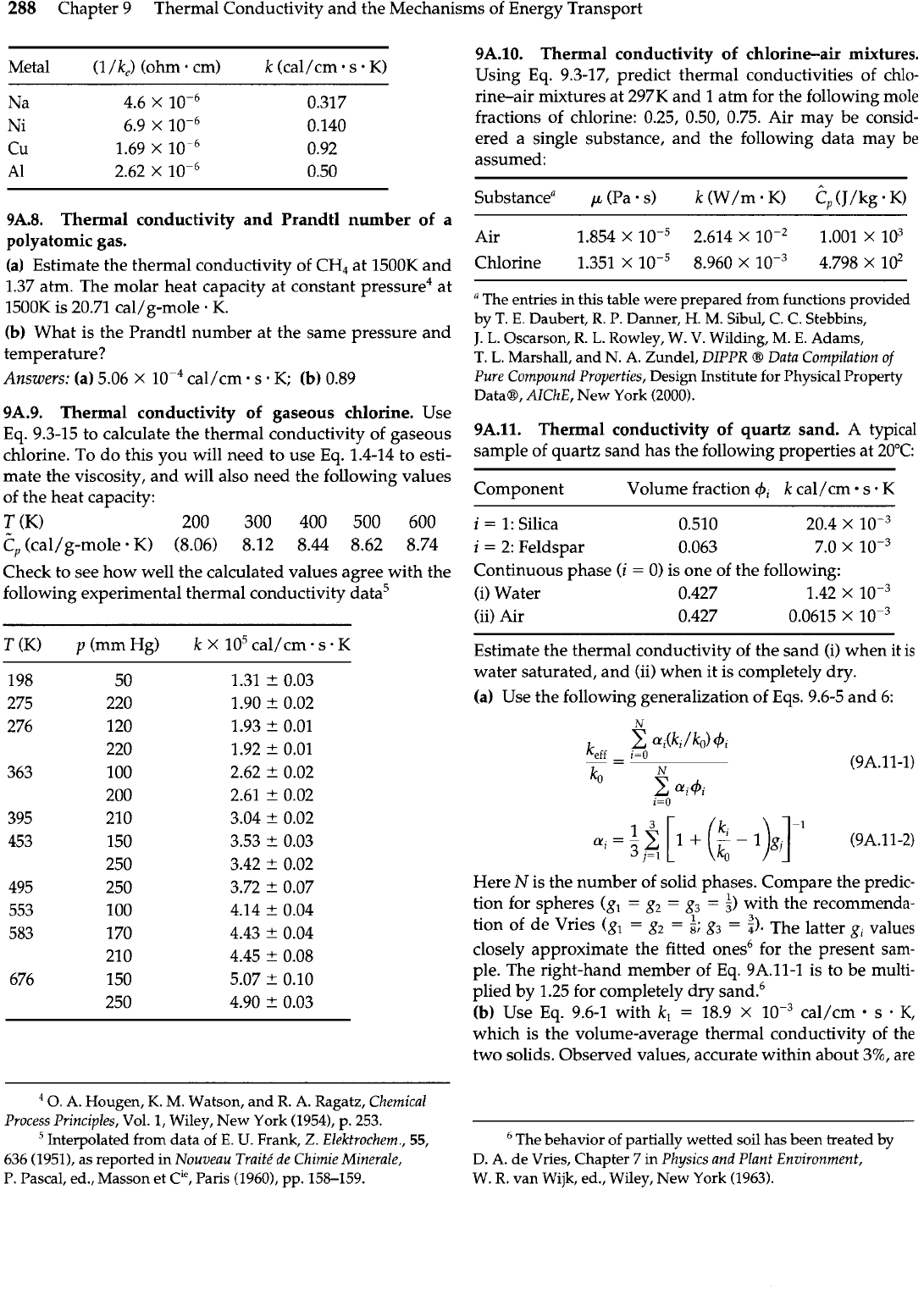
Chapter 9 Thermal Conductivity and the Mechanisi ms of Energy Transport
Metal
(1
/kc)
(ohm
.
cm)
k
(cal/cm
.
s
.
K)
9A.8.
Thermal conductivity and Prandtl number of a
polyatomic gas.
(a) Estimate the thermal conductivity of CH, at 1500K and
1.37 atm. The molar heat capacity at constant pressure4 at
1500K
is
20.71 cal/g-mole
.
K.
(b)
What is the Prandtl number at the same pressure and
temperature?
Answers:
(a) 5.06
X
lop4
cal/cm s
.
K; (b) 0.89
9A.9.
Thermal conductivity of gaseous chlorine. Use
Eq. 9.3-15 to calculate the thermal conductivity of gaseous
chlorine. To do this you will need to use Eq. 1.4-14 to esti-
mate the viscosity, and will also need the following values
of the heat capacity:
T
(K)
200 300 400 500 600
(cal/g-mole
.
K)
(8.06) 8.12 8.44 8.62 8.74
Check to see how well the calculated values agree with the
following experimental thermal conductivity data5
0.
A. Hougen,
K.
M. Watson, and R. A. Ragatz,
Chemical
Process Principles,
Vol.
1,
Wiley, New York (1954),
p.
253.
Interpolated from data of
E.
U.
Frank,
Z.
Elektrochem.,
55,
636 (1951), as reported in
Nouveau Trait6 de Chimie Minerale,
P. Pascal, ed., Masson et
Cie,
Paris (1960), pp. 158-159.
9A.10.
Thermal conductivity of chlorine-air mixtures.
Using
Eq.
9.3-17, predict thermal conductivities of chlo-
rine-air mixtures at 297K and
1
atm for the following mole
fractions of chlorine: 0.25, 0.50, 0.75. Air may be consid-
ered a single substance, and the following data may
be
assumed:
Substancea
p
(Pa s)
k
(W/m K)
e,
(J/kg
K)
Air 1.854
X
lo-'
2.614
X
lo-'
1.001
X
lo3
Chlorine
1.351
X
lo-'
8.960
X
4.798
X
10'
"
The entries in this table were prepared from functions provided
by T.
E.
Daubert, R.
P.
Danner,
H.
M.
Sibul,
C.
C.
Stebbins,
J.
L.
Oscarson,
R.
L.
Rowley, W. V. Wilding,
M.
E.
Adams,
T.
L.
Marshall, and N. A. Zundel,
DIPPR
@
Data Compilation of
Pure Compound Properties,
Design Institute for Physical Property
Data@,
AIChE,
New York (2000).
9A.11.
Thermal conductivity of quartz sand.
A
typical
sample of quartz sand has the following properties at 20°C:
Component Volume fraction
4,
k
cal/cm s
.
K
i
=
1: Silica 0.510 20.4
x
lo-3
i
=
2: Feldspar 0.063 7.0
X
Continuous phase
(i
=
0) is one of the following:
(i) Water 0.427 1.42
X
lop3
(ii) Air 0.427 0.0615
X
lop3
Estimate the thermal conductivity of the sand (i) when it is
water saturated, and (ii) when it is completely dry.
(a) Use the following generalization of Eqs. 9.6-5 and 6:
Here
N
is the number of solid phases. Compare the predic-
tion for spheres (g,
=
g2
=
g3
=
i)
with the recommenda-
tion
of
de Vries (gl
=
g2
=
i;
g3
=
9).
he
latter
gi
values
closely approximate the fitted ones6 for the present sam-
ple. The right-hand member of
Eq.
9A.11-1 is to be multi-
plied by 1.25 for completely dry sand.6
(b)
Use Eq. 9.6-1 with
k,
=
18.9
X
cal/cm s
.
K,
which is the volume-average thermal conductivity of the
two solids. Observed values, accurate within about 3%, are
The behavior of partially wetted soil has been treated by
D.
A. de Vries, Chapter
7
in
Physics and Plant Environment,
W. R. van Wijk, ed., Wiley, New York (1963).
Problems
289
6.2
and 0.58
x
W3
cal/cm
.
s
.
K
for wet and dry sand, re-
These three equations give the density corrections to the
spe~tively.~
viscosity and thermal conductivity of a hypothetical gas
Answers
in cal/cm. s
K
for wet and dry sand respectively:
made
up rigid
(a)
Eq.
9A.11-1 gives
keff
=
6.3
X
10" and 0.38
x
10" with
Enskog further suggested that for real gases, (i)
y
can
g,
=
g,
=
g3
=$
VS. 6.2
X
and 0.54
X
with
g,
=
g2
=
be
given empirically
and
g,
=
$.
(b)
Eq. 9.6-1 gives
keff
=
5.1
X
10" and 0.30
X
(9C.1-4)
9A.12.
Calculation of molecular diameters from trans-
port
properties.
where experimental
p-V-~
data are used, and (ii)
bo
can be
(a)
Determine the molecular diameter
d
for argon from Eq. determined by fitting the minimum in the curve of
1.4-9
and the experimental viscosity given in Problem 9A.2.
(p/pO)V
versus
Y.
(b)
Repeat part (a), but using Eq. 9.3-12 and the measured
thermal conductivity in Problem 9A.2. Compare this result
with the value obtained in (a).
(c)
Calculate and compare the values of the Lennard-Jones
collision diameter
a
from the same experimental data used
in
(a) and (b), using
E/K
from Table E.1.
(d)
What can be concluded from the above calculations?
Answer:
(a) 2.95
A;
(b)
1.86
A;
(c)
3.415
A
from Eq. 1.4-14,
3.409
A
from Eq. 9.3-13
9C.1.
Enskog theory for dense gases. ~nsko~~ devel-
oped
a
kinetic theory for the transport properties of dense
gases. He showed that for molecules that are idealized as
rigid
spheres of diameter
wo
(a)
A useful way to summarize the equation of state is to
use the correspon_ding-states presentation8 of
Z
=
Z(p,,
T,),
where Z
=
pV/XT,
p,
=
plp,, and T,
=
T/T,. Show
that the quantity
y
defined by Eq. 9C.1-4 can be com-
puted as a function of the reduced pressure and tempera-
ture from
1
+
(aln Z/aln
T,),
y=z
1
-
(aln Z/aln
p,),
-
(9C.1-5)
(b)
Show how Eqs. 9C.1-1, 2, and 5, together with the
Hougen-Watson Z-chart and the Uyehara-Watson
p/p,
chart in Fig. 1.3-1, can be used to develop a chart of k/k,. as
a function of p, and
T,.
What would be the limitations of
the resulting chart? Such a procedure (but using specific
~V-T
data instead of the Hougen-Watson Z-chart) was
used by Comings and Natham9
(c)
How might one use the Redlich and
won^'^
equation
(9C-1-2) of state
Here
p"
and
k"
are the low-pressure properties (computed,
a
(c
-
b)
=
RT
(9C.l-6)
for
example, from Eqs. 1.4-14 and 9.3-13),
V
is the molar
and
b0
=
jnNdf
where
'
is
Avogadro's
number'
for
the same purpose? The quantities
a
and
b
are constants
The quantity
y
is related to the equation of state of a gas of
charactenstic
of
each
gas.
rigid
spheres:
y
=
RT
-
1
=
($)
+
0.6250(!!)2
+
0.2869($r
+
.
(9C.1-3)
0.
A.
Hougen and K.
M.
Watson,
Chemical Process
Principles,
Vol.
11,
Wiley, New York
(1947),
p.
489.
D.
Enskog,
Kungliga Svenska Vetenskapsakademiens
E.
W.
Comings and
M.
F.
Nathan,
Ind. Eng. Chem.,
39,
Handlingar,
62,
No.
4
(1922),
in German. See also
J.
0.
Hirschfelder,
964-970 (1947).
C.
F.
Curtiss, and
R.
B.
Bird,
Molecular Theory of Gases and Liquids,
lo
0.
Redlich and
J.
N.
S.
Kwong,
Chem. Rev.,
44,233-244
2nd
printing with corrections
(1964),
pp.
647-652.
(1949).

Chapter
10
Shell
Energy Balances and
Temperature Distributions in
Solids and Laminar
Flow
Shell energy balances; boundary conditions
Heat conduction with an electrical heat source
Heat conduction with
a
nuclear heat source
Heat conduction with a viscous heat source
Heat conduction with a chemical heat source
Heat conduction through composite walls
Heat conduction in a cooling fin
Forced convection
Free convection
In Chapter
2
we saw how certain simple viscous flow problems are solved by a two-step
procedure: (i) a momentum balance is made over a thin slab or shell perpendicular to the
direction of momentum transport, which leads to a first-order differential equation that
gives the momentum flux distribution; (ii) then into the expression for the momentum
flux we insert Newton's law of viscosity, which leads to a first-order differential equa-
tion for the fluid velocity as a function of position. The integration constants that appear
are evaluated by using the boundary conditions, which specify the velocity or momen-
tum flux at the bounding surfaces.
In this chapter we show how a number of heat conduction problems are solved
by
an analogous procedure: (i) an energy balance is made over a thin slab or shell perpen-
dicular to the direction of the heat flow, and this balance leads to a first-order differential
equation from which the heat flux distribution is obtained; (ii) then into this expression
for the heat
flux,
we substitute Fourier's law of heat conduction, which gives a first-order
differential equation for the temperature as a function of position. The integration con-
stants are then determined by use of boundary conditions for the temperature or heat
flux at the bounding surfaces.
It should be clear from the similar wording of the preceding two paragraphs that
the
mathematical methods used in this chapter are the same as those introduced in Chapter
2-only the notation and terminology are different. However, we will encounter here a
number of physical phenomena that have no counterpart in Chapter
2.
After a brief introduction to the shell energy balance in §10.1, we give an analysis
of
the heat conduction in a series of uncomplicated systems. Although these examples are

s10.1
Shell
Energy Balances; Boundary Conditions
291
somewhat idealized, the results find application in numerous standard engineering cal-
culations. The problems were chosen to introduce the beginner to a number of important
physical concepts associated with the heat transfer field. In addition, they serve to show
how to use a variety of boundary conditions and to illustrate problem solving in Carte-
sian, cylindrical, and spherical coordinates. In §§10.2-10.5 we consider four kinds of heat
sources: electrical, nuclear, viscous, and chemical. In 9510.6 and 10.7 we cover two topics
with widespread applications-namely, heat flow through composite walls and heat
loss from fins. Finally, in §§10.8 and 10.9, we analyze two limiting cases of heat transfer
in moving fluids: forced convection and free convection. The study of these topics paves
the way for the general equations in Chapter 11.
$10.1
SHELL
ENERGY BALANCES; BOUNDARY
CONDITIONS
The problems discussed in this chapter are set up by means of shell energy balances. We
select a slab (or shell), the surfaces of which are normal to the direction of heat conduc-
tion, and then we write for this system a statement of the law of conservation of energy.
For
steady-state
(i.e., time-independent) systems, we write:
(rate energy of in
]
-
[rate energy of out
)
+
("te of
]
-
(rate of
)
energy in energy out
+
by convective by convective by molecular
by
molecular
transport
transport transport transport
rate of
The
convective transport
of energy was discussed in 59.7, and the
molecular transport
(heat
conduction) in 99.1. The
molecular work terms
were explained in s9.8. These three terms
can be added to give the "combined energy flux"
el
as shown in Eq. 9.8-6. In setting up
problems here (and in the next chapter) we will use the
e
vector along with the expres-
sion for the enthalpy in
Eq.
9.8-8. Note that in nonflow systems (for which
v
is zero) the
e
vector simplifies to the
q
vector, which is given by Fourier's law.
The
energy production
term in Eq. 10.1-1 includes (i) the degradation of electrical en-
ergy into heat, (ii) the heat produced by slowing down of neutrons and nuclear frag-
ments liberated in the fission process, (iii) the heat produced by viscous dissipation, and
(iv) the heat produced in chemical reactions. The chemical reaction heat source will be
discussed further in Chapter 19. Equation 10.1-1 is a statement of the first law of thermo-
dynamics, written for an "open" system at steady-state conditions. In Chapter 11 this
same statement-extended to unsteady-state systems-will be written as an equation of
change.
After Eq. 10.1-1 has been written for a thin slab or shell of material, the thickness of
the slab or shell is allowed to approach zero. This procedure leads ultimately to an ex-
pression for the temperature distribution containing constants of integration, which we
evaluate by use of boundary conditions. The commonest types of boundary conditions
are:
a.
The temperature may be specified at a surface.
b.
The heat flux normal to a surface may be given (this is equivalent to specifying
the normal component of the temperature gradient).
c.
At interfaces the continuity of temperature and of the heat flux normal to the in-
terface are required.

292
Chapter
10
Shell Energy Balances and Temperature Distributions in Solids and Laminar Flow
d.
At a solid-fluid interface, the normal heat flux component may be related to the
difference between the solid surface temperature To and the "bulk" fluid temper-
ature
Tb:
q
=
h(To
-
Td
(1
0.1-2)
This relation is referred to as Newton's law of cooling. It is not really a "law" but
rather the defining equation for
h,
which is called the heat transfer coejyrcient.
Chapter 14 deals with methods for estimating heat-transfer coefficients.
All four types of boundary conditions are encountered in this chapter. Still other kinds
of boundary conditions are possible, and they will be introduced as needed.
910.2
HEAT CONDUCTION WITH AN
ELECTRICAL HEAT SOURCE
The first system we consider is an electric wire of circular cross section with radius
R
and
electrical conductivity
k,
ohm-' cm-'. Through this wire there is an electric current with
current density
I
amp/cm2. The transmission of an electric current is an irreversible
process, and some electrical energy is converted into heat (thermal energy). The rate
of
heat production per unit volume is given by the expression
The quantity
S,
is the heat source resulting from electrical dissipation. We assume here
that the temperature rise in the wire is not so large that the temperature dependence
of
either the thermal or electrical conductivity need be considered. The surface of the wire
is maintained at temperature
To.
We now show how to find the radial temperature distri-
bution within the wire.
For the energy balance we take the system to be a cylindrical shell of thickness
Ar
and length
L
(see Fig. 10.2-1). Since v
=
0
in this system, the only contributions to the
en-
ergy balance are
Rate of heat in
across cylindrical (2.1rvL)qrlr)
=
(2.1rvLqr)l,
surface at r
Rate of heat out
across cylindrical
(2dr
+
Ar)L)(qrlr+Ar)
=
(2mLqr)lr+br
surface at r
+
Ar
Rate of thermal
energy production by (2mArL) S,
electrical dissipation
The notation
qr
means "heat flux in the
r
direction," and
(a
.)lr+8r
means "evaluated
at
r
+
Ar." Note that we take "in" and "out" to be in the positive r direction.
We now substitute these quantities into the energy balance of Eq. 9.1-1. Division by
2rLAr and taking the limit as Ar goes to zero gives
The expression on the left side is the first derivative of rq, with respect to r, so that
Eq.
10.2-5 becomes

s10.2 Heat Conduction with an Electrical Heat Source
293
Fig.
10.2-1.
An electrically heated wire, show-
ing the cylindrical shell over which the energy
Uniform heat
balance is made.
production
by
electrical
heating
st!
I
I
I
I
I
I
I
q4
Hqrir+Ar
1
I
Heat in
by
I I
Heat out
by
I
l
conduction
I
I
conduction
I
I
I
I
I I
I
I
--
/
I
This is a first-order differential equation for the energy flux, and it may be integrated to give
The integration constant
C,
must be zero because of the boundary condition that
B.C.
1: at
r
=
0,
q,
is not infinite (10.2-8)
Hence the final expression for the heat flux distribution is
I
I
This states that the heat flux increases linearly with
r.
We now substitute Fourier's law in the form
9,
=
-k(dT/dr) (see Eq. B.2-4) into
Eq.
10.2-9 to obtain
When
k
is assumed to be constant, this first-order differential equation can be integrated
to give
The integration constant is determined from
B.C.
2: atr=R, T=To
(10.2-12)
Hence
C,
=
(S,~'/4k)
+
To and Eq. 10.2-11 becomes
I
I
Equation 10.2-13 gives the temperature rise as a parabolic function of the distance r from
the wire axis.

294
Chapter
10
Shell Energy Balances and Temperature Distributions in Solids and Laminar Flow
Once the temperature and heat flux distributions are known, various information
about the system may be obtained:
(i)
Maximum temperature rise
(at
r
=
0)
(ii)
Average temperature rise
Thus the temperature rise, averaged over the cross section, is half the maximum temper-
ature rise.
(iii)
Heat outflow at the surface
(for a length
L
of wire)
This result is not surprising, since, at steady state, all the heat produced by electrical dis-
sipation in the volume
TR'L
must leave through the surface
r
=
R.
The reader, while going through this development, may well have had the feeling
of
de'ja
vu.
There is, after all, a pronounced similarity between the heated wire problem and
the viscous flow in a circular tube. Only the notation is different:
-
Tube flow Heated wire
First integration gives
r,(d
9Ay)
Second integration gives
UJY)
T(r)
-
To
Boundary condition at
r
=
0
rrz
=
finite
q,
=
finite
Boundary condition at
r
=
R
v,
=
0
T-To=O
Transport property
E".
k
Source term
(9'0
-
9'L)/L
s,
Assumptions
p
=
constant
k,
k,
=
constant
That is, when the quantities are properly chosen, the differential equations
and
the
boundary conditions for the two problems are identical, and the physical processes are
said to be "analogous." Not all problems in momentum transfer have analogs
in
energy
and mass transport. However, when such analogies can be found, they may be useful in
taking over known results from one field and applying them in another. For example,
the reader should have no trouble in finding a heat conduction analog for the viscous
flow in a liquid film on an inclined plane.
There are many examples of heat conduction problems in the electrical industry.'
The minimizing of temperature rises inside electrical machinery prolongs insulation life.
One example is the use of internally liquid-cooled stator conductors in very large
(500,000 kw)
AC
generators.
M.
Jakob,
Heat
Transfer,
Vol.
1,
Wiley,
New
York
(19491,
Chapter
10,
pp.
167-199.

510.2 Heat Conduction with an Electrical Heat Source
295
To illustrate further problems in electrical heating, we give two examples concern-
ing the temperature rise
in
wires: the first indicates the order of magnitude of the heating
effect, and the second shows how to handle different boundary conditions. In addition,
in Problem
10C.2
we show how to take into account the temperature dependence of the
thermal and electrical conductivities.
A copper wire has a radius of
2
mm and a length of 5 m. For what voltage drop would the
temperature rise at the wire axis be 10°C, if the surface temperature of the wire is 20°C?
Voltage Required for a
Given Temperature Rise
SOLUTION
in
a
Wire Heated
by
an
Electric Current
Combining
Eq.
10.2-14 and 10.2-1 gives
EXAMPLE
10.2.2
Heated Wire with
Specified Heat Transfer
The current density is related to the voltage drop
E
over a length
L
by
Hence
from which
For copper, the Lorenz number of 59.5 is k/keTo
=
2.23
X
lo-'
VO~P/K~.
Therefore, the voltage
drop needed to cause a 10°C temperature rise is
8
volt
v-
E
=
2(5000 2 mm mm)~2.23
X
10-
-
K (293)(10)K
=
(5000)(1.49
X
1oP4)(54.1)
=
40 volts
Repeat the analysis in 510.2, assuming that
To
is not known, but that instead the heat flux at
the wall is given by Newton's "law of cooling"
(Eq.
10.1-2). Assume that the heat transfer co-
efficient h and the ambient air temperature Tair are known.
Coefficient and SOLUTION I
Ambient Air
Temperature
The solution proceeds as before through
Eq.
10.2-11, but the second integration constant is de-
termined from
Eq.
10.1-2:
B.C.
2':
dT
atr=R, -k-=h(T-TaiJ (10.2-22)
dr
Substituting
Eq.
10.2-11 into
Eq.
10.2-22 gives
C2
=
(SeR/2h)
+
(S,R2/4k)
+
Tair, and the tem-
perature profile is then
From this the surface temperature of the wire is found to be
Ta,,
+
SJV2h.

296
Chapter 10 Shell Energy Balances and Temperature Distributions in Solids and Laminar Flow
SOLUTION
II
Another method makes use of the result obtained previously in
Eq.
10.2-13. Although
To
is
not known in the present problem, we can nonetheless use the result. From Eqs. 10.1-2 and
10.2-16 we can get the temperature difference
Substraction of Eq. 10.2-24 from Eq. 10.2-13 enables us to eliminate the unknown
To
and
gives
Eq.
10.2-23.
s10.3
HEAT CONDUCTION WITH
A
NUCLEAR HEAT SOURCE
We consider a spherical nuclear fuel element as shown in Fig. 10.3-1. It consists of
a
sphere of fissionable material with radius
R'~',
surrounded by a spherical shell of alu-
minum "cladding" with outer radius
R"'.
Inside the fuel element, fission fragments are
produced that have very high kinetic energies. Collisions between these fragments and
the atoms of the fissionable material provide the major source of thermal energy in the
reactor. Such a volume source of thermal energy resulting from nuclear fission we call
S,,
(cal/cm3.
s).
This source will not be uniform throughout the sphere of fissionable mater-
ial; it will be the smallest at the center of the sphere. For the purpose of this problem, we
assume that the source can be approximated by a simple parabolic function
Here
S,,,
is the volume rate of heat production at the center of the sphere, and
b
is a
di-
mensionless positive constant.
We select as the system a spherical shell of thickness
Ar
within the sphere of fission-
able material. Since the system is not in motion, the energy balance will consist only of
heat conduction terms and a source term. The various contributions to the energy bal-
ance are:
Coolant
Fig.
10.3-1.
A
spherical nuclear fuel assembly, showing
the temperature distribution within the system.
