Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


9.1
Fourier's Law of Heat Conduction (Molecular Energy Transport)
267
ture gradient, or, to put it pictorially, "heat slides downhill on the temperature versus
distance graph." Actually Eq. 9.1-2 is not really a "law" of nature, but rather a sugges-
tion, which has proven to be a very useful empiricism. However, it does have a theoreti-
cal basis, as discussed in Appendix
D.
If the temperature varies in all three directions, then we can write an equation like
Eq. 9.1-2 for each of the coordinate directions:
If each of these equations is multiplied by the appropriate unit vector and the equations
are then added, we get
which is the three-dimensional form of Fourier's law. This equation describes the molec-
ular transport of heat in isotropic media. By "isotropic" we mean that the material has
no preferred direction, so that heat is conducted with the same thermal conductivity
k
in
all directions.
Some solids, such as single noncubic crystals, fibrous materials, and laminates, are
anis~tropic.~ For such substances one has to replace Eq.
9.1-6
by
in which
K
is a symmetric second-order tensor called the
thermal conductivity tensor.
Thus, the heat flux vector does not point in the same direction as the temperature gra-
dient. For polymeric liquids in the shearing flow v,(y,
t),
the thermal conductivity may
increase above the equilibrium value by
20%
in the
x
direction and decrease by
10%
in
the
z
direction. Anisotropic heat conduction in packed beds is discussed briefly in
59.6.
J.
B. Fourier,
Thkorie analytique de la chaleur, CEuvres de Fourier,
Gauthier-Villars et Fils, Paris (1822).
(Baron) Jean-Baptiste-Joseph Fourier
(pronounced "Foo-ree-ay") (1768-1830) was not only a brilliant
mathematician and the originator of the Fourier series and the Fourier transform, but also famous as an
Egyptologist and a political figure (he was prefect of the province of Issre).
'Some authors prefer to write Eq. 9.1-2 in the form
in which
J,
is the "mechanical equivalent of heat," which displays explicitly the conversion of thermal
units into mechanical units. For example, in the c.g.s. system one would use the following units:
q,,
[=I
erg/cm2
-
s,
k
[=] cal/cm s
-
C,
T
[=I
C,
y
[=]
cm, and
J,
[=I
erg/cal. We will not use
Eq.
9.1-2a in this
book.
Although polymeric liquids at rest are isotropic, kinetic theory suggests that when they are
flowing the heat conduction is anisotropic [see
B.
H.
A.
A.
van den Brule,
Rheol. Acta,
28,257-266 (1989);
and
C.
F.
Curtiss and
R.
B.
Bird,
Advances
in
Polymer Science,
25,l-101 (1996)l. Experimental
measurements for shear and elongational flows have been reported by
D.
C. Venerus,
J.
D.
Schieber,
H.
Iddir,
J.
D.
Guzman, and A.
W.
Broerman,
Phys. Rev. Letters,
82,366-369 (1999); A.
W.
Broerman,
D.
C. Venerus, and
J.
D.
Schieber,
J.
Chem.
Phys.,
111,6965-6969 (1999);
H.
Iddir,
D.
C.
Venerus, and
J.
D.
Schieber,
AIChE
Journal,
46,610-615 (2000). For oriented polymer solids, enhanced thermal conductiv-
ity in the direction of orientation has been measured by
B.
Poulaert,
J.-C.
Chielens, C. Vandenhaende,
J.-P. Issi, and
R.
Legras,
Polymer Comm.,
31,14&151(1989). In connection with the bead spring models of
polymer thermal conductivity, it has been shown by
R.
B.
Bird, C. F. Curtiss, and
K.
J.
Beers
[Rheol. Acfa,
36,269-276 (1997)l that the predicted thermal conductivity is exceedingly sensitive to the form of the
potential energy used for describing the springs.

268
Chapter
9
Thermal Conductivity and the Mechanisms of Energy Transport
Another possible generalization of Eq. 9.1-6 is to include a term containing the time
derivative of
q
multiplied by a time constant, by analogy with the Maxwell model of lin-
ear viscoelasticity in Eq.
8.4-3.
There seems to be little experimental evidence that such
a
generalization is ~arranted.~
The reader will have noticed that Eq. 9.1-2 for heat conduction and Eq. 1.1-2 for vis-
cous flow are quite similar. In both equations the flux is proportional to the negative of
the gradient of a macroscopic variable, and the coefficient of proportionality is a physical
property characteristic of the material and dependent on the temperature and pressure.
For the situations in which there is three-dimensional transport, we find that Eq. 9.1-6 for
heat conduction and Eq. 1.2-7 for viscous flow differ in appearance. This difference
arises because energy is a scalar, whereas momentum is a vector, and the heat flux
q
is
a
vector with three components, whereas the momentum flux
I
is a second-order tensor
with nine components. We can anticipate that the transport of energy and momentum
will in general not be mathematically analogous except in certain geometrically simple
situations.
In addition to the thermal conductivity
k,
defined by Eq. 9.1-2, a quantity known
as
the thermal
difisivity
a
is widely used. It is defined as
Here
Sp
is the heat capacity at constant pressure; the circumflex
(A)
over the symbol indi-
cates a quantity "per unit mass." Occasionally we will need to use the symbol in
which the tilde
(-)
over the symbol stands for a quantity "per mole."
The thermal diffusivity
a
has the same dimensions as the kinematic viscosity
v-
namely, (length)*/time. When the assumption of constant physical properties is made,
the quantities
v
and
CY
occur in similar ways in the equations of change for momentum
and energy transport. Their ratio
v/a
indicates the relative ease of momentum and en-
ergy transport in flow systems. This dimensionless ratio
is called the Prandtl number.%nother dimensionless group that we will encounter in
subsequent chapters is the Piclet number:
P6
=
RePr.
The units that are commonly used for thermal conductivity and related quantities
are given in Table 9.1-1. Other units, as well as the interrelations among the various sys-
tems, may be found in Appendix
F.
Thermal conductivity can vary all the way from about 0.01 W/m
K
for gases to
about 1000 W/m
.
K
for pure metals. Some experimental values of the thermal con-
The linear theory of thermoviscoelasticity does predict relaxation effects in heat conduction,
as discussed by
R.
M.
Christensen,
Theory of Viscoelasticity,
Academic Press, 2nd edition (1982). The
effect
has
also been found from a kinetic theory treatment of the energy equation
by
R.
B.
Bird and
C.
F.
Curtiss,
J.
Non-Newtonian
Fluid
Mechanics,
79,255-259 (1998).
"his dimensionless group, named for Ludwig Prandtl, involves only
the
physical properties of
the fluid.
Jean-Claude-Eug&ne
Pkclet
(pronounced "Pay-clay" with the second syllable accented)
(1
793-1857) authored several books including one on heat conduction.
9.1 Fourier's Law of Heat Conduction (Molecular Energy Transport)
269
Table
9.1-1 Summary of Units for Quantities in Eqs. 9.1-2 and
9
SI c.g.s. British
call cm2
-
s Btu/hr. ft2
C
F
cm ft
cal/cm
-
s.
C
Btu/hr. ft
. F
cal/C
a
g
Btu/F
lb,
cm2
/
s ft2/s
g/cm. s Ib,/ft
-
hr
-
Note:
The watt
(W)
is the same as J/s, the joule
(J)
is the same as
N
-
m,
the newton
(N)
is
kg.
m/s2, and the Pascal (Pa) is N/m2. For more
information on interconversion of units, see Appendix F.
ductivity of gases, liquids, liquid metals, and solids are given in Tables 9.1-2,
9.1-3,
9.1-4, and
9.1-5.
In making calculations, experimental values should be used when
possible. In the absence of experimental data, one can make estimates by using the
methods outlined in the next several sections or by consulting various engineering
handbook^.^
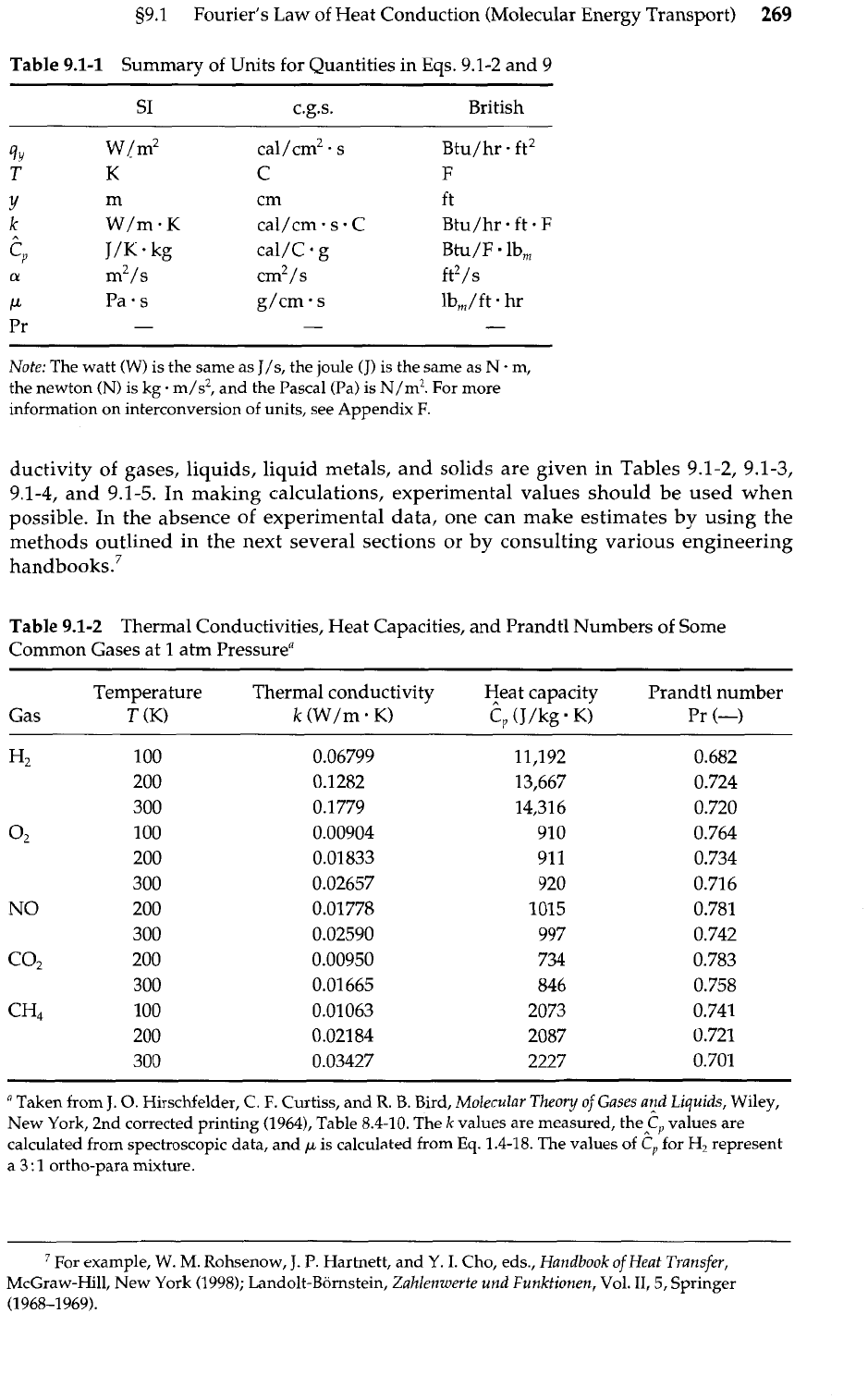
Table
9.1-2 Thermal Conductivities, Heat Capacities, and Prandtl Numbers of Some
Common Gases at
1
atm Pressuren
Temperature Thermal conductivity Heat capacity Prandtl number
Gas
T
(K)
k
(W/m.
K)
C,
(J/kg
K)
Pr
(-4
Taken from
J.
0.
Hirschfelder,
C.
F.
Curtiss, and
R.
B. Bird,
Molecular Theory of Gases and Liquids,
Wiley,
New York, 2nd corrected printing (1964), Table
8.4-10.
The
k
values are measured, the& values are
calculated from spectroscopic data, and
p
is calculated from
Eq.
1.4-18. The values of
C,,
for
H,
represent
a
3:
1
ortho-para mixture.
For example,
W.
M. Rohsenow,
J.
P.
Hartnett, and Y.
I.
Cho, eds.,
Handbook of Heat Transfer,
McGraw-Hill, New York (1998); Landolt-Bornstein,
Zahlenwerte und Funktionen,
Vol.
II,5,
Springer
(1968-1969).
270
Chapter
9
Thermal Conductivity and the Mechanisms of Energy Transport
Measurement
of
Thermal
Conductivity
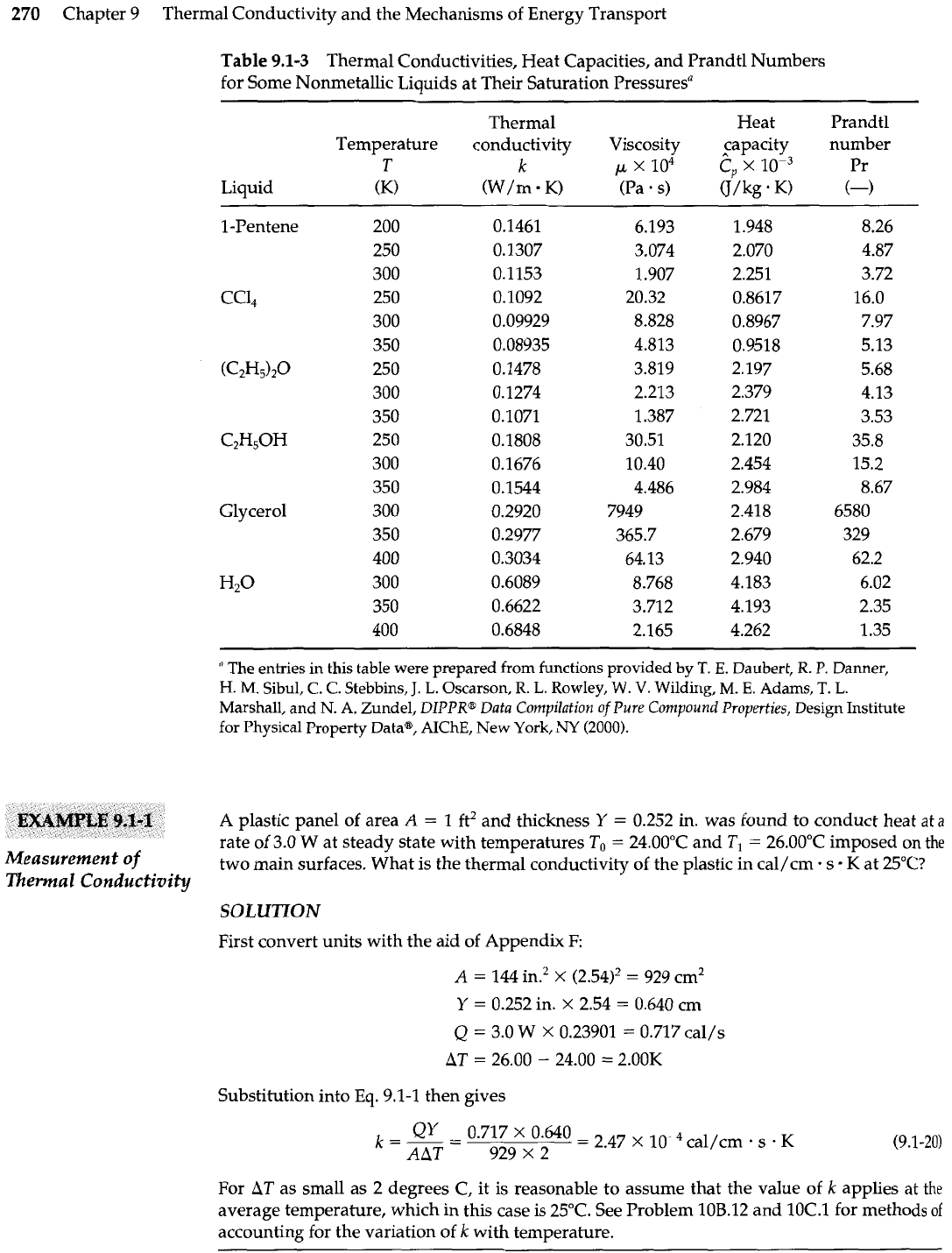
Table
9.1-3
Thermal Conductivities, Heat Capacities, and Prandtl Numbers
for Some Nonmetallic Liquids at Their Saturation Pressuresa
Thermal Heat Prandtl
Temperature conductivity Viscosity capacity number
T
k
x
lo4
S,
x
lop3
Pr
Liquid
(K)
(W/m
K)
(Pa
.
s)
U/kg
+
K)
(-1
1
-Pentene
CCl,
(C2H5)20
C2H50H
Glycerol
H2O
a
The entries in this table were prepared from functions provided by
T.
E.
Daubert,
R.
P.
Danner,
H.
M.
Sibul,
C.
C.
Stebbins,
J.
L.
Oscarson,
R.
L.
Rowley,
W.
V.
Wilding,
M.
E.
Adams,
T.
L.
Marshall, and
N.
A.
Zundel,
DIPPRB Data Compilation
of
Pure Compound Properties,
Design Institute
for
Physical Property Data@, AIChE, New York,
NY
(2000).
A
plastic panel of area
A
=
1
ft2 and thickness
Y
=
0.252
in. was found to conduct heat
at
a
rate of 3.0
W
at steady state with temperatures
To
=
24.00"C and
T,
=
26.00"C imposed on
the
two main surfaces. What is the thermal conductivity of the plastic in cal/cm. s
K
at 25"C?
SOLUTION
First convert units with the aid of Appendix
F:
A
=
144 in.2
X
(2.54)'
=
929
cm2
Y
=
0.252 in.
X
2.54
=
0.640 cm
Q
=
3.0
W
X
0.23901
=
0.717 cal/s
AT
=
26.00
-
24.00
=
2.00K
Substitution into
Eq.
9.1-1 then gives
For
AT
as small as 2 degrees
C,
it is reasonable to assume that the value of
k
applies
at
the
average temperature, which in this case is 25°C. See Problem 10B.12 and 10C.l for methods
of
accounting for the variation of
k
with temperature.
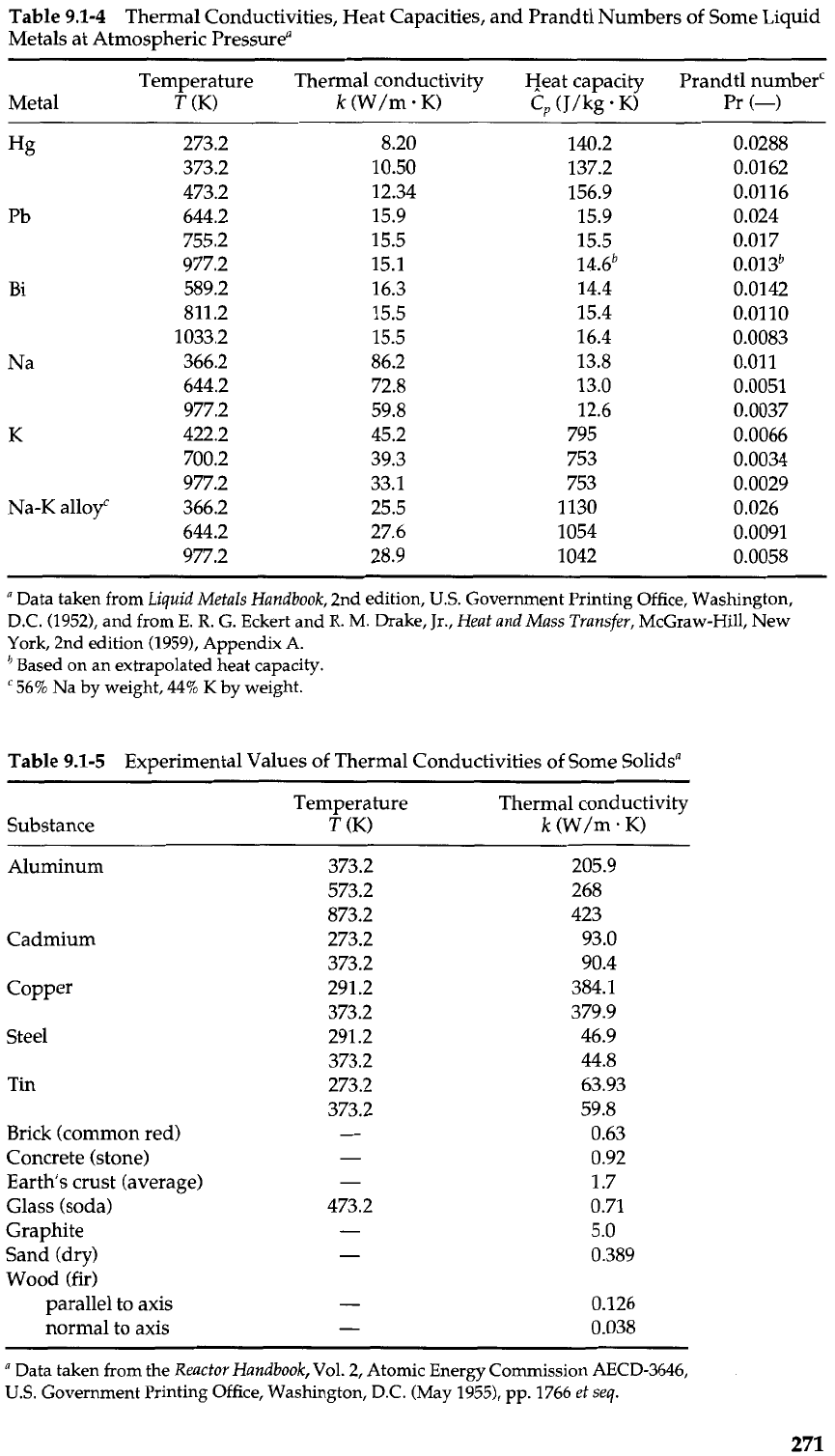
Table
9.1-4
Thermal Conductivities, Heat Capacities, and Prandtl Numbers of Some Liquid
Metals at Atmospheric Pressurea
Temperature Thermal conductivity Heat capacity Prandtl numberc
Metal
T
(K)
k
(W/m K)
c,
(J/kg
.
K)
Pr
(-)
"
Data taken from
Liquid Metals Handbook,
2nd edition,
US.
Government Printing Office, Washington,
D.C.
(1952), and from
E.
R.
G. Eckert and
R.
M.
Drake, Jr.,
Heat and Mass Transfer,
McGraw-Hill, New
York, 2nd edition (19591, Appendix A.
*
Based on an extrapolated heat capacity.
'
56% Na by weight,
44%
K
by weight.
Table
9.1-5
Experimental Values of Thermal Conductivities of Some Solidsa
Substance
Temperature Thermal conductivity
T
(K)
k
(W/m. K)
Aluminum
Cadmium
Copper
Steel
Tin
Brick (common red)
Concrete (stone)
Earth's crust (average)
Glass (soda)
Graphite
Sand (dry)
Wood (fir)
parallel to axis
normal to axis
"
Data taken from the
Reactor Handbook,
Vol. 2, Atomic Energy Commission AECD-3646,
U.S.
Government Printing Office, Washington,
D.C.
(May 19551, pp. 1766
et seq.
272
Chapter 9
Thermal Conductivity and the Mechanisms of Energy Transport
59.2
TEMPERATURE AND PRESSURE DEPENDENCE
OF
THERMAL CONDUCTIVITY
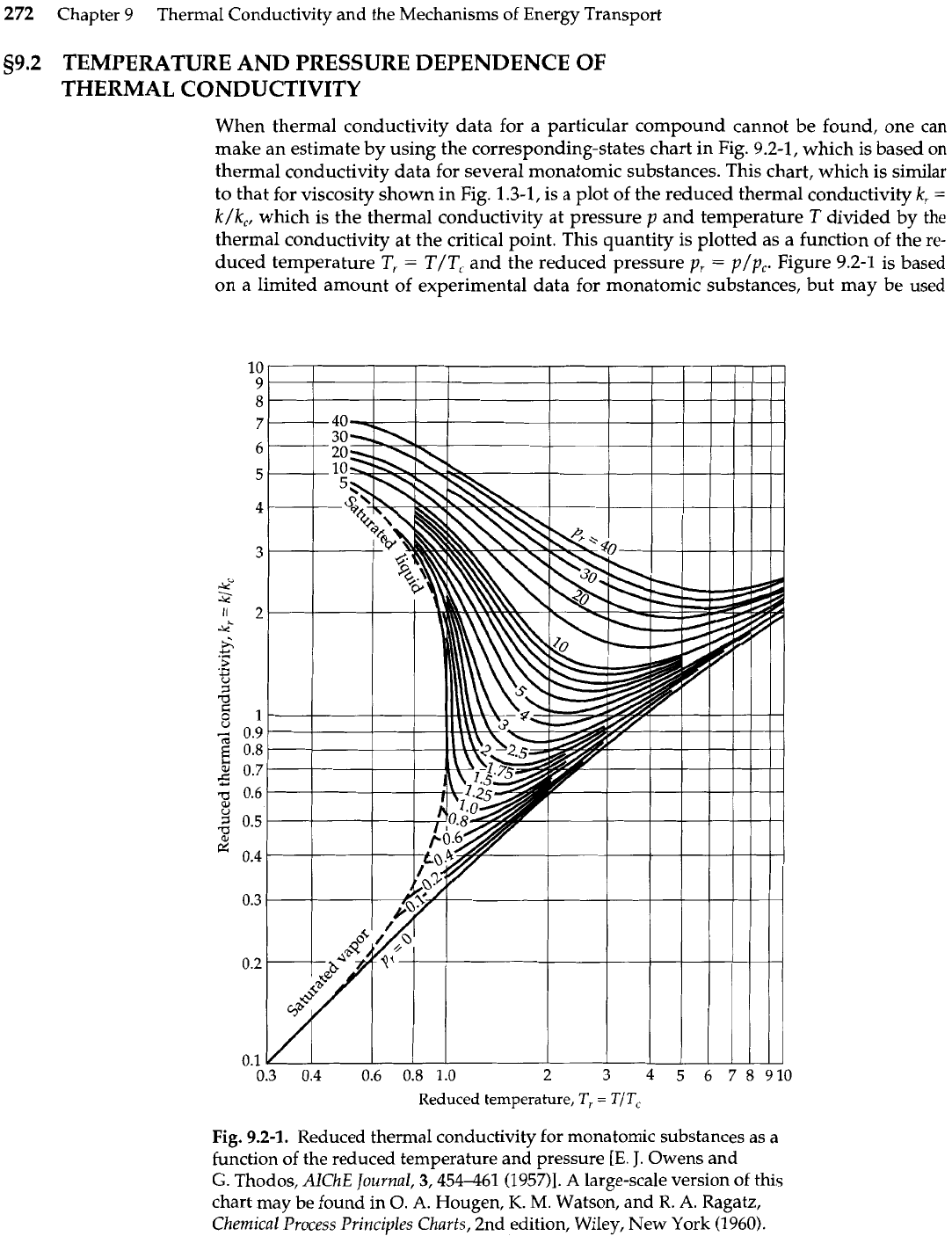
When thermal conductivity data for a particular compound cannot be found, one can
make an estimate by using the corresponding-states chart in Fig. 9.2-1, which is based on
thermal conductivity data for several monatomic substances. This chart, which is similar
to that for viscosity shown in Fig.
1.3-1,
is a plot of the reduced thermal conductivity
k,
=
k/k,,
which is the thermal conductivity at pressure
p
and temperature
T
divided by the
thermal conductivity at the critical point. This quantity is plotted as a function of the re-
duced temperature T,
=
T/T, and the reduced pressure p,
=
p/~,.
Figure 9.2-1 is based
on a limited amount of experimental data for monatomic substances, but may be used
Fig.
9.2-1.
Reduced thermal conductivity for monatomic substances as a
function of the reduced temperature and pressure
[E.
J.
Owens and
G.
Thodos, AlChE Journal, 3,454461 (1957)l.
A
large-scale version of this
chart may be found in
0.
A.
Hougen,
K.
M.
Watson, and R.
A.
Ragatz,
Chemical Process Principles Charts, 2nd edition, Wiley, New York (1960).

s9.2 Temperature and Pressure Dependence of Thermal Conductivity
273
for rough estimates for polyatomic materials. It should
not
be used in the neighborhood
of the critical point.'
It can be seen that the thermal conductivity of a gas approaches a limiting function
of
T
at low pressures; for most gases this limit is reached at about
1
atm pressure. The
thermal conductivities of
gases
at low density
increase
with increasing temperature,
whereas the thermal conductivities of most
liquids
decrease
with increasing temperature.
The correlation is less reliable in the liquid region; polar or associated liquids, such as
water, may exhibit a maximum in the curve of
k
versus
T.
The main virtue of the
corresponding-states chart is that one gets a global view of the behavior of the thermal
conductivity of gases and liquids.
The quantity
kc
may be estimated in one of two ways: (i) given
k
at a known temper-
ature and pressure, preferably close to the conditions at which
k
is to be estimated, one
can read
k,
from the chart and compute
kc
=
k/k,;
or (ii) one can estimate a value of
k
in
the low-density region by the methods given in 99.3 and then proceed as in (i). Values of
kc
obtained by method (i) are given in Appendix
E.
For mixtures, one might estimate the thermal conductivity by methods analogous to
those described in 91.3. Very little is known about the accuracy of pseudocritical proce-
dures as applied to thermal conductivity, largely because there are so few data on mix-
tures at elevated pressures.
Estimate the thermal conductivity of ethane at 153'F and 191.9 atm from the experimental
value2
k
=
0.0159 Btu/hr. ft
.
F at 1 atm and 153°F.
Effect
of
Pressure on
Thermal
Conductivity
SOLmON
Since a measured value of
k
is known, we use method (i). First we calculate
p,
and
T,
at the
condition of the measured value:
From Fig. 9.2-1 we read
k,
=
0.36. Hence
kc
is
At 153°F
(T,
=
1.115) and 191.9 atm
(p,
=
3.98), we read from the chart
k,
=
2.07. The predicted
thermal conductivity is then
An observed value of 0.0453 Btu/hr
ft F has been reported.' The poor agreement shows that
one should not rely heavily on this correlation for polyatomic substances nor for conditions
near the critical point.
In the vicinity of the critical point, where the thermal conductivity diverges, it is customary to
write
k
=
kb
+
Ak,
where
kb
is the "background" contribution and
Ak
is the "critical enhancement''
contribution. The
kc
being used in the corresponding states correlation is the background contribution.
For the behavior of transport properties near the critical point, see
J.
V.
Sengers and
J.
Luettmer
Strathmann, in
Transport Properties
of
Fluids
(J.
H.
Dymond,
J.
Millat, and C.
A.
Nieto de Castro, eds.),
Cambridge University Press
(1995);
E.
P.
Sakonidou,
H.
R.
van den Berg, C.
A.
ten Seldam, and
J.
V.
Sengers,
J.
Chem. Phys.,
105,10535-10555 (1996)
and
109,717-736 (1998).
J.
M.
Lenoir,
W.
A.
Junk, and
E.
W.
Comings,
Chem. Eng.
Progr.,
49,539-542 (1949).

274
Chapter
9
Thermal Conductivity and the Mechanisms of Energy Transport
59.3
THEORY OF THERMAL CONDUCTIVITY
OF GASES
AT
LOW DENSITY
The thermal conductivities of dilute
monatomic
gases are well understood and can be
de-
scribed by the kinetic theory of gases at low density. Although detailed theories for
poly-
atomic
gases have been developed,' it is customary to use some simple approximate
theories. Here, as in 91.5, we give a simplified mean free path derivation for monatomic
gases, and then summarize the result of the Chapman-Enskog kinetic theory of gases.
We use the model of rigid, nonattracting spheres of mass
m
and diameter
d.
The gas
as a whole
is
at rest
(v
=
O),
but the molecular motions must be accounted for.
As in 91.5, we use the following results for a rigid-sphere gas:
ii
=
@
=
mean molecular speed (9.3-1)
Z
=
in@
=
wall collision frequency per unit area
(9.3-2)
h
=
=
mean free path
*d2n
The molecules reaching any plane in the gas have had, on an average, their last collision
at a distance
a
from the plane, where
In these equations
K
is the Boltzmann constant,
n
is the number of molecules per
unit
volume, and
m
is the mass of a molecule.
The only form of energy that can be exchanged in a collision between two smooth
rigid spheres is translational energy. The mean translational energy per molecule under
equilibrium conditions is
as shown in Prob. 1C.1. For such a gas, the molar heat capacity at constant volume is
in which
R
is the gas constant. Equation 9.3-6 is satisfactory for monatomic gases up
to
temperatures of several thousand degrees.
To determine the thermal conductivity, we examine the behavior of the gas under
a
temperature gradient
dT/dy
(see Fig. 9.3-1). We assume that Eqs. 9.3-1 to 6 remain valid
in this nonequilibrium situation, except that
$rnZ
in
Eq.
9.3-5 is taken as the average
ki-
netic energy for molecules that had their last collision in a region of temperature
T.
The
heat flux
qy
across any plane of constant
y
is found by summing the kinetic energies
of
the molecules that cross the plane per unit time in the positive
y
direction and subtract-
ing the kinetic energies of the equal number that cross in the negative
y
direction:
'
C.
S.
Wang Chang,
G.
E.
Uhlenbeck, and
J.
de Boer,
Studies
in
Statistical Mechanics,
Wiley-
Interscience,
New
York, Vol.
I1
(1964,
pp.
241-265;
E.
A.
Mason and
L.
Monchick,
J.
Chem. Phys.,
35,
1676-1697 (1961)
and
36,1622-1639,2746-2757 (1962);
L.
Monchick,
A.
N.
G.
Pereira, and
E.
A.
Mason,
J.
Chem. Phys.,
42,3241-3256 (1965).
For
an introduction to the kinetic theory of the transport properties,
see R.
S.
Berry,
S.
A.
Rice, and
J.
Ross,
Physical Chemistry,
2nd edition
(2000),
Chapter
28.

s9.3
Theory of Thermal Conductivity of Gases at Low Density
275
Fig.
9.3-1.
Molecular transport
of (kinetic) energy from plane
at
(y
-
a)
to plane at
y.
Equation 9.3-7 is based on the assumption that all molecules have velocities representa-
tive of the region of their last collision and that the temperature profile
T(y)
is linear for a
distance of several mean free paths. In view of the latter assumption we may write
By combining the last three equations we get
This corresponds to Fourier's law of heat conduction
(Eq.
9.1-2) with the thermal con-
ductivity given by
k
=
fn~iih
=
iPtvii~
(monatomic gas) (9.3-1 1)
in which
p
=
nrn is the gas density, and
kV
=
fK/m
(from Eq. 9.3-6).
Substitution of the expressions for
ii
and
A
from Eqs. 9.3-1 and 3 then gives
k
=
-
- -
-
tv
(monatomic gas)
,d2
3%-
rd2
which is the thermal conductivity of a dilute gas composed of rigid spheres of diameter
d.
This equation predicts that
k
is
independent of pressure. Figure 9.2-1 indicates that this
prediction is in good agreement with experimental data up to about 10 atm for most
gases. The predicted temperature dependence is too weak, as was the case for viscosity.
For a more accurate treatment of the monatomic gas, we turn again to the rigorous
Chapman-Enskog treatment discussed in 51.5. The Chapman-Enskog formula2 for the
thermal conductivity of a monatomic gas at low density and temperature
T
is
k
=
-
vmii
25w?v
or
k=
1.9891
X
10'-
(monatomic gas) (9.3-13)
32
.rra21nk
a
2CRk
In the second form of this equation,
k
[=I
cal/cm
.
s
K,
T
[=I
K,
a
[=I
A,
and the "colli-
sion integral" for thermal conductivity,
SZk,
is identical to that for viscosity,
a,
in 51.4.
J.
0.
Hirschfelder,
C.
F.
Curtiss, and
R.
B.
Bird,
Molecular Theory of Gases
and
Liquids,
Wiley, New
York, 2nd corrected printing
(19641,
p.
534.

276
Chapter
9
Thermal Conductivity and the Mechanisms of Energy Transport
Values of
ilk
=
a,
are given for the Lennard-Jones intermolecular potential in Table
E.2
as a function of the dimensionless temperature
KT/&.
Equation 9.3-13, together with
Table E.2, has been found to be remarkably accurate for predicting thermal conductivi-
ties of
monatomic
gases when the parameters
o
and
E
deduced from viscosity measure-
ments are used (that is, the values given in Table E.l).
Equation 9.3-13 is very similar to the corresponding viscosity formula, Eq. 1.4-14.
From these two equations we can then get
15
R
k
=
--
5
-
p
=
2
Cvp
(monatomic gas) (9.3-14)
The simplified rigid-sphere theory (see Eqs. 1.4-8 and 9.3-11) gives
k
=
evP
and is thus
in
error by a factor 2.5. This is not surprising in view of the many approximations that were
made in the simple treatment.
So far we have discussed only
monatomic
gases. We know from the discussion in
50.3
that, in binary collisions between diatomic molecules, there may be interchanges be-
tween kinetic and internal (i.e., vibrational and rotational) energy. Such interchanges are
not taken into account in the Chapman-Enskog theory for monatomic gases. It can there-
fore be anticipated that the Chapman-Enskog theory will not be adequate for describing
the thermal conductivity of polyatomic molecules.
A
simple semiempirical method of accounting for the energy exchange in poly-
atomic gases was developed by E~cken.~ His equation for thermal conductivity of
a
polyatomic gas at low density is
k
=
(*
C,
+
-
El)
-
p
(polyatomic gas)
This
Eucken formula
includes the monatomic formula (Eq. 9.3-14) as a special case,
be-
cause
?,
=
~(R/M)
for monatomic gases. Hirschfelder4 obtained a formula similar to that
of Eucken by using multicomponent-mixture theory (see Example 19.4-4). Other theo-
ries, correlations, and empirical formulas are also a~ailable.~,~
Equation 9.3-15 provides a simple method for estimating the Prandtl number,
de-
fined in Eq.
9.1-8:
-
This equation is fairly satisfactory for nonpolar polyatomic gases at low density, as
can
be seen in Table 9.3-1; it is less accurate for polar molecules.
The thermal conductivities for gas mixtures at low density may be estimated by
a
method7 analogous to that previously given for viscosity (see Eqs. 1.4-15 and 16):
The
x,
are the mole fractions, and the
k,
are the thermal conductivities of the pure chem-
ical species. The coefficients
are identical to those appearing
in
the viscosity equation
-
-
A.
Eucken,
Physik.
Z.,
14,324-333 (1913); "Eucken" is pronounced "Oy-ken."
J.
0.
Hirschfelder,
J.
Chem. Phys.,
26,274-281,282-285 (1957).
J.
H. Ferziger and H.
G.
Kaper,
Mathematical Theory of Transport Processes in Gases,
North-Holland,
Amsterdam (1972).
'
R.
C.
Reid,
J.
M.
Prausnitz, and
B. E.
Poling,
The Properties of Gases
and
Liquids,
McGraw-Hill,
New
York, 4th edition (1987).
E.
A. Mason and
S.
C.
Saxena,
Physics of Fluids,
1,361-369 (1958). Their method is an
approximation to a more accurate method given by
J.
0.
Hirschfelder,
J.
Chem. Phys.,
26,274-281,
282-285 (1957). With Professor Mason's approval we have omitted here an empirical factor
1.065
in his
Qii
expression for
i
#
j
to establish self-consistency for mixtures of identical species.
