Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

93.6 MoIecular Theories for Polymeric Liquids

257

Fig.

8.6-5.

Steady elongational

viscosity

as a function of the

elongation rate

according to

the FENE-P dumbbell model.

100

The time constant

given

AHb/(b

3). [From

3(70

VS)

B. Bird,

J. Dotson, and

Johnson,

Non-Newton-

ion

Fluid

Mech., 7,213-235

(1980).1

0.01 0.1 1 10 100

(b)

For steady-state elongational flow we get

This set of equations leads to a cubic equation for

rP,,,

from which the elongational vis-

cosity can be obtained (see Fig. 8.6-5). Limited experimental data on polymer solutions indi-

cate that the shapes of the curves are probably approximately correct.

The limiting expressions for the elongational viscosity are

For

Having found the stresses in the system, we can then get the average stretching of the mole-

cules as a function of the elongation rate; this is shown in Fig. 8.6-6.

It is worth noting that for a typical value of b-say, 50-the elongational viscosity can in-

crease by a factor of about 30 as the elongation rate increases, thereby having a profound ef-

fect on flows

which there is a strong elongational component.7

The

FENE-P

and Giesekus models have been used successfully to describe the details of turbulent

drag reduction, which

closely related to elongational viscosity, by

Sureshkumar,

Beris and

Handler,

Phys. Fluids,

9,743-755 (1997),

and

Dimitropoulos,

Sureshkumar, and

Beris,

Non-Newtonian Fluid Mechanics,

79,433-468 (1998).

Fig.

8.6-6.

Molecular stretching as

a function of the elongation rate

steady elongational flow, as

predicted by the FENE-P dumb-

bell model.

The

time constant is

givenbyhe=A,b/(b+3).[From

Bird, P.

Dotson, and

0.01 0.1 1 10 100

Johnson,

Non-Newtonian

Fluid

Mech., 7,213-235

(1980).1

0.01

1111 111 111 111

258

Chapter 8 Polymeric Liquids

QUESTIONS FOR DISCUSSION

Compare the behavior of Newtonian liquids and polymeric liquids in the various experi-

ments discussed in ss8.1 and 8.2.

Why do we deal only with differences in normal stresses for incompressible liquids (see Eqs.

8.2-2 and 3)?

In Fig. 8.2-2 the postulated velocity profile is linear in

What would you expect the velocity

distribution to look like if the gap between the plates were not small and the fluid had a very

low viscosity?

How is the parameter

in Eq. 8.3-3 related to the parameter

in Eq. 8.3-4? How is it related to

the slope of the non-Newtonian velocity curve from the dumbbell kinetic theory model in

@.6?

What limitations have to be placed on use of the generalized Newtonian models and the lin-

ear viscoelastic models?

Compare and contrast Examples 8.4-1 and 2 regarding the geometry of the flow system and

the assumptions regarding the velocity profiles.

To what extent does the Oldroyd model in Eq. 8.5-3 include a generalized Newtonian model

and a linear viscoelastic model? Can the Oldroyd model describe effects that are not de-

scribed by these other models?

Why is it necessary to put restrictions on the parameters in the Oldroyd model? What is the

relation between these restrictions and the subject of rheometry?

What advantages do molecular expressions for the stress tensor have over the empirical ex-

pressions?

For what kinds of industrial problems would you use the various kinds of models described

in this chapter?

Why may the power law model be unsatisfactory for describing the axial flow in an annulus?

PROBLEMS

8A.1

Flow of a polyisoprene solution in a pipe.

13.5% (by weight) solution of polyisoprene in

isopentane has the following power law parameters at 323

0.2

and

lo3

Pa. sn.

is being pumped (in laminar flow) through a horizontal pipe that has a length of 10.2 m and

an internal diameter of 1.3 cm. It is desired to use another pipe with a length of 30.6 m with

the same mass flow rate and the same pressure drop. What should the pipe radius be?

8A.2

Pumping of a polyethylene oxide solution.

1% aqueous solution of polyethylene oxide

333

has power law parameters

0.6 and

0.50 Pa

sn. The solution is being pumped

between two tanks, with the first tank at pressure

and the second at pressure

p,.

The pipe

carrying the solution has a length of 14.7m and an internal diameter of 0.27 m.

It has been decided to replace the single pipe by a pair of pipes of the same length, but

with smaller diameter. What diameter should these pipes have so that the mass flow rate will

be the same as in the single pipe?

8B.1

Flow of a polymeric film. Work the problem in s2.2 for the power law fluid. Show that the

result simplifies properly to the Newtonian result.

8B.2

Power law flow in a narrow slit. In Example 8.3-2 show how to derive the velocity distribu-

tion for the region

-B

Is it possible to combine this result with that in Eq. 8.3-13 into

one equation?

8B.3

Non-Newtonian flow in an annulus. Rework Problem

2B.7

for the annular flow of a power

law fluid with the flow being driven by the axial motion of the inner cylinder.

(a)

Show that the velocity distribution for the fluid is

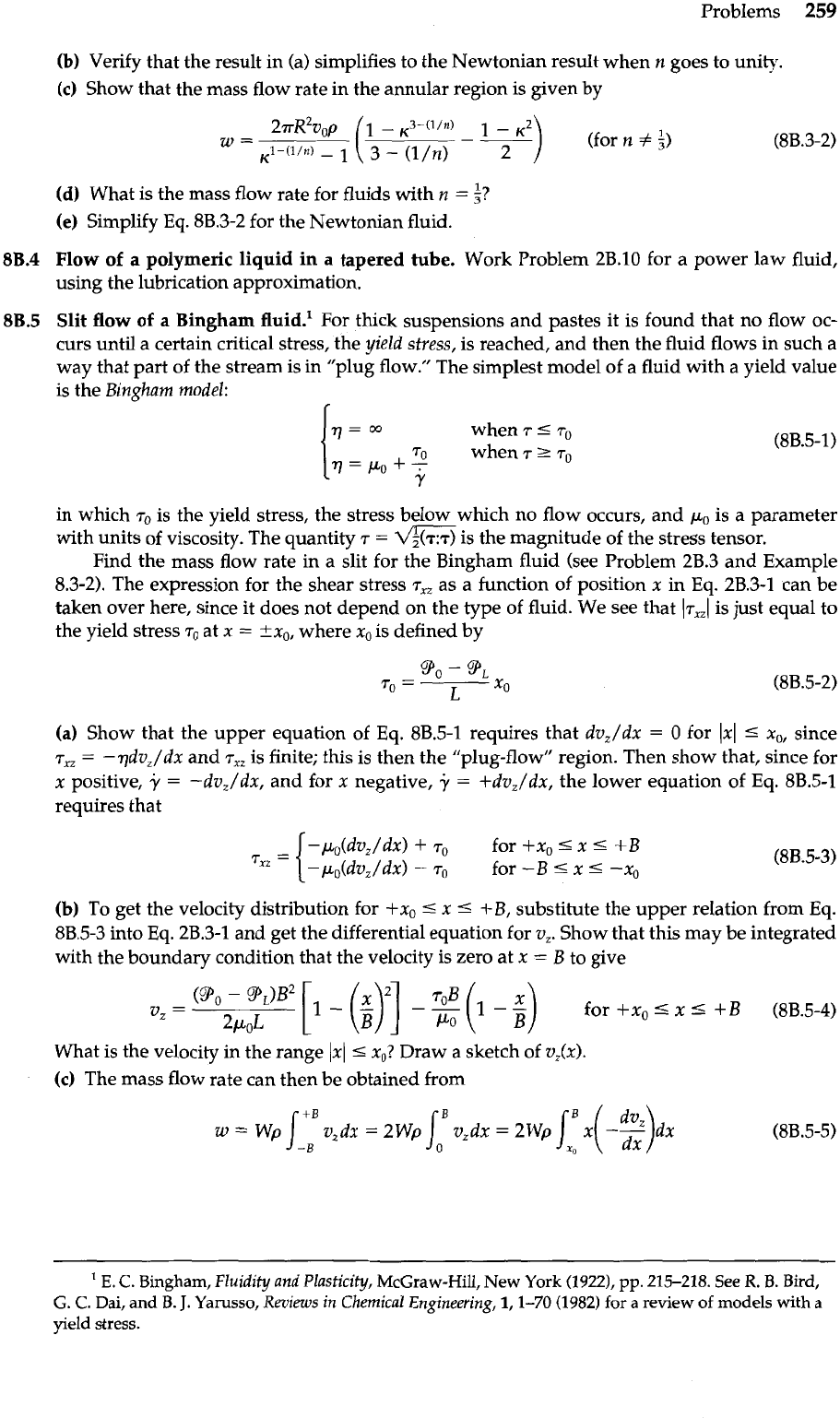
Problems

259

(b)

Verify that the result in (a) simplifies to the Newtonian result when

goes to unity.

(c)

Show that the mass flow rate in the annular region is given by

(dl

What is the mass flow rate for fluids with

(e)

Simplify Eq.

8B.3-2

for the Newtonian fluid.

8B.4 Flow of a polymeric

liquid

a tapered tube.

Work Problem

2B.10

for a power law fluid,

using the lubrication approximation.

88.5

Slit

flow

a Bingham fluid.'

For thick suspensions and pastes it is found that no flow oc-

curs until a certain critical stress, the yield stress, is reached, and then the fluid flows in such a

way that part of the stream is in "plug flow." The simplest model of a fluid with a yield value

is the Bingham model:

when

in which

is the yield stress, the stress below which no flow occurs, and

is a parameter

with units of viscosity. The quantity

is the magnitude of the stress tensor.

Find the mass flow rate in a slit for the Bingham fluid (see Problem

2B.3

and Example

8.3-2).

The expression for the shear stress

r,,

as a function of position x in Eq.

2B.3-1

can be

taken over here, since it does not depend on the type of fluid. We see that

IT,,(

is just equal to

the yield stress

kxo, where xo is defined by

(a)

Show that the upper equation of

Eq.

8B.5-1

requires that dv,/dx

for 1x1

x,, since

rxz

-qdv,/dx and

r,,

is finite; this is then the "plug-flow" region. Then show that, since for

x positive,

-dv,/dx, and for x negative,

+dv,/dx, the lower equation of Eq.

8B.5-1

requires that

-&(dv,/dx)

for +xo

7x2

-p&dv,/dx)

for

-B

-xo

(8B.5-3)

(b)

To get the velocity distribution for +xo

+B, substitute the upper relation from Eq.

8B.5-3

into

Eq.

2B.3-1

and get the differential equation for v,. Show that this may be integrated

with the boundary condition that the velocity is zero at

to give

What is the velocity in the range

1x1

x,? Draw a sketch of v,(x).

(c)

The mass flow rate can then be obtained from

Bingham,

Fluidity and Plasficity,

McGraw-Hill, New

York (19221,

pp.

215-218.

See

Bird,

Dai, and

Yarusso,

Reviews in Chemical Engineering,

1,l-70

(1982) for

review

of models

with

yield stress.

260

Chapter 8 Polymeric Liquids

The integration by parts allows the integration to be done more easily. Show that the

final

result is

Verlfy that, when the yield stress goes to zero, this result simplifies to the Newtonian fluid

result in Problem

2B.3.

Derivation of the Buckingham-Reiner equati~n.~ Rework Example 8.3-1 for the Bingham

model. First find the velocity distribution. Then show that the mass rate of flow is given by

which

(9,

9,)R/2L is the shear stress at the tube wall. This expression is valid only

when

TO.

The complex-viscosity components for

the

Jeffreys fluid.

(a) Work Example 8.4-1 for the Jeffreys model of

Eq.

8.4-4, and show that the results are Eqs.

8.5-12 and

13.

How are these results related to Eqs.

(F)

and

(G)

of Table 8.5-I?

(b) Obtain the complex-viscosity components for the Jeffreys model by using the superposi-

tion suggested in fn.

of s8.4.

Stress relaxation after cessation of shear

flow.

viscoelastic fluid is

steady-state flow

be-

tween a pair of parallel plates, with

yy.

If the flow

suddenly stopped (i.e.,

becomes

zero), the stresses do not go to zero as would be the case for a Newtonian fluid. Explore this

stress

relaxation

phenomenon using a 3-constant Oldroyd model (Eq. 8.5-3 with

0).

(a) Show that in steady-state flow

To what extent does this expression agree with the experimental data in Fig. 8.2-4?

(b) By using Example 8.5-1 (part a) show that, if the flow is stopped at

the shear stress

for

will be

This shows why

is called the "relaxation time." This relaxation of stresses after the

fluid

motion has stopped is characteristic of viscoelastic materials.

7,,

during steady shear flow and after cessation of the flow?

Draining of

tank with an exit pipe (Fig.

78.9).

Rework Problem 7B.9(a) for the power law

fluid.

The Giesekus model.

(a)

Use the results in Table 8.5-1 to get the limiting values for the non-Newtonian viscosity

and the normal stress differences as the shear rate goes to zero.

(b)

Find the limiting expressions for the non-Newtonian viscosity and the two normal-stress

coefficients in the limit as the shear rate becomes infinitely large.

(c)

What

the steady-state elongational viscosity in the limit that the elongation rate tends to

zero? Show that the elongational viscosity has a finite limit as the elongation rate goes to

infinity.

Buckingham,

Proc.

ASTM,

21,115P1161 (1921);

Reiner,

Deformation

and

Flow,

Lewis,

London

(1949).

Problems

261

8C.1

The cone-and-plate viscometer (Fig. 2B.llL3 Review the Newtonian analysis of the cone-

and-plate instrument in Problem 2B.11 and then do the following:

(a) Show that the shear rate

is uniform throughout the gap and equal to

-ye+

il/q0.

Because of the uniformity of y, the components of the stress tensor are also constant through-

out the gap.

(b)

Show that the non-Newtonian viscosity is then obtained from measurements of the

torque

and rotation speed

using

(c)

Show that for the cone-and-plate system the radial component of the equation of mo-

tion is

if the centrifugal force term

-pv$/r

can be neglected. Rearrange this to get

Then introduce the normal stress coefficients, and use the result of (a) to replace

d.lr,,/d

dn-,,/a

to get

Integrate this from

and use the boundary condition

n-JR)

to get

in which

is the atmospheric pressure acting on the fluid at the rim of the cone-and-plate

instrument.

(d)

Show that the total thrust in the

direction exerted by the fluid on the cone

From this one can obtain the first normal-stress coefficient

measuring the force that the

fluid exerts.

(e) Suggest a method for measuring the second normal-stress coefficient using results in part

(c)

if small pressure transducers are flush-mounted in the plate at several different radial loca-

tions.

8C.2

Squeezing flow between parallel disks (Fig. 3C.1): Rework Problem 3C.l(g) for the power

law fluid. This device can be useful for determining the power law parameters for materials

that are highly viscous. Show that the power law analog of Eq. 3C.1-16 is

Bird,

Armstrong, and

Hassager,

Dynamics of Polymeric Liquids,

Vol.

Fluid

Mechanics,

Wiley-Interscience, New York, 2nd Edition

(19871,

pp.

521-524.

Leider,

Ind.

Eng.

Chem. Fundam.,

13,342-346

(1974);

Grimm,

AlChE

Journal,

24,427-439

(1978).

262

Chapter 8 Polymeric Liquids

8C.3

Verification of Giesekus viscosity f~nction.~

(a)

To check the shear-flow entries in Table 8.5-1, introduce dimensionless stress tensor com-

ponents Tij

(A/~,)T~

and a dimensionless shear rate

Aj, and then show that for steady-

state shear flow

Eq.

8.5-4 becomes

a(T;,

q,)

a(T&

Ti!,)

T,,

IT,,

aT,,(T,,

T,)

-I-

There is also a fourth equation, which leads to

T,,

(b) Rewrite these equations in terms of the dimensionless normal-stress differences

Txl

T,,

and

Tyy

T,,,

and

T,,.

(c)

It is difficult to solve the equations in (b) to get the dimensionless shear stress and normal-

stress differences in terms of the dimensionless shear rate. Instead, solve for N,, T,, and

functions of

N,:

(dl Solve the last equation for

as a function of

to get

where

Then get the expression for the non-Newtonian viscosity and plot the curve of

r](y).

8C.4 Tube Flow for the Oldroyd 6-Constant Model. Find the mass flow rate for the steady flow

in a long circular tube6 using

Eq.

8.5-3.

8C.5 Chain Models with Rigid-Rod Connectors. Read and discuss the following publications:

Gottlieb, Computers in Chemisty,

155-160 (1977);

Hassager,

Chem. Phys.,

60,

2111-2124 (1974);

Fan and T. W. Liu,

Non-Newtonian

Fluid

Mech., 19, 303-321 (1986);

Liu,

Chem. Phys., 90, 5826-5842 (1989);

H. H.

Saab, R.

Bird, and

Curtiss,

Chem. Phys., 77, 4758-4766 (1982);

Schieber,

Chem. Phys., 87, 49174927, 49284936

(1987). Why are rodlike connectors more difficult to handle than springs? What kinds of prob-

lems can be solved

computer simulations?

Giesekus,

Non-Newtonian

Fluid

Mech.,

11,69-109 (1982).

Williams and

Bird,

AlClzE

/ouvnal,

8,378-382

(1962).

Part

Two

Energy

Transport

This Page Intentionally Left Blank

Chapter

Thermal Conductivity

and

the

Mechanisms of Energy Transport

Fourieis law of heat conduction (molecular energy transport)

Temperature and pressure dependence of heat conductivity

Theory of thermal conductivity of gases at low density

Theory of thermal conductivity of liquids

Thermal conductivity of solids

Effective thermal conductivity of composite solids

Convective transport

energy

Work associated with molecular motions

It is common knowledge that some materials such as metals conduct heat readily,

whereas others such as wood act as thermal insulators. The physical property that de-

scribes the rate at which heat is conducted is the thermal conductivity

Heat conduction in fluids can be thought of as molecular energy transport, inasmuch

as the basic mechanism is the motion of the constituent molecules. Energy can also be

transported by the bulk motion of a fluid, and this is referred to as convective energy trans-

port; this form of transport depends on the density

of the fluid. Another mechanism is

that of difisive energy transport, which occurs in mixtures that are interdiffusing. In addi-

tion, energy can be transmitted by means of radiative energy transport, which is quite dis-

tinct in that this form of transport does not require a material medium as do conduction

and convection. This chapter introduces the first two mechanisms, conduction and con-

vection. Radiation is treated separately in Chapter

16,

and the subject of diffusive heat

transport arises in 519.3 and again in

g24.2.

We begin in 59.1 with the definition of the thermal conductivity

by Fourier's law

for the heat flux vector

In 59.2 we summarize the temperature and pressure depen-

dence of

for fluids by means of the principle of corresponding states. Then in the next

four sections we present information about thermal conductivities of gases, Liquids,

solids, and solid composites, giving theoretical results when available.

Since in Chapters

and

we will be setting up problems by using the law of con-

servation of energy, we need to know not only how heat moves into and out of a system

but also how work is done on or by a system by means of molecular mechanisms. The na-

ture of the molecular work terms is discussed in 59.8. Finally, by combining the conduc-

tive heat flux, the convective energy flux, and the work flux we can create a combined

energy

flux

vector

which is useful in setting up energy balances.

266

Chapter

Thermal Conductivity and the Mechanisms of Energy Transport

9.1

FOURIER'S LAW OF HEAT

CONDUCTION

(MOLECULAR ENERGY TRANSPORT)

Consider a slab of solid material of area

located between two large parallel plates

distance

apart. We imagine that initially (for time

the solid material is at a tem-

perature

throughout. At

the lower plate is suddenly brought to a slightly higher

temperature

and maintained at that temperature. As time proceeds, the temperature

profile in the slab changes, and ultimately a linear steady-state temperature distribution

is attained (as shown in Fig. 9.1-1). When this steady-state condition has been reached,

constant rate of heat flow

through the slab is required to maintain the temperature dif-

ference

To.

It is found then that for sufficiently small values of

the follow-

ing relation holds:

That is, the rate of heat flow per unit area is proportional to the temperature decrease

over the distance

The constant of proportionality

is the

thermal conductivity

the

slab. Equation 9.1-1 is also valid if a liquid or gas is placed between the two plates, pro-

vided that suitable precautions are taken to eliminate convection and radiation.

In subsequent chapters it is better to work with the above equation in differential

form. That is, we use the limiting form of Eq. 9.1-1 as the slab thickness approaches zero.

The local rate of heat flow per unit area (heat flux) in the positive

direction is desig-

nated by

qy.

In this notation Eq. 9.1-1 becomes

This equation, which serves to define

is the one-dimensional form of

Fourier's

law

heat cond~ction.',~

It states that the heat flux by conduction is proportional to the tempera-

Solid initially at

temperature

Lower plate

suddenly raised

temperature

Small

Large

T(y)

Fig.

9.1-1.

Development of the

steady-state temperature pro-

file for a solid slab between two

parallel plates. See

Fig.

1.1-1 for

the analogous situation for mo-

mentum transport.