Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


Problems
227
I
PI
l
I
Plane
1
I
p2
I
I
Plane
2
Fig.
7B.5.
Installation of an air duct.
7B.6
Multiple discharge into a common conduip (Fig.
7B.6).
Extend Example
7.6-1
to an incom-
pressible fluid discharging from several tubes into a larger tube with a net increase in cross
section. Such systems are important in heat exchangers of certain types, for which the expan-
sion and contraction losses account for an appreciable fraction of the overall pressure drop.
The flows in the small tubes and the large tube may be laminar or turbulent. Analyze this sys-
tem by means of the macroscopic mass, momentum, and mechanical energy balances.
Plane
1
,,
Plane
2
Fig.
7B.6.
Multiple discharge into a
common conduit. The total cross sec-
tional area at plane
1
available for
flow is
S,
and that at plane
2
is
S,.
7B.7
Inventory variations in a gas reservoir.
A
natural gas reservoir is to be supplied from a
pipeline at a steady rate of
w,
lbm/hr. During a 24-hour period, the fuel demand from the
reservoir, w,, varies approximately as follows,
w2
=
A
+
B
cos
ot
(7B.7-1)
where
wt
is a dimensionless time measured from the time of peak demand (approximately
6
A.M.).
(a) Determine the maximum, minimum, and average values of w2 for a 24-hour period in
terms of A and
B.
(b)
Determine the required value of
w,
in terms of A and
B.
(c)
Let
m,,,
=
m!,,
at
t
=
0, and integrate the unsteady mass balance with this initial condition
to obtain
m,,,
as a function of time.
(d)
If A
=
5000 lbm/hr,
B
=
2000 Ibm/hr, and
p
=
0.044 lb,,,/ft3 in the reservoir, determine the
absolute minimum reservoir capacity in cubic feet to meet the demand without interruption.
At what time of day must the reservoir be full to permit such operation?
(e)
Determine the minimum reservoir capacity in cubic feet required to permit maintaining at
least a three-day reserve at all times.
Answer:
3.47
X
lo5
ft3;
8.53
X
lo6
ft3
W.
M.
Kays,
Trans.
ASME,
72,1067-1074 (1950).
228
Chapter 7 Macroscopic Balances for Isothermal Flow Systems
Change in liquid height with time (Fig. 7.1-1).
(a) Derive Eq. 7.1-4 by using integral calculus.
(b) In Example 7.1-1, obtain the expression for the liquid height
h
as a function of time
t.
(c) Make a graph of Eq. 7.1-8 using dimensionless quantities. Is this useful?
Draining of
a
cylindrical tank with exit pipe (Fig. 7B.9).
(a) Rework Example 7.1-1, but with a cylindrical tank instead of a spherical tank. Use
the
quasi-steady-state approach; that is, use the unsteady-state mass balance along with the
Hagen-Poiseuille equation for the laminar flow in the pipe.
(b) Rework the problem for turbulent flow in the pipe.
Answer:
(a)
tefflux
=
Fig.
7B.9.
A
cylindrical tank with a long pipe attached. The fluid surface
and pipe exit are open to the atmosphere.
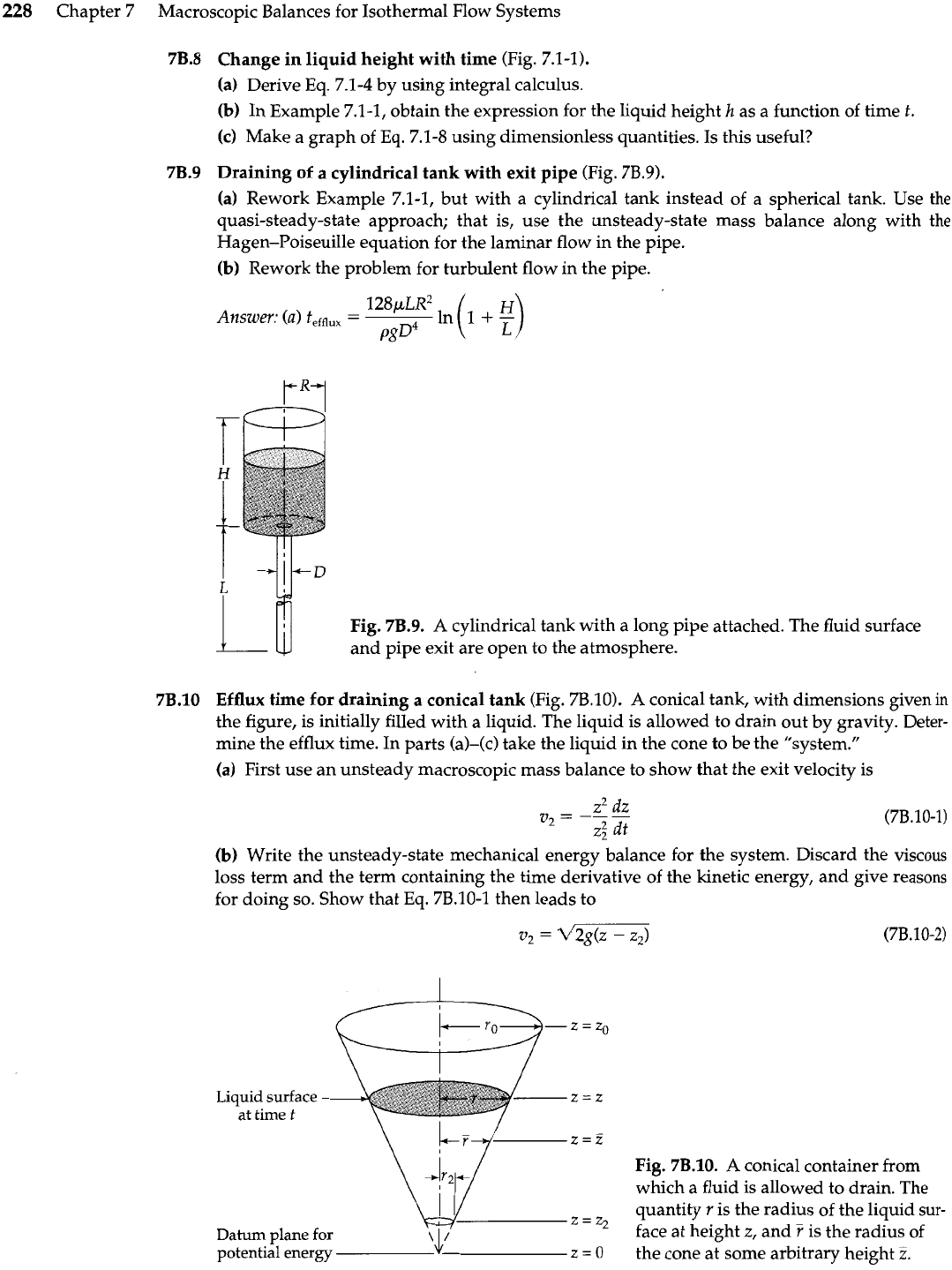
Efflux time for draining a conical tank (Fig. 7J3.10).
A
conical tank, with dimensions given
in
the figure, is initially filled with a liquid. The liquid is allowed to drain out
by
gravity. Deter-
mine the efflux time. In parts (a)-(c) take the liquid in the cone to be the "system."
(a) First use an unsteady macroscopic mass balance to show that the exit velocity is
(b) Write the unsteady-state mechanical energy balance for the system. Discard the viscous
loss term and the term containing the time derivative of the kinetic energy, and give reasons
for doing so. Show that
Eq.
7B.10-1 then leads to
Liquid surface
z=z
at time
t
z=Z
Fig.
7B.10.
A
conical container from
which a fluid is allowed to drain. The
Datum plane for
Z
=
Z2
quantity
r
is the radius of the liquid sur-
\I
/
face at height
z,
and
F
is the radius of
potential energy
\L
z
=
0
the cone at some arbitrary height
Z.
Problems
229
(c)
Combine the results of (a) and (b). Solve the resulting differential equation with an appro-
priate initial condition to get the liquid level
z
as a function of
t.
From this get the efflux time
List all the assumptions that have been made and discuss how serious they are. How could
these assumptions be avoided?
(d) Rework part (b) by choosing plane 1 to be stationary and slightly below the liquid surface
at time t. It is understood that the liquid surface does not go below plane
1
during the differ-
ential time interval dt over which the unsteady mechanical energy balance is made. With this
choice of plane 1 the derivative d@,,,/dt is zero and there is no work term
W,.
Furthermore
the conditions at plane
1
are very nearly those at the liquid surface. Then with the pseudo-
steady-state approximation that the derivative dK,,,/dt is approximately zero and the neglect
of the viscous loss term, the mechanical energy balance, with w,
=
w,, takes the form
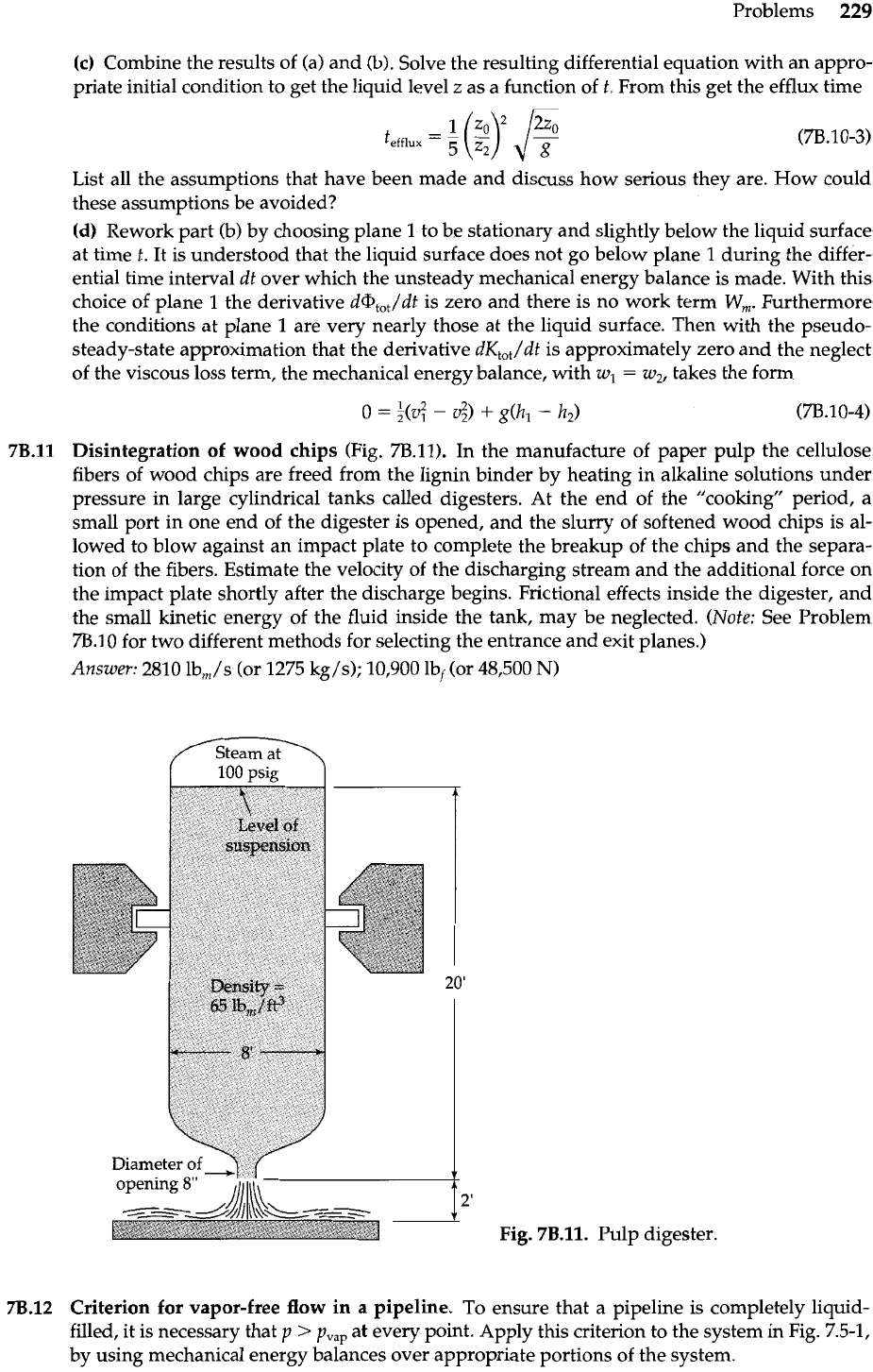
7B.11
Disintegration of wood chips (Fig. 7B.11). In the manufacture of paper pulp the cellulose
fibers of wood chips are freed from the lignin binder by heating in alkaline solutions under
pressure in large cylindrical tanks called digesters. At the end of the "cooking" period, a
small port in one end of the digester is opened, and the slurry of softened wood chips is al-
lowed to blow against an impact plate to complete the breakup of the chips and the separa-
tion of the fibers. Estimate the velocity of the discharging stream and the additional force on
the impact plate shortly after the discharge begins. Frictional effects inside the digester, and
the small kinetic energy of the fluid inside the tank, may be neglected. (Note: See Problem
7B.10 for two different methods for selecting the entrance and exit planes.)
Answer: 2810 lb,/s (or 1275 kg/$; 10,900 lbf (or 48,500
N)
Diameter
of
-7
(
Fig.
7B.11.
Pulp digester.
7B.12
Criterion for vapor-free flow
in
a
pipeline. To ensure that a pipeline is completely liquid-
filled, it is necessary that
p
>
p,,,
at every point. Apply this criterion to the system in Fig. 7.5-1,
by using mechanical energy balances over appropriate portions of the system.

230
Chapter
7
Macroscopic Balances for Isothermal Flow Systems
7C.1 End corrections in tube viscometers (Fig.
7C.1L3
In analyzing tube-flow viscometric data
to
determine viscosity, one compares pressure drop versus flow rate data with the theoretical
expression (the Hagen-Poiseuille equation of Eq.
2.3-21).
The latter assumes that the flow
is
fully developed in the region between the two planes at which the pressure is measured.
In
an apparatus such as that shown
in
the figure, the pressure is known at the tube exit
(2)
and
also above the fluid in the reservoir
(1).
However, in the entrance region of the tube,
the
velocity profiles are not yet fully developed. Hence the theoretical expression relating
the
pressure drop to the flow rate is not valid.
There is, however, a method in which the Hagen-Poiseuille equation can be used,
by
making flow measurements in two tubes of different lengths,
LA
and
LB;
the shorter of the
two
tubes must be long enough so that the velocity profiles are fully developed at the exit. Then
the end section of the long tube, of length
L,
-
LA,
will be a region of fully developed flow.
If
we knew the value of
Po
-
9,
for this region, then we could apply the Hagen-Poiseuille
equation.
Show that proper combination of the mechanical energy balances, written for the sys-
tems
1-2,34,
and
04
gives the following expression for
9,
-
9,
when each viscometer has
the
same
flow
rate.
where
60
=
po
+
pgz,.
Explain carefully how you would use
Eq.
7C.1-1
to analyze experimen-
tal measurements. Is Eq.
7C.1-1
valid for ducts with noncircular, uniform cross section?
Run
A
Run
B
Plane
3
Fig.
7C.1. Two tube viscometers with
the same flow rate and the same exit
pressure. The pressures
pA
and
pB
are
Plane
4
maintained by an inert gas.
7D.1 Derivation of the macroscopic balances from the equations of change. Derive the macro-
scopic mass and momentum balances by integrating the equations of continuity and motion
over the flow system of Fig.
7.0-1.
Follow the procedure given in
97.8
for the macroscopic me-
chanical energy balance, using the Gauss divergence theorem and the Leibniz formula.
A.
G.
Fredrickson, PhD Thesis, University
of
Wisconsin (1959);
Principles and Applications
of
Rheology,
Prentice-Hall, Englewood Cliffs,
N.J.
(1964),
59.2.

Chapter
8
Polymeric
Liquids
8.1
Examples of the behavior of polymeric liquids
98.2 Rheometry and material functions
58.3 Non-Newtonian viscosity and the generalized Newtonian models
58.4'
Elasticity and the linear viscoelastic models
58.5.
The corotational derivatives and the nonlinear viscoelastic models
58.6.
Molecular theories for polymeric liquids
In the first seven chapters we have considered only Newtonian fluids. The relations be-
tween stresses and velocity gradients are described by Eq. 1.1-2 for simple shear flow
and by Eq. 1.2-6 (or
Eq.
1.2-7) for arbitrary time-dependent flows. For the Newtonian
fluid, two material parameters are needed-the two coefficients of viscosity
p
and
K-
which depend on temperature, pressure, and composition, but not on the velocity gradi-
ents. All gases and all liquids composed of "small" molecules (up to molecular weights
of about
5000)
are accurately described by the Newtonian fluid model.
There are many fluids that are not described by Eq. 1.2-6, and these are called non-
Newtonian fluids. These structurally complex fluids include polymer solutions, polymer
melts, soap solutions, suspensions, emulsions, pastes, and some biological fluids. In this
chapter we focus on polymeric liquids.
Because they contain high-molecular-weight molecules with many internal degrees
of freedom, polymer solutions and molten polymers have behavior qualitatively differ-
ent from that of Newtonian fluids. Their viscosities depend strongly on the velocity gra-
dients, and in addition they may display pronounced "elastic effects." Also in the steady
simple shear flow between two parallel plates, there are nonzero and unequal normal
stresses
(rxx, rYY,
and
T,,)
that do not arise in Newtonian fluids. In 58.1 we describe some
experiments that emphasize the differences between Newtonian and polymeric fluids.
In dealing with Newtonian fluids the science of the measurement of viscosity is
called viscomety, and in earlier chapters we have seen examples of simple flow systems
that can be used as viscometers (the circular tube, the coneplate system, and coaxial cylin-
ders). To characterize non-Newtonian fluids we have to measure not only the viscosity,
but the normal stresses
and the viscoelastic responses as well. The science of
measurement of these properties is called rheometry, and the instruments are called
rheometers. We treat this subject briefly in 58.2. The science of rheology includes all aspects
of the study of deformation and flow of non-Hookean solids and non-Newtonian liquids.
After the first two sections, which deal with experimental facts, we turn to the pre-
sentation of various non-Newtonian "models" (that is, empirical expressions for the
stress tensor) that are commonly used for describing polymeric liquids. In 58.3 we start
with the generalized Newtonian models, which are relatively simple, but which can describe
only the non-Newtonian viscosity (and not the viscoelastic effects). Then in s8.4 we give
examples of linear viscoelastic models, which can describe the viscoelastic responses, but

232
Chapter
8
Polymeric Liquids
only in flows with exceedingly small displacement gradients. Next
in
s8.5 we give several
nonlinear viscoelastic models, and these are intended to be applicable
in
all flow situations.
As we go from elementary to more complicated models, we enlarge the set of observed
phenomena that we can describe (but also the mathematical difficulties). Finally in
58.6
there is a brief discussion about the kinetic theory approach to polymer fluid dynamics.
Polymeric liquids are encountered in the fabrication of plastic objects, and as addi-
tives to lubricants, foodstuffs, and inks. They represent a vast and important class of
liq-
uids, and many scientists and engineers must deal with them. Polymer fluid dynamics,
heat transfer, and diffusion form a rapidly growing part of the subject of transport phe-
nomena, and there are many textbooks,' treatises; and journals devoted to the subject.
The subject has also been approached from the kinetic theory standpoint, and molecular
theories of the subject have contributed much to our understanding of the mechanical,
thermal, and diffusional behavior of these fluids3 Finally, for those interested in the his-
tory of the subject, the reader is referred to the book by Tanner and Waltem4
8.1
EXAMPLES OF THE BEHAVIOR OF POLYMERIC LIQUIDS
In this section we discuss several experiments that contrast the flow behavior of New-
tonian and polymeric fluids.'
Steady-State Laminar Flow in Circular
Tubes
Even for the steady-state, axial, laminar flow in circular tubes, there is an important dif-
ference between the behavior of Newtonian liquids and that of polymeric liquids.
For
Newtonian liquids the velocity distribution, average velocity, and pressure drop
are
given by Eqs. 2.3-18,2.3-20, and 2.3-21, respectively.
For polymeric liquids, experimental data suggest that the following equations
are
reasonable:
where
n
is a positive parameter characterizing the fluid, usually with a value less than
unity. That is, the velocity profile is more blunt than it is for the Newtonian fluid,
for
which n
=
1. It is further found experimentally that
The pressure drop thus increases much less rapidly with the mass flow rate than
for
Newtonian fluids, for which the relation is linear.
A.
S. Lodge,
Elastic Liquids,
Academic Press, New York (1964);
R.
B. Bird,
R.
C. Armstrong, and
0.
Hassager,
Dynamics of Polymeric Liquids, Vol.
1
.,
Fluid Mechanics,
Wiley-Interscience, New York, 2nd
edition (1987);
R.
I. Tanner,
Engineering Rheology,
Clarendon Press, Oxford (1985).
H.
A. Barnes,
J.
F
Hutton, and
K.
Walters,
An Introduction to Rheology,
Elsevier, Amsterdam (1989);
H.
Giesekus,
Phanomenologische Rheologie: Eine Einfiihrung,
Springer Verlag, Berlin (1994). Books
emphasizing the engineering aspects of the subject include
Z.
Tadmor and
C.
G.
Gogos,
Principles of
Polymer Processing,
Wiley, New York (1979), D. G. Baird and D. I. Collias,
Polymer Processing: Principles
and Design,
Butterworth-Heinemann, Boston (1995),
J.
Dealy and
K.
Wissbrun,
Melt Rheology and its RoIe
in Plastics Processing,
Van Nostrand Reinhold, New York (1990).
R.
B.
Bird, C.
F.
Curtiss,
R.
C. Armstrong, and
0.
Hassager,
Dynamics of Polymeric Liquids, Vol.
2,
Kinetic Theoy,
Wiley-Interscience, New York, 2nd edition (1987); C.
F.
Curtiss and
R.
B.
Bird,
Adv.
Polymer Sci,
125,l-101 (1996) and
J.
Chem. Phys.
111,10362-10370 (1999).
R.
I.
Tanner and
K.
Walters,
Rheology: An Historical Perspective,
Elsevier, Amsterdam (1998).
More details about these and other experiments can be found in
R.
B.
Bird,
R.
C.
Armstrong, and
0.
Hassager,
Dynamics of Polymeric Liquids, Vol.
1,
Fluid Dynamics,
Wiley-Interscience, New York,
2nd
edition
(1987), Chapter 2. See also A. S. Lodge,
Elastic Liquids,
Academic Press, New York
(19641,
Chapter 10.
8.1
Examples of the Behavior of Polymeric Liquids
233
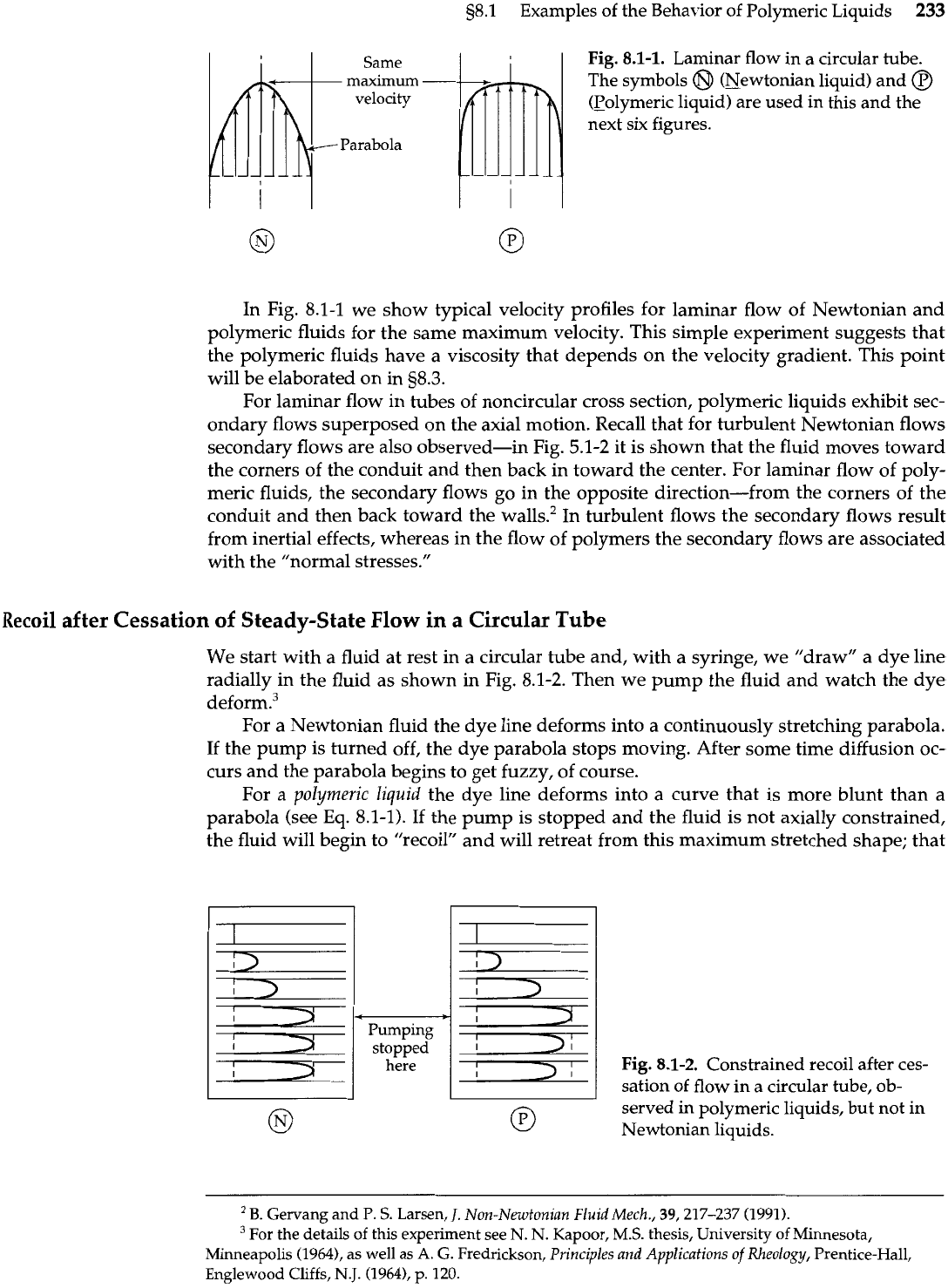
Fig.
8.1-1.
Laminar flow in a circular tube.
The symbols
@
(Newtonian liquid) and
@
(polymeric liquid) are used in this and the
next six figures.
In Fig. 8.1-1 we show typical velocity profiles for laminar flow of Newtonian and
polymeric fluids for the same maximum velocity. This simple experiment suggests that
the polymeric fluids have a viscosity that depends on the velocity gradient. This point
will be elaborated on in s8.3.
For laminar flow in tubes of noncircular cross section, polymeric liquids exhibit sec-
ondary flows superposed on the axial motion. Recall that for turbulent Newtonian flows
secondary flows are also observed-in Fig.
5.1-2
it is shown that the fluid moves toward
the corners of the conduit and then back in toward the center. For laminar flow of poly-
meric fluids, the secondary flows go in the opposite direction-from the corners of the
conduit and then back toward the walls.' In turbulent flows the secondary flows result
from inertial effects, whereas in the flow of polymers the secondary flows are associated
with the "normal stresses."
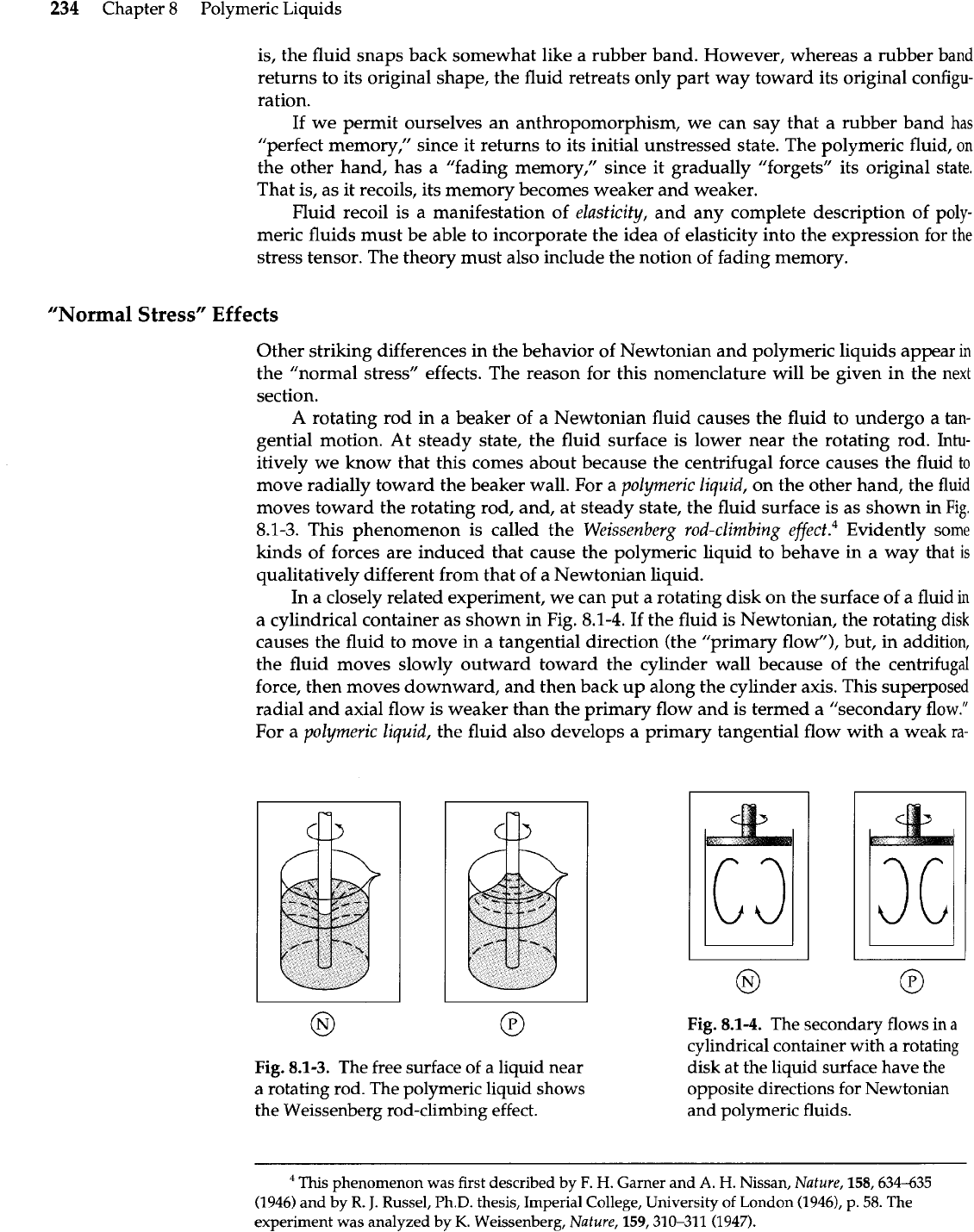
Recoil after Cessation of Steady-State Flow in a Circular Tube
We start with a fluid at rest in a circular tube and, with a syringe, we "draw" a dye line
radially in the fluid as shown in Fig.
8.1-2.
Then we pump the fluid and watch the dye
def~rrn.~
For a Newtonian fluid the dye line deforms into a continuously stretching parabola.
If the pump is turned off, the dye parabola stops moving. After some time diffusion oc-
curs and the parabola begins to get fuzzy, of course.
For a
polymeric
liquid
the dye line deforms into a curve that is more blunt than a
parabola (see
Eq.
8.1-1). If the pump is stopped and the fluid is not axially constrained,
the fluid will begin to "recoil" and will retreat from this maximum stretched shape; that
-
Pumping
stopped
here
Fig.
8.1-2.
Constrained recoil after ces-
sation of flow in a circular tube, ob-
served
in
polymeric liquids, but not in
Newtonian liquids.
B.
Gervang and P.
S.
Larsen,
J.
Non-Newtonian Fluid
Mech.,
39,217-237 (1991).
For the details of this experiment see
N. N.
Kapoor,
M.S.
thesis, University of Minnesota,
Minneapolis (1964), as well as
A.
G.
Fredrickson,
Principles and Applications of Rheology,
Prentice-Hall,
Englewood Cliffs,
N.J.
(1964),
p.
120.
234
Chapter
8
Polymeric Liquids
is, the fluid snaps back somewhat like a rubber band. However, whereas a rubber band
returns to its original shape, the fluid retreats only part way toward its original configu-
ration.
If we permit ourselves an anthropomorphism, we can say that a rubber band has
"perfect memory," since it returns to its initial unstressed state. The polymeric fluid,
on
the other hand, has a "fading memory," since it gradually "forgets" its original state.
That is, as it recoils, its memory becomes weaker and weaker.
Fluid recoil is a manifestation of elasticity, and any complete description of poly-
meric fluids must be able to incorporate the idea of elasticity into the expression for
the
stress tensor. The theory must also include the notion of fading memory.
"Normal
Stress" Effects
Other striking differences in the behavior of Newtonian and polymeric liquids appear
in
the "normal stress" effects. The reason for this nomenclature will be given in the next
section.
A rotating rod in a beaker of a Newtonian fluid causes the fluid to undergo a tan-
gential motion. At steady state, the fluid surface is lower near the rotating rod. Intu-
itively we know that this comes about because the centrifugal force causes the fluid
to
move radially toward the beaker wall. For a polymeric liquid, on the other hand, the
fluid
moves toward the rotating rod, and, at steady state, the fluid surface is as shown in
Fig.
8.1-3.
This phenomenon is called the Weissenberg rod-climbing effect.4 Evidently some
kinds of forces are induced that cause the polymeric liquid to behave in a way that
is
qualitatively different from that of a Newtonian liquid.
In a closely related experiment, we can put a rotating disk on the surface of a fluid
in
a cylindrical container as shown in Fig.
8.1-4.
If the fluid is Newtonian, the rotating
disk
causes the fluid to move
in
a tangential direction (the "primary flow"), but, in addition,
the fluid moves slowly outward toward the cylinder wall because of the centrifugal
force, then moves downward, and then back up along the cylinder axis. This superposed
radial and axial flow is weaker than the primary flow and is termed a "secondary flow."
For a polymeric liquid, the fluid also develops a primary tangential flow with a weak ra-
Fig.
8.1-3.
The free surface of a liquid near
a rotating rod. The polymeric liquid shows
opposite directions for Newtonian
the Weissenberg rod-climbing effect. and polymeric fluids.
Fig.
8.1-4.
The secondary flows in
a
cylindrical container with a rotating
disk at the liquid surface have the
This phenomenon was first described by
F.
H.
Garner and
A.
H.
Nissan,
Nature,
158,634-635
(1946) and by R.
J.
Russel, Ph.D. thesis, Imperial College, University of London (1946),
p.
58.
The
experiment was analyzed by
K.
Weissenberg,
Nature,
159,310-311 (1947).

8.1
Examples of the Behavior of Polymeric Liquids
235
Fig.
8.1-5.
Flow down a tilted semicylindri-
)
cal trough. The convexity of the polymeric
dial and axial secondary flow, but the latter goes in a direction opposite to that seen in
the Newtonian fluid.5
In another experiment we can let a liquid flow down a tilted, semi-cylindrical
trough as shown in Fig. 8.1-5. If the fluid is Newtonian, the liquid surface is flat, except
for the meniscus effects at the outer edges. For most polymeric liquids, however, the liquid
surface is found to be slightly convex. The effect is small but repr~ducible.~
Some
Other
Experiments
The operation of a simple siphon is familiar to everyone. We know from experience that,
if the fluid is Newtonian, the removal of the siphon tube from the liquid means that the
siphoning action ceases. However, as may be seen in Fig. 8.1-6, for polymeric liquids the
siphoning can continue even when the siphon
is
lifted several centimeters above the liq-
uid surface. This is called the tubeless
siphon
effect. One can also just lift some of the fluid
up over the edge of the beaker and then the fluid will flow upward along the inside of
the beaker and then down the outside until the beaker is nearly empty.7
In another experiment a long cylindrical rod, with its axis in the
z
direction, is made
to oscillate back and forth in the
x
direction with the axis parallel to the
z
axis (see Fig.
Fig.
8.1-6.
Siphoning continues to occur
when the tube is raised above the surface
of a polymeric liquid,
but
not
so
for
a
-
\
Newtonian liquid. Note the swelling of
@
"Extrudate
the polymeric liquid as it leaves the
swell"
siphon tube.
C.
T. Hill,
J.
D.
Huppler, and
R.
B. Bird,
Chem. Eng. Sci.
21,815-817 (1966);
C.
T. Hill,
Trans. Soc.
Rheol.,
16,213-245 (1972).
Theoretical analyses have been given by
J.
M.
Kramer and
M.
W.
Johnson, Jr.,
Trans. Soc. Rheol.
16,197-212 (1972),
and by
J.
P.
Nirschl and
W.
E. Stewart,
J.
Non-Newtonian Fluid Mech.,
16,233-250 (1984).
This experiment was first done by
R.
I.
Tanner,
Trans. Soc. Rheol.,
14,483-507 (19701,
prompted by
a suggestion
by
A.
S.
Wineman and
A.
C.
Pipkin,
Acta Mech.
2,104-115
(1966).
See also
R.
I. Tanner,
Engineering Rheology,
Oxford University Press
(1985), 102-105.
D.
F. James,
Nature,
212,754-756 (1966).
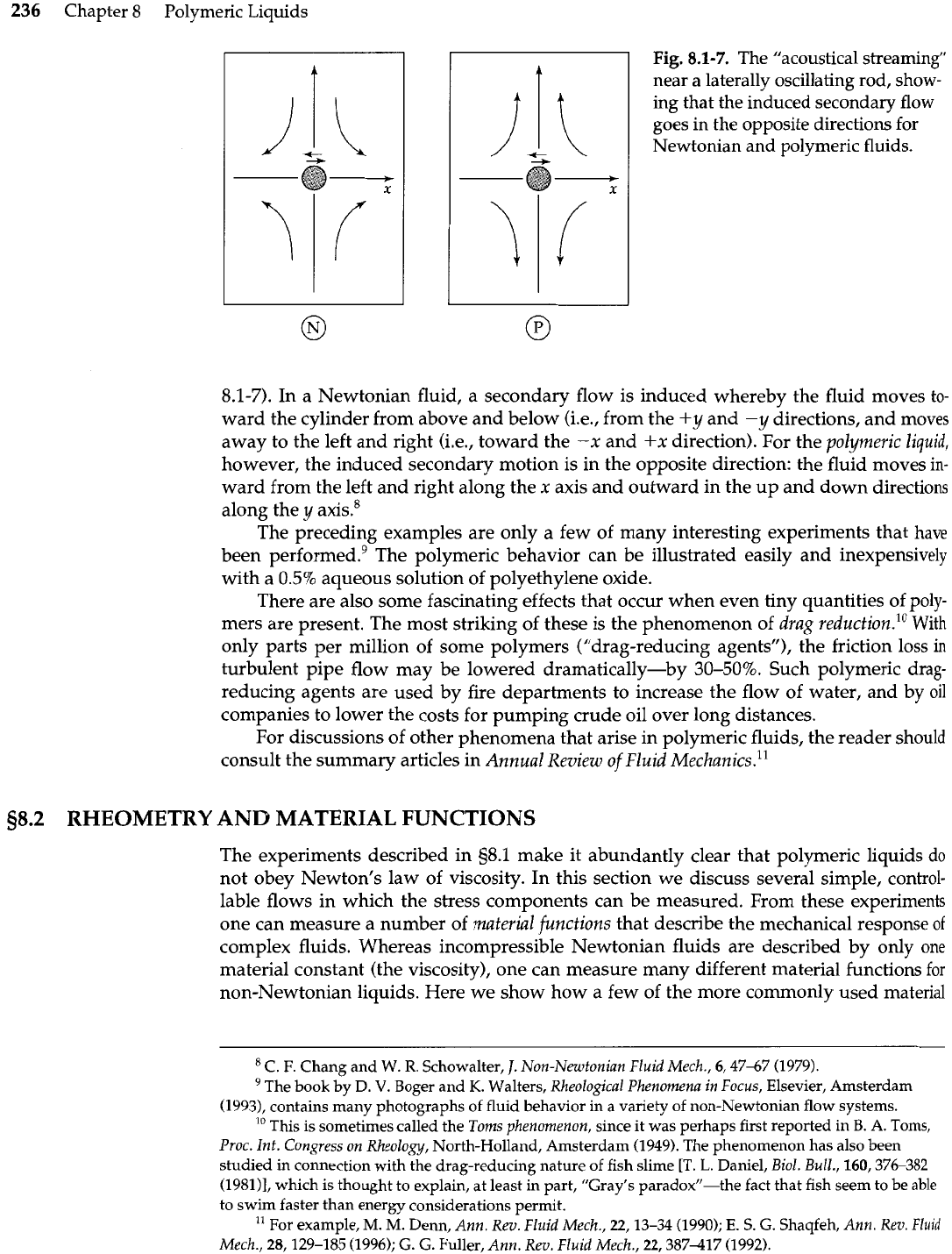
236
Chapter
8
Polymeric Liquids
Fig.
8.1-7.
The "acoustical streaming"
near a laterally oscillating rod, show-
ing that the induced secondary flow
goes in the opposite directions for
Newtonian and polymeric fluids.
8.1-7). In a Newtonian fluid, a secondary flow is induced whereby the fluid moves to-
ward the cylinder from above and below (i.e., from the
+y
and
-y
directions, and moves
away to the left and right (i.e., toward the
-x
and
+x
direction). For the
polymeric liquid,
however, the induced secondary motion is in the opposite direction: the fluid moves in-
ward from the left and right along the
x
axis and outward in the up and down directions
along the
y
axk8
The preceding examples are only a few of many interesting experiments that
have
been performed.9 The polymeric behavior can be illustrated easily and inexpensively
with a
0.5%
aqueous solution of polyethylene oxide.
There are also some fascinating effects that occur when even tiny quantities of poly-
mers are present. The most striking of these is the phenomenon of
drag reduction.1°
With
only parts per million of some polymers ("drag-reducing agents"), the friction loss
in
turbulent pipe flow may be lowered dramatically-by
30-50%.
Such polymeric drag-
reducing agents are used by fire departments to increase the flow of water, and by
oil
companies to lower the costs for pumping crude oil over long distances.
For discussions of other phenomena that arise in polymeric fluids, the reader should
consult the summary articles in
Annual Review of
Fluid
~echanics.~'
98.2
RHEOMETRY AND MATERIAL FUNCTIONS
The experiments described in 38.1 make it abundantly clear that polymeric liquids do
not obey Newton's law of viscosity. In this section we discuss several simple, control-
lable flows in which the stress components can be measured. From these experiments
one can measure a number of
material functions
that describe the mechanical response
of
complex fluids. Whereas incompressible Newtonian fluids are described by only one
material constant (the viscosity), one can measure many different material functions
for
non-Newtonian liquids. Here we show how a few of the more commonly used material
C.
F.
Chang and W.
R.
Schowalter,
J.
Non-Newtonian Fluid Mech.,
6,4747 (1979).
The book by
D.
V.
Boger and
K.
Walters,
Rheological Phenomena in Focus,
Elsevier, Amsterdam
(1993),
contains many photographs of fluid behavior in a variety of non-Newtonian flow systems.
'O
This is sometimes called the
Toms phenomenon,
since it was perhaps first reported in
B.
A. Toms,
Proc.
Int.
Congress on Rheology,
North-Holland, Amsterdam
(1949).
The phenomenon has also been
studied
in
connection with the drag-reducing nature
of
fish slime
[T.
L.
Daniel,
Biol. Bull.,
160,376-382
(1981)],
which is thought to explain, at least in part, "Gray's paradoxu-the fact that fish seem to be
able
to swim faster than energy considerations permit.
"
For example,
M. M.
Denn,
Ann. Rev. Fluid Mech.,
22,1334 (1990);
E.
S.
G.
Shaqfeh,
Ann. Rev.
Fluid
Mech.,
28,129-185 (1996);
G.
G.
Fuller,
Ann. Rev. Fluid Mech.,
22,387417 (1992).
