Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


58.2
Rheometry and Material Functions
237
functions are defined and measured. Information about the actual measurement equip-
ment and other material functions can be found e1sewhere.l~~ It is assumed throughout
this chapter that the polymeric liquids can be regarded as incompressible.
Steady
Simple Shear Flow
We consider now the steady shear flow between a pair of parallel plates, where the ve-
locity profile is given by vx
=
jy,
the other velocity components being zero (see Fig. 8.2-
1). The quantity y, here taken to be positive, is called the "shear rate." For a Newtonian
fluid the shear stress
ryx
is given by Eq. 1.1-2, and the normal stresses
(rxx,
r,,, and
r,,)
are
all zero.
For incompressible non-Newtonian fluids, the normal stresses are nonzero and un-
equal. For these fluids it is conventional to define three material functions as follows:
in which 7 is the non-Newtonian viscosity,
q1
is the first normal stress coefficient, and
q2
is the second normal stress coefficient. These three quantities-7,
TI,
q2-are all
functions of the shear rate
y.
For many polymeric liquids q may decrease by a factor of
as much as
lo4
as the shear rate increases. Similarly, the normal stress coefficients may
decrease by a factor of as much as
lo7
over the usual range of shear rates. For polymeric
fluids made up of flexible macromolecules, the functions q(
j)
and q,(y) have been found
experimentally to be positive, whereas !P,(y) is almost always negative. It can be shown
that for positive
TI($
the fluid behaves as though it were under tension in the flow (or
X)
direction, and that the negative !P,(y) means that the fluid is under tension in the
transverse (or
z)
direction. For the Newtonian fluid 7
=
p,
V,
=
0, and
q2
=
0.
The strongly shear-ratedependent non-Newtonian viscosity is connected with the
behavior given in Eqs. 8.1-1 to 3, as is shown in the next section. The positive
9,
is pri-
marily responsible for the Weissenberg rod-climbing effect. Because of the tangential
flow, there is a tension in the tangential direction, and this tension pulls the fluid toward
the rotating rod, overcoming the centrifugal force. The secondary flows in the disk-and-
cylinder experiment (Fig. 8.1-4) can also be explained qualitatively in terms of the posi-
tive !PI. Also, the negative !P2 can be shown to explain the convex surface shape in the
tilted-trough experiment (Fig. 8.1-5).
Uvver date moves at
a
constant meed
II
I
I
t
Fig.
8.2-1.
Steady simple shear flow be-
I
tween parallel plates, with shear rate
j.
!d
For Newtonian fluids in this flow,
r,,
=
-
,,..
;,
=
yy
ryy
=
r,,
=
0,
but for polymeric fluids the
normal stresses are in general nonzero
and unequal.
'
J.
R.
Van
Wazer,
J.
W. Lyons,
K.
Y. Kim,
and
R.
E.
Colwell,
Viscosity and Flow Measurement,
Interscience (Wiley), New York (1963).
K.
Walters,
Rheometry,
Wiley, New York (1975).

238
Chapter 8 Polymeric Liquids
C-
Upper plate oscillates
with
+
Fig.
8.2-2.
Small-amplitude oscillatory
motion. For small plate spacing and
highly viscous fluids, the velocity pro-
vJy,
t) =
jloy
cos
ot
file may be assumed to be linear.
Many ingenious devices have been developed to measure the three material func-
tions for steady shearing flow, and the theories needed for the use of the instruments are
explained in detail el~ewhere.~ See Problem
8C.1
for the use of the cone-and-plate instru-
ment for measuring the material functions.
Small-Amplitude Oscillatory Motion
A
standard method for measuring the elastic response of a fluid is the small-amplitude
oscillatory shear experiment, depicted in Fig.
8.2-2.
Here the top plate moves back and
forth in sinusoidal fashion, and with a tiny amplitude. If the plate spacing is extremely
small and the fluid has a very high viscosity, then the velocity profile will be nearly
lin-
ear, so that
v,(y,
t)
=
joy cos ot, in which
jO,
a real quantity, gives the amplitude of the
shear rate excursion.
The shear stress required to maintain the oscillatory motion will also be periodic
in
time and, in general, of the form
T~~
=
-
q' yo
cos
of
-
q"jO sin wt
(8.2-4)
in which
77'
and q" are the components of the complex viscosity, q*
=
q'
-
iq", which is
a
function of the frequency. The first (in-phase) term is the "viscous response," and
the
second (out-of-phase) term is the "elastic response." Polymer chemists use the curves
of
q'(w) and q"(o) (or the storage and loss moduli,
G'
=
q"w and
G
=
q'o) for "characteriz-
ing" polymers, since much is known about the connection between the shapes of these
curves and the chemical str~cture.~ For the Newtonian fluid, q'
=
p
and
77''
=
0.
Steady-State Elongational Flow
A
third experiment that can be performed involves the stretching of the fluid, in which
the velocity distribution is given by
v,
=
I:z,
v,
=
-$Ex,
and
vy
=
-$4y
(see Fig. 8.2-31,
where the positive quantity
I:
is called the "elongation rate." Then the relation
defines the elongational viscosity
7,
which depends on
I:.
When
I:
is negative, the flow
is
referred to as biaxial stretching. For the Newtonian fluid it can be shown that
7
=
3p,
and
this is sometimes called the "Trouton viscosity."
<
Fig.
8.2-3.
Steady elongational
flow
1. 1.
vZ=EZ, vx=--EX,
v
=--EY
2
Y
2
with elongation rate
E
=
dv,/dz.
J.
D.
Ferry,
Viscoelastic
Properties
of
Polymers,
Wiley,
New
York, 3rd edition
(1980).
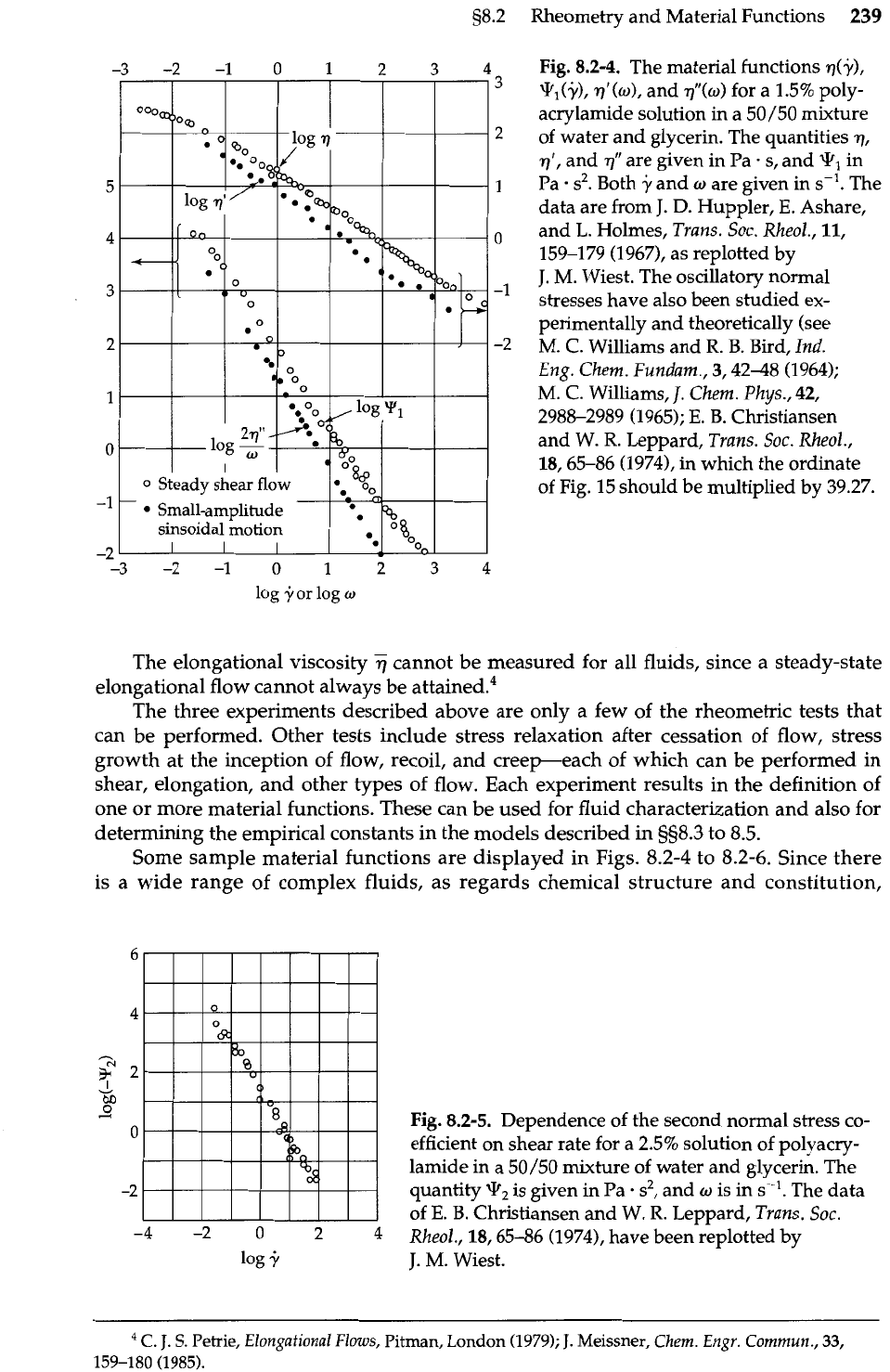
Rheometry and Material Functions
239
Fig.
8.2-4. The material functions q($,
ql(j),
qf(w), and
$(w)
for a 1.5% poly-
acrylamide solution in a 50/50 mixture
of water and glycerin. The quantities
7,
qt, and 7" are given in Pa
-
s, and
9,
in
Pa
s2. Both
j
and
o
are given in s-'. The
data are from
J.
D.
Huppler,
E.
Ashare,
and
L.
Holmes, Trans. Soc. Rheol.,
11,
159-179 (1967), as replotted by
J.
M.
Wiest. The oscillatory normal
stresses have also been studied ex-
perimentally and theoretically (see
M.
C. Williams and
R.
B.
Bird, Ind.
Eng. Chem. Fundam., 3/42-48 (1964);
M. C. Williams,
J.
Chern. Phys., 42,
2988-2989 (1965);
E.
B.
Christiansen
and W.
R.
Leppard, Trans. Soc. Xheol.,
18/65-86 (1974), in which the ordinate
of Fig. 15 should be multiplied by 39.27.
log
j
or log
w
The elongational viscosity
77
cannot be measured for all fluids, since a steady-state
elongational flow cannot always be attained.4
The three experiments described above are only a few of the rheometric tests that
can be performed. Other tests include stress relaxation after cessation of flow, stress
growth at the inception of flow, recoil, and creep-each of which can be performed in
shear, elongation, and other types of flow. Each experiment results in the definition of
one or more material functions. These can be used for fluid characterization and also for
determining the empirical constants in the models described
in
gs8.3 to 8.5.
Some sample material functions are displayed in Figs.
8.2-4
to 8.2-6. Since there
is a wide range of complex fluids, as regards chemical structure and constitution,
Fig.
8.2-5. Dependence of the second normal stress co-
efficient on shear rate for a 2.5% solution of polyacry-
lamide in a 50/50 mixture of water and glycerin. The
quantity
q2
is given in Pa. s2, and
o
is in s-l. The data
of
E.
B.
Christiansen and
W.
R.
Leppard, Trans. Soc.
Rheol., 18,6546 (1974), have been replotted by
J.
M.
Wiest.
C.
J.
S.
Petrie,
Elongational Flows,
Pitman,
London
(1979);
J.
Meissner,
Chem. Engr. Commun., 33,
159-180 (1985).

240
Chapter
8
Polymeric Liquids
log
i:
(a)
-3
-2 -1 0
log
(-a
(b)
Fig.
8.2-6. (a) Elongational viscosity for uniaxial stretching of low- and high-density polyeth-
ylene. [From
H.
Miinstedt and
H.
M.
Laun,
Rheol.
Acta, 20,211-221 (1981).1
(b)
Elongational
viscosity for biaxial stretching of low-density polyethylene, deduced from flow-birefringence
data. [From
J.
A.
van Aken and
H.
Janeschitz-Kriegl,
Rheol.
Acta, 20,419432 (1981).] In both
graphs the quantity
77
is given in Pa
.
s and
i.
is in s-l.
there are many types of mechanical responses in these various experiments. More
complete discussions of the data obtained in rheometric experiments are given else-
where."
58.3
NON-NEWTONIAN VISCOSITY AND
THE
GENERALIZED NEWTONIAN MODELS
This is the first of three sections devoted to empirical stress tensor expressions for non-
Newtonian fluids. One might say, very roughly, that these three sections satisfy three
different groups of people:
s8.3
The generalized Newtonian models are primarily used to describe steady-state
shear flows and have been widely used by engineers for designing flow systems.
58.4
The linear viscoelastic models are primarily used to describe unsteady-state flows
in systems with very small displacement gradients and have been used mainly
by chemists interested in understanding polymer structure.
58.5
The nonlinear viscoelastic models represent an attempt to describe all types of
flow (including the two listed above) and have been developed largely by
physicists and applied mathematicians interested in finding an all-inclusive theory.
Actually the three classes of models are interrelated, and each is important for understand-
ing the subject of non-Newtonian flow. In the following discussion of non-Newtonian
models, we assume throughout that the fluids are incompressible.
The generalized Newtonian models1 discussed here are the simplest of the three types
of
models to be discussed. However, they can describe only the non-Newtonian viscosity,
and none of the normal stress effects, time-dependent effects, or elastic effects. Nonethe-
R.
B.
Bird,
R.
C.
Armstrong, and
0.
Hassager,
Dynamics
of
Polymeric Liquids, Vol.
1,
Fluid
Mechanics,
Wiley-Interscience, 2nd edition
(1987).
'
K.
Hohenemser and
W.
Prager,
Zeits.
f.
Math. u.
Mech.,
12,216-226 (1932);
J.
G.
Oldroyd,
Proc.
Camb.
Phil.
Soc.,
45,595-611 (1949),
and
47,410-418 (1950).
James Gardner Oldroyd
(1921-1982),
a
professor at the University of Liverpool, made many contributions to the theory of non-Newtonian
fluids,
in
particular his ideas on the construction of constitutive equations and the principles of
continuum mechanics.

58.3
Non-Newtonian Viscosity and the Generalized Newtonian Models
241
less, in many processes in the polymer industry, such as pipe flow with heat transfer, dis-
tributor design, extrusion, and injection molding, the non-Newtonian viscosity and its
enormous variation with shear rate are central to describing the flows of interest.
For incompressible Newtonian fluids the expression for the stress tensor is given by
Eq.
1.2-7
with the last term omitted:
in which we have introduced the symbol
j
=
Vv
+
(VV)~, the rate-of-strain tensor (or rate-
of-deformation tensor). The generalized Newtonian fluid model is obtained by simply re-
placing the constant viscosity
p
by the non-Newtonian viscosity
v,
a function of the
shear rate, which in general can be written as the "magnitude of the rate-of-strain
tensor"
j
=
m;
it is understood that when the square root is taken, the sign must
be so chosen that
j
is a positive quantity. Then the generalized Newtonian fluid model is
The components of the rate-of-strain tensor
j
can be obtained in Cartesian, cylindrical,
and spherical coordinates from the right sides of the equations in Table
B.l
by omitting
the
(V
.
V)
terms as well as the factor (-p) in the remaining terms.
We now have to give an empiricism for the non-Newtonian viscosity function r](j).
Dozens of such expressions have been proposed, but we mention only two here:
(a)
The simplest empiricism for
~(j)
is the two-parameter power law expression:2
in which
m
and n are constants characterizing the fluid. This simple relation describes
the non-Newtonian viscosity curve over the linear portion of the log-log plot of the vis-
cosity versus shear rate for many materials (see, for example, the viscosity data in
Fig.
8.2-4). The parameter
m
has units of Pa sn, and
n
-
1 is the slope of the log
r]
vs. log
j
plot. Some sample values of power law parameters are given in Table 8.3-1.
Although the power law model was proposed as an empirical expression, it will be
seen in
Eq.
8.6-11 that
a
simple molecular theory leads to
a
power law expression for
high shear rates, with n
=
i.
Table
8.3-1
Power Law Parameters for Aqueous Solutionsa
Solution
-
-
Temperature
(K)
m(Pa. sn) n(-)
2.0%
hydroxyethylcellulose
293
313
333
0.5%
hydroxyethylcellulose
293
31
3
333
1.0%
polyethylene oxide
293
313
333
"
R.
M.
Turian,
Ph.D.
Thesis, University of Wisconsin, Madison
(1964),
pp.
142-148.
'
W. Ostwald,
Kolloid-Zeitschrift,
36,99-117 (1925);
A.
de
Waele,
Oil
Color Chem. Assoc.
J.,
6,33-88
(1923).

242
Chapter 8 Polymeric Liquids
Table
8.3-2
Parameters in the Carreau Model for Some
EXAMPLE
8.3-1
Laminar Flow of an
Incompressible Power
Law Fluid in a Circular
TU
be415
Solutions of Linear Polystyrene in 1-Chloronaphthalenea
Properties of
Parameters in Eq. 8.3-4
solution
(qm
is taken to be zero)
-
Mu
c
TO
A
n
(g/mol)
(g/ml)
(Pa. s) (s)
(-
-
-)
"
Values of the parameters are taken from
K.
Yasuda, R.
C.
Armstrong, and
R.
E.
Cohen,
Rheol. Acta,
20,163-178 (1981).
(b)
A
better curve fit for most data can be obtained by using the four-parameter
Car-
reau
equation:
which is
in which
r),
is the zero shear rate viscosity,
r],
is the infinite shear rate viscosity,
h
is a
pa-
rameter with units of time, and
n
is a dimensionless parameter. Some sample parameters
for the Carreau model are given in Table 8.3-2.
We
now give some examples of how to use the power law model. These are exten-
sions of problems discussed in Chapters
2
and
3
for Newtonian
fluid^.^
Derive the expression for the mass flow rate of a polymer liquid, described by the power
law
model. The fluid is flowing in a long circular tube of radius
R
and length
L,
as a result
of
a
pressure difference, gravity, or both.
SOLUTION
Equation 2.3-13 gives the shear stress distribution for any fluid
in
developed steady flow
in
a
circular tube. Into this expression we have to insert the shear stress for the power law fluid
(instead of using
Eq.
2.3-14). This expression may be obtained from Eqs. 8.3-2 and 3 above.
Since
v,
is ostulated to be a function of
v
alone, from Eq. B.l-13 we find that
j
=
=
dwe have to choose the sign for the square root so that
j
will be positive.
Since
dv,/dr
is negative in tube flow, we have to choose the minus sign, so that
P.
J.
Carreau, Ph.D. thesis, University of Wisconsin, Madison (1968). See also
K.
Yasuda,
R. C. Armstrong, and R.
E.
Cohen,
Rheol. Acta,
20,163-178 (1981).
For additional examples, including nonisothermal flows, see
R.
B.
Bird, R. C. Armstrong, and
0.
Hassager,
Dynamics of Polymeric Liquids, Vol.
1.
Fluid Mechanics,
Wiley-Interscience, New York, 2nd
edition (1998), Chapter
4.
M.
Reiner,
Deformation, Strain and Flow,
Interscience, New York, 2nd edition (19601,
pp.
243-245.

58.3 Non-Newtonian Viscosity and the Generalized Newtonian Models
243
Combining Eq. 8.3-6 and 2.3-13 then gives the following differential equation for the velocity:
After taking the nth root the equation may be integrated, and when the no-slip boundary con-
dition at
r
=
R
is used, we get
for the velocity distribution (see Eq. 8.1-1). When this is integrated over the cross section of
the circular tube we get
which simplifies to the Hagen-Poiseuille law for Newtonian fluids (Eq. 2.3-21) when
n
=
1
and
rn
=
p.
Equation 8.3-9 can be used along with data on pressure drop versus flow rate to
determine the power law parameters
rn
and
n.
The flow of a Newtonian fluid in a narrow slit is solved in Problem 2B.3. Find the velocity dis-
tribution and the mass flow rate for a power law fluid flowing in the slit.
Flow
of a Power Law
Fluid
in
a Narrow
Slit4
SOLUTION
The expression for the shear stress
T,
as
a
function of position
x
in
Eq. 2B.3-1 can be taken over
here, since it does not depend on the
type
of fluid. The power law formula for
7,
from Eq. 8.3-3 is
To get the velocity distribution for 0
5
x
5
B,
we substitute
rx,
from Eq. 8.3-10 into Eq. 2B.3-1
to get:
Integrating and using the no-slip boundary condition at
x
=
B
gives
Since we expect the velocity profile to be symmetric about the midplane
x
=
0, we can get the
mass rate of flow as follows:
When
n
=
1
and
rn
=
p,
the Newtonian result in Problem 2B.3 is recovered. Experimental
data on pressure drop and mass flow rate through a narrow slit can be used with Eq. 8.3-14 to
determine the power law parameters.
244
Chapter
8
Polymeric Liquids
Rework Example 3.6-3 for a power law fluid.
Tangential Annular
SOLUTION
'low
of
a
Power
Law
Equations 3.6-20 and 3.6-22 remain unchanged for a non-Newtonian fluid, but in lieu of
Eq
~luid~~~
3.6-21 we write the Bcomponent of the equation of motion in terms of the shear stress
by
using Table
B.5:
For the postulated velocity profile, we get for the power law model (with the help of Table
B.l)
Combining Eqs. 8.3-15 and 16 we get
Integration gives
Dividing by
r2
and taking the nth root gives a first-order differential equation for the angular
velocity
This may be integrated with the boundary conditions in Eqs. 3.6-27 and 28 to give
The (z-component of the) torque needed on the outer cylinder to maintain the motion is then
Combining Eqs. 8.3-20 and 21 then gives
The Newtonian result can be recovered by setting
n
=
1
and
rn
=
p.
Equation 8.3-22 can be
used
along with torque versus angular velocity data to determine the power law parameters
rn
and
n.
58.4
ELASTICITY
AND
THE
LINEAR
VISCOELASTIC
MODELS
Just after
Eq.
1.2-3,
in the discussion about generalizing Newton's "law of viscosity,"
we
specifically excluded time derivatives and time integrals in the construction of a linear
expression for the stress tensor in terms
of
the velocity gradients. In this section,
we

s8.4 Elasticity and the Linear Viscoelastic ModeIs
245
allow for the inclusion of time derivatives or time integrals, but still require a linear rela-
tion between
T
and
j.
This leads to
linear viscoelastic
models.
We start by writing Newton's expression for the stress tensor for an incompressible
viscous liquid along with Hooke's analogous expression for the stress tensor for an in-
compressible elastic solid:'
Newton:
Hooke:
In the second of these expressions
G
is the elastic modulus, and
u
is the "displacement
vector," which gives the distance and direction that a point in the solid has moved from
its initial position as a result of the applied stresses. The quantity
y
is called the "infini-
tesimal strain tensor." The rate-of-strain tensor and the infinitesimal strain tensor are re-
lated by
j
=
dy
/dt.
The Hookean solid has a perfect memory; when imposed stresses are
removed, the solid returns to its initial configuration. Hooke's law is valid only for very
small displacement gradients,
Vu.
Now we want to combine the ideas embodied in Eqs.
8.4-1 and
2
to describe viscoelastic fluids.
The
Maxwell
Model
The simplest equation for describing a fluid that is both viscous and elastic is the follow-
ing
Maxwell model:'
Here
A,
is a time constant (the
relaxation time)
and
17,
is the
zero shear rate viscosity.
When the stress tensor changes imperceptibly with time, then Eq. 8.4-3 has the form of
Eq. 8.4-1 for a Newtonian liquid. When there are very rapid changes in the stress ten-
sor with time, then the first term on the left side of Eq. 8.4-3 can be omitted, and when
the equation is integrated with respect to time, we get an equation of the form of Eq.
8.4-2 for the Hookean solid. In that sense, Eq. 8.4-3 incorporates both viscosity and
elasticity.
A
simple experiment that illustrates the behavior of a viscoelastic liquid involves
"silly putty." This material flows easily when squeezed slowly between the palms of the
hands, and this indicates that it is a viscous fluid. However, when it is rolled into a ball,
the ball will bounce when dropped onto a hard surface. During the impact the stresses
change rapidly, and the material behaves as an elastic solid.
The
Jeffreys
Model
The Maxwell model of Eq.
8.4-3
is a linear relation between the stresses and the velocity
gradients, involving a time derivative of the stresses. One could also include a time de-
rivative of the velocity gradients and still have a linear relation:
R.
Hooke,
Lectures de Potentia Restifutiva
(1678).
*
This relation was proposed by
J.
C.
Maxwell,
Phil.
Trans.
Roy. Soc.,
A157,49-88 (18671,
to
investigate the possibility that gases might be viscoelastic.

246
Chapter
8
Polymeric Liquids
This
Jeffreys modep
contains three constants: the zero shear rate viscosity and two time
constants (the constant
A,
is called the
retardation time).
One could clearly add terms containing second, third, and higher derivatives of
the
stress and rate-of-strain tensors with appropriate multiplicative constants, to get a
still
more general linear relation among the stress and rate-of-strain tensors. This gives
greater flexibility in fitting experimental data.
The Generalized Maxwell Model
Another way of generalizing Maxwell's original idea is to "superpose" equations of
the
form of Eq. 8.4-3 and write the
generalized Maxwell model
as
m
d
~(t)
=
~~(t) where
TL
+
A*
;ji
h
=
-7ky
(8.4-5/61
k=
1
in which there are many relaxation times
A,
(with
A,
r
A,
2
A,.
.
.)
and many constants
qk
with dimensions of viscosity. Much is known about the constants in this model from
polymer molecular theories and the extensive experiments that have been done on poly-
meric liq~ids.~
The total number of parameters can be reduced to three by using the following
em-
pirical
expression^:^
in which
7,
is the zero shear rate viscosity,
A
is
a time constant, and
a
is a dimensionless
constant (usually between
1.5
and 4).
Since Eq. 8.4-6 is a linear differential equation, it can be integrated analytically,
with
the condition that the fluid is at rest at
t
=
-
w.
Then when the various
lk
are summed
according to Eq. 8.4-5, we get the integral form of the generalized Maxwell model:
In this form, the "fading memory" idea is clearly present: the stress at time
t
depends
on
the velocity gradients at all past times t', but, because of the exponentials in the inte-
grand, greatest weight is given to times t' that are near
t;
that is, the fluid "memory"
is
better for recent times than for more remote times in the past. The quantity within braces
{
1
is called the
relaxation modulus
of the fluid and is denoted by
G(t
-
t').
The integral ex-
This model was suggested by
H.
Jeffreys,
The Earth,
Cambridge University Press, 1st edition
(1924), and 2nd edition (1929), p. 265, to describe the propagation of waves in the earth's mantle. The
parameters in this model have been related to the structure of suspensions and emulsions by
H.
Frohlich
and
R.
Sack,
Proc. Roy. Soc.,
A185,415430
(1946)
and by J.
G.
Oldroyd,
Proc. Roy. Soc.,
AZ18,122-132
(19531, respectively. Another interpretation of
Eq.
8.4-4 is to regard
it
as the sum of a Newtonian solvent
contribution
(s)
and a polymer contribution
(p),
the latter being described by a Maxwell model:
a
T,= -q,y;
T,+A,-T,= -7j
at
P
(8.4-4a,
b)
so that
T
=
T,
+
T~.
Then if Eqs. 8.4-4a, 8.4-4b, and
A,
times the time derivative of Eq. 8.4-4a are added,
we
get the Jeffreys model of
Eq.
8.44, with
7,
=
q,
+
qp
and
A,
=
(%/(q,
+
?,))A,.
*
J.
D.
Ferry,
Viscoelastic Properties of Polymers,
Wiley, New York, 3rd edition (1980). See also
N.
W. Tschoegl,
The Phenommological Theory of Linear Viscoelastic Behavior,
Springer-Verlag, Berlin (1989);
and
R.
B.
Bird,
R.
C.
Armstrong, and
0.
Hassager,
Dynamics of Polymeric Liquids, Vol.
I,
Fluid Mechanics,
Wiley-Interscience, New York, 2nd edition (1987), Chapter
5.
T.
W.
Spriggs,
Chem. Eng. Sci.,
20,931-940 (1965).
