Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

57.7 Use of the Macroscopic Balances for Unsteady-State Problems

217

An open cylinder of height

and radius R is initially entirely filled with a liquid. At time t

0 the liquid is allowed to drain out through a small hole of radius

at the bottom of the tank

Acceleration Effects in

(see

7.7-1

Unsteady

'low

from

(a)

Find the efflux time by using the unsteady-state mass balance and by assuming Torri-

Cylindrical Tank

celli's equation (see Problem 3B.14) to describe the relation between efflux velocity and the in-

stantaneous height of the liquid.

SOLUTION

(b)

Find the efflux time using the unsteady-state mass and mechanical energy balances.

(a)

We apply Eq. 7.1-2 to the system in Fig. 7.7-1, taking plane

to be at the top of the tank (so

that

0). If the instantaneous liquid height is h(t), then

Here we have assumed that the velocity profile at plane 2 is flat. According to Torricelli's

equation v2

so that Eq. 7.7-1 becomes

d t

(R)

When this is integrated from t

0 to

t,,,,, we get

in which

(R/Ro)4

This is effectively a quasi-steady-state solution, since we have

used the unsteady-state mass balance along with Torricelli's equation, which was derived for

a steady-state flow.

(b)

We now use Eq. 7.7-1 and the mechanical energy balance in Eq. 7.4-2. In the latter, the terms

and

are identically zero, and we assume that

is negligibly small, since the velocity gra-

dients in the system will be small. We take the datum plane for the potential energy to be at the

bottom

the tank, so that

gz,

0; at plane 1 no liquid is entering, and therefore the poten-

tial energy term is not needed there. Since the top of the tank is open to the atmosphere and the

tank is discharging into the atmosphere, the pressure contributions cancel one another.

To get the total kinetic energy in the system at any time t, we have to know the velocity

of every fluid element in the tank. At every point in the tank, we assume that the fluid is mov-

ing downward at the same velocity, namely V~(R~/R)~ so that the kinetic energy per unit vol-

ume is everywhere

$~;(R,/R)~.

To get the total potential energy in the system at any time t, we have to integrate the po-

tential energy per unit volume

pgz

over the volume of fluid from 0 to h. This gives ~R~p~($h~).

Therefore the mechanical energy balance in Eq. 7.4-2 becomes

From the unsteady-state mass balance,

-(R/RJ2(dh/dt). When this is inserted into

Eq.

7.7-4 we get (after dividing by dh/dt)

&let

radius

Fig.

7.7-1.

Flow out of a cylindrical tank.

218

Chapter 7 Macroscopic Balances for Isothermal Flow Systems

This is to be solved with the two initial conditions:

I.C.

0, h=H (7.7-6)

I.C. 2:

The second of these is Torricelli's equation at the initial instant of time.

The second-order differential equation for

can be converted to a first-order equation for

the function u(h) by making the change of variable (dh/dt)'

This gives

The solution to this first-order equation can be verified to be'

The second initial condition then gives

-4g/[N(N

2)HN-2] for the integration constant;

since N

we need not concern ourselves with the special case that N

We can next take

the square root of Eq. 7.7-9 and introduce

dimensionless liquid height

h/H;

this gives

which the minus sign must be chosen on physical grounds. This separable, first-order

equation can be integrated from

0 to

t,,,,

to give

The function

+(N)

gives the deviation from the quasi-steady-state solution obtained in

Eq.

7.7-3. This function can be evaluated as follows:

The integrations can now be performed. When the result is expanded in inverse powers of

one finds that

Since N

(R/RJ4

is a very large number, it is evident that the factor 4(N) differs only very

slightly from unity.

It is instructive now to return to Eq. 7.7-4 and omit the term describing the change

total kinetic energy with time. If this is done, one obtains exactly the expression for efflux

time in Eq. 7.7-3 (or Eq. 7.7-11, with +(N)

We can therefore conclude that in this type of

problem, the change in kinetic energy with time can safely be neglected.

See

Karnke,

Differentialgleichungen:

Losungsmethoden und Losungen,

Chelsea Publishing

Company,

New

York

(1948),

311, M.94;

M. Murphy,

Ordinay Differential Equations and Their

Solutions,

Van Nostrand, Princeton,

N.J.

(19601,

236,

#157.

57.7 Use of the Macroscopic Balances for Unsteady-State Problems

219

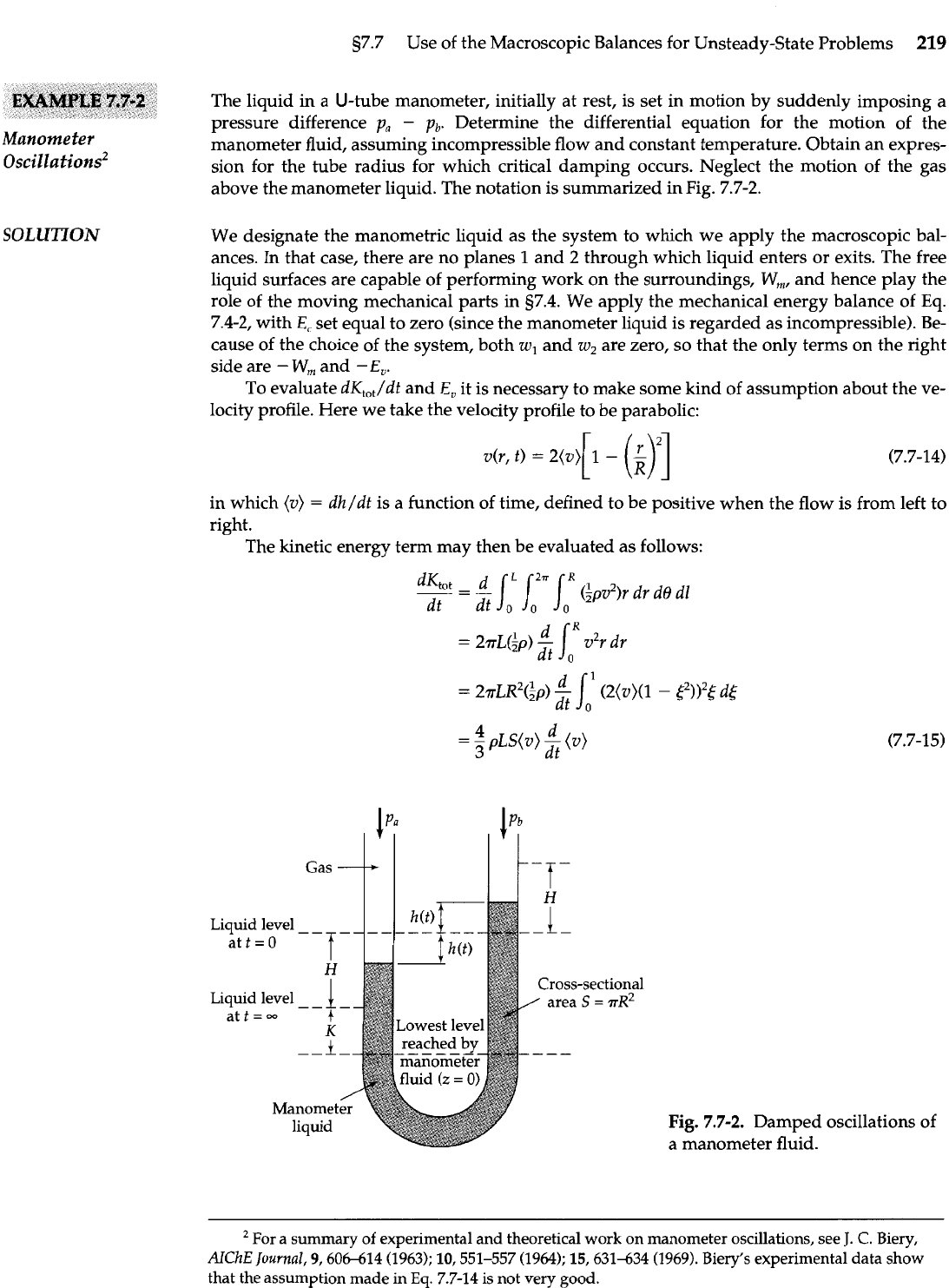
The liquid in a U-tube manometer, initially at rest, is set in motion by suddenly imposing a

pressure difference

pb.

Determine the differential equation for the motion of the

Manometer

manometer fluid, assuming incompressible flow and constant temperature. Obtain an expres-

Oscillations2

sion for the tube radius for which critical damping occurs. Neglect the motion of the gas

above the manometer liquid. The notation is summarized in Fig. 7.7-2.

SOLUTION

We designate the manometric liquid as the system to which we apply the macroscopic bal-

ances. In that case, there are no planes

and 2 through which liquid enters or exits. The free

liquid surfaces are capable of performing work on the surroundings, W,, and hence play the

role of the moving mechanical parts in 57.4. We apply the mechanical energy balance of Eq.

7.4-2, with

set equal to zero (since the manometer liquid is regarded as incompressible). Be-

cause of the choice of the system, both

and

are zero, so that the only terms on the right

side are

W, and

E,.

To evaluate

dKtOt/dt

and

it is necessary to make some kind of assumption about the ve-

locity profile. Here we take the velocity profile to be parabolic:

in which

(v)

dh/dt

is a function of time, defined to be positive when the flow is from left to

right.

The kinetic energy term may then be evaluated as follows:

Fig.

7.7-2.

Damped oscillations of

a manometer fluid.

For a summary of experimental and theoretical work on manometer oscillations, see

Biery,

AIChE

Journal,

9,606-614 (1963); 10,551-557 (1964); 15,631-634 (1969).

Biery's experimental data show

that the assumption made in

Eq.

7.7-14

is not very good.

220

Chapter 7 Macroscopic Balances for Isothermal Flow Systems

Here

is a coordinate running along the axis of the manometer tube, and

is the distance

along this axis from one manometer interface to the other-that is, the total length of the

manometer fluid. The dimensionless coordinate

r/R,

and

is the cross-sectional area

the tube.

The change of potential energy with time is given by

[(intFEril

over portion

K+H-h

K+H+)I

below

0, which

)

pgS

pgs

dz]

is constant

The viscous loss term can also be evaluated as follows:

Furthermore, the net work done by the surroundings on the system is

Substitution of the above terms into the mechanical energy balance and letting

(v)

dh/dt

then gives the differential equation for

k(t)

which is to be solved with the initial conditions that

and

dh/dt

0. This second-

order, linear, nonhomogeneous equation can be rendered

new variable

defined by

Then the equation for the motion of the manometer liquid is

homogeneous by introducing

(7.7-20)

This equation also arises in describing the motion of a mass connected to a spring and

dash-

pot as well as the current

RLC

circuit (see Eq. C.l-7).

We now try a solution of the form

em'.

Substituting this trial function into Eq.

7.7-21

shows that there are two admissible values for

and the solution is

C+em-'

C-em-t

when

(7.7-23)

Clemt

C2temf

when

(7.7-24)

with the constants being determined by the initial conditions.

57.8

Derivation of the Macroscopic Mechanical Energy Balance

221

The type of motion that the manometer liquid exhibits depends on the value of the dis-

criminant

Eq.

7.7-22:

(a) If (6p,/pR2I2

(6g/L),

the system is overdamped, and the liquid moves slowly to its final

position.

(b) If (6p,/p~~)~

(6g/L),

the system is underdamped, and the liquid oscillates about its

final position, the oscillations becoming smaller and smaller.

(c)

(6g/L),

the system is critically damped, and the liquid moves to its final

position in the most rapid monotone fashion.

The tube radius for critical damping is then

If the tube radius

is greater than

R,,,

an oscillatory motion occurs.

57.8

DERIVATION OF THE MACROSCOPIC

MECHANICAL ENERGY BALANCE'

Eq.

7.4-2 the macroscopic mechanical energy balance was presented without proof. In

this section we show how the equation is obtained by integrating the equation of change

for mechanical energy (Eq. 3.3-2) over the entire volume of the flow system of Fig. 7.0-1.

We begin by doing the formal integration:

(iPg

p6) d~

(iP9

p6)v) d~

pv) d~

vl) d~

V(t)

p(V v) dV

(.r:Vv) dV

(7.8-1)

V(t) V(t)

Next we apply the 3-dimensional Leibniz formula (Eq. A.5-5) to the left side and the

Gauss divergence theorem (Eq. A.5-2) to terms 1,2, and

on the right side.

vl)

p(v

v) d~

(.r:vv) d~

(7.8-2)

S(t) V(t) V(t)

The term containing v,, the velocity of the surface of the system, arises from the applica-

tion of the Leibniz formula. The surface

S(t)

consists of four parts:

the fixed surface

(on which both v and v, are zero)

the moving surfaces

(on which v

v, with both nonzero)

the cross section of the entry port

(where v,

the cross section of the exit port S2 (where

Presently each of the surface integrals will be split into four parts corresponding to these

four surfaces.

We now interpret the terms in Eq. 7.8-2 and, in the process, introduce several as-

sumptions; these assumptions have already been mentioned in

$57.1

7.4,

but now the

reasons for them will be made clear.

Bird,

Korean

Chem. Eng.,

15,105-123

(1998),

93.

222

Chapter 7 Macroscopic Balances for Isothermal Flow Systems

The term on the left side can be interpreted as the time rate of change of the total

ki-

netic and potential energy

(K,,

a,,,)

within the "control volume," whose shape and

volume are changing with time.

We next examine one by one the five terms on the right side:

Term

(including the minus sign) contributes only at the entry and exit ports and

gives the rates of influx and efflux of kinetic and potential energy:

The angular brackets indicate an average over the cross section. To get this result we

have to assume that the fluid density and potential energy per unit mass are constant

over the cross section, and that the fluid is flowing parallel to the tube walls at the entry

and exit ports. The first term in Eq. 7.8-3 is positive, since at plane

(-n

(ul

(ulv,))

v,,

and the second term is negative, since at plane

(-n

(-u, .

(u2v2))

-v2.

Term

(including the minus sign) gives no contribution on Sf since v is zero there.

On each surface element dS of S, there is a force -npdS acting on a surface moving with

a velocity v, and the dot product of these quantities gives the rate at which the surround-

ings do work on the fluid through the moving surface element dS. We use the symbol

w:'

to indicate the sum of all these surface terms. Furthermore, the integrals over the

stationary surfaces S, and S, give the work required to push the fluid into the system

plane

minus the work required to push the fluid out of the system at plane

Therefore

term

finally gives

Term

pl(vl)S,

p,(v2)S2

w?)

(7.8-4)

Here we have assumed that the pressure does not vary over the cross section at the entry

and exit ports.

Term

(including the minus sign) gives no contribution on Sf since v is zero there.

The integral over S,, can be interpreted as the rate at which the surroundings do work

the fluid by means of the viscous forces, and this integral is designated as

w:'.

At the

entry and exit ports it is conventional to neglect the work terms associated with the

vis-

cous forces, since they are generally quite small compared with the pressure contribu-

tions. Therefore we get

Term 3

WI;'

(7.8-5)

We now introduce the symbol

w!:)

w:'

to represent the total rate at which

the surroundings do work on the fluid within the system through the agency of the mov-

ing surfaces.

Terms

and

cannot be further simplified, and hence we define

Term

p(V

v) dV

-E,

V(f)

Term

(.r:Vv) dV

(7.8-7)

V(D

For Newtonian fluids the viscous loss

EL,

is the rate at which mechanical energy is

irre-

versibly

degraded into thermal energy because of the yiscosity of the fluid and is always

a positive quantity (see Eq. 3.3-3). We have already discussed methods for estimating

57.5.

(For viscoelastic fluids, which we discuss in Chapter 8,

has to be interpreted

differently and may even be negative.) The compression term

is the rate at which

me-

chanical energy is

reversibly

changed into thermal energy because of the compressiblity

of the fluid; it may be either positive or negative. If the fluid is being regarded as incom-

pressible, then

is zero.

s7.8 Derivation of the Macroscopic Mechanical Energy Balance

223

When all the contributions are inserted into Eq. 7.8-2 we finally obtain the macro-

scopic mechanical energy balance:

If, now, we introduce the symbols

pl(vl)Sl and w2

p2(u2)S2 for the mass rates of

flow in and out, then Eq. 7.8-8 can be rewritten in the form of Eq. 7.4-2. Several assump-

tions have been made in this development, but normally they are not serious. If the situ-

ation warrants, one can go back and include the neglected effects.

It should be noted that the above derivation of the mechanical energy balance does

not require that the system be isothermal. Therefore the results in Eqs. 7.4-2 and 7.8-8 are

valid for nonisothermal systems.

To get the mechanical energy balance in the form of Eq.

7.4-7

we have to develop an

approximate

expression for

E,.

We imagine that there is a representative streamline run-

ning through the system, and we introduce a coordinate

along the streamline. We as-

sume that pressure, density, and velocity do not vary over the cross section.

further

imagine that at each position along the streamline, there is a cross section S(s) perpendic-

ular to the s-coordinate, so that we can write dV

S(s)ds. If there are moving parts in the

system and if the system geometry is complex, it may not be possible to do this.

We start by using the fact that (V

pv)

at steady state so that

Then we use the assumption that the pressure and density are constant over the cross

section to write approximately

Even though p,

and

are functions of the streamline coordinate

their product, w

pvS,

is a constant for steady-state operation and hence may be taken outside the integral. This

gives

Then an integration by parts can be performed:

When this result is put into Eq. 7.4-5, the approximate relation in Eq. 7.4-7

obtained. Be-

cause of the questionable nature of the assumptions made (the existence of a representative

streamline and the constancy of

and

over a cross section), it seems preferable to use Eq.

7.4-5 rather than Eq. 7.47. Also, Eq. 7.45 is easily generalized to systems with multiple inlet

and outlet ports, whereas Eq. 7.47 is not; the generalization

given in

Eq.

(D)

of Table 7.6-1.

QUESTIONS

FOR

DISCUSSION

Discuss the origin, meaning, and use of the macroscopic balances, and explain what assump-

tions have been made in deriving them.

How does one decide which macroscopic balances to use for

given problem? What auxiliary

information might one need in order to solve problems with the macroscopic balances?

Are friction factors and friction loss factors related? If so, how?

224

Chapter 7 Macroscopic Balances for Isothermal Flow Systems

Discuss the viscous loss

and the compression term

E,,

with regard to physical interpreta-

tion, sign, and methods of estimation.

How is the macroscopic mechanical energy balance related to the Bernoulli equation for in-

viscid fluids? How is it derived?

What happens in Example 7.3-1 if one makes a different choice for the origin of the coordinate

system?

In Example 7.5-1 what would be the error in the final result if the estimation of the viscous

loss

were off by a factor of 2? Under what circumstances would such an error be more seri-

ous?

In Example 7.5-1 what would happen if

ft were replaced by 50 ft?

In Example 7.6-3, how would the results be affected if the outlet pressure were 11 atm instead

of 1.1 atm?

10.

List all the assumptions that are inherent in the equations given in Table 7.6-1.

PROBLEMS

7A.1

Pressure rise in a sudden enlargement (Fig. 7.6-1). An aqueous salt solution is flowing

through a sudden enlargement at a rate of 450 US. gal/min

0.0384 m3/s. The inside

diameter of the smaller pipe is

in. and that of the large pipe is

in. What is the pressure rise

in pounds per square inch if the density of the solution is 63 lb,/ft3? Is the flow in the smaller

pipe laminar or turbulent?

Answer:

0.157 psi

1.08

lo3

N/m2

7A.2

Pumping

hydrochloric acid solution (Fig. 7A.2). A dilute HC1 solution of constant density

and viscosity

62.4 lb,/ft3,

cp) is to be pumped from tank

to tank 2 with no overall

change in elevation. The pressures in the gas spaces of the two tanks are

atm and

atm. The pipe radius is 2 in. and the Reynolds number is 7.11

lo4.

The average velocity

the pipe is to be 2.30 ft/s. What power must be delivered by the pump?

Answer:

2.4 hp

1.8

Fig.

7A.2.

Pumping of a hydrochloric acid

- -

inside

radius

solution.

7A.3

Compressible gas flow in

cylindrical pipe. Gaseous nitrogen is in isothermal turbulent

flow at 25°C through a straight length of horizontal pipe with 3-in. inside diameter at a rate

0.28 1bJs. The absolute pressures at the inlet and outlet are 2 atm and

atm, respectively.

Evaluate

k,,

assuming ideal gas behavior and radially uniform velocity distribution.

Answer:

26.3 Btu/lb,

6.12

lo4

J/kg

7A.4

Incompressible

flow

in an annulus. Water at 60°F is being delivered from a pump through

coaxial annular conduit 20.3

long at a rate of 241

U.S.

gal/min. The inner and outer radii of

the annular space are 3 in. and 7 in. The inlet is

ft lower than the outlet. Determine the

power output required from the pump. Use the mean hydraulic radius empiricism to solve

the problem. Assume that the pressures at the pump inlet and the annular outlet are the

same.

Answer:

0.31 hp

0.23 kW

Problems

225

7A.5

Force on a U-bend

(Fig. 7A.5). Water at 68°F

62.4 lb,/ft3,

cp) is flowing in turbu-

lent flow in a U-shaped pipe bend at 3 ft3/s. What is the horizontal force exerted by the water

on the U-bend?

Answer:

903 lbf

'lane

19 psia

-1

internal

diameter

Fig.

7A.5.

Flow in a U-bend; both arms of the bend are at

psis

the same elevation.

7A.6

Flow-rate calculation

(Fig. 7A.6). For the system shown in the figure, calculate the volume

flow rate of water at 68OF.

Fig.

7A.6.

Flow from a constant-head tank.

7A.7

Evaluation of various velocity averages from Pitot tube data.

Following are some experi-

mental data1 for a Pitot tube traverse for the flow of water in a pipe of internal radius 3.06 in.:

Plot these data and find out whether the flow is laminar or turbulent. Then use Simpson's

rule for numerical integration to compute (v)/v,,,, (v2)/v~,,, and (v3)/vi,,. Are these results

consistent with the values of 50/49 (given just before Example 7.2-1) and 43200/40817 (given

just before Example 7.4-I)?

Distance from Local velocity

Position tube center (in.) (ft/s)

B. Bird,

thesis, University of Wisconsin (1915).

Distance from Local velocity

Position tube center (in.) (ft/s)

226

Chapter 7 Macroscopic Balances for Isothermal Flow Systems

Velocity averages from the

power law. Evaluate the velocity ratios in Problem 7A.7 ac-

cording to the velocity distribution in Eq. 5.1-4.

Relation between force and viscous loss fpr flow in conduits of variable cross section.

Equation 7.5-6 gives the relation

Ff,,

pSE, between the drag force and viscous loss for

straight conduits of arbitrary, but constant, cross section. Here we consider a straight horizon-

tal channel whose cross section varies gradually with the downstream distance. We restrict

ourselves to axisymmetrical channels, so that the drag force is axially directed.

If the cross section and pressure at the entrance are

and pl, and those at the exit are

and p,, then prove that the relation analogous to Eq. 7.5-7 is

where

Interpret the results.

Flow through a sudden enlargement (Fig.

7.6-1).

A fluid is flowing through a sudden en-

largement, in which the initial and final diameters are

and D2 respectively. At what ratio

D,/D, will the pressure rise p2

p1 be a maximum for a given value of

v,?

Answer:

D2/Dl

Flow between two tanks (Fig. 7B.4).

Case

fluid flows between two tanks A and

because

pPB. The tanks are at the same elevation and there is no pump in the line. The connecting

line has a cross-sectional area S, and the mass rate of flow is

for a pressure drop of (p,

p,),.

Case

1%.

It is desired to replace the connecting line by two lines, each with cross section

SII

is1. What pressure difference (pA

pJI, is needed to give the same total mass flow rate as in

Case

Assume turbulent flow and use the Blasius formula (Eq. 6.2-12) for the friction factor.

Neglect entrance and exit losses.

Answer:

(p,

p&,/(pA

pdl

z5"

Circular tube of

cross section

Mass

flow

rate

Fig.

7B.4.

Flow between two tanks.

Circular tubes

cross

section

SII

Revised design of an air duct (Fig.

7B.5).

A straight, horizontal air duct was to be installed in

a factory.

The

duct was supposed to be

ft in cross section. Because of an obstruction,

the duct may be only

ft high, but it may have any width. How wide should the duct be

have the same terminal pressures and same volume rate of flow? Assume that the flow is

tur-

bulent and that the Blasius formula

(Eq.

6.2-12) is satisfactory for this calculation. Air can

regarded as incompressible in this situation.

(a) Write the simplified versions of the mechanical energy balance for ducts I and 11.

(b)

Equate the pressure drops for the two ducts and obtain an equation relating the widths

and heights of the two ducts.

(c)

Solve the equation in

(b)

numerically to find the width that should be used for duct 11.

Answer:

(c)

9.2

/-x

Sum

of mass

flow rates is