Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.

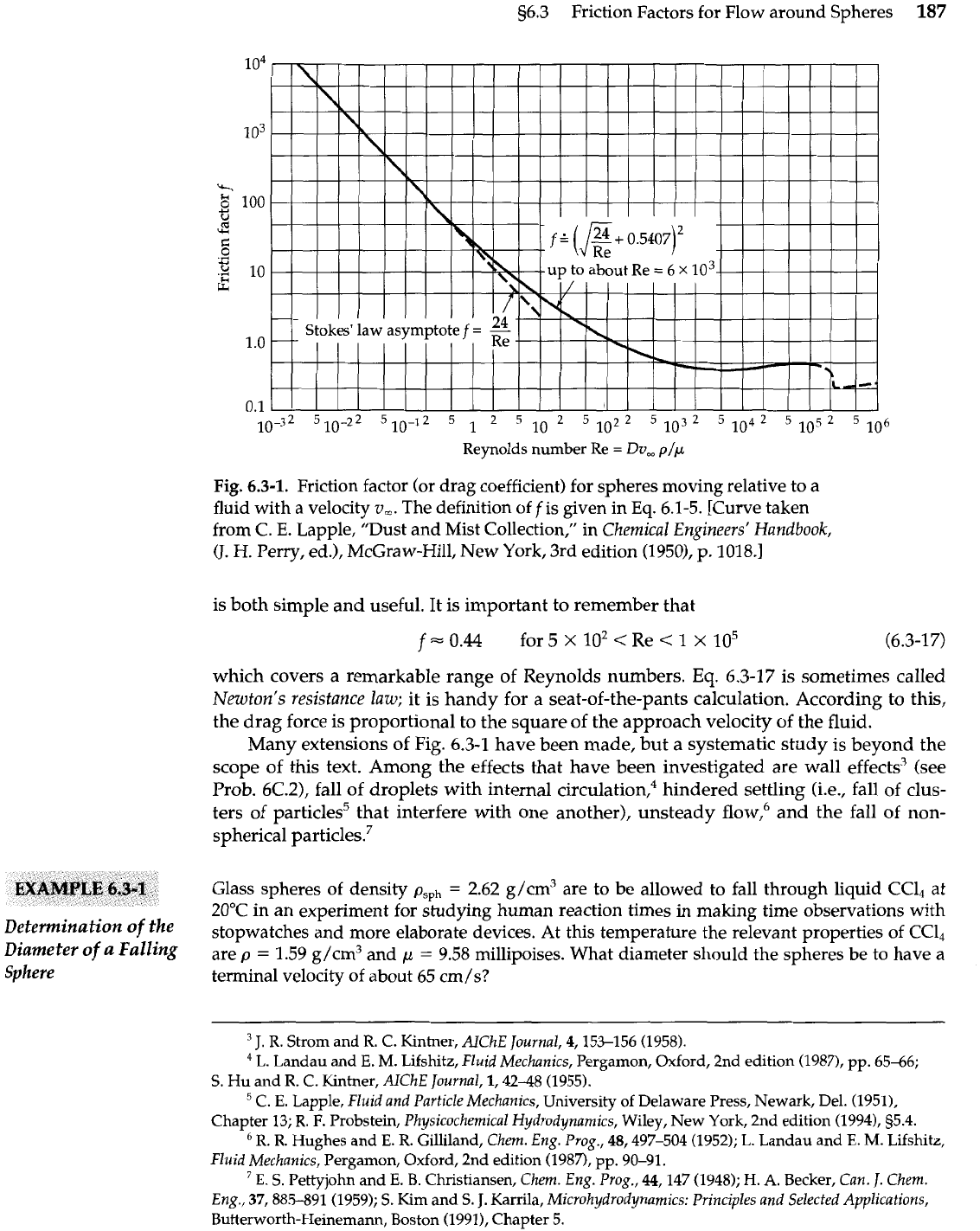
56.3 Friction Factors for Flow around Spheres
187
Reynolds number Re
=
Dv,
p/p
Fig.
6.3-1.
Friction factor (or drag coefficient) for spheres moving relative to a
fluid with a velocity
v,.
The definition off is given in
Eq.
6.1-5.
[Curve taken
from C.
E.
Lapple, "Dust and Mist Collection," in Chemical Engineers' Handbook,
(J.
H.
Perry,
ed.),
McGraw-Hill, New York, 3rd edition (1950), p.
1018.1
is both simple and useful. It is important to remember that
f
=
0.44
for
5
x
lo2
<
Re
<
1
X
lo5
(6.3-17)
which covers a remarkable range of Reynolds numbers.
Eq.
6.3-17
is sometimes called
Newton's resistance
law;
it is handy for a seat-of-the-pants calculation. According to this,
the drag force is proportional to the square of the approach velocity of the fluid.
Many extensions of Fig. 6.3-1 have been made, but a systematic study is beyond the
scope of this text. Among the effects that have been investigated are wall effectsvsee
Prob.
6C.2),
fall
of
droplets with internal circulation,4 hindered settling (i.e., fall of clus-
ters of particles5 that interfere with one another), unsteady flow: and the fall of non-
spherical particles7
Glass spheres of density
p,,,
=
2.62 g/cm" are to be allowed to fall through liquid CC14 at
20°C in
an
experiment for studying human reaction times in making time observations with
Detemination
of
the
stopwatches and more elaborate devices. At this temperature the relevant properties of CCl,
Diameter of a Falling
are
p
=
1.59 g/cm3 and
p
=
9.58 millipoises. What diameter should the spheres be to have a
Sphere
terminal velocity of about
65
cm/s?
J.
R.
Strom and
R.
C.
Kintner,
AIChE Journal,
4,153-156 (1958).
L.
Landau and
E.
M.
Lifshitz,
Fluid Mechanics,
Pergamon, Oxford, 2nd edition (1987), pp. 65-66;
S.
Hu and R.
C.
Kintner,
AIChE Journal,
1,42-48 (1955).
C.
E.
Lapple,
Fluid and Particle Mechanics,
University of Delaware Press, Newark, Del. (19511,
Chapter 13; R.
F.
Probstein,
Physicochemical Hydrodynamics,
Wiley, New York, 2nd edition (1994),
g5.4.
R. R. Hughes and
E.
R. Gilliland,
Chem. Eng. Prog.,
48,497-504 (1952); L. Landau and
E.
M.
Lifshitz,
Fluid Mechanics,
Pergamon, Oxford, 2nd edition (19871, pp. 90-91.
E.
S.
Pettyjohn and
E.
B. Christiansen,
Chem. Eng. Prog.,
44,147 (1948);
H.
A.
Becker,
Can.
J.
Chem.
Eng.,
37,885-891 (1959);
S.
Kim and
S.
J.
Karrila,
Microhydrodynamics: Principles and Selected Applications,
Butterworth-Heinemann, Boston (19911, Chapter 5.
188
Chapter 6 Interphase Transport in Isothermal Systems
SOLUTION
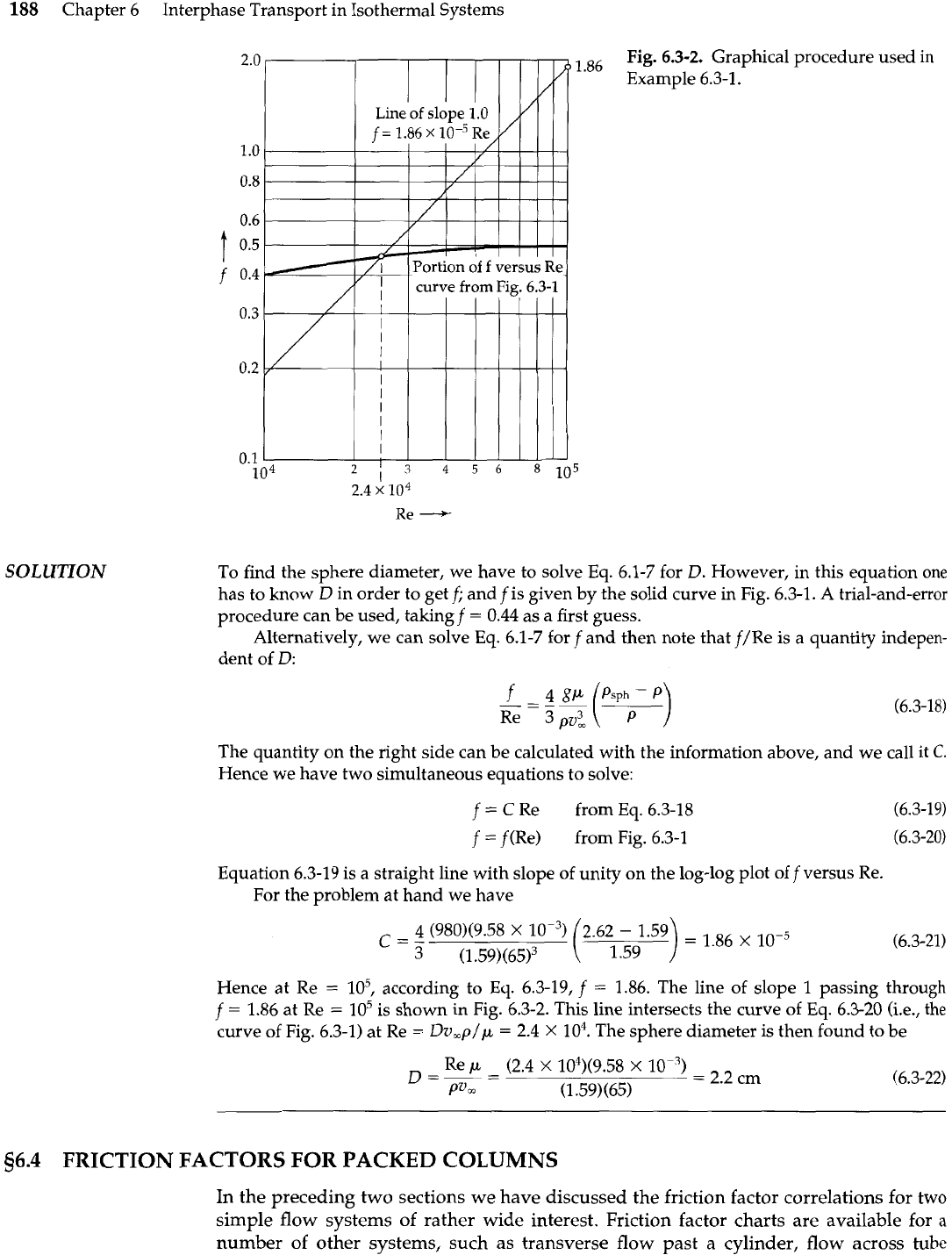
Fig.
6.3-2.
Graphical procedure used
in
Example 6.3-1.
To find the sphere diameter, we have to solve Eq. 6.1-7 for
D.
However, in this equation one
has to know
D
in order to get
f;
and
f
is given by the solid curve in Fig. 6.3-1.
A
trial-and-error
procedure can be used, taking
f
=
0.44 as a first guess.
Alternatively, we can solve Eq. 6.1-7 for
f
and then note that f/Re is a quantity indepen-
dent of
D:
The quantity on the right side can be calculated with the information above, and we call
it
C.
Hence we have two simultaneous equations to solve:
f
=
C
Re from Eq. 6.3-18
f
=
f
(Re)
from Fig. 6.3-1
Equation 6.3-19 is a straight line with slope of unity on the log-log plot off versus Re.
For the problem at hand we have
Hence at Re
=
lo5,
according to Eq. 6.3-19,
f
=
1.86. The line of slope
1
passing through
f
=
1.86 at Re
=
lo5
is shown in Fig. 6.3-2. This line intersects the curve of Eq. 6.3-20 (i.e., the
curve of Fig. 6.3-1) at Re
=
Da,p/p
=
2.4
X
lo4.
The sphere diameter is then found to be
g6.4
FRICTION FACTORS FOR PACKED COLUMNS
In the preceding two sections we have discussed the friction factor correlations for two
simple flow systems of rather wide interest. Friction factor charts are available for
a
number of other systems, such as transverse flow past a cylinder, flow across tube

56.4
Friction Factors for Packed Columns
189
banks, flow near baffles, and flow near rotating disks. These and many more are sum-
marized in various reference works.' One complex system of considerable interest in
chemical engineering is the packed column, widely used for catalytic reactors and for
separation processes.
There have been two main approaches for developing friction factor expressions for
packed columns. In one method the packed column is visualized as a bundle of tangled
tubes of weird cross section; the theory is then developed by applying the previous re-
sults for single straight tubes to the collection of crooked tubes. In the second method the
packed column is regarded as a collection of submerged objects, and the pressure drop is
obtained by summing up the resistances of the submerged
particle^.^
The tube bundle
theories have been somewhat more successful, and we discuss them here. Figure 6.4-l(a)
depicts a packed column, and Fig. 6.4-l(b) illustrates the tube bundle model.
A
variety of materials may be used for the packing in columns: spheres, cylinders,
Berl saddles, and so on. It is assumed throughout the following discussion that the pack-
ing is statistically uniform, so that there is no "channeling" (in actual practice, channeling
frequently occurs, and then the development given here does not apply). It is further as-
sumed that the diameter of the packing particles is small in comparison to the diameter of
the column in which the packing is contained, and that the column diameter is uniform.
We define the friction factor for the packed column analogously to Eq.
6.1-4:
in which
L
is the length of the packed column,
D,
is the effective particle diameter (de-
fined presently), and
v,
is the
superficial
velocity;
this is the volume flow rate divided by
the empty column cross section,
v,
=
w/pS.
The pressure drop through a representative tube in the tube bundle model is given
by
Eq.
6.2-17
Fig.
6.4-1.
(a)
A
cylindrical tube packed with spheres;
(b)
(b)
a
"tube bundle" model for the packed column in
(a).
--
-
P.
C.
Carman,
Flow of Gases through Porous Media,
Butterworths, London (1956);
J.
G.
Richardson,
section 16 in
Handbook of Fluid Dynamics
(V.
L.
Streeter,
ed.),
McGraw-Hill, New York (1961);
M.
Kaviany,
Chapter 21 in
The Handbook of Fluid Dynamics
(R.
W.
Johnson, ed.), CRC Press, Boca Raton, Fla. (1998).
W.
E.
Ranz,
Chem. Eng. Prog.,
48,274-253 (1952);
H.
C. Brinkman,
Appl. Sci. Research.,
Al,
27-34,
81-86,333-346 (1949).
Henri Coenraad Brinkman
(1908-1961) did research on viscous dissipation
heating, flow in porous media, and plasma physics; he taught at the University of Bandung, Indonesia,
from 1949 to 1954, where he wrote
The Application of Spinor Invariants to Atomic Physics.

190
Chapter
6
Interphase Transport in Isothermal Systems
in which the friction factor for a single tube,
f,,,,
is a function of the Reynolds number
Reh
=
4Rh(v)p/p. When this pressure difference is substituted into Eq. 6.4-1, we get
In the second expression, we have introduced the void fraction,
E,
the fraction of space
in
the column not occupied by the packing. Then
vo
=
(v)~,
which results from the defini-
tion of the superficial velocity. We now need an expression for Rh.
The hydraulic radius can be expressed in terms of the void fraction
E
and the wetted
surface a per unit volume of bed as follows:
Rh=(
cross section available for flow
wetted perimeter
=
(volume available for flow
total wetted surface
volume of voids
-
volume of bed
-
-
-
wetted surface
volume of bed
The quantity a is related to the "specific surface"
a,
(total particle surface per volume
of
particles) by
The quantity a, is in turn used to define the mean particle diameter
Dp
as follows:
This definition is chosen because, for spheres of uniform diameter, Dp is exactly the
di-
ameter of a sphere. From the last three expressions we find that the hydraulic radius
is
Rh
=
DP&/6(1
-
e).
When this is substituted into
Eq.
6.4-3, we get
We now adapt this result to laminar and turbulent flows by inserting appropriate
ex-
pressions for
ftube.
(a)
For laminar
flow
in tubes,
fbbe
=
16/Reh. This is exact for circular tubes only.
To
account for the noncylindrical surfaces and tortuous fluid paths encountered in
typical
packed-column operations, it has been found that replacing 16 by 100/3 allows the
tube
bundle model to describe the packed-column data. When this modified expression
for
the tube friction factor is used, Eq. 6.4-7 becomes
in which
Go
=
pv,
is the mass flux through the system. When this expression for
f
is
sub-
stituted into Eq. 6.4-1 we get

56.4 Friction Factors for Packed Columns
191
which is the Blake-Kozeny equatiom3 Equations 6.4-8 and
9
are generally good for
(DpG,/p(l
-
E))
<
10 and for void fractions less than
E
=
0.5.
(b)
For highly turbulent flow a treatment similar to the above can be given. We begin
again with the expression for the friction factor definition for flow in a circular tube. This
time, however, we note that, for highly turbulent flow in tubes with any appreciable
roughness, the friction factor is a function of the roughness only, and is independent of
the Reynolds number. If we assume that the tubes in all packed columns have similar
roughness characteristics, then the value off,,, may be taken to be the same constant for
all systems. Taking
ftube
=
7/12 proves to be an acceptable choice. When this is inserted
into Eq. 6.4-7, we get
When this is substituted into Eq. 6.4-1, we get
which is the Burke-Plummer4 equation, valid for (DpGo/p(l
-
8))
>
1000. Note that the
dependence on the void fraction is different from that for laminar flow.
(c)
For the transition region, we may superpose the pressure drop expressions for (a)
and
(b)
above to get
For very small vo, this simplifies to the Blake-Kozeny equation, and for very large vo, to
the Burke-Plummer equation. Such empirical superpositions of asymptotes often lead to
satisfactory results. Equation 6.4-12 may be rearranged to form dimensionless groups:
This is the Ergun equation: which is shown in Fig. 6.4-2 along with the Blake-Kozeny and
Burke-Plummer equations and experimental data. It has been applied with success to
gas flow through packed columns by using the density
p
of the gas at the arithmetic av-
erage of the end pressures. Note that Go is constant through the column, whereas vo
changes through the column for a compressible fluid. For large pressure drops, however,
it seems more appropriate to apply Eq. 6.4-12 locally by expressing the pressure gradient
in differential form.
The Ergun equation is but one of many6 that have been proposed for describing
packed columns. For example, the Tallmadge equation7
is reported to give good agreement with experimental
(D,G,/~(I
-
EN
<
lo5.
data over the range
0.1
<
9.
C.
Blake,
Trans. Amer. Inst. Chem. Engrs.,
14,415421 (1922);
J.
Kozeny,
Sitzungsber. Akad. Wiss. Wien,
Abt.
11~1,136,271-306 (1927).
S.
P.
Burke and
W.
B.
Plummer,
Ind. Eng. Chem.,
20,1196-1200 (1928).
S. Ergun,
Chem. Engr. Prog.,
48,89-94 (1952).
I.
F.
Macdonald, M. S. El-Sayed,
K.
Mow, and
F.
A.
Dullien,
Ind. Eng. Chem. Fundam.,
18,199-208
(1979).
'
J.
A.
Tallmadge,
AIChE journal,
16,1092-1093 (1970).
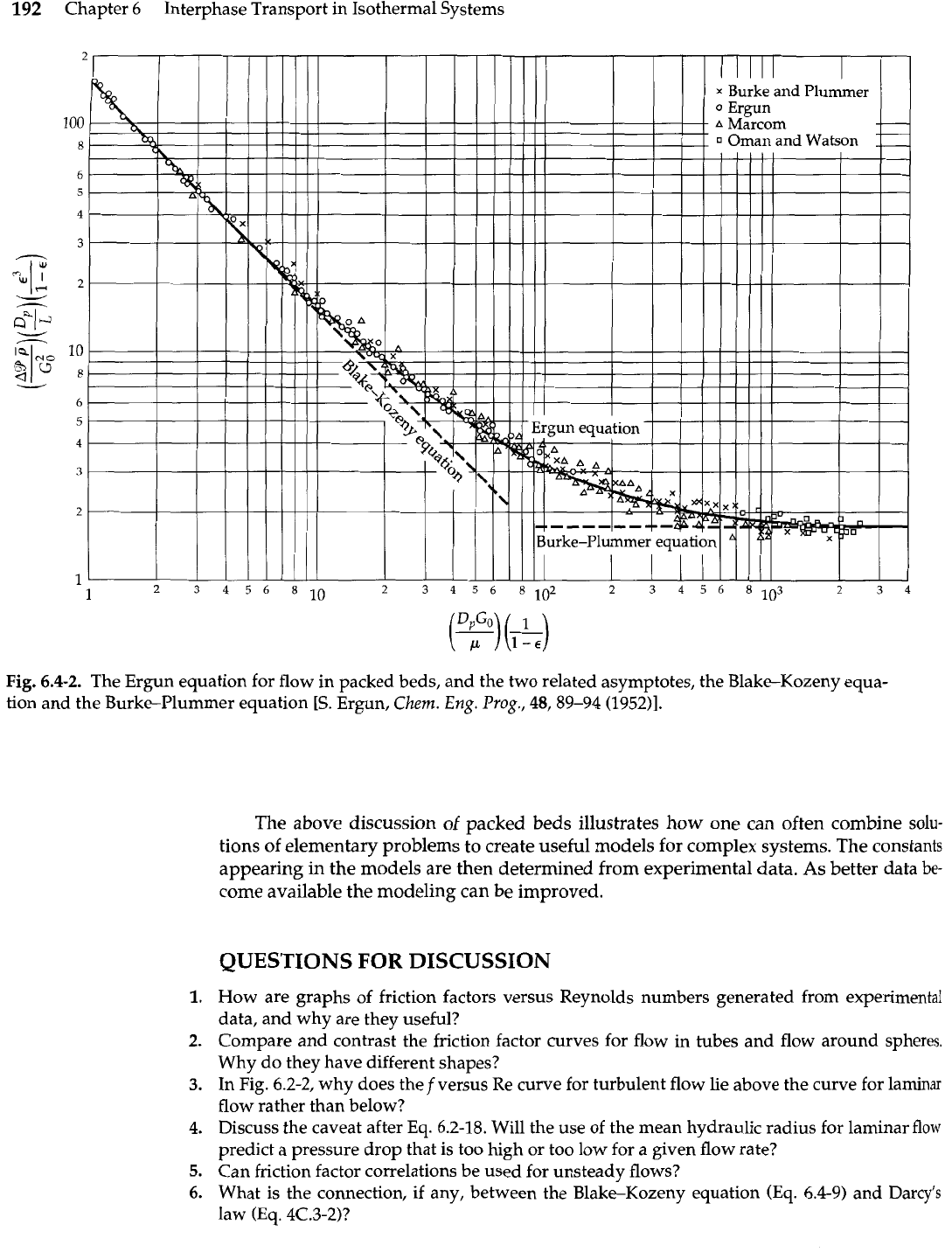
192
Chapter
6
Interphase Transport in Isothermal Systems
Fig.
6.4-2.
The Ergun equation for flow in packed beds, and the two related asymptotes, the Blake-Kozeny equa-
tion and the Burke-Plummer equation [S. Ergun,
Chem.
Eng. Prog., 48,89-94 (195211.
The above discussion of packed beds illustrates how one can often combine solu-
tions of elementary problems to create useful models for complex systems. The constants
appearing in the models are then determined from experimental data. As better data
be-
come available the modeling can be improved.
QUESTIONS FOR DISCUSSION
1.
How are graphs of friction factors versus Reynolds numbers generated from experimental
data, and why are they useful?
2.
Compare and contrast the friction factor curves for flow in tubes and flow around spheres.
Why do they have different shapes?
3.
In Fig. 6.2-2, why does the
f
versus Re curve for turbulent flow lie above the curve for laminar
flow rather than below?
4.
Discuss the caveat after
Eq.
6.2-18.
Will the use of the mean hydraulic radius for laminar
flow
predict a pressure drop that is too high or too low for a given flow rate?
5.
Can friction factor correlations be used for unsteady flows?
6.
What is the connection, if any, between the Blake-Kozeny equation
(Eq.
6.4-9) and Darcy's
law
(Eq.
4C.3-2)?

Problems
193
7.
Discuss the flow of water through a 1/2-in. rubber garden hose that is attached to a house
faucet with a pressure of 70 psig available.
8.
Why was Eq. 6.4-12 rewritten in the form of Eq. 6.4-13?
9.
A
baseball announcer says: "Because of the high humidity today, the baseball cannot go as far
through the heavy humid air as it would on a dry day." comment critically on this statement.
PROBLEMS
6A.1
Pressure drop required for a pipe with fittings.
What pressure drop is needed for pumping water at 20°C
through a pipe of 25 cm diameter and 1234 m length at a
rate of 1.97 m3/s? The pipe is at the same elevation through-
out and contains four standard radius 90" elbows and two
45"
elbows. The resistance of a standard radius 90" elbow is
roughly equivalent to that offered by a pipe whose length is
32
diameters; a 45" elbow, 15 diameters. (An alternative
method for calculating losses in fittings is given in g7.5.)
Answer:
4.7
X
lo3
psi
=
33 MPa
(a)
Solve by Method A of Example 6.2-2.
(b)
Solve by Method
B
of Example 6.2-2.
Answer:
68
U.S.
gal/min
6A.4
Motion of a sphere in a liquid.
A hollow sphere,
5.00 mm
in
diameter, with a mass of 0.0500 g, is released in
a column of liquid and attains a terminal velocity of 0.500
cm/s. The liquid density is 0.900 g/cm3. The local gravita-
tional acceleration is 980.7 cm/sec2. The sphere is far
enough from the containing walls so that their effect can
be neglected.
(a)
Compute the drag force on the sphere in dynes.
(b)
Compute the friction factor.
(c)
Determine the viscosity of the liquid.
Answers:
(a)
8.7 dynes;
(b)
f
=
396;
(c)
3.7g/cm-s
6A.2
Pressure difference required for flow in pipe with
elevation change
(Fig. 6A.2). Water at 68OF is to be
pumped through 95 ft of standard 3-in. pipe (internal
di-
ameter 3.068 in.) into an overhead reservoir.
(a)
What pressure is required at the outlet of the pump to
6A.5
Sphere diameter for a given terminal velocity.
(a)
Explain how to find the sphere diameter
D
corre-
sponding to given values of
v,,
p, p,,
p,
and
g
by mak-
ing a direct construction on Fig. 6.3-1.
(b)
Rework Problem
2A.4
by
using Fig. 6.3-1.
(c)
Rework
(b)
when the gas velocity is
10
ft/s.
Fig.
6A.2.
Pipe flow system.
supply water to the overhead reservoir at a rate of 18
gal/min? At 68°F the viscosity of water is 1.002 cp and the
density is 0.9982 g/ml.
(b)
What percentage of the pressure drop is needed for
overcoming the pipe friction?
Answer:
(a)
15.2 psig
6A.3
Flow rate for a given pressure drop.
How many
gal/hr of water at 68°F can be delivered through a 1320-ft
length of smooth 6.00-in. i.d. pipe under a pressure differ-
ence of 0.25 psi? Assume that the pipe is "hydraulically
smooth.''
6A.6
Estimation of void fraction of a packed column.
A
tube of 146 sq. in. cross section and 73 in. height is
packed with spherical particles of diameter 2 mm. When a
pressure difference
of
158 psi is maintained across the col-
umn, a
60%
aqueous sucrose solution at 20°C flows
through the bed at a rate of 244 lb/min. At this tempera-
ture, the viscosity of the solution is 56.5 cp and its density
is 1.2865 g/cm3. What is the void fraction of the bed? Dis-
cuss the usefulness of this method of obtaining the void
fraction.
Answer:
0.30
6A.7
Estimation of pressure drops in annular flow.
For
flow in an annulus formed by cylindrical surfaces of diam-
eters
D
and
KD
(with
K
<
1) the friction factors
for
laminar
and turbulent flow are
Laminar
r-
Turbulent
&
=
G
log l,,(~eK@\/f)
-
H
194
Chapter 6 Interphase Transport in Isothermal Systems
in which the Reynolds number is defined by
Re,
=
K
D(l
-
K)(ZI,)~
P
(6A.7-3)
The values of
G,
H,
and
K
are given as:'
Equation 6A.7-2 is based on Problem 5C.2 and reproduces
the experimental data within about 3% up to Reynolds
numbers of 20,000.
(a) Vedy that, for developed laminar flow, Eqs. 6A.7-1 and
3 with the tabulated
K
values are consistent with
Eq.
2.4-16.
(b) An annular duct is formed from cylindrical surfaces of
diameters 6 in. and 15 in. It is desired to pump water at
60°F at a rate of 1500 cu ft per second. How much pressure
drop is required per unit length of conduit, if the annulus
is horizontal? Use
Eq.
6A.7-2.
(c)
Repeat (b) using the "mean hydraulic radius" empiri-
cism.
6A.8
Force on a water tower in
a
gale. A water tower
has a spherical storage tank 40 ft in diameter. In a 100-mph
gale what is the force of the wind on the spherical tank at
O°C?
Take the density of air to be 1.29 g/liter or 0.08 lb/ft3
and the viscosity to be 0.017 cp.
Answer:
1.7
X
1041bf
6A.9
Flow of gas through a packed column. A horizon-
tal tube with diameter 4 in. and length
5.5
ft is packed with
glass spheres of diameter 1/16 in., and the void fraction is
0.41. Carbon dioxide is to be pumped through the tube at
300K, at which temperature its viscosity is known to be
1.495
X
W4
g/cm
.
s. What will be the mass flow rate
through the column when the inlet and outlet pressures
are 25 atm and 3 atm, respectively?
Answer:
480 g/s
'
D.
M.
Meter
and
R.
B.
Bird,
AIChE
Journal,
7,4145
(1961).
6A.10
Determination of pipe diameter. What size of cir-
cular pipe is needed to produce a flow rate of 250 firkins
per fortnight when there is a pressure drop of
3
x
lo5
scru-
ples per square barleycorn? The pipe is horizontal. (The
authors are indebted to Professor
R.
S.
Kirk of the Univer-
sity of Massachusetts, who introduced them to these
units.)
6B.1
Effect of error in friction factor calculations. In
a
calculation using the Blasius formula for turbulent flow in
pipes, the Reynolds number used was too low by 4%. Cal-
culate the resulting error in the friction factor.
Answer:
Too high by 1%
6B.2
Friction factor for flow along a flat plate2
(a)
An expression for the drag force on a flat plate, wetted
on both sides, is given in Eq. 4.4-30. This equation was de-
rived by using
laminar
boundary layer theory and is
known to be in good agreement with experimental data.
Define a friction factor and Reynolds number, and obtain
the
f
versus Re relation.
(b) For
turbulent
flow, an approximate boundary layer treat-
ment based on the
1
/7 power velocity distribution gives
Fk
=
O.O~~~V~WL(LV,~/~)-~'~
(6B.2-1)
When 0.072 is replaced by 0.074, this relation describes the
drag force within experimental error for
5
X
lo5
<
Lv,plp.
<
2
x
lo7.
Express the corresponding friction factor as
a
function of the Reynolds number.
6B.3
Friction factor for laminar flow in a slit. Use the
results of Problem 2B.3 to show that for the laminar flow
in
a thin slit of thickness 2B the friction factor is
f
=
12/Re,
if
the Reynolds number is defined as Re
=
2B(vz)p/p.
Com-
pare this result for
f
with what one would get from the
mean hydraulic radius empiricism.
6B.4
Friction factor for a rotating disk.3 A thin circular
disk of radius
R
is immersed in a large body of fluid with
density p and viscosity
p.
If a torque
T,
is required to make
the disk rotate at an angular velocity
0,
then a friction fac-
tor
f
may be defined analogously to Eq. 6.1-1 as follows,
TJR
=
AKf
(6B.4-1)
where reasonable definitions for
K
and
A
are
K
=
ip(flRI2
and
A
=
2(77R2). An appropriate choice for the Reynolds
number for the system is Re
=
R2Qp/~.
For
laminar
flow, an exact boundary layer develop-
ment gives
T,
=
0.616~rp~~m (68.4-2)
-
--
-
H.
Schlichting,
Baud
y-Layer Theo
y,
McGraw-Hill,
New
York, 7th edition (1979),
Chapter
XXI.
T.
von
Kdrmkn,
Zeits.Fr
angew. Math.
u.
Mech.,
1,233-252
(1921).
Problems
195
For
turbulent
flow, an approximate boundary layer treat-
ment based on the 1
/7
power velocity distribution leads to
T,
=
0.073~Cl~~~~p,/ (6B.4-3)
Express these results as relations between
f
and Re.
6B.5
Turbulent flow in horizontal pipes. A fluid is
flowing with a mass flow rate
w
in
a
smooth horizontal
pipe of length
L
and diameter D as the result of a pressure
difference
po
-
pL.
The flow is known to be turbulent.
The pipe is to be replaced by one of diameter D/2 but
with the same length. The same fluid is to be pumped at
the same mass flow rate
w.
What pressure difference will
be needed?
(a)
Use Eq. 6.2-12 as a suitable equation for the friction factor.
(b) How can this problem be solved using Fig. 6.2-2 if Eq.
6.2-12
is not appropriate?
Answer:
(a)
A
pressure difference 27 times greater will be
needed.
6B.6
Inadequacy of mean hydraulic radius for laminar
flow.
(a)
For
laminar flow in an annulus with radii
KR
and
R,
use Eqs. 6.2-17 and 18 to get an expression for the average
velocity in terms of the pressure difference analogous to
the exact expression given in Eq. 2.4-16.
(b) What is the percentage of error in the result in (a) for
,(
=
l?
Answer:
49%
68.7
Falling sphere in Newton's drag-law region. A
sphere initially at rest at
z
=
0 falls under the influence of
gravity. Conditions are such that, after a negligible inter-
val, the sphere falls with a resisting force proportional to
the square of the velocity.
(a)
Find the distance
z
that the sphere falls as
a
function of t.
(b) What is the terminal velocity of the sphere? Assume
that
the density of the fluid is much less than the density of
the sphere.
Answer:
(a) The distance is
z
=
(l/c2g) In cosh cgt, where
c2
=
~(0.44)(p/ps& /gR); (b)
1
/c
68.8
Design of an experiment to verify the
f
vs.
Re
chart
for spheres. It is desired to design an experiment to test
the friction factor chart in Fig. 6.3-1 for flow around a
sphere. Specifically, we want to test the plotted value
f
=
1
at
Re
=
100. This is to be done by dropping bronze spheres
(psph
=
8
g/cm3) in water (p
=
1
g/cm3,
p
=
lop2
g/cm. s).
What sphere diameter must be used?
(a)
Derive a formula that gives the required diameter as
a
function of
f,
Re,
g,
p,
p, and pSph for terminal velocity
conditions.
(b)
Insert numerical values and find the value of the
sphere diameter.
3f Re2
p2
Answers:
(a)
D
=
3
(b)
D
=
0.048 cm
4(~
sph
-
P)P~'
r-
6B.9
Friction factor for flow past an infinite ~ylinder.~
The flow past a long cylinder is very different from the
flow past a sphere, and the method introduced in
g4.2
can-
not be used to describe this system. It is found that, when
the fluid approaches with a velocity
v,,
the kinetic force
acting on a length
L
of the cylinder is
The Reynolds number is defined here as Re
=
Dv,p/p.
Equation 6B.9-1 is valid only up to about Re
=
1.
In
this
range of Re, what is the formula for the friction factor as a
function of the Reynolds number?
6C.1
Two-dimensional particle trajectories. A sphere of
radius R is fired horizontally (in the
x
direction) at high ve-
locity in still air above level ground. As it leaves the pro-
pelling device, an identical sphere is dropped from the
same height above the ground (in the
y
direction).
(a) Develop differential equations from which the particle
trajectories can be computed, and that will permit compar-
ison of the behavior of the two spheres. Include the effects
of fluid friction, and make the assumption that steady-
state friction factors may be used (this is a "quasi-steady-
state assumption").
(b)
Which sphere will reach the ground first?
(c)
Would the answer to (b) have been the same if the
sphere Reynolds numbers had been in the Stokes' law
region?
dvx
3
vx
2
Pair
Answers: (a)
-
=
-s
i(
my
f
d
t
in
which
f
=
f(Re)
as
given by Fig.
5.3-1,
with
2~w~~~~
Re
=
Pair
6C.2
Wall effects for a sphere falling in a ~ylinder.~~
(a) Experiments on friction factors of spheres are generally
performed in cylindrical tubes. Show by dimensional
analysis that, for such an arrangement, the friction factor
for the sphere will have the following dependence:
f
=
f
(Re, R/Rcyl) (6C.2-1)
Here Re
=
2Rv,p/p, in which R is the sphere radius,
v,
is
the terminal velocity of the sphere, and RCy1 is the inside
G.
K.
Batchelor,
An Introduction to Fluid Dynamics,
Cambridge University Press
(1967),
pp.
244-246,257-261.
For
flow
past finite cylinders, see
J.
Happel and H. Brenner,
Low
Reynolds
Number
Hydrodynamics,
Martinus Nijhoff, The Hague
(19831,
pp.
227-230.
196
Chapter 6 Interphase Transport in Isothermal Systems
radius of the cylinder. For the
creeping flow
region, it has
been found empirically that the dependence off on R/RcYI
may be described by the
Ladenburg-Fax& correction?
so that
Wall effects for falling droplets have also been st~died.~
(b) Design an experiment to check the graph for spheres
in Fig. 6.3-1. Select sphere sizes, cylinder dimensions, and
appropriate materials for the experiment.
6C.3
Power input to an agitated tank (Fig. 6C.3). Show
by dimensional analysis that the power, P, imparted by a
rotating impeller to an incompressible fluid in an agitated
tank may be correlated, for any specific tank and impeller
shape, by the expression
P
2N
-
=
@(?,
E,
Nt)
(6C.3-1)
pN3D5
8
Here
N
is the rate of rotation of the impeller,
D
is the im-
peller diameter,
t
is the time since the start of the opera-
tion, and
@
is a function whose form has to be determined
experimentally.
For the commonly used geometry shown in the figure,
the power is given by the sum of two integrals represent-
ing the contributions of friction drag of the cylindrical tank
Impeller
Baffle
\
body and bottom and the form drag of the radial baffles,
respectively:
Here
T,
is the tohue required to turn the impeller,
S
is the
total surface area of the tank, A is the surface area of the
baffles, (considered positive on the "upstream" side and
negative on the "downstream side"),
X
is the radial
dis-
tance to any surface element dS or dA from the impeller
axis of rotation, and
n
is the distance measured normally
into the fluid from any element of tank surface dS.
The desired solution may now be obtained by dimen-
sional analysis of the equations of motion and continuity
by rewriting the integrals above in dimensionless form.
Here it is convenient to use D, DN, and
pp~2
for the char-
acteristic length, velocity, and pressure, respectively.
6D.1
Friction factor for a bubble in a clean liquid.'r8
When a gas bubble moves through a liquid, the bulk of
the
liquid behaves as if it were in potential flow; that is, the
flow field in the liquid phase is very nearly given by Eqs.
4B.5-2 and 3.
The drag force is closely related to the energy dissipa-
tion in the liquid phase (see Eq. 4.2-18)
Fkv,
=
E,
(6D.l-1)
Show that for irrotational flow the general expression
for
the energy dissipation can be transformed into the follow-
ing surface integral:
E,,
=
p$(n.
Vv2)
dS
(6D.1-2)
Next show that insertion of the potential flow velocity
pro-
files into
Eq.
6D.1-2, and use of
Eq.
6D.1-1 leads to
A
somewhat improved calculation that takes into account
the dissipation in the boundary layer and
in
the turbulent
Side view
wake leads to the following result:'
Top view
f=-
I---
:(
%)
(6D.1-4)
Fig.
6C.3.
Agitated tank with a six-bladed impeller and
four vertical baffles.
This result seems to hold rather well up to a Reynolds
number of about
200.
R.
Ladenburg,
Ann. Pkysik
(4),
23,447
(1907);
H.
FaxCn,
dissertation, Uppsala (1921). For extensive discussions of wall
effects for falling spheres,
see
J.
Happel and
H.
Brenner,
Low
L. Landau and
E.
M.
Lifshitz,
Fluid Mechanics,
Pergamon,
Reynolds Number Hydrodynamics,
Martinus Nijhoff, The Hague
Oxford (19871, pp. 182-183.
(1983).
G.
K.
Batchelor,
An Introduction
to
Fluid Dynamics,
J.
R.
Strom and
R.
C.
Kintner,
AICkE
Journal,
4,153-156
Cambridge University Press, (1963, pp. 367-370.
(1958).
D.
W.
Moore,
J.
Fluid Mech.,
16,
161-176 (1963).
