Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


55.2
Time-Smoothed Equations of Change for Incompressible Fluids
157
t
I
Time
t
Time
t
Fig.
5.2-1.
Sketch showing the velocity component
v,
as well as its time-smoothed value
&
and its fluctuation
v:
in turbulent flow
(a)
for "steadily driven turbulent flow" in which
&
does not depend on time, and
(b)
for a
situation in which
v
does depend on time.
the period to being long enough to give a smooth averaged function. For the system at
hand, the quantity
&,
which we call the time-smoothed velocity, is independent of time,
but of course depends on position. When the time-smoothed velocity does not depend
on time, we speak of steadily driven turbulent pow. The same comments we have made for
velocity can also be made for pressure.
Next we consider turbulent flow
in
a tube with a time-dependent pressure gradient.
For such a flow one can define time-smoothed quantities as above, but one has to under-
stand that the period
to
must be small with respect to the changes in the pressure gradi-
ent, but still large with respect to the periods of fluctuations. For such a situation the
time-smoothed velocity and the actual velocity are illustrated in Fig. 5.2-l(b).'
According to the definition in Eq. 5.2-2, it is easy to verify that the following rela-
tions are true:
The quantity
2
will not, however, be zero, and in fact the ratio
-/(8,)
can be taken to
be a measure of the magnitude of the turbulent fluctuations. This quantity, known as the
intensity of turbulence, may have values from 1 to 10% in the main part of a turbulent
stream and values of 25% or higher in the neighborhood of a solid wall. Hence, it must be
emphasized that we are not necessarily dealing with tiny disturbances; sometimes the fluc-
tuations are actually quite violent and large.
Quantities such as v,:.vi are also nonzero. The reason for this is that the local motions
in the
x
and y directions are correlated. In other words, the fluctuations in the
x
direction
are not independent of the fluctuations in the y direction. We shall see presently that
these time-smoothed values of the products of fluctuating properties have an important
role in turbulent momentum transfer. Later we shall find similar correlations arising in
turbulent heat and mass transport.
'
One can also define the "overbar" quantities in terms of an "ensemble average." For most
purposes the results are equivalent or are assumed to be
so.
See, for example,
A.
A.
Townsend,
The
Structure
of
Turbulent Shear
Flow,
Cambridge University Press, 2nd edition
(1976).
See also
P.
K.
Kundu,
Fluid
Mechanics,
Academic Press, New York
(1990),
p. 421, regarding the last of the formulas given in
Eq.
5.2-3.

158
Chapter
5
Velocity Distributions in Turbulent Flow
Having defined the time-smoothed quantities and discussed some of the properties
of the fluctuating quantities, we can now move on to the time-smoothing of the equations
of change. To keep the development as simple as possible, we consider here only the
equations for a fluid of constant density and viscosity. We start by writing the equations
of continuity and motion with
v
replaced by its equivalent
F
+
v'
and p by its equivalent
-
p
+
p'. The equation of continuity is then (V
.
v)
=
0, and we write the x-component of the
equation of motion, Eq. 3.5-6, in the d/dt form by using Eq. 3.5-5:
d
a
-
d
-
p(vx
+
v;)
=
--
(p
+
p')
-
p(v,
+
v:)(v,
+
v:)
+
P(V,
+
vpv,
+
v:)
d
t dx
dy
The y- and z-components of the equation of motion can be similarly written. We next
time-smooth these equations, making use of the relations given in Eq. 5.2-3. This gives
+
pV2E,
+
pg, (5.2-7)
dz
with similar relations for the y- and z-components of the equation of motion. These are
then the time-smoothed equations of continuity and motion for a fluid with constant density
and viscosity. By comparing them with the corresponding equations in Eq. 3.1-5 and
Eq. 3.5-6 (the latter rewritten in terms of d/dt), we conclude that
a.
The equation of continuity is the same as we had previously, except that
v
is now
replaced by
i.
b.
The equation of motion now has
i
and
p
where we previously had
v
and
p.
In
ad-
dition there appear the dashed-underlined terms, which describe the momentum
transport associated with the turbulent fluctuations.
We may rewrite Eq. 5.2-7 by introducing the turbulent momentum flux tensor
7'')
with
components
-
-
-
I
I
-
I
I
7;:)
=
pvxvx
T:
=
pvxvy
7:;)
=
Pm
and so on (5.2-8)
These quantities are usually referred to as the Reynolds stresses. We may also introduce
a
symbol
@"
for the time-smoothed viscous momentum flux. The components of this ten-
sor have the same appearance as the expressions given in Appendices B.l to
8.3,
except
that the time-smoothed velocity components appear in them:
This enables us then to write the equations of change in vector-tensor form as
(V
.
V)
=
0
and (V
.
v')
=
0 (5.2-10,ll)

s5.3
The Time-Smoothed Velocity Profile near a Wall
159
Equation 5.2-11 is an extra equation obtained by subtracting Eq. 5.2-10 from the original
equation of continuity.
The principal result of this section is that the equation of motion in terms of the
stress tensor, summarized in Appendix Table B.5, can be adapted for time-smoothed tur-
bulent flow by changing all
vi
to
Ei
and
p
to
P
as well as
T~
to
Tij
=
7:'
+
7;'
in any of the
coordinate systems given.
We have now arrived at the main stumbling block in the theory of turbulence.
The Reynolds stresses
7;'
above are not related to the velocity gradients in a simple
way as are the time-smoothed viscous stresses
7v
in Eq.
5.2-9.
They are, instead, com-
plicated functions of the position and the turbulence intensity. To solve flow prob-
lems we must have experimental information about the Reynolds stresses or else
resort to some empirical expression. In 55.4 we discuss some of the empiricisms that
are available.
Actually one can also obtain equations of change for the Reynolds stresses (see Prob-
111
lem 5D.1). However, these equations contain quantities like vivj vk. Similarly, the equa-
!
I
l
tions of change for the vivjvk contain the next higher-order correlation v,!v!v;v;, and so
on. That is, there is a never-ending hierarchy of equations that must be solved. To solve
flow problems one has to "truncate" this hierarchy by introducing empiricisms. If we
use empiricisms for the Reynolds stresses, we then have
a
"first-order" theory. If we in-
r
I
I
troduce empiricisms for the vivjv,, we then have a "second-order theory," and so on.
The problem of introducing empiricisms to get a closed set of equations that can be
solved for the velocity and pressure distributions is referred to as the "closure problem."
The discussion in 55.4 deals with closure at the first order. At the second order the
"k-E
empiricism" has been extensively studied and widely used in computational fluid
mechanics.'
55.3
THE TIME-SMOOTHED VELOCITY PROFILE NEAR A WALL
Before we discuss the various empirical expressions used for the Reynolds stresses, we
present here several developments that do not depend on any empiricisms. We are con-
cerned here with the fully developed, time-smoothed velocity distribution in the neigh-
borhood of a wall. We discuss several results: a Taylor expansion of the velocity near the
wall, and the universal logarithmic and power law velocity distributions a little further
out from the wall.
The flow near a flat surface is depicted in Fig. 5.3-1. It
is
convenient to distinguish
four regions of flow:
the viscous sublayer very near the wall, in which viscosity plays a key role
the buffer layer in which the transition occurs between the viscous and inertial
sublayers
the inertial sublayer at the beginning of the main turbulent stream, in which viscos-
ity plays at most a minor role
the main turbulent stream, in which the time-smoothed velocity distribution is
nearly flat and viscosity is unimportant
It must be emphasized that this classification into regions is somewhat arbitrary.
J.
L.
Lumley,
Adv. Appl.
Mech.,
18,123-176 (1978);
C.
G.
Speziale,
Ann.
Revs.
Fluid
Mech.,
23,
107-157 (1991);
H.
Schlichting and
K.
Gersten,
Bounda
y-Layer
Theoy,
Springer, Berlin, 8th edition (2000),
pp. 560-563.
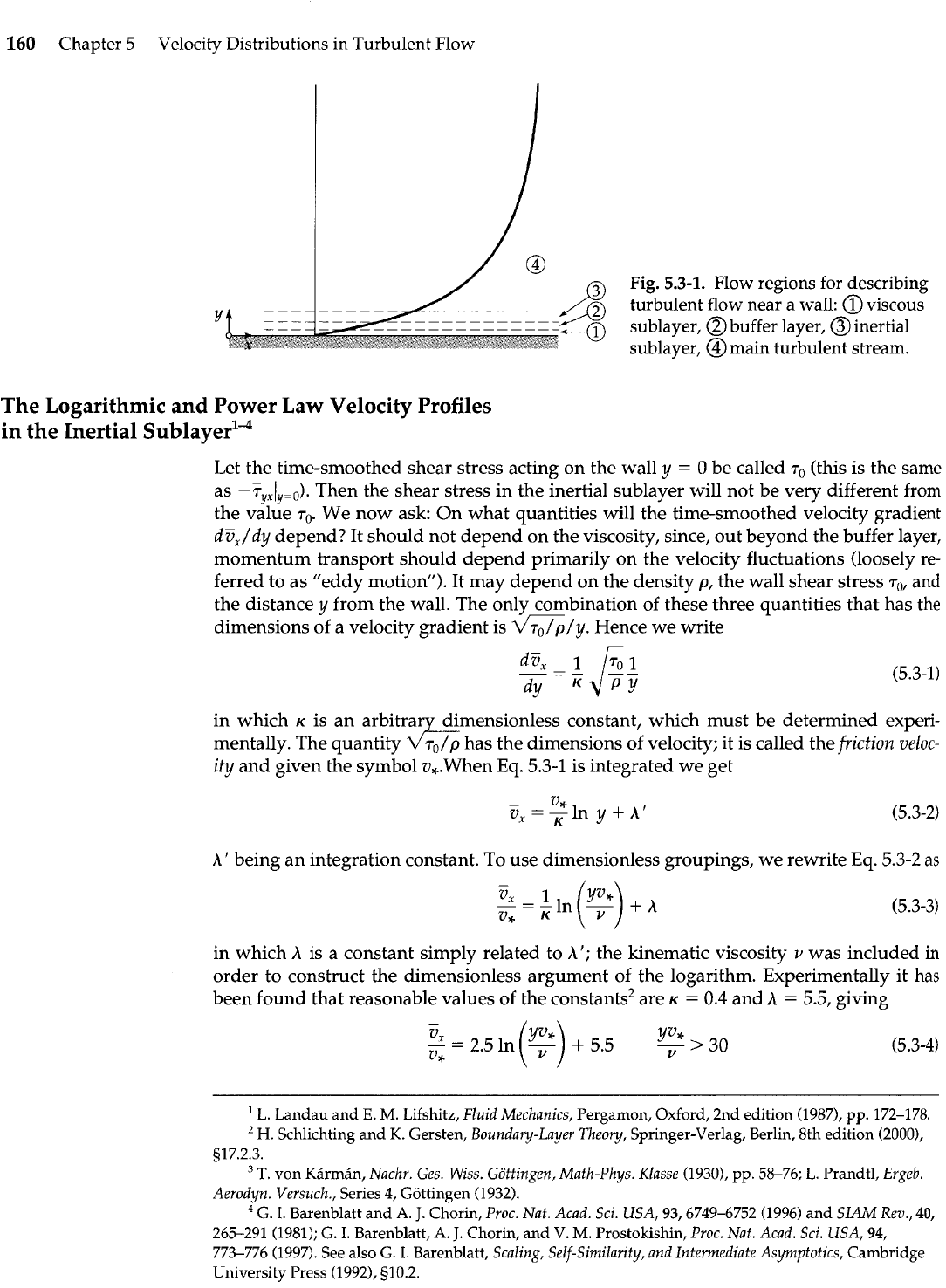
160
Chapter
5
Velocity Distributions in Turbulent Flow
Fig.
5.3-1.
Flow regions for describing
turbulent flow near a wall: @viscous
sublayer, @buffer layer, @inertial
sublayer,
@
main turbulent stream.
The Logarithmic and Power Law Velocity Profiles
in the Inertial Sublayer14
Let the time-smoothed shear stress acting on the wall
y
=
0
be called
7,
(this is the same
as
-7y.u)y=0).
Then the shear stress in the inertial sublayer will not be very different from
the value
7,.
We now ask: On what quantities will the time-smoothed velocity gradient
dv,/dy
depend? It should not depend on the viscosity, since, out beyond the buffer layer,
momentum transport should depend primarily on the velocity fluctuations (loosely re-
ferred to as "eddy motion"). It may depend on the density
p,
the wall shear stress
T,,,
and
the distance
y
from the wall. The only combination of these three quantities that has the
dimensions of a velocity gradient is
-ly.
Hence we write
-
in which
K
is an arbitra
dimensionless constant, which must be determined experi-
mentally. The quantity
3--
~,/p
has the dimensions of velocity; it is called the
friction
veloc-
ity
and given the symbol v,.When Eq. 5.3-1 is integrated we get
A'
being an integration constant. To use dimensionless groupings, we rewrite Eq. 5.3-2
as
in which
A
is a constant simply related to
A';
the kinematic viscosity
v
was included
in
order to construct the dimensionless argument of the logarithm. Experimentally it
has
been found that reasonable values of the constants2 are
K
=
0.4
and
A
=
5.5, giving
L. Landau and
E.
M.
Lifshitz,
Fluid Mechanics,
Pergamon, Oxford, 2nd edition (19871, pp. 172-178.
H.
Schlichting and
K.
Gersten,
Boundary-Layer Theory,
Springer-Verlag, Berlin, 8th edition (2000),
g17.2.3.
T.
von KBrmh,
Nachr. Ges. Wiss. Gottingen, Math-Phys. Klasse
(19301,
pp.
58-76;
L.
Prandtl,
Ergeb.
Aerodyn. Versuch.,
Series
4,
Gottingen (1932).
%.
I.
Barenblatt and
A.
J.
Chorin,
Proc. Nat. Acad. Sci. USA,
93,6749-6752 (1996) and
SIAM Rev.,
40,
265-291 (1981); G.
I.
Barenblatt,
A.
J.
Chorin, and V.
M.
Prostokishin,
Proc. Nat. Acad. Sci. USA,
94,
773-776 (1997). See also G.
I.
Barenblatt,
Scaling, Self-Similarity, and Intermediate Asymptotics,
Cambridge
University Press (1992), 510.2.
55.3
The Time-Smoothed Velocity Profile near a Wall
161
This is called the von Urmlin-Prandtl universal logarithmic velocity di~tribution;~ it is intended
to apply only in the inertial sublayer. Later we shall see (in Fig. 5.5-3) that this function
describes moderately well the experimental data somewhat beyond the inertial sublayer.
If Eq. 5.3-1 were correct, then the constants
K
and
h
would indeed be "universal con-
stants," applicable at any Reynolds number. However, values of
K
in the range 0.40 to
0.44 and values of
A
in the range 5.0 to
6.3
can be found in the literature, depending on
the range of Reynolds numbers. This suggests that the right side of Eq. 5.3-1 should be
multiplied by some function of Reynolds number and that
y
could be raised to some
power involving the Reynolds number. Theoretical arguments have been advanced4 that
Eq. 5.3-1 should be replaced by
in which
B,
=
ifi,
B,
=
y,
and
PI
=
z.
When Eq. 5.3-5 is integrated with respect to
y,
the
Barenblatt-Chorin universal velocity distribution is obtained:
Equation 5.3-6 describes regions @and
@of
Fig. 5.3-1 better than does Eq. 5.3-4.4 Region
a
is better described by Eq. 5.3-13.
Taylor-Series Development in the Viscous Sublayer
We start by writing a Taylor series for
E,
as a function of y, thus
To evaluate the terms in this series, we need the expression for the time-smoothed shear
stress in the vicinity of a wall. For the special case of the steadily driven flow in a slit of
-
thickness
2B,
the shear stress will be of the form
7,,
=
7::
+
7:;
=
-
~~[l
-
(y/B)I.
Then
from Eqs. 5.2-8 and
9,
we have
Now we examine one by one the terms that appear in Eq. 5.3-7:5
(i)
The first term is zero by the no-slip condition.
(ii)
The coefficient of the second term can be obtained from Eq. 5.3-8, recognizing
that both v: and
v;
are zero at the wall so that
(iii)
The coefficient of the third term involves the second derivative, which may be
obtained by differentiating Eq. 5.3-8 with respect to
y
and then setting
y
=
0, as follows,
2
(5.3-10)
dy
y=O
since both
vi
and
v;
are zero at the wall.
A. A.
Townsend,
The Structure
of
Turbulent Shear
Flow,
Cambridge University Press, 2nd edition
(1976),
p.
163.

162
Chapter
5
Velocity Distributions in Turbulent Flow
(iv)
The coefficient of the fourth term involves the third derivative, which may be
obtained from Eq. 5.3-8, and this is
Here Eq. 5.2-1
1
has been used.
There appears to be no reason to set the next coefficient equal to zero, so we find that
the Taylor series, in dimensionless quantities, has the form
The coefficient
C
has been obtained experimentally,' and therefore we have the final result:
The
y3
term in the brackets will turn out to be very important in connection with turbu-
lent heat and mass transfer correlations in Chapters 13,14,21, and 22.
For the region
5
<
yvJv
<
30 no simple analytical derivations are available, and
empirical curve fits are sometimes used. One of these is shown in Fig. 5.5-3 for circular
tubes.
55.4
EMPIRICAL EXPRESSIONS FOR THE
TURBULENT MOMENTUM FLUX
We
now return to the problem of using the time-smoothed equations of change in Eqs.
5.2-11 and 12 to obtain the time-smoothed velocity and pressure distributions. As
pointed out in the previous section, some information about the velocity distribution can
be obtained without having a specific expression for the turbulent momentum flux
F"'.
However, it has been popular among engineers to use various empiricisms for
I"'
that
involve velocity gradients. We mention a few of these, and many more can be found in
the turbulence literature.
The Eddy Viscosity of Boussinesq
By analogy with Newton's law of viscosity, Eq. 1.1-1, one may write for a turbulent shear
flow1
C.
5.
Lin,
R.
W.
Moulton, and
G.
L. Putnam,
Ind. Eng.
Chem.,
45,636-640 (1953); the numerical
coefficient was determined from mass transfer experiments in circular tubes. The importance of the
yj
term in heat and mass transfer was recognized earlier by
E.
V.
Murphree,
Ind.
Eng.
Chem.,
24,726-736
(1932). Eger Vaughn Murphree (1898-1962) was captain of the University of Kentucky football team in
1920 and became President of the Standard Oil Development Company.
'
J.
Boussinesq,
Mkm.
prks. par
diu.
savants
a
I'acad. sci,
de
Paris,
23,
#I, 1-680 (1877),24, #2,1-64 (1877).
Joseph Valentin Boussinesq (1842-19291, university professor in Lille, wrote a two-volume treatise on
heat, and is famous for the "Boussinesq approximation" and the idea of
"eddy
viscosity."

55.4
Empirical Expressions for the Turbulent Momentum Flux
163
in which
p"'
is the turbulent viscosity (often called the eddy viscosity, and given the
symbol
E).
As one can see from Table 5.1-1, for at least one of the flows given there,
the circular jet, one might expect
Eq.
5.4-1 to be useful. Usually, however,
p("
is a
strong function of position and the intensity of turbulence. In fact, for some systems2
p"'
may even be negative in some regions. It must be emphasized that the viscosity
p
is a property of the fluid, whereas the eddy viscosity
p"'
is primarily a property of
the flow.
For two kinds of turbulent flows (i.e., flows along surfaces and flows
in
jets and
wakes), special expressions for
p't'
are available:
(i)
Wall turbulence:
YV*
0<,<5
14.5~
This expression, derivable from Eq. 5.3-13, is valid only very near the wall. It is of con-
siderable importance in the theory of turbulent heat and mass transfer at fluid-solid
interface^.^
in which
K,
is a dimensionless coefficient to be determined experimentally,
b
is the
width of the mixing zone at a downstream distance
z,
and the quantity in parentheses
represents the maximum difference in the z-component of the time-smoothed veloci-
ties at that distance
z.
Prandt14 found Eq. 5.4-3 to be a useful empiricism for jets and
wakes.
The
Mixing
Length
of
Prandtl
By assuming that eddies move around in a fluid very much as molecules move around
in a low-density gas (not a very good analogy) prandt15 developed an expression for mo-
mentum transfer in a turbulent fluid. The "mixing length"
1
plays roughly the same role
as the mean free path in kinetic theory (see 51.4). This kind of reasoning led Prandtl to
the following relation:
If the mixing length were a universal constant, Eq. 5.4-4 would be very attractive, but in
fact
1
has been found to be a function of position. Prandtl proposed the following expres-
sions for
I:
(i)
Wall turbulence:
I
=
~,y
(y
=
distance from wall)
(ii)
Free turbulence:
I
=
~,b
(b
=
width of mixing zone)
in which
K,
and
KZ
are constants.
A
result similar to Eq. 5.4-4 was obtained by Taylor6 by
his "vorticity transport theory" some years prior to Prandtl's proposal.
J.
0.
Hinze,
Appl.
Sci. Res.,
22,163-175
(1970);
V.
Kruka
and
S.
Eskinazi,
J.
Fluid. Mech.,
20,555-579
(1964).
C.
S.
Lin,
R.
W.
Moulton,
and
G.
L.
Putnam,
Ind. Eng. Chem.,
45,636-640 (1953).
L. Prandtl,
Zeits.
f.
angew. Math. u. Mech.,
22,241-243 (1942).
L.
Prandtl,
Zeits.
f.
angew. Math. u. Mech.,
5,136-139
(1925).
G.
I.
Taylor,
Phil. Trans.
A215,l-26
(1915),
and
Proc. Roy. Soc.
(London), A135,685-701 (1932).

164
Chapter 5 Velocity Distributions in Turbulent Flow
The
Modified van
Driest
Equation
There have been numerous attempts to devise empirical expressions that can describe
the turbulent shear stress all the way from the wall to the main turbulent stream. Here
we give a modification of the equation of van Drie~t.~ This is a formula for the mixing
length of Eq.
5.4-4:
This relation has been found to be useful for predicting heat and mass transfer rates in
flow in tubes.
In the next two sections and in several problems at the end of the chapter, we illus-
trate the use of the above empiricisms. Keep in mind that these expressions for the
Reynolds stresses are little more than crutches that can be used for the representation of
experimental data or for solving problems that fall into rather special classes.
Obtain an expression for
7:;
=
pv:vi
as
a
function of
y
in the neighborhood of the wall.
Development of the
SOLUTION
Reyno Ids Stress
Expression in the
(a)
We
start by making a Taylor series development of the three components of
v':
Vicinity of
the
Wall
The first term in Eqs. 5.4-8 and 10 must be zero because of the no-slip condition; the first term
in Eq.
5.4-9
is zero in the absence of mass transfer. Next we can write Eq. 5.2-11 at
y
=
0,
The first and third terms in this equation are zero because of the no-slip condition. Therefore
we have to conclude that the second term is zero as well. Hence all the dashed-underlined
terms in Eqs. 5.4-8 to
10
are zero, and we may conclude that
-
$j?
=
PD:Z'j.
=
AY3
+
BY4
+
*
. .
(5.4-12)
This suggests-but does not proves-that the lead term
in
the Reynolds stress near a wall
should be proportional to
y3.
Extensive studies of mass transfer rates in closed channels9 have,
however, established that
A
f
0.
E.
R. van Driest,
J.
Aero.
Sci.,
23,1007-1011 and 1036 (1956). Van Driest's original equation did
not have the square root divisor. This modification was made
by
0.
T. Hanna,
0.
C.
Sandall, and
P.
R.
Mazet,
AIChE Journal,
27,693-697 (1981) so that the turbulent viscosity would be proportional to
as
y
+
0,
in accordance with Eq. 5.4-2.
H.
Reichardt,
Zeits.
f.
angew.
Math.
u. Mech.,
31,20&219 (1951). See also
J.
0.
Hinze,
Turbulence,
McGraw-Hill, New York,
2nd
edition (1975),
pp.
620-621.
R.
H. Notter and
C. A.
Sleicher,
Chem. Eng.
Sci.,
26,161-171 (1971);
0.
C.
Sandal1 and
0.
T. Hanna,
AIChE
Journal,
25,190-192 (1979); D.
W.
Hubbard and
E.
N.
Lightfoot,
Ind. Eng. Chem. Fundamentals,
5,
370-379 (1966).
s5.5
Turbulent Flow in Ducts
165
(b)
For the flow between parallel plates, we can use the expression found in
Eq.
5.3-12 for the
time-smoothed velocity profile to get the turbulent momentum flux:
where
A
=
~C(V,/U)~. This is in accord with
Eq.
5.4-12.
55.5
TURBULENT
FLOW
IN
DUCTS
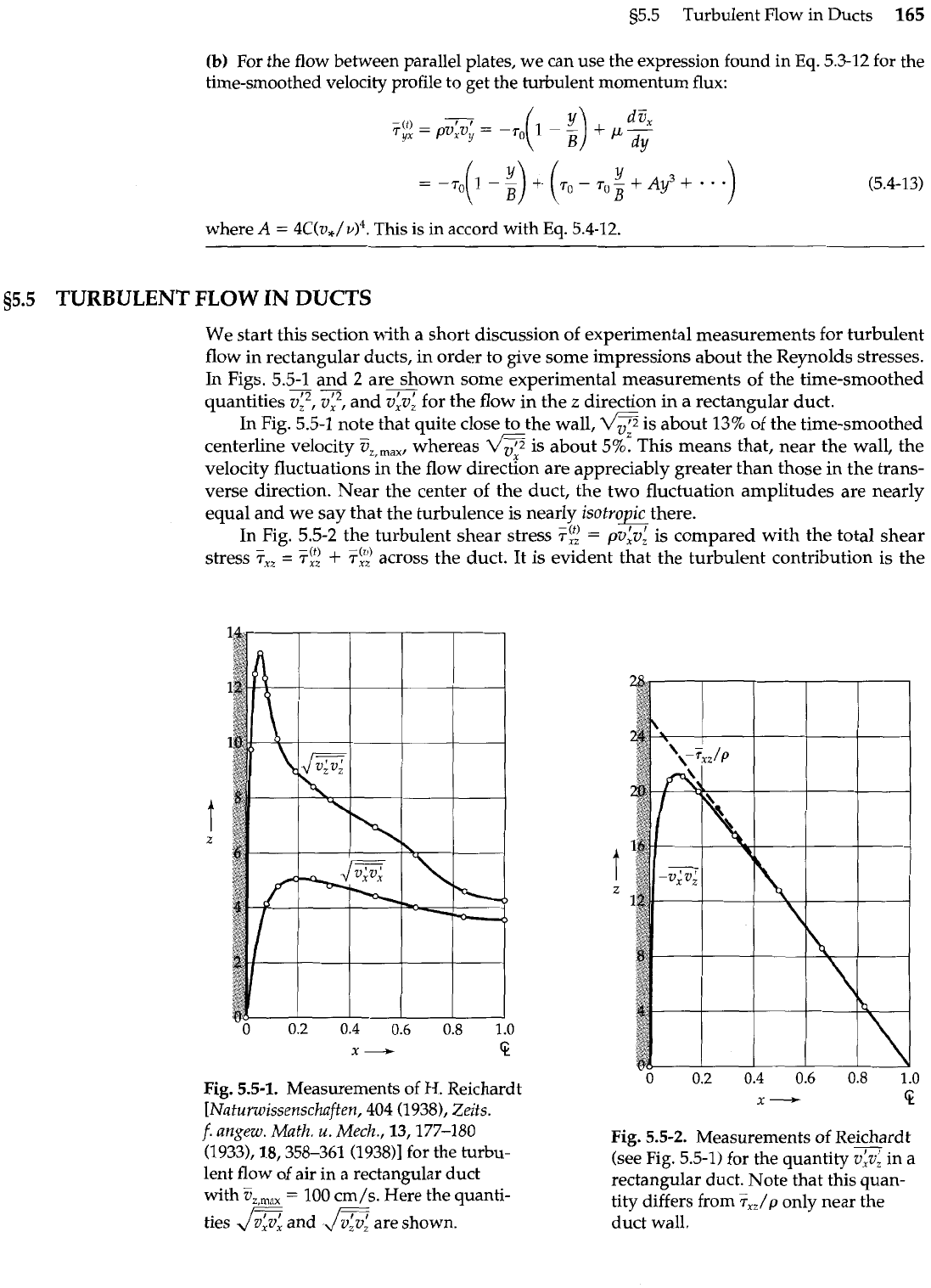
We start this section with a short discussion of experimental measurements for turbulent
flow in rectangular ducts, in order to give some impressions about the Reynolds stresses.
In
Figs.
5.5-1
--
and
2
are
-
shown some experimental measurements of the time-smoothed
quantities vL2,
v:~,
and v:vi for the flow in the
z
direction in a rectangular duct.
In Fig. 5.5-1 note that quite close to the wall,
is about
13%
of the time-smoothed
centerline velocity
Z,,,,,,
whereas
is about 5%. This means that, near the wall, the
velocity fluctuations in the flow direction are appreciably greater than those in the trans-
verse direction. Near the center of the duct, the two fluctuation amplitudes are nearly
equal and we say that the turbulence is nearly isotro~there.
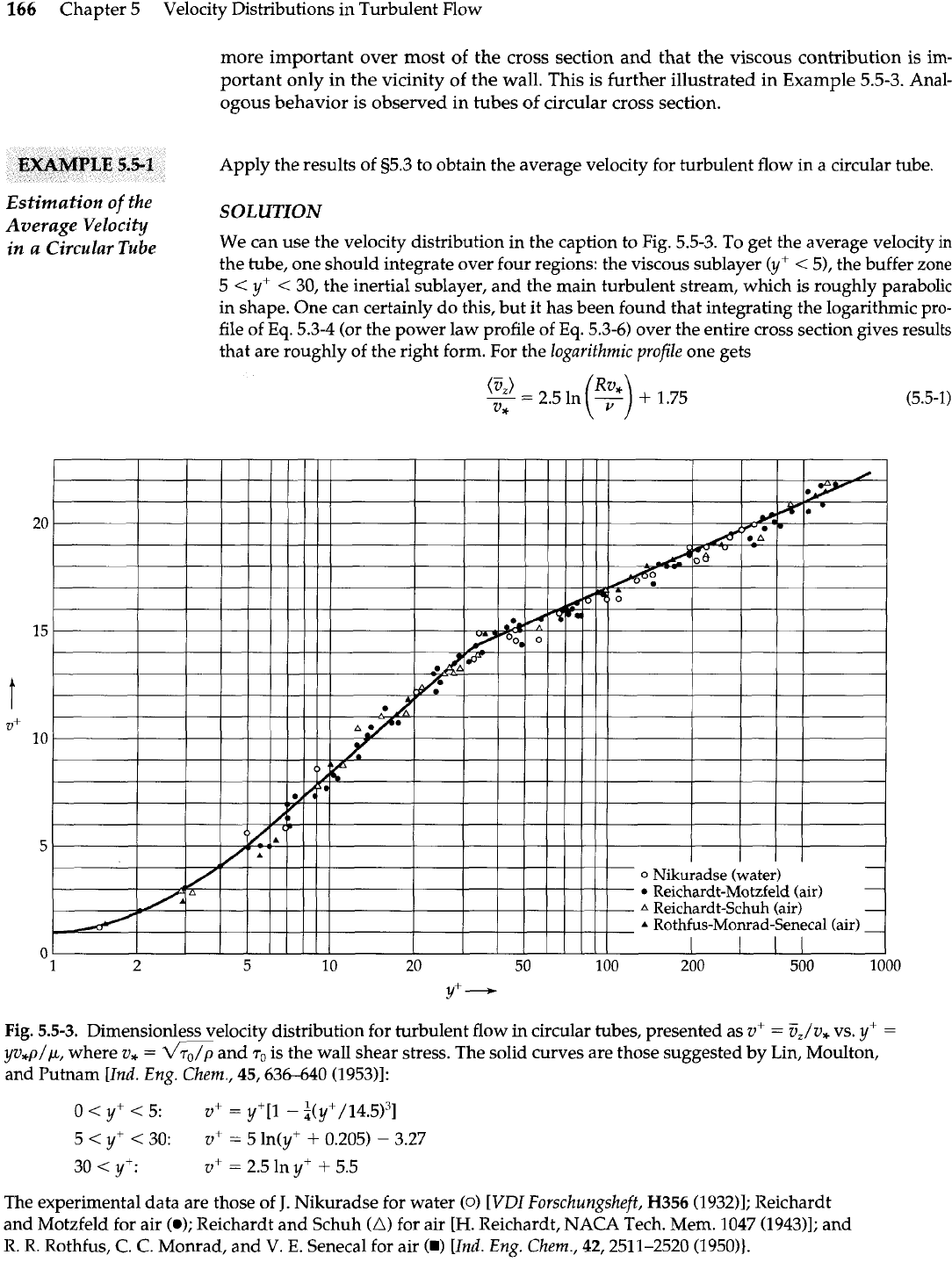
In
Fig. 5.5-2 the turbulent shear stress
7:;
=
p:v;
is compared with the total shear
stress 7,,
=
7:;
+
7:?
across the duct.
It
is evident that the turbulent contribution is the
Fig.
5.5-1. Measurements
of
H.
Reichardt
[Naturwissensckaften,
404
(1938),
Zeits.
f.
angew.
Math.
u.
Mech., 13,177-180
(1933), 18,358-361 (1938)l for the turbu-
lent flow of air in a rectangular duct
with
?&,,
=
100
cm/s. Here the quanti-
ties
a
and
a
are shown.
Fig.
5.5-2.
Measurements of Reichardt
(see Fig. 5.5-1) for the quantity in a
rectangular duct. Note that this quan-
tity differs from ?,,/p only near the
duct wall.
166
Chapter
5
Velocity Distributions in Turbulent Flow
more important over most of the cross section
and
that the viscous contribution
is
im-
portant only in the vicinity of the wall. This is further illustrated in Example
5.5-3.
Anal-
ogous behavior is observed in tubes of circular cross section.
Apply the results of
95.3
to obtain the average velocity for turbulent flow in a circular tube.
Estimation of
the
Average Velocity
SOLUTION
in a Circular Tube
We can use the velocity distribution in the caption to Fig.
5.5-3.
To get the average velocity in
the tube, one should integrate over four regions: the viscous sublayer
(y+
<
51,
the buffer zone
5
<
y+
<
30,
the inertial sublayer, and themain turbulent stream; which
is
roughly parabolic
in shape. One can certainly do this, but it has been found that integrating the logarithmic pro-
file of
Eq.
5.3-4
(or the power law profile of
Eq.
5.3-6)
over the entire cross section gives results
that are roughly of the right form. For the logarithmic profile one gets
Fig.
5.5-3.
Dimensionless velocity distribution for turbulent flow
in
circular tubes, presented as
vf
=
5,/u,
vs.
y+
=
yv,p/~,
where
v,
=
and
.r,
is the wall shear stress. The solid curves are those suggested by Lin, Moulton,
and Putnam [Ind. Eng. Chem.,
45,636-640 (1953)l:
The experimental data are those of
J.
Nikuradse for water
(0)
[VDI Forschungsheft,
H356
(1932)l;
Reichardt
and Motzfeld for air
(0);
Reichardt and Schuh
(A)
for air
[H.
Reichardt,
NACA
Tech. Mem.
1047 (1943)l;
and
R.
R.
Rothfus,
C.
C.
Monrad, and
V.
E.
Seneca1 for air
(H)
[Ind. Eng. Chem.,
42,2511-2520 (1950)).
