Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

Problems

147

and phase. The amplitude ratio (ratio of amplitude of output function to input function) and

phase shift both depend on the viscosity of the fluid and hence can be used for determining

the viscosity. It is assumed throughout that the oscillations are of small amplitude. Then the

problem is a linear one, and it can

solved either by Laplace transform or by the method

outlined in this problem.

(a)

First, apply Newton's second law of motion to the cylindrical bob for the special case that

the annular space is completely evacuated. Show that the natural frequency of the system is

l/iTTI, in which I is the moment of inertia of the bob, and

is the spring constant for the

torsion wire.

(b)

Next, apply Newton's second law when there is a fluid of viscosity

in the annular

space. Let

be the angular displacement of the bob at time

and

be the tangential velocity

of the fluid as a function of

and t. Show that the equation of motion of the bob is

If the system starts from rest, we have the initial conditions

I.C.:

att=O,

OR=O

and

-=O

(4C.2-2)

(c)

Next, write the equation of motion for the fluid along with the relevant initial and bound-

ary conditions:

(Fluid)

LC.:

B.C.

R--

(4C.2-5)

B.C. 2: at

aR,

do,,

aR-

(4C.2-6)

The function

OaR(t)

is a specified sinusoidal function (the "input"). Draw a sketch showing

OQR

and

as functions of time, and defining the amplitude ratio and the phase shift.

(d)

Simplify the starting equations, Eqs. 4C.2-1 to

by making the assumption that a is only

slightly greater than unity, so that the curvature may be neglected (the problem can be solved

without making this assumption4). This suggests that a suitable dimensionless distance vari-

able is

R)/[(a

1)Rl. Recast the entire problem in dimensionless quantities in such

way that

/o,

is used as a characteristic time, and so that the viscosity appears in just

one dimensionless group. The only choice turns out to be:

time:

(4C.2-7)

velocity:

viscosity:

2.rrR4Lp(a

reciprocal of moment of inertia:

Markovitz,

Appl.

Phys.,

23,1070-1077 (1952)

has solved the problem without assuming

small spacing between

the

cup and bob. The cup-and-bob instrument has been used by

Wittenberg,

Ofte, and

Curtiss,

Chem.

Phys.,

48,3253-3260 (1968),

to measure the viscosity of liquid

plutonium alloys.

148

Chapter

Velocity Distributions with More Than One Independent Variable

Show that the problem can now be restated as follows:

(bob)

(fluid)

From these two equations we want to get 6, and

as functions of x and 7, with

and

parameters.

(e)

Obtain the "sinusoidal steady-state" solution by taking the input function

BQR

(the dis-

placement of the cup) to be of the form

in which

@/on

wV!%

is a dimensionless frequency. Then postulate that the bob and

fluid motions will also be sinusoidal, but with different amplitudes and phases:

%{6ieiGr] (6; is complex)

(4C.2-14)

4(~,

%(40(x)e~Z;7)

is complex) (4C.2-15)

Verify that the amplitude ratio is given by

IB;J

/6&, where

.I indicates the absolute magni-

tude of a complex quantity. Further show that the phase angle

is given

tan

3{0i{/M{Bf;j, where

and

stand for the real and imaginary parts, respectively.

(f)

Substitute the postulated solutions of (e) into the equations in (d) to obtain equations for

the complex amplitudes 6hnd 4".

(g)

Solve the equation for +"(XI and verify that

(h)

Next, solve the 6; equation to obtain

from which the amplitude ratio

lBil

/6iR and phase shift

can be found.

(i)

For high-viscosity fluids, we can seek a power series by expanding the hyperbolic func-

tions in Eq. 4C.2-17 to get a power series in 1 /M. Show that this leads to

From this, find the amplitude ratio and the phase angle.

(j)

Plot l6;l /6iR versus

for p/p

10 cm2/s,

25 cm,

5.5

cm,

2500 gm/cm2,

lo6

dyn cm. Where is the maximum in the curve?

4C.3

Darcy's equation for flow through porous media.

For the flow of a fluid through a porous

medium, the equations of continuity and motion may be replaced by

smoothed continuity equation

-(V

pvo)

(4C.3-1)

Darcy's equation5

(Vp

pg)

(4C.3-2)

Henry

Philibert

Gaspard Darcy

(1803-1858) studied in Paris and became famous for designing

the municipal water-supply system in Dijon, the city of his birth.

Darcy,

Les Fontaines Publiques de la

Ville de Dijon,

Victor Dalmont, Paris (1856). For further discussions of "Darcy's law," see

Happel and

Brenner,

Low Reynolds Number Hydrodynamics,

Martinus Nihjoff, Dordrecht (1983); and

Brenner

and D.

Edwards,

Macrofransporf Processes,

Butterworth-Heinemann, Boston (1993).

Problems

149

in which

the porosity, is the ratio of pore volume to total volume, and

is the permeability of

the porous medium. The velocity

in these equations is the superficial velocity, which is de-

fined as the volume rate of flow through a unit cross-sectional area of the solid plus fluid, av-

eraged over a small region of space-small with respect to the macroscopic dimensions in the

flow system, but large with respect to the pore size. The density and pressure are averaged

over a region available to flow that is large with respect to the pore size. Equation 4C.3-2 was

proposed empirically to describe the slow seepage of fluids through granular media.

When Eqs. 4C.3-1 and

are combined we get

for constant viscosity and permeability. This equation and the equation of state describe the

motion of a fluid in a porous medium. For most purposes we may write the equation of state as

in which

p,,

is the fluid density at unit pressure, and the following parameters have been given:6

Incompressible liquids m=O p=O

Compressible liquids

m=O

pfO

Isothermal expansion of gases

Adiabatic expansion of gases

C,/Cp

Show that Eqs. 4C.3-3 and 4 can be combined and simplified for these four categories to give

(for gases it is customary to neglect the gravity terms since they are small compared with the

pressure terms):

Case 1.

V28

(4C.3-5)

Case 2.

Case 3.

Case 4.

Note that Case

leads to Laplace's equation, Case

without the gravity term leads to the heat-

conduction or diffusion equation, and Cases 3 and 4 lead to nonlinear

equation^.^

4C.4

Radial flow through a porous

medium

(Fig. 4C.4).

fluid flows through

porous cylindri-

cal shell with inner and outer radii R, and R,, respectively. At these surfaces, the pressures

are known to be p, and p,, respectively. The length of the cylindrical shell is

Porous medium Fluid

---

fZL----7;i--+

mass

.-+

J--

rate of

flow

----

------

Fig.

4C.4.

Radial flow

through a porous

Pressure

medium.

M. Muskat,

Flow of Homogeneous Fluids Through Porous Media,

McGraw-Hill(1937).

For the boundary condition at a porous surface

that

bounds a moving fluid, see

Beavers and

Joseph,

Fluid Mech.,

30,197-207 (1967) and

S. Beavers,

M. Sparrow, and

Masha,

AIChE

Journal,

20,596-597 (1974).

150

Chapter

Velocity Distributions with More Than One Independent Variable

(a) Find the pressure distribution, radial flow velocity, and mass rate of flow for an incom-

pressible fluid.

(b) Rework (a) for a compressible liquid and for an ideal gas.

ln (r/RJ

zm~h(p2

p1)p

Answers: (a)

vOr

In (R,/R,) Pr In (R2/Rl)

In (R2/R,)

4D.1 Flow near an oscillating wa1L8 Show, by using Laplace transforms, that the complete solu-

tion to the problem stated in Eqs. 4.1-44 to 47 is

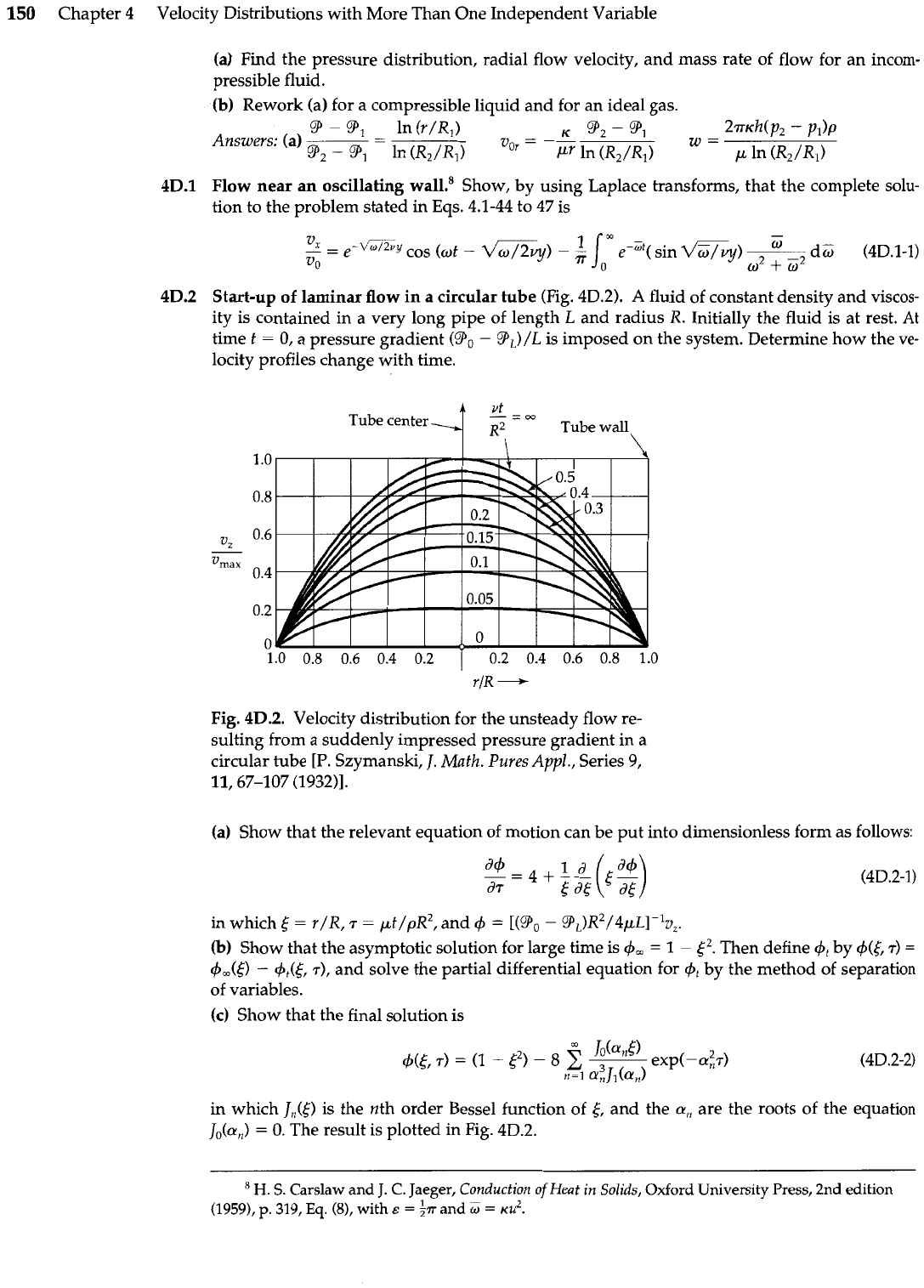
4D.2 Start-up of laminar flow in a circular tube (Fig. 4D.2).

fluid of constant density and viscos-

ity is contained in a very long pipe of length

and radius R. Initially the fluid is at rest.

time

a pressure gradient (Yo

YL)/L is imposed on the system. Determine how the

ve-

locity profiles change with time.

Tube center

Tube wall

Fig. 4D.2. Velocity distribution for the unsteady flow re-

sulting from a suddenly impressed pressure gradient in a

circular tube

[P.

Szymanski,

Math. Pures Appl., Series 9,

11,67-107 (1932)l.

(a) Show that the relevant equation of motion can be put into dimensionless form as follows:

in which

?/A,

pt/pR2, and

[(Yo

9L)R2/4pLl-'v,.

(b) Show that the asymptotic solution for large time is

t2. Then define

+((,

+m(t)

+r(e,

r), and solve the partial differential equation for

by the method of separation

of variables.

(c)

Show that the final solution is

in which J,@ is the nth order Bessel function of t, and the

are the roots of the equation

Jo(an)

0. The result is plotted in Fig. 4D.2.

Carslaw and

Jaeger,

Conduction of

Heat

in Solids,

Oxford University

Press,

2nd

edition

(1959),

319,

Eq.

(a),

with

$.rr

and

KU'.

Problems

151

Fig.

4D.3.

Rotating disk in a circular tube.

Flows in the disk-and-tube system

(Fig. 4D.3):

(a)

A fluid in a circular tube is caused to move tangentially by a tightly fitting rotating disk at

the liquid surface at z

0; the bottom of the tube is located at

Find the steady-state veloc-

ity distribution v&r, z), when the angular velocity of the disk is

Assume that creeping flow

prevails throughout, so that there is no secondary flow. Find the limit of the solution as

(b)

Repeat the problem for the unsteady flow. The fluid is at rest before t

0, and the disk

suddenly begins to rotate with an angular velocity at t

Find the velocity distribution

vJr,

t) for a column of fluid of height

Then find the solution for the limit as

(c)

If the disk is oscillating sinusoidally in the tangential direction with amplitude

a,,

obtain

the velocity distribution in the tube when the "oscillatory steady state" has been attained. Re-

peat the problem for a tube of infinite length.

Unsteady annular flows.

(a)

Obtain a solution to the Navier-Stokes equation for the start-up of

axial

annular flow by a

sudden impressed pressure gradient. Check your result against the published s~lution.'~

(b)

Solve the Navier-Stokes equation for the unsteady

tangential

flow in an annulus. The fluid

is at rest for

Starting at

the outer cylinder begins rotating with a constant angular

velocity to cause laminar flow for

Compare your result with the published solution."

Stream functions for three-dimensional flow.

(a)

Show that the velocity functions pv

and pv

[(V+')

(V+JI

both satisfy the

equation of continuity identically for steady flow. The functions

+,,

+*,

and A are arbitrary,

except that their derivatives appearing in

pv) must exist.

(b)

Show that the expression A/p

S3+/h3

reproduces the velocity components for the four

incompressible flows of Table 4.2-1. Here

is the scale factor for the third coordinate (see

5A.7).

(Read the general vector v of

Eq.

A.7-18 here as A.)

(c)

Show that the streamlines of [(Vfi,)

(Vfi2)I are given by the intersections of the surfaces

rCI,

constant and

fi2

constant. Sketch such a pair of surfaces for the flow in Fig. 4.3-1.

(d)

Use Stokes' theorem

(Eq.

A.5-4)

to obtain an expression in terms of

for the mass flow

rate through a surface

bounded by a closed curve

Show that the vanishing of v on

does

not imply the vanishing of

Hort,

Z. tech.

Phys.,

10,213 (1920);

Hill,

Huppler,

and

Bird,

Chem. Engr. Sci.,

21,

815-817 (1966).

Miiller,

Zeits. fur angew. Math.

Mech.,

16,227-228 (1936).

Bird and

Curtiss,

Chem.

Engr.

Sci,

11,108-113 (1959).

Chapter

Velocity Distributions

in Turbulent Flow

5.1 Comparisons of laminar and turbulent flows

55.2

Time-smoothed equations of change for incompressible fluids

55.3

The time-smoothed velocity profile near a wall

55.4 Empirical expressions for the turbulent momentum flux

55.5 Turbulent flow in ducts

55.6' Turbulent flow in jets

In the previous chapters we discussed laminar flow problems only. We have seen that

the differential equations describing laminar flow are well understood and that, for

number of simple systems, the velocity distribution and various derived quantities can

be obtained in a straightforward fashion. The limiting factor in applying the equations

change is the mathematical complexity that one encounters in problems for which there

are several velocity components that are functions of several variables. Even there, with

the rapid development of computational fluid dynamics, such problems are gradually

yielding to numerical solution.

In this chapter we turn our attention to turbulent flow. Whereas laminar flow is

orderly, turbulent flow is chaotic. It is this chaotic nature of turbulent flow that poses

all sorts of difficulties.

fact, one might question whether or not the equations

change given in Chapter

are even capable of describing the violently fluctuating

mo-

tions in turbulent flow. Since the sizes of the turbulent eddies are several orders

magnitude larger than the mean free path of the molecules of the fluid, the equations

of change

are

applicable. Numerical solutions of these equations are obtainable and

can be used for studying the details of the turbulence structure. For many purposes,

however, we are not interested in having such detailed information, in view of the

computational effort required. Therefore, in this chapter we shall concern ourselves

primarily with methods that enable us to describe the time-smoothed velocity and

pressure profiles.

s5.1

we start by comparing the experimental results for laminar and turbulent

flows in several flow systems. In this way we can get some qualitative ideas about the

main differences between laminar and turbulent motions. These experiments help to de-

fine some of the challenges that face the fluid dynamicist.

55.2

we define several

fime-smoothed

quantities, and show how these definitions

can be used to time-average the equations of change over a short time interval. These

equations describe the behavior of the time-smoothed velocity and pressure. The time-

smoothed equation of motion, however, contains the

turbulent momentum flux.

This

flux

Velocity Distributions in Turbulent How

153

cannot be simply related to velocity gradients in the way that the momentum flux is

given by Newton's law of viscosity in Chapter

At the present time the turbulent mo-

mentum flux is usually estimated experimentally or else modeled by some type of em-

piricism based on experimental measurements.

Fortunately, for turbulent flow near a solid surface, there are several rather general

results that are very helpful in fluid dynamics and transport phenomena: the Taylor se-

ries development for the velocity near the wall; and the logarithmic and power law ve-

locity profiles for regions further from the wall, the latter being obtained by dimensional

reasoning. These expressions for the time-smoothed velocity distribution are given in

s5.3.

In the following section, 55.4, we present a few of the empiricisms that have been

proposed for the turbulent momentum flux. These empiricisms are of historical interest

and have also been widely used in engineering calculations. When applied with proper

judgment, these empirical expressions can be useful.

The remainder of the chapter is devoted to a discussion of two types of turbulent

flows: flows in closed conduits (55.5) and flows in jets

(55.6).

These flows illustrate the

two classes of flows that are usually discussed under the headings of

wall turbulence

and

free turbulence.

In this brief introduction to turbulence we deal primarily with the description of the

fully developed turbulent flow of an incompressible fluid. We do not consider the theo-

retical methods for predicting the inception of turbulence nor the experimental tech-

niques devised for probing the structure of turbulent flow. We also give no discussion of

the statistical theories of turbulence and the way in which the turbulent energy is distrib-

uted over the various modes of motion. For these and other interesting topics, the reader

should consult some of the standard books on turbulence.l4 There is a growing litera-

ture on experimental and computational evidence for "coherent structures" (vortices) in

turbulent flows.7

Turbulence is an important subject. In fact, most flows encountered in engineering

are turbulent and not laminar! Although our understanding of turbulence is far from sat-

isfactory, it is a subject that must be studied and appreciated. For the solution to indus-

trial problems we cannot get neat analytical results, and, for the most part, such

problems are attacked by using a combination of dimensional analysis and experimental

data. This method is discussed in Chapter

Corrsin, "Turbulence: Experimental Methods," in

Handbuch der Physik,

Springer, Berlin (19631,

Vol. VIII/2. Stanley Corrsin (1920-1986), a professor at The Johns Hopkins University, was an excellent

experimentalist and teacher; he studied the interaction between chemical reactions and turbulence and

the propagation of the double temperature correlations.

Townsend,

The Structure of Turbulent Shear Flow,

Cambridge University Press, 2nd edition

(1976); see also

A. A.

Townsend in

Handbook

Fluid Dynamics

(V. L. Streeter, ed.), McGraw-Hill(1961)

for a readable survey.

J. 0. Hinze,

Turbulence,

McGraw-Hill, New York, 2nd edition (1975).

H. Tennekes and J.

Lumley,

First Course in Turbulence,

MIT Press, Cambridge, Mass. (1972);

Chapters 1 and 2 of this book provide an introduction to the physical interpretations of turbulent flow

phenomena.

Lesieur,

La Turbulence,

Presses Universitaires de Grenoble (1994); this book contains beautiful

color photographs of turbulent flow systems.

Several books that cover material beyond the scope of this text are:

McComb,

The Physics of

Fluid Turbulence,

Oxford University Press (1990); T.

Faber,

Fluid Dynamics for Physicists,

Cambridge

University Press (1995); U. Frisch,

Turbulence,

Cambridge University Press (1995).

Holmes,

Lumley, and

Berkooz,

Turbulence, Coherent Structures, Dynamical Systems, and

Symmetry,

Cambridge University Press (1996);

Waleffe,

Phys. Rev. Lett.,

81,41404148 (1998).

154

Chapter

Velocity Distributions in Turbulent Flow

5.1

COMPARISONS OF LAMINAR AND TURBULENT FLOWS

Before discussing any theoretical ideas about turbulence, it is important to summarize

the differences between laminar and turbulent flows in several simple systems. Specifi-

cally we consider the flow in conduits of circular and triangular cross section, flow along

a flat plate, and flows in jets. The first three of these were considered for laminar flow in

52.3, Problem 3B.2, and 54.4.

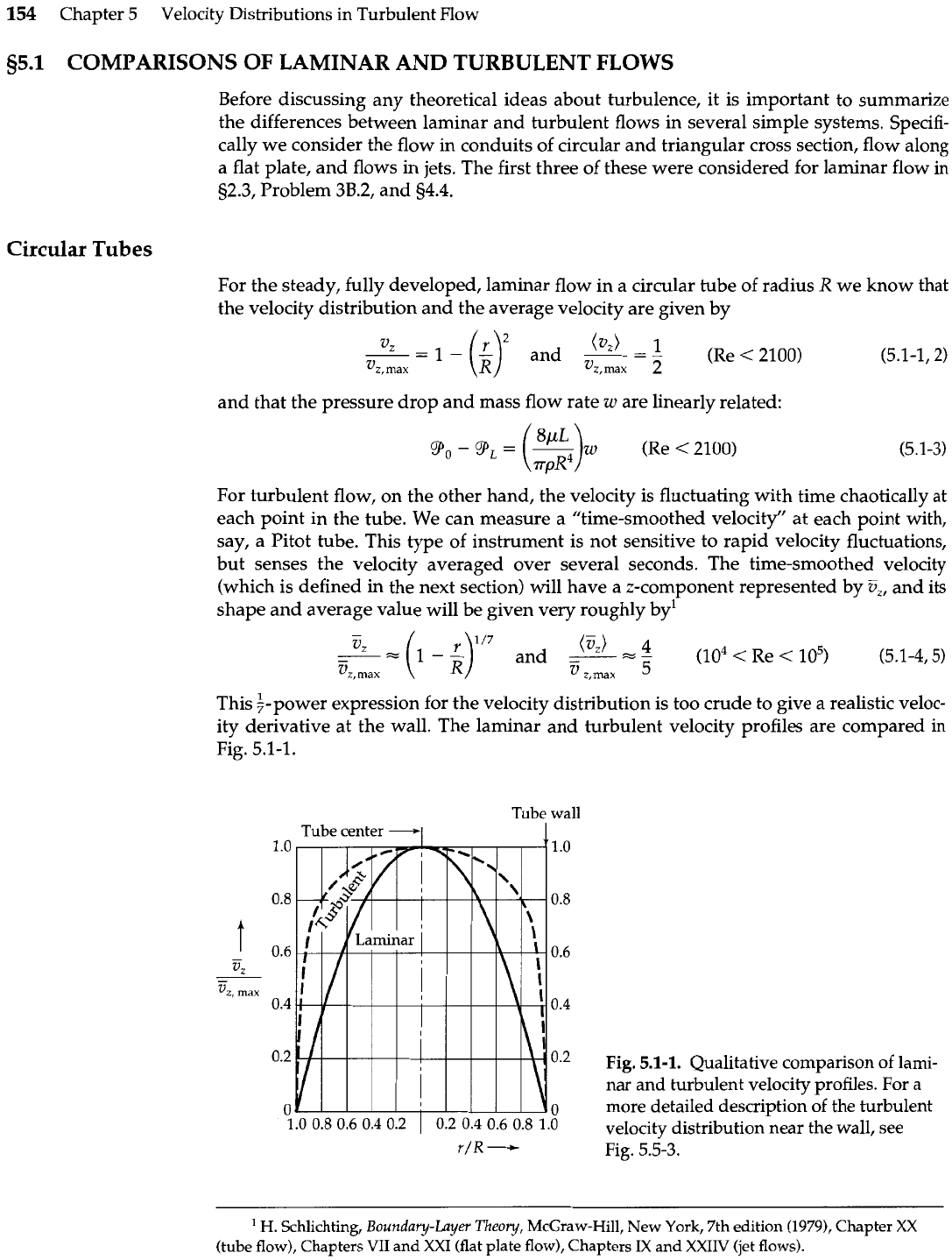
Circular Tubes

For the steady, fully developed, laminar flow in a circular tube of radius

we know that

the velocity distribution and the average velocity are given by

(a)

and

()

- -

(Re

2100)

Vz,

ma, Vz,max

and that the pressure drop and mass flow rate

are linearly related:

For turbulent flow, on the other hand, the velocity is fluctuating with time chaotically at

each point in the tube. We can measure a "time-smoothed velocity" at each point with,

say, a Pitot tube. This type of instrument is not sensitive to rapid velocity fluctuations,

but senses the velocity averaged over several seconds. The time-smoothed velocity

(which is defined in the next section) will have a z-component represented by

and its

shape and average value will be given very roughly by1

This $-power expression for the velocity distribution is too crude to give a realistic veloc-

ity derivative at the wall. The laminar and turbulent velocity profiles are compared in

Fig. 5.1-1.

Tube wall

Fig.

5.1-1.

Qualitative comparison of lami-

nar and turbulent velocity profiles. For a

more detailed description of the turbulent

10 0.8 0.6 0.4 0.2

0.2 0.4 0.6

0-8

1.0

velocity distributionnear the wall, see

r/R

Fig. 5.5-3.

Schlichting,

Boundary-Layer

Theory,

McGraw-Hill, New York, 7th edition

(1979),

Chapter XX

(tube flow), Chapters VII and XXI (flat plate flow), Chapters IX and XXIIV (jet flows).

5.1

Comparisons of Laminar and Turbulent Flows

155

Over the same range of Reynolds numbers the mass rate of flow and the pressure

drop are no longer proportional but are related approximately by

The stronger dependence of pressure drop on mass flow rate for turbulent flow results

from the fact that more energy has to be supplied to maintain the violent eddy motion in

the fluid.

The laminar-turbulent transition in circular pipes normally occurs at a

critical

Reynolds number of roughly 2100, although this number may be higher if extreme care is

taken to eliminate vibrations in the system.' The transition from laminar flow to turbu-

lent flow can be demonstrated by the simple experiment originally performed by

Reynolds. One sets up a long transparent tube equipped with a device for injecting a

small amount of dye into the stream along the tube axis. When the flow is laminar, the

dye moves downstream as a straight, coherent filament. For turbulent flow, on the other

hand, the dye spreads quickly over the entire cross section, similarly to the motion of

particles in Fig. 2.0-1, because of the eddying motion (turbulent diffusion).

Noncircular Tubes

For developed laminar flow in the triangular duct shown in Fig. 3B.2(b), the fluid parti-

cles move rectilinearly in the

direction, parallel to the walls of the duct. By contrast, in

turbulent flow there is superposed on the time-smoothed flow in the

direction (the

pri-

may

pow)

a time-smoothed motion in the xy-plane (the secondary flow). The secondary

flow is much weaker than the primary flow and manifests itself as

set of six vortices

arranged in a symmetric pattern around the duct axis (see Fig. 5.1-2). Other noncircular

tubes also exhibit secondary flows.

Flat

Plate

s4.4

we found that for the laminar flow around a flat plate, wetted on both sides, the

solution of the boundary layer equations gave the drag force expression

1.328-

(laminar)

Re,

lo5

(5.1-7)

in which ReL

Lvmp/,x

is the Reynolds number for a plate of length

the plate width is

and the approach velocity of the fluid is

v,.

Fig.

5.1-2.

Sketch showing the secondary flow patterns

for turbulent flow in a tube of triangular cross section

[H.

Schlichting, Bounda y-Layer

Theo

McGraw-Hill,

New York, 7th edition (1979), p.

6131.

Reynolds,

Phil.

Trans.

Roy.

Soc.,

174,

Part 111,935-982 (1883). See also

Draad and

Nieuwstadt,

Fluid

Mech.,

361,297-308 (1998).

156

Chapter

Velocity Distributions in Turbulent Flow

Table

5.1-1

Dependence of Jet Parameters on Distance

from Wall

Laminar flow Turbulent flow

Width Centerline

Mass Width Centerline Mass

of jet velocity

flow rate of jet

velocity flow rate

Circular jet

zpl

z-I

Plane jet

z2/3 z-~/3 =1/3

=-1/2

For turbulent flow, on the other hand, the dependence on the geometrical and phys-

ical properties is quite different:'

0.74~p4p~4~5v~

(turbulent) (5

10'

ReL

lo7)

(5.1-8)

Thus the force is proportional to the $-power of the approach velocity for laminar flow,

but to the $power for turbulent flow. The stronger dependence on the approach velocity

reflects the extra energy needed to maintain the irregular eddy motions in the fluid.

Circular and Plane Jets

Next we examine the behavior of jets that emerge from a flat wall, which is taken to

the xy-plane (see Fig. 5.6-1). The fluid comes out from a circular tube or a long narrow

slot, and flows into a large body of the same fluid. Various observations on the jets can

be made: the width of the jet, the centerline velocity of the jet, and the mass flow rate

through a cross section parallel to the xy-plane. All these properties can be measured as

functions of the distance

from the wall. In Table 5.1-1 we summarize the properties

the circular and two-dimensional jets for laminar and turbulent flow.' It is curious that,

for the circular jet, the jet width, centerline velocity, and mass flow rate have exactly the

same dependence on

in both laminar and turbulent flow. We shall return to this point

later in

55.6.

The above examples should make it clear that the gross features of laminar and

tur-

bulent flow are generally quite different. One of the many challenges in turbulence the-

ory is to try to explain these differences.

55.2

TIME-SMOOTHED EQUATIONS OF CHANGE

FOR INCOMPRESSIBLE FLUIDS

We begin by considering a turbulent flow in a tube with a constant imposed pressure

gradient. If at one point in the fluid we observe one component of the velocity as a func-

tion of time, we find that it is fluctuating in a chaotic fashion as shown

Fig. 5.2-l(a).

The fluctuations are irregular deviations from a mean value. The actual velocity can be

regarded as the sum of the mean value (designated by an overbar) and the fluctuation

(designated by a prime). For example, for the z-component of the velocity we write

which is sometimes called the Reynolds decomposition. The mean value is obtained from

v,(t)

by making a time average over a large number of fluctuations