Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

s5.5 Turbulent Flow in Ducts

167

If this is compared with experimental data on flow rate versus pressure drop, it is found that

good agreement can be obtained by changing 2.5 to 2.45 and 1.75 to 2.0. This "fudging" of the

constants would probably not be necessary if the integration over the cross section had been

done by using the local expression for the velocity in the various layers. On the other hand,

there is some virtue in having

simple logarithmic relation such as Eq. 5.5-1 to describe pres-

sure drop vs. flow rate.

In a similar fashion the

power law profile

can be integrated over the entire cross section to

give (see Ref.

of 95.3)

in which

3/(2 In Re). This relation is useful over the range 3.07

lo3

3.23

lo6.

Show how Eqs.

5.4-4

and

can be used to describe turbulent flow in a circular tube.

Application of SOLUTION

Prandtl's Mixing

Length

Formula to

Equation 5.2-12 gives for the steadily driven flow in a circular tube,

Turbulent Flow in a

Circular Tube

in which

Tr,

7:'

72.

Over most of the tube the viscous contribution is quite small; here we

neglect it entirely. Integration of Eq. 5.5-3 then gives

where

is the wall shear stress and

is the distance from the tube wall.

According to the mixing length theory in Eq.

5.4-4,

with the empirical expression in

Eq.

5.4-5, we have for

EJdr

negative

Substitution of this into Eq. 5.5-4 gives a differential equation for the time-smoothed velocity.

If we follow Prandtl and extrapolate the inertial sublayer to the wall, then in

Eq.

5.5-5 it is ap-

propriate to replace

75;

70.

When this is done, Eq. 5.5-5 can be integrated to give

constant

(5.5-6)

Thus

logarithmic profile is obtained and hence the results from Example 5.5-1 can be used;

that is, one can apply Eq. 5.5-6 as a very rough approximation over the entire cross section of

the tube.

Determine the ratio

p't'/p

R/2 for water flowing at a steady rate in a long, smooth,

round tube under the following conditions:

Relative Magnitude of

Viscosity and Eddy

tube radius

3 in.

7.62 cm

Viscosity

wall shear stress

2.36

lop5

1bf/in.'

0.163 Pa

density

62.4 lb,/ft3

1000 kg/m3

kinematic viscosity

1.1

lop5

ft2/s

1.02

lop7

m2/s

SOLUTION

The expression for the time-smoothed momentum flux is

168

Chapter

Velocity Distributions in Turbulent Flow

This result may be solved for

p'f'/p

and the result can be expressed in terms of dimensionless

variables:

,p)

7rz

El. El.

dE,/dy

where

yv,p/~

and

&/v,.

When

R/2,

the value of

For this value of yt, the logarithmic distribution in the caption of Fig. 5.5-3 gives

Substituting this into

Eq.

5.5-8 gives

This result emphasizes that, far from the tube wall, molecular momentum transport is negli-

gible in comparison with eddy transport.

g5.6

TURBULENT

FLOW

JETS

In the previous section we discussed the flow in ducts, such as circular tubes; such flows

are examples of

wall

turbulence.

Another main class of turbulent flows is

free turbulence,

and the main examples of these flows are jets and wakes. The time-smoothed velocity in

these types of flows can be described adequately by using Prandtl's expression for the

eddy viscosity in Fig.

5.4-3,

or by using Prandtl's mixing length theory with the empiri-

cism given in

Eq.

5.4-6.

The former method is simpler, and hence we use it in the follow-

ing illustrative example.

jet of fluid emerges from a circular hole into a semi-infinite reservoir of the same fluid as

depicted in Fig. 5.6-1.

the same figure we show roughly what we expect the profiles

Time-Smoothed

the z-component of the velocity to look like. We would expect that for various values of

Distribution in

the profiles will be similar in shape, differing only by a scale factor for distance and veloc-

a Circular Wall

JeP4

ity. We also can imagine that as the jet moves outward, it will create a net radial inflow so

that some of the surrounding fluid will be dragged along. We want to find the time-

smoothed velocity distribution in the jet and also the amount of fluid crossing each plane

constant

Before working through the solution, it may be useful to review the information

on jets in Table 5.1-1.

H. Schlichting,

Boundary-Layer Theory,

McGraw-Hill, New York, 7th edition (19791, pp. 747-750.

Townsend,

The Structure of Turbulent Shear Flow,

Cambridge University Press, 2nd edition

(19761, Chapter 6.

9.0.

Hinze,

Turbulence,

McGraw-Hill, New York, 2nd edition (1975), Chapter 6.

Goldstein,

Modern Developments

Fluid Dynamics,

Oxford University Press (1938), and Dover

reprint (1965), pp. 592-597.

55.6 Turbulent Flow in Jets

169

SOLUTION

Circular

hole

Fig.

5.6-1.

Circular jet

emerging from a plane

wall.

In order to use Eq. 5.4-3 it is necessary to know how

and

q,,,,

v,,,

vary with

for the cir-

cular jet. We know that the total rate of flow of z-momentum

will be the same for all values

We presume that the convective momentum flux is much greater than the viscous mo-

mentum flux. This permits us to postulate that the jet width

depends on J, on the density p

and the kinematic viscosity

of the fluid, and on the downstream distance z from the wall.

The only combination of these variables that has the dimensions of length is

~z/~v~, so

that the jet width is proportional to

We next postulate that the velocity profiles are "similar," that is,

which seems like a plausible proposal; here

is the velocity along the centerline. When

this is substituted into the expression for the rate of momentum flow in the jet (neglecting the

contribution from

7,,)

we find that

Since J does not depend on

and since

is proportional to z, then

G,,,,,

has to be inversely

proportional to

The

&,,,

in Eq.

5.4-3

occurs at the outer edge of the jet and is zero. Therefore because

z and

fi,,,,

z-', we find from

Eq.

5.4-3

that

/L(')

is a constant. Thus we can use the equations

of motion for laminar flow and replace the viscosity

the eddy viscosity

p(t),

dt).

In the jet the main motion is in the z direction; that is

< <

Hence we can use a

boundary layer approximation (see

54.4)

for the time-smoothed equations of change and write

continuity:

motion:

These equations are to be solved with the following boundary conditions:

B.C.

The last boundary condition is automatically satisfied, inasmuch as we have already found

that

%,,,,

is inversely proportional to z. We now seek a solution to Eq. 5.6-5 of the form of

Eq.

5.6-1 with

170

Chapter 5 Velocity Distributions in Turbulent Flow

To avoid working with two dependent variables, we introduce the stream function

discussed in

g.2.

For axially symmetric flow, the stream function is defined as follows:

This definition ensures that the equation of continuity in

Eq.

5.6-4 is satisfied. Since we know

that

z-'

some function of

we deduce from Eq. 5.6-9 that

must be proportional to

Furthermore

must have dimensions of (velocity)

(length)2, hence the stream function

must have the form

in which

is a dimensionless function of

r/z.

From Eqs. 5.6-9 and

then get

The first two boundary conditions may now be rewritten as

B.C. 1:

at[=O, --F1=O

(5.6-14)

B.C.

ate=0,

we expand

in a Taylor series about

then the first boundary condition gives a

0, and the second gives

We will use this

result presently.

Substitution of the velocity expressions of Eqs. 5.6-12 and 13 into the equation of motion

Eq. 5.6-5 then gives a third-order differential equation for

This may be integrated to give

FF' F'

-=FU--+C,

in which the constant of integration must be zero; this can be seen by using the Taylor series

in Eq. 5.6-16 along with the fact that a, b, and

are all zero.

Equation

5.6-18

was first solved by Schlichting.' First one changes the independent vari-

able by setting

The resulting second-order differential equation contains only the de-

pendent variable and its first two derivatives. Equations of this type can be solved

elementary methods. The first integration gives

Once again, knowing the behavior of

near

(

we conclude that the second constant of in-

tegration is zero. Equation 5.6-19 is then a first-order separable equation, and it may

solved

to give

Schlichting,

Zeits.

angew.

Math.

Mech.,

13,260-263

(1933).

g5.6 Turbulent Flow

Jets

171

which

is the third constant of integration. Substitution of this into Eqs. 5.6-12 and 13

then gives

When the above expression for

is substituted into Eq. 5.6-2 for J, we get an expression for

the third integration constant in terms of

The last three equations then give the time-smoothed velocity profiles in terms of J,

and

v"'.

measurable quantity in jet flow is the radial position corresponding to an axial velocity

one-half the centerline value; we call this half-width

b,,,.

From

Eq.

5.6-21 we then obtain

Experiments indicate6 that

blI2

0.08482.

When this is inserted into

Eq.

5.6-24, it is found that

15.1. Using this value, we can get the turbulent viscosity

v"'

as a function of

and

from

Eq. 5.6-23.

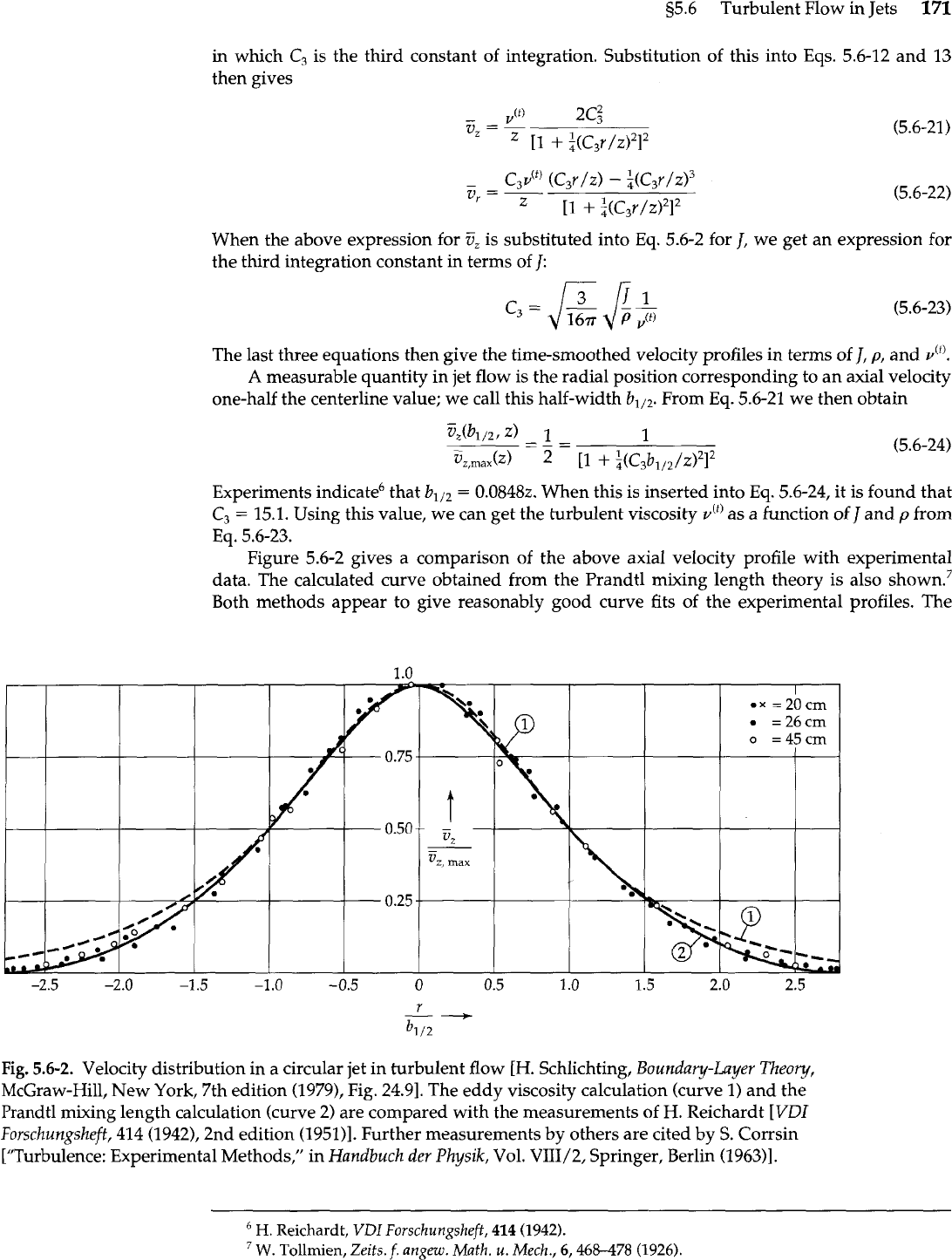
Figure 5.6-2 gives a comparison of the above axial velocity profile with experimental

data. The calculated curve obtained from the Prandtl mixing length theory is also shown.7

Both methods appear to give reasonably good curve fits of the experimental profiles. The

Fig.

5.6-2.

Velocity distribution in a circular jet in turbulent flow

[H.

Schlichting,

Boundary-Layer

Theory,

McGraw-Hill, New York, 7th edition (1979), Fig. 24.91. The eddy viscosity calculation (curve

and the

Prandtl mixing length calculation (curve 2) are compared with the measurements of

Reichardt

[VDI

Forschungsheft,

414 (1942), 2nd edition (1951)l. Further measurements by others are cited by

Corrsin

["Turbulence: Experimental Methods," in

Handbuch der

Physik,

Vol. VIII/2 Springer, Berlin (1963)l.

Reichardt,

VDI

Forschungsheft,

414

(1942).

Tollmien,

Zeifs.

angew.

Math.

Mech.,

6,468478

(1926).

172

Chapter 5 Velocity Distributions in Turbulent Flow

Fig.

5.6-3.

Streamline pattern in a circular jet in

turbulent flow

[H.

Schlichting, Bounda y-Layer

The-

ory,

McGraw-Hill, New York, 7th edition (1979),

Fig. 24.101.

eddy viscosity method seems to be somewhat better in the neighborhood of the maximum,

whereas the mixing length results are better in the outer part of the jet.

Once the velocity profiles are known, the streamlines can be obtained. From the stream-

lines, shown in Fig. 5.6-3, it can be seen how the jet draws in fluid from the surrounding mass

of fluid. Hence the mass of fluid carried by the jet increases with the distance from the source.

This mass rate of flow is

This result corresponds to an entry in Table 5.1-1.

The two-dimensional jet issuing from a thin slot may be analyzed sirnilarily. In that prob-

lem, however, the turbulent viscosity is a function of position.

QUESTIONS FOR DISCUSSION

Compare and contrast the procedures for solving laminar flow problems and turbulent flow

problems.

Why must Eq. 5.1-4 not be used for evaluating the velocity gradient at the solid boundary?

What does the logarithmic profile of Eq. 5.3-4 give for the fluid velocity at the wall? Why does

this not create a problem in Example 5.5-1 when the logarithmic profile is integrated over the

cross section of the tube?

Discuss the physical interpretation of each term in Eq. 5.2-12.

Why is the absolute value sign used in

Eq.

5.4-4? How is it eliminated in Eq. 5.5-5?

In Example 5.6-1, how do we know that the momentum flow through any plane of constant

is a constant? Can you imagine a modification of the jet problem in which that would not be

the case?

Go through some of the volumes of Ann. Revs. Fluid

Mech.

and summarize the topics in turbu-

lent flow that are found there.

In Eq. 5.3-1 why do we investigate the functional dependence of the velocity gradient rather

than the velocity itself?

Why is turbulence such a difficult topic?

PROBLEMS

5A.1

Pressure drop needed for laminar-turbulent transition.

fluid with viscosity 18.3 cp and

density 1.32 g/cm3 is flowing in a long horizontal tube of radius 1.05 in. (2.67 cm). For what

pressure gradient will the flow become turbulent?

Answer: 26 psi/mi (1.1

lo5

Pa/krn)

Problems

173

5A.2

Velocity distribution in turbulent pipe flow. Water is flowing through a long, straight, level

run of smooth 6.00 in. i.d. pipe, at a temperature of

68°F.

The pressure gradient along the

length of the pipe is 1.0 psi/mi.

(a) Determine the wall shear stress

in psi (lbf/in.2) and Pa.

(b) Assume the flow to be turbulent and determine the radial distances from the pipe wall at

which?&/^,,,,

0.0,0.1,0.2,0.4,0.7,0.85,1.0.

(c)

Plot the complete velocity profile,

i&/&,,,,

vs.

(d)

the assumption of turbulent flow justified?

(e) What is the mass flow rate?

5B.1

Average flow velocity in turbulent tube flow.

(a) For the turbulent flow in smooth circular tubes, the function'

is sometimes useful for curve-fitting purposes: near Re

lo3,

6; near

1.1

los,

and near Re

3.2

lo6,

10. Show that the ratio of average to maximum velocity is

and verify the result in

Eq.

5.1-5.

(b) Sketch the logarithmic profile in

Eq.

5.3-4 as a function of

when applied to

circular

tube of radius

Then show how this function may be integrated over the tube cross section

to get

Eq.

5.5-1. List all the assumptions that have been made to get this result.

58.2

Mass flow rate in a turbulent circular jet.

(a) Verify that the velocity distributions in Eqs. 5.6-21 and 22 do indeed satisfy the differen-

tial equations and boundary conditions.

(b) Verify that

Eq.

5.6-25 follows from

Eq.

5.6-21.

5B.3

The eddy viscosity expression in the viscous sublayer. Verify that

Eq.

5.4-2 for the eddy vis-

cosity comes directly from the Taylor series expression in

Eq.

5.3-13.

5C.1

Two-dimensional turbulent jet. A fluid jet issues forth from a slot perpendicular to the

xy-

plane and emerges

the

direction into a semi-infinite medium of the same fluid. The width

of the slot in the

direction is

Follow the pattern of Example 5.6-1 to find the time-

smoothed velocity profiles in the system.

(a) Assume the similar profiles

Show that the momentum conservation statement leads to the fact that the centerline velocity

must be proportional to

z-'/*.

(b) Introduce a stream function

such that

-d+/dx and

+d+/dz. Show that the re-

sult in (a) along with dimensional considerations leads to the following form for

Here

F(5)

is a dimensionless stream function, which will be determined from the equation of

motion for the fluid.

H. Schlichting,

Boundary-Layer

Theory,

McGraw-Hill, New York,

7th

edition

(1979),

pp.

596-600.

174

Chapter 5 Velocity Distributions in Turbulent How

(c)

Show that

Eq.

5.4-2 and dimensional considerations lead to the following form for the tur-

bulent kinematic viscosity:

Here

is a dimensionless constant that has to be determined from experiments.

(d)

Rewrite the equation of motion for the jet using the expression for the turbulent kine-

matic viscosity from (c) and the stream function from (b). Show that this leads to the follow-

ing differential equation:

For the sake of convenience, introduce a new variable

and rewrite

Eq.

5C.1-4.

(e) Next vedy that the boundary conditions for

Eq.

5C.1-4 are

F(0)

F1'(0)

and

Ff(~)

(f)

Show that

Eq.

5C.1-4 can be integrated to give

SF'

constant

(5C.1-6)

and that the boundary conditions require that the constant be zero.

(g)

Show that further integration leads to

where

is a constant of integration.

(h)

Show that another integration leads to

-C

tanh

(5C. 1

-8)

and that the axial velocity can be found from this to be

(i) Next show that putting the axial velocity into the expression for the total momentum of

the jet leads to the value

$'%

for the integration constant. Rewrite

Eq.

5C.1-9 in terms

rather than

The value of

0.0102 gives good agreement with the experimental data.'

The agreement is believed to be slightly better than that for the Prandtl mixing length

empiricism.

(j)

Show that the mass flow rate across any line

constant is given by

5C.2

Axial turbulent

flow

in an annulus. An annulus is bounded by cylindrical walls at

and

(where

1). Obtain expressions for the turbulent velocity profiles and the mass

flow rate. Apply the logarithmic profile of

Eq.

5.3-3 for the flow in the neighborhood of each

wall. Assume that the location of the maximum in the velocity occurs on the same cylindrical

surface

found for laminar annular flow:

H. Schlichting,

Boundary-Layer

Theoy,

McGraw-Hill, New

York,

4th edition (1960),

607 and

Fig.

23.7.

Problems

175

Measured velocity profiles suggest that this assumption for

is reasonable, at least for high

Reynolds numbem3 Assume further that

Eq.

5.3-3

is the same for the inner and outer

walls.

(a)

Show that direct application of

Eq.

5.3-3

leads immediately to the following velocity pro-

files4 in the region

bR (designated by

and

(designated by

>):

-->

r)v:

?=;ln(

)+A'

where

v,,m

in which

v.+

d(9,

9,)R/2Lp.

(b)

Obtain a relation between the constants

and

by requiring that the velocity be con-

tinuous at

bR.

(c)

Use the results of (b) to show that the mass flow rate through the annulus is

in which

5C.3 Instability

simple mechanical system

(Fig. 5C.3).

(a)

disk is rotating with a constant angular velocity

Above the center of the disk a

sphere of mass

is suspended by

massless rod of length

Because of the rotation of the

disk, the sphere experiences a centrifugal force and the rod makes an angle

with the verti-

cal. By making a force balance on the sphere, show that

cos

ln2L

What happens when

goes to zero?

sphere

Fig.

5C.3.

simple mechanical system for illustrating concepts

Knudsen and

Katz,

Fluid Dynamics and Heat Transfer,

McGraw-Hill, New York (1958);

Rothfus (1948),

Walker (19571, and

Whan (19561, Doctoral theses, Carnegie Institute of

Technology (now Carnegie-Mellon University), Pittsburgh,

Pa.

W. Tiedt,

Berechnung des laminaren u. turbulenten Reibungswiderstandes konzentrischer u. exzentrischer

Ringspalten,

Technischer Bericht Nr. 4, Inst.

Hydraulik u. Hydraulogie, Technische Hochschule,

Darmstadt (1968); D.

Meter and

B. Bird,

AIChE Journal,

7,4145 (1961) did the same analysis using

the Prandtl mixing length theory.

176

Chapter 5 Velocity Distributions in Turbulent Flow

(b)

Show that, if

is below some threshold value a,,,, the angle 8 is zero. Above the thresh-

old value, show that there are two admissible values for 8. Explain by means of a carefully

drawn sketch of

vs. fl. Above

a,,,

label the two curves

stable

and

unstable.

(c)

In (a) and (b) we considered only the steady-state operation of the system. Next show that

the equation of motion for the sphere of mass

d28

rnf12~

sin 8 cos

sin

df2

(5C.3-2)

Show that for steady-state operation this leads to Eq. 5C.3-1. We now want to use this

equation to make a small-amplitude stability analysis. Let 0

O,, where

is a steady-

state solution (independent of time) and 8, is a very small perturbation (dependent on

time).

(d) Consider first the lower branch in (b), which is 0,

Then sin 1'3

sin 8,

and cos 6

cos 8,

so that Eq. 5B.2-2 becomes

We now try a small-amplitude oscillation of the form 8,

A9?{e-'"tJ

and find that

Now consider two cases: (i) If

f12

g/L, both

and

are real, and hence

oscillates; this

indicates that for

f12

g/L the system is stable. (ii) If

f12

g/L, the root

is positive imagi-

nary and

e-'"'

will increase indefinitely with time; this indicates that for f12

g/L

the system

is unstable with respect to infinitesimal perturbations.

(e) Next consider the upper branch in (b). Do an analysis similar to that in (d). Set up the

equation for 8, and drop terms in the square of 0, (that is, linearize the equation). Once again

try a solution of the form 8,

A%{e-'"il.

Show that for the upper branch the system is stable

with respect to infinitesimal perturbations.

(f)

Relate the above analysis, which is for a system with one degree of freedom, to the prob-

lem of laminar-turbulent transition for the flow of a Newtonian fluid in the flow between two

counter-rotating cylinders. Read the discussion by Landau and ~ifshitz~ on this point.

5D.1 Derivation of the equation of change for the Reynolds stresses. At the end of 55.2 it was

pointed out that there is an equation of change for the Reynolds stresses. This can be derived

by (a) multiplying the ith component of the vector form of Eq. 5.2-5 by

and time smoothing,

(b)

multiplying the jth component of the vector form of Eq. 5.2-5 by

and time smoothing, and

(c)

adding the results of (a) and

(b).

Show that one finally gets

Equations 5.2-10 and

will be needed in this development.

5D.2 Kinetic energy of turbulence. By taking the trace of Eq. 5D.1-1 obtain the following:

Interpret the eq~ation.~

Landau and

Lifshitz,

Fluid Mechanics,

Pergamon,

Oxford,

2nd edition

(1987),

§§26-27.

Tennekes and

Lumley,

First Course

Turbulence,

MIT Press, Cambridge, Mass.

(1972),§3.2.