Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

1.2

Special Forms of the Energy Equation

337

put in the substantial derivative form by using Eq. 3.5-4. This gives, with no further

assumptions

Next it is convenient to switch from intynalnenergy to ythalpy, as we did at the very

end of

59.8.

That is, in Eq. 11.2-2 we set

(p/p), making the standard

assumption that thermodynamic formulas derived from equilibrium thermodynamics

may be applied locally for nonequilibrium systems. When we substitute this formula

into Eq. 11.2-2 and use the equation of continuity (Eq.

of Table 3.5-I), we get

Next we may use Eq. 9.8-7, which presumes that the enthalpy is a function of

and T

(this restricts the subsequent development to Newtonian fluids). Then we may get an ex-

pression for the change

the enthalpy in an element of fluid moving with the fluid ve-

locity, which is

Equating the right sides of Eqs. 11.2-3 and 11.2-4 gives

This is the equation

change for temperature, in terms of the heat flux vector q and the

viscous momentum flux tensor

To use this equation we need expressions for these

fluxes:

(i)

When Fourier's law of Eq. 9.1-4 is used, the term

-(V

q) becomes +(V

kVT),

or, if the thermal conductivity is assumed constant, +kV2T.

(ii)

When Newton's law of Eq. 1.2-7 is used, the term -(T:VV) becomes

pa,

KIP,,

the quantity given explicitly in Eq. 3.3-3.

We do not perform the substitutions here, because the equation of change for tempera-

ture is almost never used in its complete generality.

We now discuss several special restricted versions of the equation of change for tem-

perature.

all of these we use Fourier's law with constant

and we omit the viscous

dissipation term, since it is important only in flows with enormous velocity gradients:

(i)

For an ideal

gas,

In p/d In

T),

-1, and

Or, if use is made of the relation

the equation of state in the form

pXT, and the equation of continuity as written in Eq.

of Table 3.5-1, we get

338

Chapter 11 The Equations of Change for Nonisothermal Systems

(ii) For a fluid flowing in a constant pressure system, Dp/Dt

0, and

(iii) For a fluid with constant density,' (d In p/d In

and

(iv) For a stationa

solid, v is zero and

dl-

kV2T

(1 1.2-10)

These last five equations are the ones most frequently encountered in textbooks and re-

search publications. Of course, one can always go back to Eq. 11.2-5 and develop less

re-

strictive equations when needed. Also, one can add chemical, electrical, and nuclear

source terms on an ad hoc basis, as was done in Chapter 10.

Equation 11.2-10 is the heat conduction equation for solids, and much has been writ-

ten about this famous equation developed first by ~ourier.~ The famous reference work

by Carslaw and Jaeger deserves special mention. It contains hundreds of solutions of this

equation for a wide variety of boundary and initial conditions."

g11.3

THE BOUSSINESQ EQUATION OF MOTION

FOR FORCED

AND

FREE CONVECTION

The equation of motion given in Eq. 3.2-9 (or Eq.

of Table 3.5-1) is valid for both

isothermal and nonisothermal flow. In nonisothermal flow, the fluid density and viscos-

ity depend in general on temperature as well as on pressure. The variation in the density

is particularly important because it gives rise to buoyant forces, and thus to free convec-

tion, as we have already seen in s10.9.

The buoyant force appears automatically when an equation of state is inserted into

the equation of motion. For example, we can use the simplified equation of state intro-

duced in Eq. 10.9-6 (this is called the Boussinesq approximation)'

in which

is -(l/p)(~p/dTIP evaluated at

This equation is obtained by writing

the Taylor series for p as a function of

considering the pressure

to be constant, and

keeping only the first two terms of the series. When Eq. 11.3-1 is substituted into the

term (but not into the p(Dv/Dt) term) of Eq.

of Table 3.5-1, we get the Boussinesq equation:

The assumption of constant density is made here, instead of the less stringent assumption that

In p/d In

T),

since Eq. 11.2-9 is customarily used along with Eq. 3.1-5 (equation of continuity

for

constant density) and Eq. 3.5-6 (equation of motion for constant density and viscosity). Note that the

hypothetical equation of state

constant has to be supplemented by the statement that (dp/dT),

finite, in order to permit the evaluation of certain thermodynamic derivatives. For example, the relation

leads to the result that

for the "incompressible fluid thus defined.

Fourier,

T'hkdie analytique de la chalhr, CEuvres de Fourier,

Gauthier-Villars et Fils, Paris (1822).

Carslaw and

Jaeger,

Conduction

Heat

Solids,

Oxford University Press, 2nd edition (1959).

Boussinesq,

Thkorie Analytique de Chaleur,

Vol. 2, Gauthier-Villars, Paris

(1903).

1.4

Use

of the Equations of

Change

to Solve Steady-State Problems

339

This form of the equation of motion is very useful for heat transfer analyses. It describes

the limiting cases of forced convection and free convection (see Fig. 10.8-I), and the re-

gion between these extremes as well. In forced convection the buoyancy term

-@&T

is neglected. In

free

convection (or natural convection) the term (-Vp

pg) is small, and

omitting it is usually appropriate, particularly for vertical, rectilinear flow and for the

flow near submerged objects in large bodies of fluid. Setting

(-Vp

pg) equal to zero is

equivalent to assuming that the pressure distribution is just that for a fluid at rest.

It is also customary to replace p on the left side of Eq. 11.3-2 by

This substitution has

been successful for free convection at moderate temperature differences. Under these con-

ditions the fluid motion is slow, and the acceleration term Dv/Dt is small compared to

However, in systems where the acceleration term is large with respect to g, one must

also use

Eq.

11.3-1 for the density on the left side of the equation of motion. This is par-

ticularly true, for example, in gas turbines and near hypersonic missiles, where the term

p)Dv/Dt may be at least as important as pg.

$11.4

USE

THE

EQUATIONS OF CHANGE

SOLVE STEADY-STATE PROBLEMS

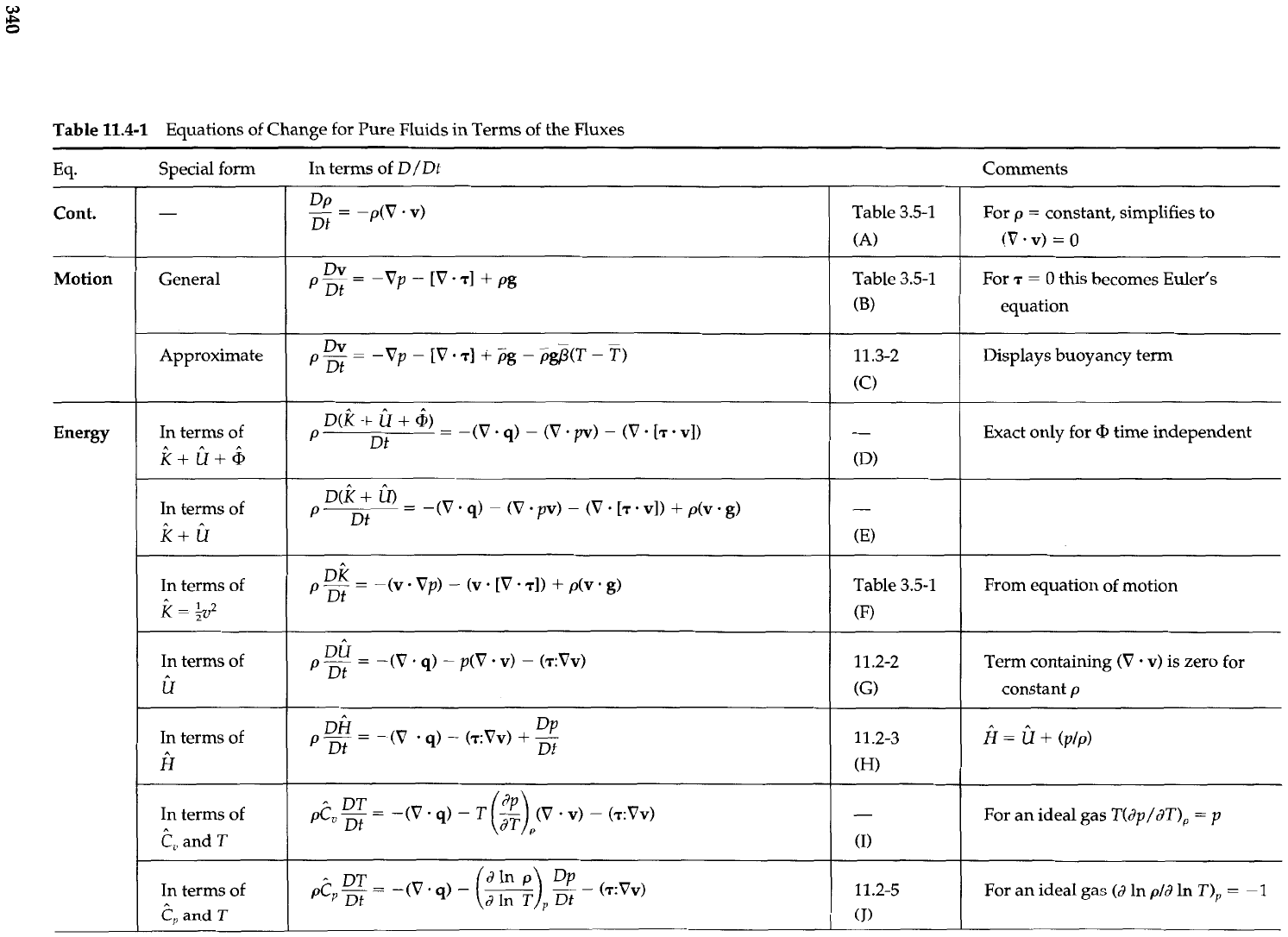
In 593.1 to 3.4 and in 591 1.1 to 11.3 we have derived various equations of change for a

pure fluid or solid. It seems appropriate here to present a summary of these equations

for future reference. Such a summary is given in Table 11.4-1, with most of the equations

given in both the

d/dt

form and the D/Dt form. Reference is also made to the first place

where each equation has been presented.

Although Table 11.4-1 is a useful summary, for problem solving we use the equa-

tions written out explicitly in the several commonly used coordinate systems. This has

been done in Appendix

and readers should thoroughly familiarize themselves with

the tables there.

In general, to describe the nonisothermal flow of a Newtonian fluid one needs

the equation of continuity

the equation of motion (containing

and

the equation of energy (containing

and

the thermal equation of state

p(p,

TI)

the caloric equation of state

k&p,

T))

as well as expressions for the density and temperature dependence of the viscosity, di-

latational viscosity, and thermal conductivity. In addition one needs the boundary and

initial conditions. The entire set of equations can then-in principle-be solved to get the

pressure, density, velocity, and temperature as functions of position and time. If one

wishes to solve such a detailed problem, numerical methods generally have to be used.

Often one may be content with a restricted solution, for making an order-of-magni-

tude analysis of a problem, or for investigating limiting cases prior to doing a complete

numerical solution. This is done by making some standard assumptions:

(i)

Assumption of constant physical properties. If it can be assumed that all physical

properties are constant, then the equations become considerably simpler, and

in some cases analytical solutions can be found.

(ii)

Assumption of zero fluxes. Setting

and

equal to zero may be useful for (a) adi-

abatic flow processes in systems designed to minimize frictional effects (such as

Venturi meters and turbines), and (b) high-speed flows around streamlined ob-

jects. The solutions obtained would be of no use for describing the situation

near fluid-solid boundaries, but may be adequate for analysis of phenomena

far from the solid boundaries.

Table

11.4-1

Equations of Change for Pure Fluids in Terms of the Fluxes

Special form

In terms of

D/Dt

Comments

Table

3.5-1

(A)

For

constant, simplifies to

(V.v)

Cont.

For

this becomes Euler's

equation

Displays buoyancy term

Motion

General

Table

3.5-1

(B)

Approximate

Exact only for

time independent

Energy

In terms of

k+ir+6

In terms of

K+U

DIZ

---

-(v

Vp)

.TI)

p(v.

From equation of motion Table

3.5-1

(F)

terms of

I;:

fv2

Term containing

zero for

constant

(PIP)

In terms of

e,,

and

For an ideal gas T(dp/dT),

For an ideal

gas

(6'

pld

T),

In terms of

and

Cont.

Motion

Energy

Entropy

General

In terms of

ap(~

C+ 6)

-v~+

(v-q)

(V.[T.V])

I;l+u+$J

In terms of

dp(k+ ir)

(v-[T.v)I +p(vag)

i+u

In terms of

1;:

iV2

terms of

In terms of

For

constant, simplifies to

For

this becomes Euler's

equation

Displays buoyancy term

Exact only for

time independent

Exact only for time independent

From equation of motion

Term containing

(V v)

is zero for

constant

Last two terms describe entropy

production

342

Chapter

The Equations of Change for Nonisothermal Systems

EXAMPLE

11.4-1

Steady-State Forced-

Convection Heat

Transfer in Laminar

Flow

in a Circular Tube

EXAMPLE

11.4-2

Tangential Flow in an

Annulus with Viscous

Heat Generation

To illustrate the solution of problems in which the energy equation plays a signifi-

cant role, we solve a series of (idealized) problems. We restrict ourselves here to steady-

state flow problems and consider unsteady-state problems in Chapter

12.

In each

problem we start by listing the postulates that lead us to simplified versions of the equa-

tions of change.

Show how to set up the equations for the problem considered in 510.8-namely, that of find-

ing the fluid temperature profiles for the fully developed laminar flow in a tube.

SOLUTION

We assume constant physical properties, and we postulate a solution of the following form:

6,v,(r),

Wz), and

T(r, z). Then the equations of change, as given in Appendix

may be simplified to

Continuity: 0

0 (11.4-1)

Motion:

Energy:

The equation of continuity is automatically satisfied as a result of the postulates. The equation

of motion, when solved as in Example 3.6-1, gives the velocity distribution (the parabolic ve-

locity profile). This expression is then substituted into the convective heat transport term on

the left side of Eq.

11.4-3

and into the viscous dissipation heating term on the right side.

Next, as in 510.8, we make two assumptions: (i) in the

direction, heat conduction

much smaller than heat convection, so that the term d2T/dz2 can be neglected, and (ii) the

flow is not sufficiently fast that viscous heating is significant, and hence the term p(dv,/dr)2

can be omitted. When these assumptions are made, Eq.

11.4-3

becomes the same as

Eq.

10.8-

12.

From that point on, the asymptotic solution, valid for large

only, proceeds as in s10.8.

Note that we have gone through three types of restrictive processes: (i) postulates, in which

a tentative guess is made as to the form of the solution; (ii) assumptions, in which we elimi-

nate some physical phenomena or effects by discarding terms or assuming physical proper-

ties to be constant; and (iii) an asymptotic solution, in which we obtain only a portion of the

entire mathematical solution. It is important to distinguish among these various kinds of

restrictions.

Determine the temperature distribution in an incompressible liquid confined between two

coaxial cylinders, the outer one of which is rotating at a steady angular velocity

(see 510.4

and Example 3.6-3). Use the nomenclature of Example 3.6-3, and consider the radius ratio

be fairly small so that the curvature of the fluid streamlines must be taken into account.

The temperatures of the inner and outer surfaces of the annular region are maintained

and

TI,

respectively, with

T,.

Assume steady laminar flow, and neglect the tempera-

ture dependence of the physical properties.

This is an example of a forced convection problem: The equations of continuity and mo-

tion are solved to get the velocity distribution, and then the energy equation is solved to get

the temperature distribution. This problem is of interest in connection with heat effects in

coaxial cylinder viscometers' and in lubrication systems.

Van

Wazer,

Lyons,

Kim,

and

Colwell,

Viscosity

and

Flow

Measurement,

Wiley,

New

York

(1963),

pp.

82-85.

g11.4

Use of the Equations of Change to Solve Steady-State Problems

343

SOLUTION

We begin by postulating that

Zi,v,(r), that

9(r,

z),

and that

T(r). Then the simplifi-

cation of the equations of change leads to Eqs. 3.6-20,21, and

(the r-,

8-,

and z-components

of the equation of motion), and the energy equation

When the solution to the 0-component of the equation of motion, given in Eq. 3.6-29, is substi-

tuted into the energy equation, we get

This is the differential equation for the temperature distribution. It may be rewritten in terms

of dimensionless quantities

putting

The parameter

is closely related to the Brinkman number of 910.4. Equation 11.4-5 now

becomes

This is of the form of Eq. C.l-11 and has the solution

The integration constants are found from the boundary conditions

B.C.

Determination of the constants then leads to

When

0, we obtain the temperature distribution for a motionless cylindrical shell of

thickness R(1

with inner and outer temperatures

and TI. If

is large enough, there

will be a maximum in the temperature distribution, located at

with the temperature at this point greater than either T, or TI.

Although this example provides an illustration of the use of the tabulated equations of

change in cylindrical coordinates, in most viscometric and lubrication applications the clear-

ance between the cylinders is so small that numerical values computed from Eq. 11.4-13 will

not differ substantially from those computed from Eq. 10.4-9.

EXAMPLE

11.4-3

liquid is flowing downward in steady laminar flow along an inclined plane surface, as

shown in Figs. 2.2-1 to

The free liquid surface is maintained at temperature To, and the solid

Steady

Flow

surface at

is maintained at

T,.

At these temperatures the liquid viscosity has values

Nonisothermal

Film

and

pb,

respectively, and the liquid density and thermal conductivity may be assumed con-

stant. Find the velocity distribution in this nonisothermal flow system, neglecting end effects

344

Chapter 11 The Equations of Change for Nonisothermal Systems

and recognizing that viscous heating is unimportant in this flow. Assume that the tempera-

ture dependence of viscosity may be expressed by an equation of the form

AeBIT, with

and

being empirical constants; this is suggested by the Eyring theory given in 51.5.

We first solve the energy equation to get the temperature profile, and then use the latter

to find the dependence of viscosity on position. Then the equation of motion can be solved

get the velocity profile.

SOLUTION

We postulate that T

T(x) and that

6,vJx).

Then the energy equation simplifies to

This can be integrated between the known terminal temperatures to give

The dependence of viscosity on temperature may be written as

in which

is a constant, to be determined from experimental data for viscosity versus tem-

perature. To get the dependence of viscosity on position, we combine the last two equations

to get

The second expression is a good approximation if the temperature does not change greatly

through the film. When this equation is combined with Eq. 11.4-17, written for T

T,,

then get

This is the same as the expression used in Example 2.2-2, if we set

equal to -ln(p,/p,).

Therefore we may take over the result from Example 2.2-2 and write the velocity profile as

This completes the analysis of the problem begun

Example 2.2-2, by providing the appro-

priate value of the constant

EXAMPLE

11.4-4

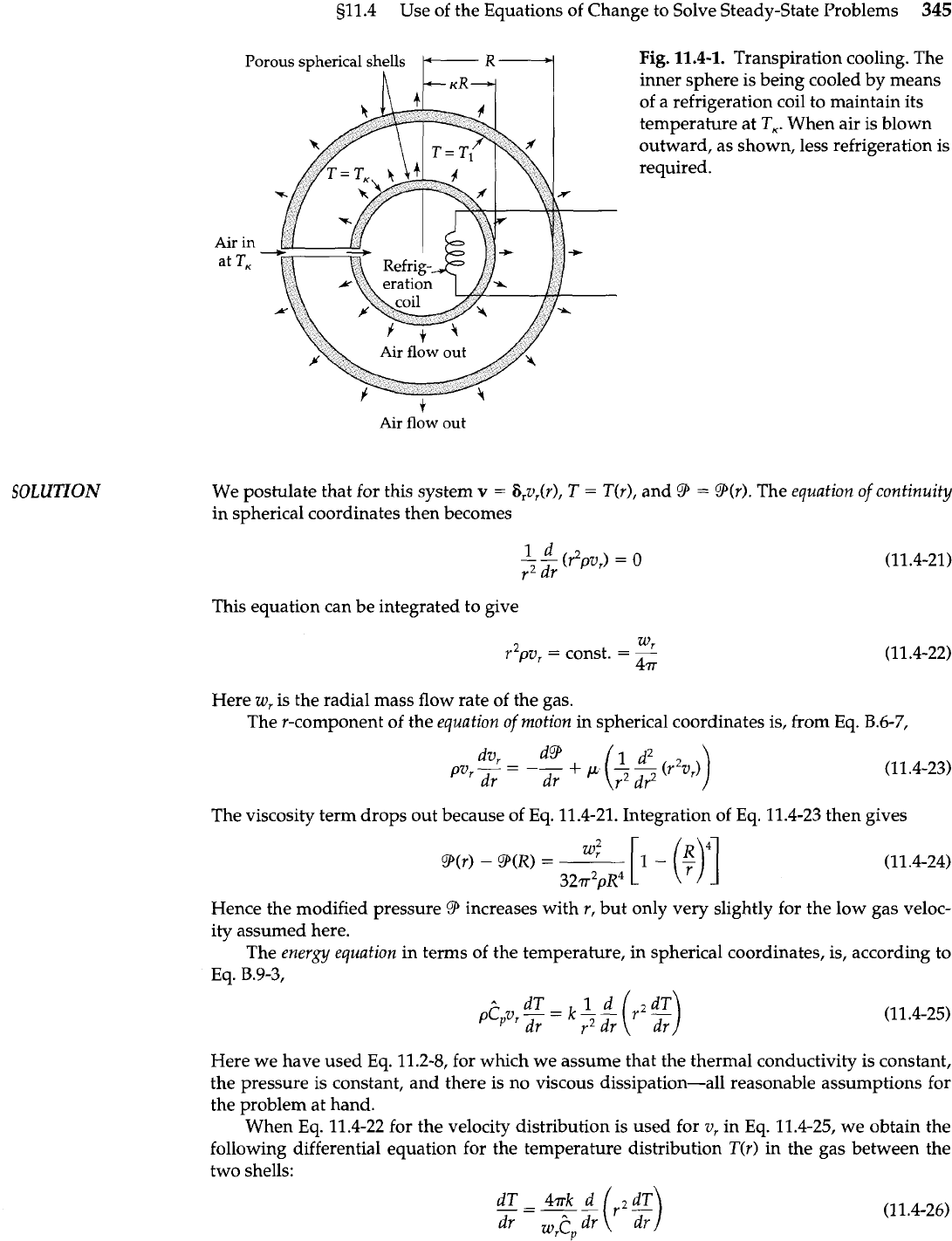
Transpiration cooling2

A system with two concentric porous spherical shells of radii

and

is shown in Fig. 11.4-

1. The inner surface of the outer shell is at temperature T,, and the outer surface of the inner

shell is at a lower temperature TK. Dry air at TK is blown outward radially from the inner shell

into the intervening space and then through the outer shell. Develop an expression for the re-

quired rate of heat removal from the inner sphere as a function of the mass rate of flow of the

gas. Assume steady laminar flow and low gas velocity.

In this example the equations of continuity and energy are solved to get the temperature

distribution. The equation of motion gives information about the pressure distribution in

the

system.

Jakob,

Heat Transfer,

Vol.

Wiley,

New

York

(1957),

pp.

394-415.

g11.4 Use of the Equations of Change to Solve Steady-State Problems

345

SOLUTION

Porous

spherical shells

L-I

Air

flow

out

Fig.

11.4-1.

Transpiration cooling. The

inner sphere is being cooled by means

of a refrigeration coil to maintain its

temperature at

TK.

When air is blown

outward, as shown, less refrigeration is

required.

We postulate that for this system

6pr(r),

T(r), and

Wr). The

equation of continuity

in spherical coordinates then becomes

This equation can be integrated to give

pv,

const.

4Tr

Here

is the radial mass flow rate of the gas.

The r-component of the

equation of mofion

in spherical coordinates is, from Eq.

B.6-7,

The viscosity term drops out because of Eq. 11.4-21. Integration of Eq. 11.4-23 then gives

Hence the modified pressure

increases with r, but only very slightly for the low gas veloc-

ity assumed here.

The

energy equation

in terms of the temperature, in spherical coordinates, is, according to

Eq.

B.9-3,

Here we have used Eq. 11.2-8, for which we assume that the thermal conductivity is constant,

the pressure is constant, and there is no viscous dissipation-all reasonable assumptions for

the problem at hand.

When Eq. 11.4-22 for the velocity distribution is used for

in Eq. 11.4-25, we obtain the

following differential equation for the temperature distribution T(r) in the gas between the

two shells:

346

Chapter 11 The Equations of Change for Nonisothermal Systems

1.0

Fig.

11.4-2.

The effect of transpira-

tion cooling.

0.8

.r(

0.6

a'01

0.4

0.2

Dimensionless transpiration rate,

We make the change of variable

r2(dT/dr) and obtain a first-order, separable differential

equation for

uW.

This may be integrated, and when the boundary conditions are applied,

get

in which Ro

w,Cp/4?~k is a constant with units of length.

The rate of heat flow toward the inner sphere is

and this is the required rate of heat removal by the refrigerant. Insertion of Fourier's law

for

the r-component of the heat flux gives

evaluate the temperature gradient at the surface with the aid of Eq. 11.4-27 to obtain

the expression for the heat removal rate.

In the limit that the mass flow rate of the gas is zero, so that R,

the heat removal rate

becomes

The fractional reduction in heat removal as

result of the transpiration of the gas is then

Here

Ro(l

K)/KR

w,Cp(l

K)/~TKR~ is the "dimensionless transpiration rate."

Equation 11.4-32 is shown graphically in Fig.

11.4-2.

For small values of

the quantity

(Qo

Q)/Qo approaches the asymptote

$4.

EXAMPLE

11.4-5

Free-Convection Heat

flat plate of height Hand width

(with

heated to a temperature To is suspended

in a large body of fluid, which is at ambient temperature

TI.

In the neighborhood of the

heated plate the fluid rises because of the buoyant force (see Fig. 11.4-3). From the equations

Transfer from

of change, deduce the dependence of the heat loss on the system variables. The physical prop-

Vertical Plate

erties of the fluid are considered constant, except that the change in density with temperature

will be accounted for by the Boussinesq approximation.