Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

511.5

Dimensional Analysis of the Equations of Change for Nonisothermal Systems

357

(b)

Small

system (System

11):

(~.JII

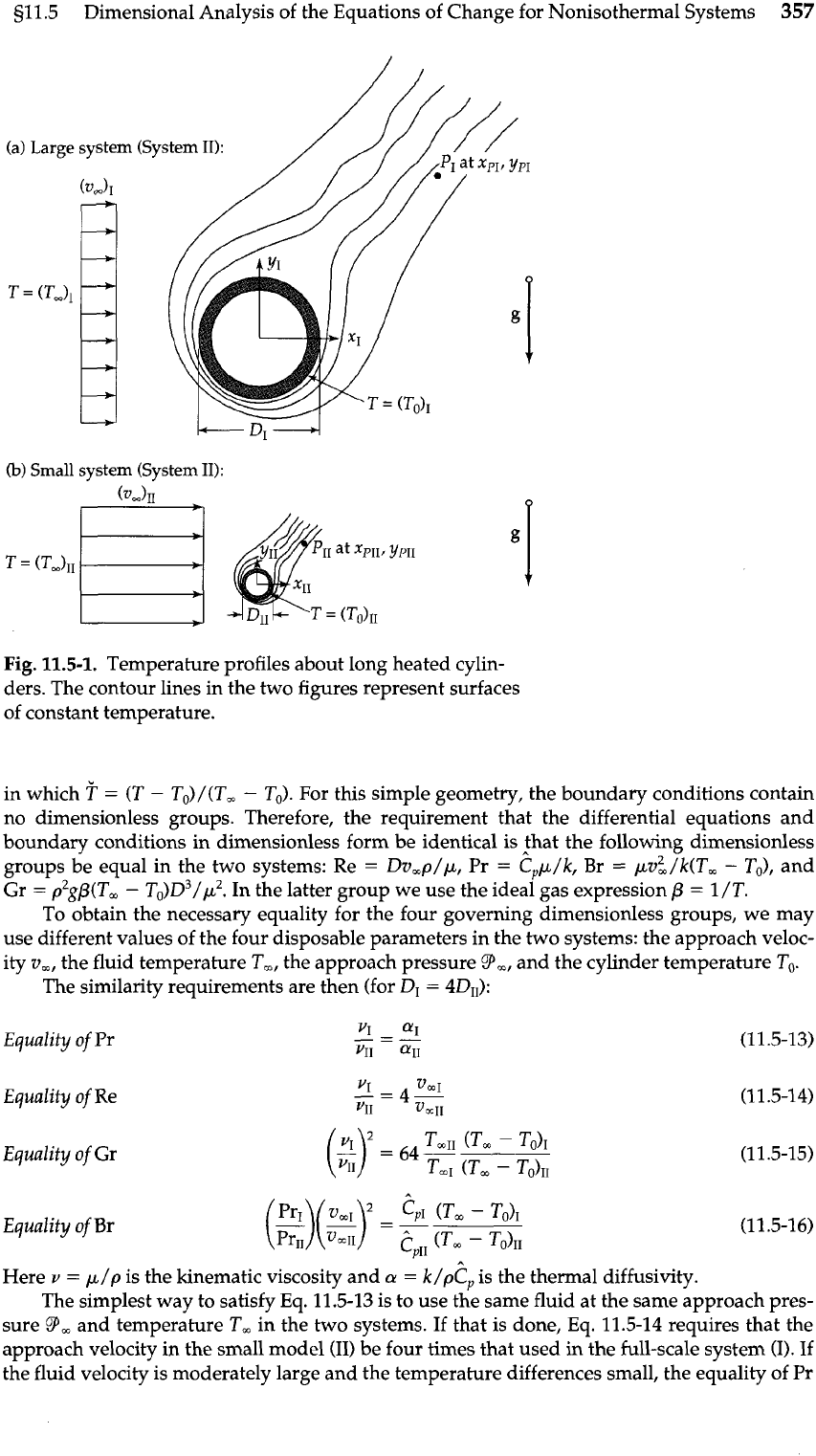
Fig.

11.5-1.

Temperature profiles about long heated cylin-

ders. The contour lines in the two figures represent surfaces

of constant temperature.

in which

To)/(T,

To). For this simple geometry, the boundary conditions contain

no dimensionless groups. Therefore, the requirement that the differential equations and

boundary conditions in dimensionless form be identical is _that the following dimensionless

groups be equal in the two systems: Re

Dv,p/p, Pr

C,p/k,

pv;/k(T,

To), and

p2g/3(T,

T,)D~/~~.

In the latter group we use the ideal gas expression

1/T.

To obtain the necessary equality for the four governing dimensionless groups, we may

use different values of the four disposable parameters in the two systems: the approach veloc-

ity v,, the fluid temperature

T,,

the approach pressure P,, and the cylinder temperature To.

The similarity requirements are then (for D1

4D11):

Equality

T-11 (T,

To11

(2)

(T,

To),,

Here

p/p is the kinematic viscosity and

k/pC, is the thermal diffusivity.

The simplest way to satisfy Eq. 11.5-13 is to use the same fluid at the same approach pres-

sure

and temperature

in the two systems. If that is done, Eq. 11.5-14 requires that the

approach velocity in the small model (11) be four times that used in the full-scale system

(I).

the fluid velocity is moderately large and the temperature differences small, the equality of Pr

358

Chapter 11 The Equations of Change for Nonisothermal Systems

and Re in the two systems provides a sufficient approximation to dynamic similarity. This is

the limiting case of forced convection with negligible viscous dissipation.

If, however, the temperature differences

are large, free-convection effects may be

appreciable. Under these conditions, according to Eq. 11.5-15, temperature differences

the

model must be 64 times those in the large system to ensure similarity.

From

Eq.

11.5-16 it may be seen that such a ratio of temperature differences will not per-

mit equality of the Brinkman number. For the latter a ratio of 16 would be needed. This

con-

flict will not normally arise, however, as free-convection and viscous heating effects are

seldom important simultaneously. Free-convection effects arise in low-velocity systems,

whereas viscous heating occurs to a significant degree only when velocity gradients are very

large.

EXAMPLE

11.5-2

Free Convection in a

Horizontal Fluid Layer;

We wish to investigate the free-convection motion in the system shown in Fig. 11.5-2. It con-

sists of a thin layer of fluid between two horizontal parallel plates, the lower one at tempera-

ture

T,,

and the upper one at

T,,

with

To.

In the absence of fluid motion, the conductive

heat flux will be the same for all z, and a nearly uniform temperature gradient will be estab-

Formation of &kard

lished at steady state. This temperature gradient will in turn cause a density gradient. If the

density decreases with increasing z, the system will clearly be stable, but

it increases a

po-

tentially unstable situation occurs. It appears possible in this latter case that any chance dis-

turbance may cause the more dense fluid to move downward and displace the lighter fluid

beneath it. If the temperatures of the top and bottom surfaces are maintained constant, the

re-

sult may be a continuing free-convection motion. This motion will, however, be opposed

viscous forces and may, therefore, occur only if the temperature difference tending to cause

is greater than some critical minimum value.

Determine by means of dimensional analysis the functional dependence of this fluid

mo-

tion and the conditions under which it may be expected to arise.

SOLUTION

The system is described by Eqs. 11.5-1 to

along with the following boundary conditions:

B.C. 1:

B.C.

Top

view

Side view

Fig.

11.5-2.

Bknard cells

formed in the region between

two horizontal parallel plates,

with the bottom plate at a

higher temperature than the

upper one. If the Rayleigh

number exceeds a certain

critical value, the system

becomes unstable and

hexagonal Bknard cells

are produced.

s11.5

Dimensional Analysis of the Equations of Change for Nonisothermal Systems

359

We now restate the problem in dimensionless form, using lo

h. We use the dimensionless

quantities listed under Case

in Table 11.5-1, and we select the reference temperature

to be

,(To

TI),

so that

Continuity:

ir)

1.5-20)

Motion:

Energy:

with dimensionless boundary conditions

B.C. 1:

B.C.

If the above dimensionless equations could be solved along with the dimensionless boundary

conditions, we would find that the velocity and temperature profiles would depend only on

Gr, Pr, and R/h. Furthermore, the larger the ratio R/h is, the less prominent its effect will be,

and in the limit of extremely large horizontal plates, the system behavior will depend solely

on Gr and Pr.

If we consider only steady creeping flows, then the term Dt/D; may be set equal to zero.

Then we define a new dimensionless pressure difference as

~r8. With the left side of Eq.

11.5-21 equal to zero, we may now divide by Pr and the resulting equation contains oniy one

dimensionless group, namely the Rayleigh number' Ra

GrPr

p2gp(~,

~,)h~c?/~k,

whose value will determine the behavior of the system. This illustrates how one may reduce

the number of dimensionless groups that are needed to describe a nonisothermal flow system.

The preceding analysis suggests that there may be a critical value of the Rayleigh num-

ber, and when this critical value is exceeded, fluid motion will occur. This suggestion has

been amply confirmed e~perimentall~~,~ and the critical Rayleigh number has been found to

be 1700

51 for R/h>>l. For Rayleigh numbers below the critical value, the fluid is station-

ary, as evidenced by the observation that the heat flux across the liquid layer is the same as

that predicted for conduction through a static fluid:

k(To

TJ/h. As soon as the critical

Rayleigh number is exceeded, however, the heat flux rises sharply, because of convective en-

ergy transport. An increase of the thermal conductivity reduces the Rayleigh number, thus

moving Ra toward its stable range.

The assumption of creeping flow is a reasonable one for this system and is asymptoti-

cally correct when Pr

c-~.

It is also very convenient, inasmuch as it allows analytic solutions

of the relevant equations of ~hange.~ One such solution, which agrees well with experiment,

is sketched qualitatively in Fig. 11.5-2. This flow pattern is cellular and hexagonal, with up-

flow at the center of each hexagon and downflow at the periphery. The units of this fascinat-

ing pattern are called Bknard

cells.5

The analytic solution also confirms the existence of a

critical Rayleigh number. For the boundary conditions of this problem and very large R/h it

has been calculated4 to be 1708, which is in excellent agreement with the experimental result

cited above.

The Rayleigh number is named after Lord Rayleigh

Strutt),

Phil. Mag.,

(6) 32,529-546 (1916).

Silveston,

Forsch. Ingenieur-Wesen,

24,2932,5949 (1958).

Chandrasekhar,

Hydrodynamic and Hydromagnetic Instability,

Oxford University Press

(1961);

Faber,

Fluid Dynamics for Physicists,

Cambridge University Press

(1995), 58.7.

Pellew and

Southwell,

Proc. Roy. Soc.,

A176,312-343 (1940).

Benard,

Revue gt!nt!rale des sciences pures et appliquies,

11,1261-1271,1309-1328 (1900);

Annales de

Chimie et de Physique,

23,62-144 (1901).

360

Chapter 11 The Equations of Change for Nonisothermal Systems

Similar behavior is observed for other boundary conditions. If the upper plate of Fig.

11.5-2 is replaced by a liquid-gas interface, so that the surface shear stress in the liquid is neg-

ligible, cellular convection is predicted theoretically3 for Rayleigh numbers above about 1101.

A spectacular example of this type of instability occurs in the occasional spring "turnover"

water in northern lakes. If the lake water is cooled to near freezing during the winter, an ad-

verse density gradient will occur as the surface waters warm toward

4"C,

the temperature

maximum density for water.

In shallow liquid layers with free surfaces, instabilities can also arise from surface-ten-

sion gradients. The resulting surface stresses produce cellular convection superficially similar

to that resulting from temperature gradients, and the two effects may be easily confused. In-

deed, it appears that the steady flows first seen by Bhard, and ascribed to buoyancy effects,

may actually have been produced by surface-tension

gradient^.^

EXAMPLE 11.5-3

Surface Temperature

An electrical heating coil of diameter

is being designed to keep a large tank of liquid above

its freezing point. It is desired to predict the temperature that will be reached at the coil sur-

face as a function of the heating rate

and the tank surface temperature

To.

This prediction is

an Electrical Heating

to be made on the basis of experiments with a smaller, geometrically similar apparatus filled

Coil

with the same liquid.

Outline a suitable experimental procedure for making the desired prediction. Tempera-

ture dependence of the physical properties, other than the density, may be neglected. The en-

tire heating coil surface may be assumed to be at a uniform temperature

T,.

SOLUTION

This is a free-convection problem, and we use the column labeled A in Table 11.5-1 for the di-

mensionless groups. From the equations of change and the boundary conditions, we know

that the dimensionless temperature

To)/(T,

To)

must be a function of the dimen-

sionless coordinates and depend on the dimensionless groups Pr and Gr.

The total energy input rate through the coil surface is

Here

is the coordinate measured outward from and normal to the coil surface,

is the sur-

face area of the coil, and the temperature gradient is that of the fluid immediately adjacent to

the coil surface. In dimensionless form this relation is

in which

is a function of Pr

kPp/k

and Gr

p2gp(T,

~,)~~//lr

Since the large-scale and

small-scale systems are geometrically similar, the dimensionless function

describing

the

surface of integration will be the same for both systems and hence does not need to be in-

cluded in the function

Similarly, if we write the boundary conditions for temperature, ve-

locity, and pressure at the coil and tank surfaces, we will obtain only size ratios that will

identical in the two systems.

We now note that the desired quantity

(TI

To)

appears on both sides of

Eq.

11.5-27.

we multiply both sides of the equation by the Grashof number, then

(T,

To)

appears only

on the right side:

Sternling

and

L. E.

Scriven,

MChE

journal,

5,514-523 (1959);

Scriven

and

Sternling,

j. Fluid

Mech.,

19,321-340 (1964).

Problems

361

In principle, we may solve Eq. 11.5-28 for Gr and obtain an expression for (TI

To).

Since we

are neglecting the temperature dependence of physical properties, we may consider the

Prandtl number constant for the given fluid and write

Here

is an experimentally determinable function of the group

~p'gp~~/k~~.

We may then

construct a plot of Eq. 11.5-29 from the experimental measurements of TI,

To,

and

for the

small-scale system, and the known physical properties of the fluid. This plot may then be

used to predict the behavior of the large-scale system.

Since we have neglected the temperature dependence of the fluid properties, we may go

even further. If we maintain the ratio of the

values in the two systems equal to the inverse

square of the ratio of the diameters, then the corresponding ratio of the values of

(TI

To)

will be equal to the inverse cube of the ratio of the diameters.

QUESTIONS FOR DISCUSSION

Define energy, potential energy, kinetic energy, and internal energy. What common units are

used for these?

How does one assign the physical meaning to the individual terms in Eqs. 11.1-7 and 11.2-I?

getting Eq. 11.2-7 we used the relation

which is valid for ideal gases. What is the

corresponding equation for nonideal gases and liquids?

Summarize all the steps required in obtaining the equation of change for the temperature.

Compare and contrast forced convection and free convection, with regard to methods of

problem solving, dimensional analysis, and occurrence in industrial and meteorological prob-

lems.

If a rocket nose cone were made of a porous material and a volatile liquid were forced slowly

through the pores during reentry into the atmosphere, how would the cone surface tempera-

ture be affected and why?

What is Archimedes' principle, and how is it related to the term

&$(T

in Eq. 11.3-2?

Would you expect to see Bknard cells while heating a shallow pan of water on a stove?

When, if ever, can the equation of energy be completely and exactly solved without detailed

knowledge of the velocity profiles of the system?

10.

When, if ever, can the equation of motion be completely solved for a nonisothermal system

without detailed knowledge of the temperature profiles of the system?

PROBLEMS

11A.1.

Temperature in a friction bearing.

Calculate the maximum temperature in the friction bear-

ing of Problem 3A.1, assuming the thermal conductivity of the lubricant to be

4.0

cal/s

C, the metal temperature 200°C, and the rate of rotation 4000 rpm.

Answer:

About 217°C (from both Eq. 11.4-13 and Eq. 10.4-9)

llA.2.

Viscosity variation and velocity gradients in a nonisothermal film.

Water is falling down a

vertical wall in a film

0.1

mm thick. The water temperature is 100°C at the free liquid surface

and 80°C at the wall surface.

(a)

Show that the maximum fractional deviation between viscosities predicted by Eqs. 11.4-17

and 18 occurs when T

(b)

Calculate the maximum fractional deviation for the conditions given.

Answer:

(b)

0.5%

362

Chapter 11 The Equations of Change for Nonisothermal Systems

Transpiration cooling.

(a) Calculate the temperature distribution between the two shells of Example 11.4-4 for radial

mass flow rates of zero and g/s for the following conditions:

500 microns

300°C

100 microns

100°C

6.13

cal/cm s

0.25 cal/g

(b) Compare the rates of heat conduction to the surface at

in the presence and absence of

convection.

Free-convection heat loss from a vertical surface.

small heating panel consists essentially

of a flat, vertical, rectangular surface 30 cm high and 50 cm wide. Estimate the total rate of

heat loss from one side of this panel by free convection, if the panel surface is at 150°F, and

the surrounding air is at 70°F and

atm. Use the value C

0.548 of Lorenz in

Eq.

11.4-51 and

the value of

recommended by Whitaker, and compare the results of the two calculations.

Answer:

8.1 cal/sec by Lorenz expression

Velocity, temperature, and pressure changes in a shock wave. Air at

atm and 70°F is

flow-

ing at an upstream Mach number of 2 across a stationg shock wave. Calculate the following

quantities, assuming that

is constant at 1.4 and that C,

0.24 Btu/lb,

(a) The initial velocity of the air.

(b) The velocity, temperature, and pressure downstream from the shock wave.

(c)

The changes of internal and kinetic energy across the shock wave.

Answer:

(a) 2250 ft/s

(b) 844 ft/s; 888

4.48 atm

(c)

f61.4 Btu/lb,;

86.9 Btu/lb,

Adiabatic frictionless compression of an ideal gas. Calculate the temperature attained

compressing air, initially at 100°F and

atm, to 0.1 of its initial volume. It is assumed that

1.40 and that the compression is frictionless and adiabatic. Discuss the result in relation to the

operation of an internal combustion engine.

Answer:

950°F

Effect of free convection on the insulating value of a horizontal air space. Two large parallel

horizontal metal plates are separated by a 2.5 cm air gap, with the air at an average temperature

of 100°C. How much hotter may the lower plate be (than the upper plate) without causing the

onset of the cellular free convection discussed in Example 11.5-2? How much may this tempera-

ture difference be increased if a very thin metal sheet is placed midway between the two plates?

Answers:

Approximately

and 48"C, respectively.

Adiabatic frictionless processes in an ideal gas.

(a) Note that a gas that obeys the ideal gas law may deviate appreciably from

constant.

Hence, rework Example 11.4-6 using a molar heat capacity expression of the form

(b) Determine the final pressure,

p,,

required if methane (CH,) is to be heated from 300K and

atm to 800K by adiabatic frictionless compression. The recommended empirical constants'

Hougen,

Watson, and

Ragatz,

Chemical Process Principles,

Part

2nd

edition,

Wiley,

New

York

(1958),

255.

See

also Part

11,

pp.

646-653,

for a fuller discussion of isentropic process calculations.

Problems

363

for methane are:

2.322 cal/g-mole

38.04

cal/g-mole K2, and

-10.97

lop6

cal/g-mole K3.

Answers:

(a)

exp[-(b/R)T

(c/2R)~~l

constant;

(b)

270 atm

llB.2. Viscous heating in laminar tube flow (asymptotic solutions).

(a)

Show that for fully developed laminar Newtonian flow in a circular tube of radius R, the

energy equation becomes

the viscous dissipation terms are not neglected. Here

v,,,,

is the maximum velocity in the

tube. What restrictions have to be placed on any solutions of Eq. 118.2-I?

(b)

For the

isothermal wall

problem

To at

for

0 and at

0 for all r), find the as-

ymptotic expression for

T(r)

at large

Do this by recognizing that

dT/dz

will be zero at large

Solve Eq. 118.2-1 and obtain

(c)

For the

adiabatic wall

problem

(9,

0 at r

for all

an asymptotic expression for large

may be found as follows: Multiply by

rdr

and then integrate from

Then inte-

grate the resulting equation over

to get

in which

is the inlet temperature at

0. Postulate now that an asymptotic temperature

profile at large

is of the form

Substitute this into

Eq.

llB.2-1 and integrate the resulting equation for

f(r)

to obtain

after determining the integration constant by an energy balance over the tube from 0 to

Keep in mind that Eqs. llB.2-2 and

are valid solutions only for large

The complete solu-

tions for small

are discussed in Problem llD.2.

11B.3.

Velocity distribution in a nonisothermal film.

Show that Eq. 11.4-20 meets the following

requirements:

(a)

(b)

av,/ax

llB.4. Heat conduction in a spherical shell

(Fig. llB.4).

spherical shell has inner and outer radii

and R,. A hole is made in the shell at the north pole by cutting out the conical segment in

the region 0

81.

A similar hole is made at the south pole by removing the portion

(.rr

8,)

The surface

is kept at temperature

TI,

and the surface at

held at T

T2. Find the steady-state temperature distribution, using the heat conduction

equation.

364

Chapter

The Equations of Change for Nonisothermal Systems

Solid

Hole at top

(at "north pole")

Fig.

llB.4.

Heat conduction in a spherical shell:

(a)

cross section

containing the z-axis;

(b)

view of the sphere from above.

118.5.

Axial heat conduction in

wire2 (Fig.

llB.5).

wire of constant density

moves downward

with uniform speed

into a liquid metal bath at temperature

T,.

It is desired to find the tem-

perature profile

T(z).

Assume that

at z

03,

and that resistance to radial heat conduc-

tion is negligible. Assume further that the wire temperature is

(a)

First solve the problem for constant physical properties

and

Obtain

(b)

Next solve the problqn when

and

are known functions of the dimensionless temper-

ature

k,K(@)

and

C,,L(@).

Obtain the temperature profile,

(c)

Verify that the solution in (b) satisfies the differential equation from which it was derived.

\~em~erature of wire far

from liquid metal

surface is

Wire moves downward

with constant speed

Liauid metal surface

at temperature

Fig.

llB.5.

Wire moving into a liquid metal bath.

Suggested

Prof.

Borman, Mechanical Engineering Department, University of Wisconsin.

Problems

365

118.6.

Transpiration cooling in a planar system. Two large flat porous horizontal plates are sepa-

rated by a relatively small distance

The upper plate at

is at temperature TL, and the

lower one at

is to be maintained at a lower temperature

To.

To reduce the amount of

heat that must be removed from the lower plate, an ideal gas at

is blown upward through

both plates at a steady rate. Develop an expression for the temperature distribution and the

amount of heat

that must be removed from the cold plate p_er unit area as a function of the

fluid properties and gas flow rate. Use the abbreviation

pC,v,L/k.

e4~lL

Answer:

-----

;qo=

llB.7.

Reduction of evaporation losses

transpiration (Fig.

llB.7).

It is proposed to reduce the

rate of evaporation of liquefied oxygen in small containers by taking advantage of transpira-

tion. To do this, the liquid is to be stored in a spherical container surrounded by a spherical

shell of a porous insulating material as shown in the figure. A thin space is to be left between

the container and insulation, and the opening in the insulation is to be stoppered. In opera-

tion, the evaporating oxygen is to leave the container proper, move through the gas space,

and then flow uniformly out through the porous insulation.

Calculate the rate of heat gain and evaporation loss from a tank

ft in diameter cov-

ered with a shell of insulation

in. thick under the following conditions with and without

transpiration.

Temperature of liquid oxygen

-297°F

Temperature of outer surface of insulation

30°F

Effective thermal conductivity of insulation

0.02 Btu/hr. ft

Heat of eyaporation of oxygen

91.7

Btu/lb

Average

flowing through insulation

0.22 Btu/lb.

Neglect the thermal resistance of the liquid oxygen, container wall, and gas space, and ne-

glect heat losses through the stopper. Assume the particles of insulation to be in local thermal

equilibrium with the gas.

Answers:

82 Btu/hr without transpiration;

Btu/hr with transpiration

llB.8.

Temperature distribution in an embedded sphere. A sphere of radius

and thermal conduc-

tivity

is embedded in an infinite solid of thermal conductivity

ko.

The center of the sphere is

located at the origin of coordinates, and there is a constant temperature gradient

in the posi-

tive

direction far from the sphere. The temperature at the center of the sphere is

To.

The steady-state temperature distributions in the sphere

and in the surrounding

medium

have been shown to be:3

,Tank wall

Fig.

llB.7.

Use of transpiration to reduce the

evaporation rate.

Landau and

Lifshitz,

Fluid

Mechanics,

2nd edition,

Pergamon

Press,

Oxford

(1987),

199.

366

Chapter 11 The Equations of Change for Nonisothermal Systems

Conical

surfaces

I---,

Fig.

11B.9.

Body formed from the intersection of two

cones and a sphere.

(a)

What are the partial differential equations that must be satisfied by Eqs. 11B.8-1 and

(b)

Write down the boundary conditions that apply at

(c)

Show that

and

satisfy their respective partial differential equations in (a).

(d)

Show that

Eqs.

llB.8-1 and

satisfy the boundary conditions in (b).

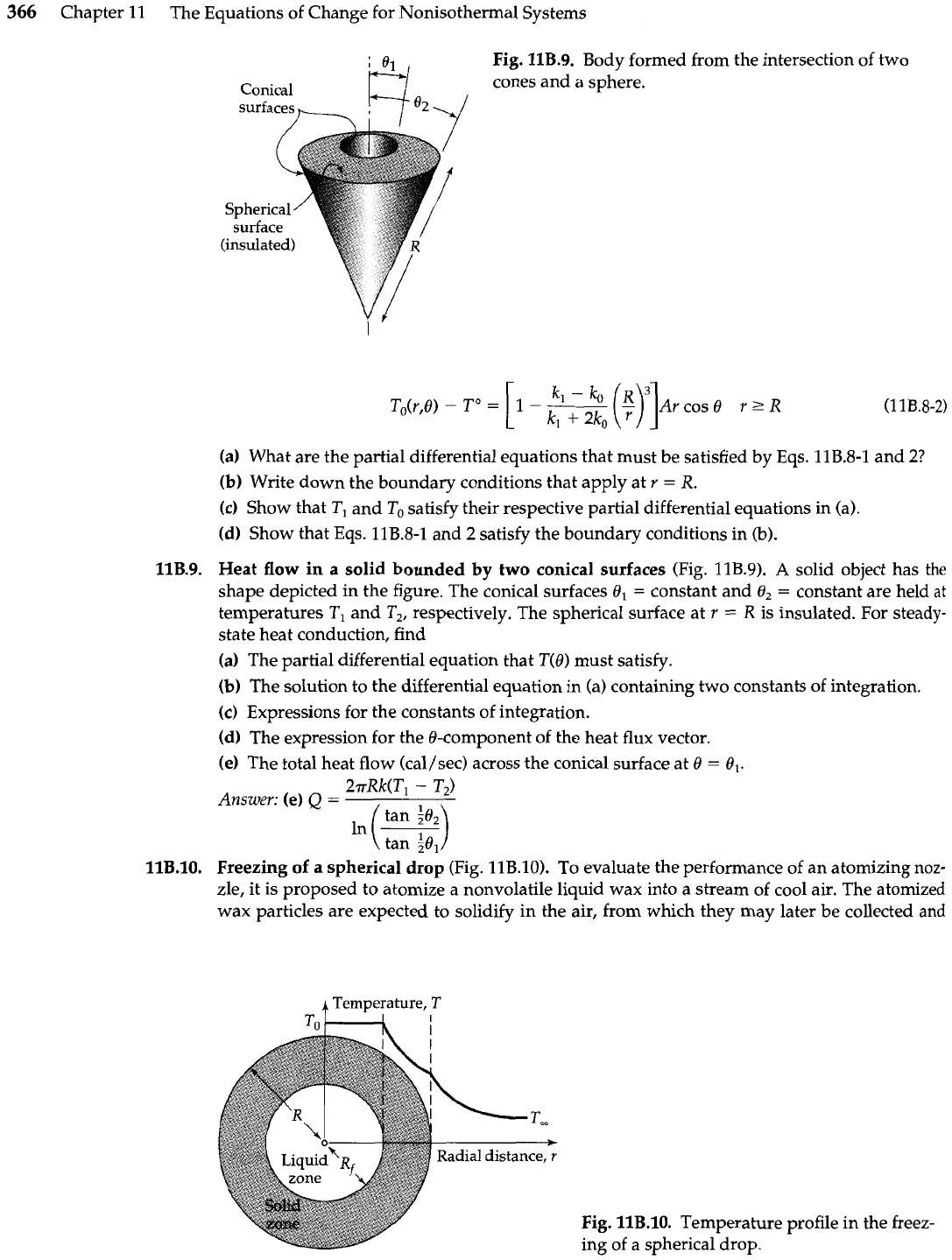
llB.9.

Heat flow in

solid bounded

two conical surfaces

(Fig. 11B.9).

solid object has the

shape depicted

the figure. The conical surfaces

constant and 0,

constant are held

temperatures TI and T,, respectively. The spherical surface at

is insulated. For steady-

state heat conduction, find

(a)

The partial differential equation that T(0) must satisfy.

(b)

The solution to the differential equation in (a) containing two constants of integration.

(c)

Expressions for the constants of integration.

(dl

The expression for the 0-component of the heat flux vector.

(e)

The total heat flow (cal/sec) across the conical surface at 0

0,.

2.rrXk(T1

T2)

Answer:

(e)

11B.10.

Freezing of a spherical drop

(Fig. 118.10). To evaluate the performance of an atomizing noz-

zle, it is proposed to atomize a nonvolatile liquid wax into a stream of cool air. The atomized

wax particles are expected to solidify in the air, from which they may later be collected

and

Fig.

llB.lO.

Temperature profile in the freez-

ing of a spherical drop.