Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena
Подождите немного. Документ загружается.


s12.1 Unsteady Heat Conduction in Solids
377
Hence
Eq.
12.1-14 can be satisfied by
12
2
@,,
=
A,,C,
exp[-(n
+
,)
.rr
TI
cos (n
+
f).rrrl
(12.1-25)
The subscripts
n
remind us that
A
and
C
may be different for each value of n. Because of the
linearity of the differential equation, we may now superpose all the solutions of the form of
Eq.
12.1-25. In doing this we note that the exponentials and cosines for
n
have the same values
as those for -(n
+
I), so that the terms with negative indices combine with those with posi-
tive indices. The superposition then gives
in which
D,
=
A,&,
+
A-(n+l,C-~,+l,.
The
D,,
are now determined by using the initial condition, which gives
Multiplication by cos(m
+
$).rrrl
and integration from
77
=
-1
to 7
=
+1
gives
When the integrations are performed, all integrals on the right side are identically zero, ex-
cept for the term in which
n
=
m.
Hence we get
After inserting the limits, we may solve for
Dm
to get
sin
(m
+
i).rrrl
T
+l
$(m
+
;).rrrl
+
$
sin
2(m
+
$).rrr)
/
=~m
Substitution of this expression into
Eq.
12.1-26 gives the temperature profiles, which we now
rewrite in terms of the original variables2
?=+I
(12.1-29)
The solutions to many unsteady-state heat conduction problems come out as infinite series,
such as that just obtained here. These series converge rapidly for large values2 of the dimen-
sionless time, at/b2. For very short times the convergence is very slow, and in the limit as
cut/b2 approaches zero, the solution in
Eq.
12.1-31 may be shown to approach that given in
Eq.
12.1-8 (see Problem 12D.1). Although
Eq.
12.1-31 is unwieldy for some practical calculations,
a graphical presentation, such as that in Fig. 12.1-1,
is
easy to use (see Problem 12A.3). From
the figure it is clear that when the dimensionless time
r
=
at/b2 is 0.1, the heat has "pene-
trated" measurably to the center plane of the slab, and that at
r
=
1.0 the heating is 90% com-
plete at the center plane.
Results analogous to Fig. 12.1-1 are given for infinite cylinders and for spheres in Figs.
12.1-2 and 3. These charts can also be used to build up the solutions for the analogous heat
conduction problems in rectangular parallelepipeds and cylinders of finite length (see Prob.
12C.1).
(m
+
+)T
~=-1
(m
+
;)a
q=-1
H.
S.
Carslaw and
J.
C. Jaeger,
Conduction
of
Heat
in Solids,
2nd edition, Oxford University Press
(1959),
p.
97,
Eq.
(8);
the alternate solution in
Eq.
(9)
converges rapidly for
small
times.
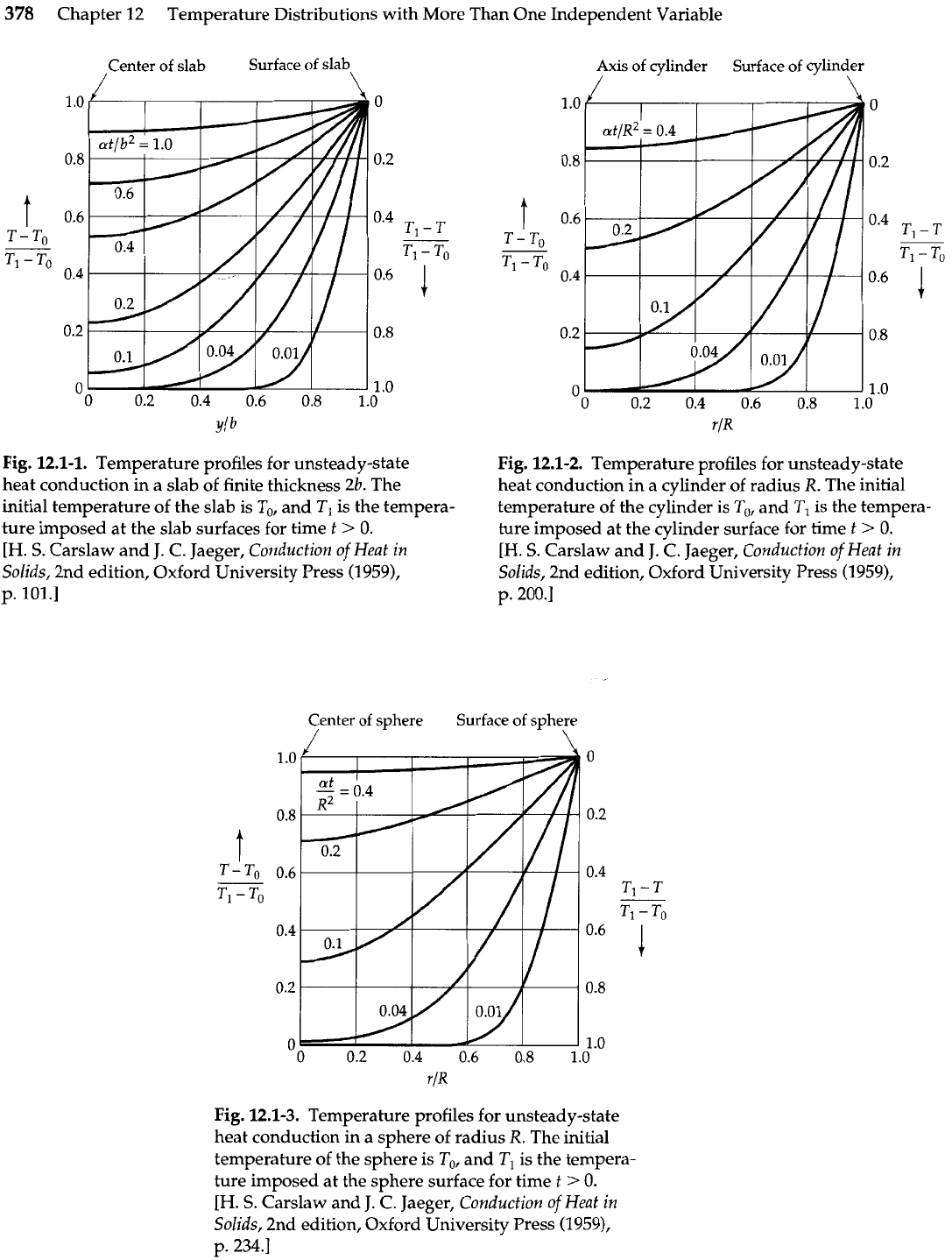
378
Chapter 12 Temperature Distributions with More Than One Independent Variable
Fenter
Of
Surface
of
slab
\
Fig.
12.1-1.
Temperature profiles for unsteady-state
heat conduction in a slab of finite thickness
2b.
The
initial temperature of the slab is To, and T, is the tempera-
ture imposed at the slab surfaces for time t
>
0.
[H.
S.
Carslaw and
J.
C.
Jaeger, Conduction of
Heat
in
Solids, 2nd edition, Oxford University Press (1959),
p. 101.1
Axis of cylinder
Surface
of
cylinder
/
\
Fig.
12.1-2.
Temperature profiles for unsteady-state
heat conduction in a cylinder of radius
R.
The initial
temperature of the cylinder is To, and
TI
is the tempera-
ture imposed at the cylinder surface for time t
>
0.
[H.
S.
Carslaw and
J.
C.
Jaeger, Conduction of
Heat
in
Solids, 2nd edition, Oxford University Press (1959),
p. 200.1
Center of sphere Surface of sphere
/
\
Fig.
12.1-3.
Temperature profiles for unsteady-state
heat conduction in a sphere of radius
R.
The initial
temperature of the sphere is To, and
T1
is the tempera-
ture imposed at the sphere surface for time t
>
0.
[H.
S.
Carslaw and
J.
C. Jaeger, Conduction
of
Heat
in
Solids, 2nd edition, Oxford University Press (1959),
p. 234.1

s12.1 Unsteady Heat Conduction in Solids
379
A
solid body occupying the space from
y
=
0
to
y
=
oo
is initially at temperature
To.
Beginning
at time t
=
0, a periodic heat flux given by
Unsteady Heat
Conduction near
a
q,
=
qo
cos
ot
=
qo%{eiwfl
(12.1-32)
with
Sinusoidal
is imposed at
y
=
0.
Here
q,,
is the amplitude of the heat flux oscillations, and
o
is the (circu-
Heat Flux
lar) frequency. It is desired to find the temperature in this system, T(y, t), in the "periodic
steady state" (see Problem 4.1-3).
SOLUTION
For one-dimensional heat conduction, Eq. 12.1-2 is
Multiplying by
-k
and operating on the entire equation with d/dy gives
or, by making use of 9,
=
-k(dT/dy),
Hence
q,
satisfies the same differential equation as
T.
The boundary conditions are
B.C.
1:
B.C.
2:
This problem is formally exactly the same as that given in Eqs. 4.1-44,46, and 47. Hence the
solution in Eq. 4.1-57 may be taken over with appropriate notational changes:
-
Then by integrating Fourier's law
Substitution of the heat flux distribution into the right side of this equation gives after inte-
gration
Thus, at the surface
y
=
0, the temperature oscillations lag behind the heat flux oscillations by
~/4.
This problem illustrates a standard procedure for obtaining the "periodic steady state" in
heat conduction systems. It also shows how one can use the heat conduction equation in
terms of the heat flux, when boundary conditions on the heat flux are known.
A
homogeneous solid sphere of radius
R,
initially at a uniform temperature
TI,
is suddenly
immersed at time t
=
0
in a volume
Vf
of well-stirred fluid
qf
temperature
To
in an insulated
of
a
tank. It is desired to find the thermal diffusivity
a,
-
ks/psC,,
of the solid by observing the
in Contact with a
change of the fluid temperature Tf with time. We use the following dimensionless variables:
Well-Stirred Fluid
7'1
-
Ts
-
dimensionless solid temperature
@,(5,7)
=
-
-
(12.1-41)
TI
-
To

380
Chapter 12 Temperature Distributions with More Than One Independent Variable
SOLUTION
Tl
-
Tf
Of(d
=
-
=
dimensionless fluid temperature
TI
-
To
Y
,$
=
-
=
dimensionless radial coordinate
R
ffst
T
=
-
=
dimensionless time
x2
The reader may verify that the problem stated in dimensionless variables is
Solid
in which
B
=
pf~plli,/p,~ps~S,
the V's representing the volume of the fluid and of the solid.
Linear problems with complicated boundary conditions and/or coupling between equa-
tions are often solved readily by the Laplace transform method. We now take the Laplace
transform of the preceding equations and their boundary conditions to get:
Fluid
Atr=O,@,
=
0 (12.1-46)
Atc$=
I,@,
=
af
(12.1-47)
At
6
=
0,@,
=
finite (12.1-48)
I
Solid
I
Fluid
I
At7=0,0f=1 (12.1-50)
~tt= l,%=or (12.1-52)
At
5
=
0,@
=
finite (12.1-53)
Here
p
is the transform ~ariable.~ The solution to
Eq.
12.1-51 is
Because of the boundary condition at
,$
=
0,
we must set C, equal to zero. Substitution of this
result into
Eq.
12.1-54 then gives
Next, we insert these last two results into the boundary condition at
5
=
1,
in order to deter-
mine C,. This gives us for
6
We now divide the numerator and denominator within the parentheses
by
p, and take the
in-
verse Laplace transform to get
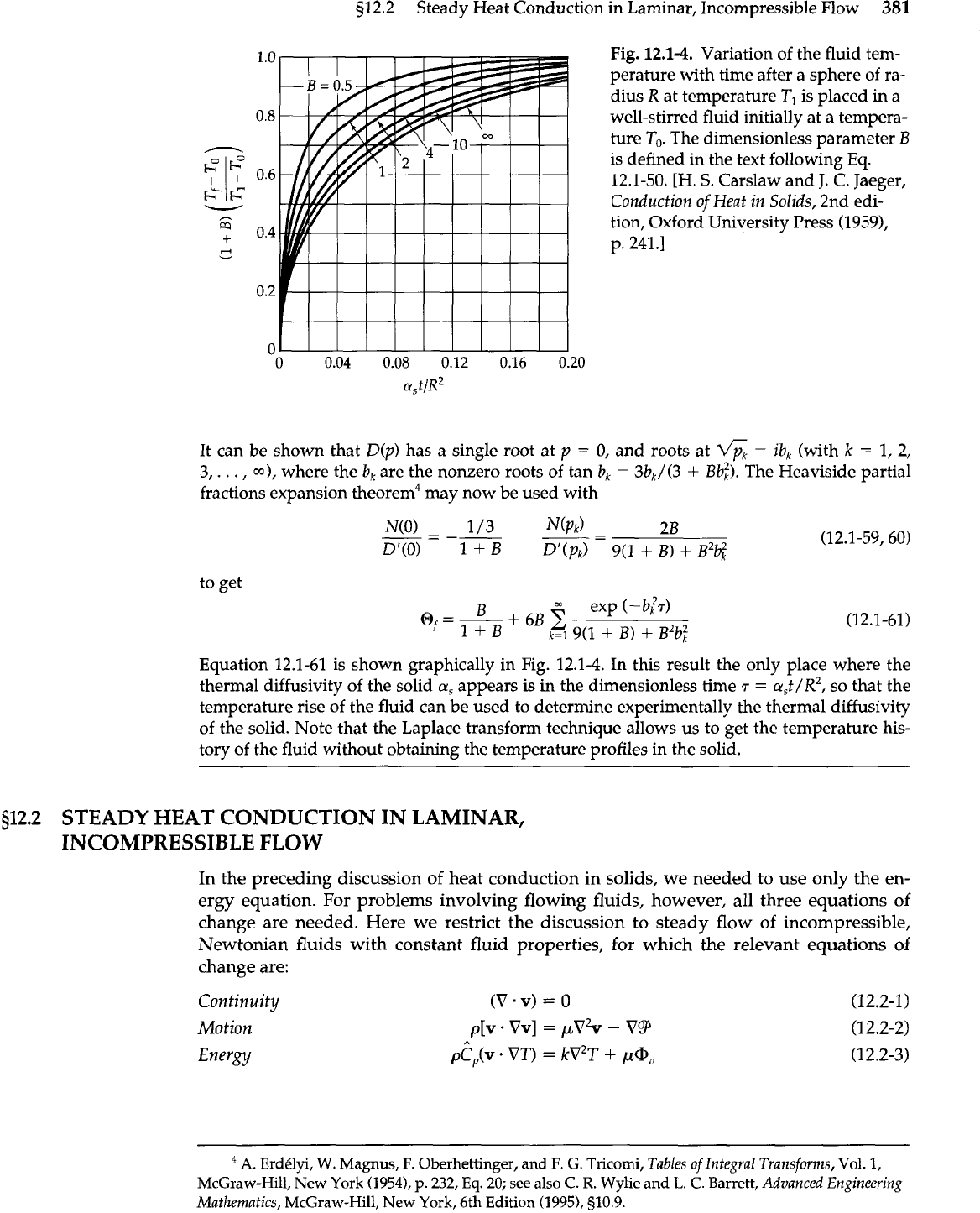
s12.2 Steady Heat Conduction in Laminar, Incompressible Flow
381
Fig.
12.1-4.
Variation of the fluid tem-
perature with time after a sphere of ra-
dius
R
at temperature
T,
is placed in a
well-stirred fluid initially at a tempera-
ture
To.
The dimensionless parameter
B
is defined in the text following
Eq.
12.1-50.
[H.
S.
Carslaw and J.
C.
Jaeger,
Conduction of Heat in Solids, 2nd edi-
tion, Oxford University Press (1959),
p. 241.1
It can
be
shown that
D(p)
has a single root at
p
=
0,
and roots at
V'&
=
ib,
(with
k
=
1, 2,
3,.
. .
,
m),
where the
bk
are the nonzero roots of tan
bk
=
3bk/(3
+
Bb:). The Heaviside partial
fractions expansion theorem4 may now be used with
to get
0
--
+6~5
exp
(-
bk2d
-
1
+
B
,=I
9(1
+
B)
+
B2b:
Equation 12.1-61 is shown graphically in Fig. 12.1-4. In this result the only place where the
thermal diffusivity of the solid
a,
appears is in the dimensionless time
T
=
a,t/R2,
SO
that the
temperature rise of the fluid can be used to determine experimentally the thermal diffusivity
of the solid. Note that the Laplace transform technique allows us to get the temperature his-
tory of the fluid without obtaining the temperature profiles in the solid.
512.2
STEADY HEAT
CONDUCTION
IN
LAMINAR,
INCOMPRESSIBLE
FLOW
In the preceding discussion of heat conduction in solids, we needed to use only the en-
ergy equation. For problems involving flowing fluids, however, all three equations of
change are needed. Here we restrict the discussion to steady flow of incompressible,
Newtonian fluids with constant fluid properties, for which the relevant equations of
change are:
Continuity
Motion
Energy
(V
v)
=
0
p[v
.
VV]
=
-
VP
p@v.
VT)
=
kV2~
+
pa,
A.
Erdelyi,
W.
Magnus,
F.
Oberhettinger, and
F.
G. Tricomi,
Tables of Integral Transforms,
Vol.
1,
McGraw-Hill, New York (1954),
p.
232,
Eq.
20; see also
C.
R.
Wylie and
L.
C.
Barrett,
Advanced Engineering
Mathematics,
McGraw-Hill, New York,
6th
Edition (1995), s10.9.

382
Chapter
12
Temperature Distributions with More Than One Independent Variable
In Eq. 12.2-3,
a,
is the dissipation function given in Eq. 3.3-3. To get the temperature
profiles for forced convection, a two-step procedure is used: first Eqs. 12.2-1 and 2 are
solved to obtain the velocity distribution v(r,
t);
then the expression for v is substi-
tuted into Eq. 12.2-3, which may in turn be solved to get the temperature distribution
T(r,
t).
Many analytical solutions of Eqs. 12.2-1 to 3 are available for commonly encoun-
tered
situation^.'-^.
One of the oldest forced-convection problems is the Graetz-Nusselt
problem,' describing the temperature profiles in tube flow where the wall temperature
undergoes a sudden step change at some position along the tube (see Problems
12D.2, 3, and
4).
Analogous solutions have been obtained for arbitrary variations of
wall temperature and wall flux.9 The Graetz-Nusselt problem has also been extended
to non-Newtonian fluids.'' Solutions have also been developed for a large class
of
laminar heat exchanger problems,ll in which the wall boundary condition is provided
by the continuity of heat flux across the surfaces separating the two streams. A fur-
ther problem of interest is duct flow with significant viscous heating effects (the
Brinkman problem12).
In this section we extend the discussion of the problem treated in §10.8-namely, the
determination of temperature profiles for laminar flow of an incompressible fluid in
a
circular tube. In that section we set up the problem and found the asymptotic solution
for distances far downstream from the beginning of the heated zone. Here, we give the
complete solution to the partial differential equation as well as the asymptotic solution
for short distances. That is, the system shown in Fig. 10.8-2 is discussed from three view-
points in this book:
a.
Complete solution of the partial differential equation by the method of separa-
tion of variables (Example 12.2-1).
b.
Asymptotic solution for short distances down the tube by the method of combi-
nation of variables (Example 12.2-2).
c.
Asymptotic solution for large distances down the tube (s10.8).
'
M.
Jakob,
Heat Transfer,
Vol.
I,
Wiley, New York (1949), pp. 451464.
H.
Grober,
S.
Erk, and
U.
Grigull,
Die Grundgesetze der Wiivmeiiberfragung,
Springer, Berlin (1961),
Part
11.
'
R.
K.
Shah and A. L. London,
Laminar Flow Forced Convection in Ducts,
Academic Press, New York
(1978).
L.
C.
Burmeister,
Convective Xeat Transfer,
Wiley-Interscience, New York (1983).
L.
D.
Landau and
E.
M.
Lifshitz,
Fluid Mechanics,
Pergamon, Oxford (1987), Chapter 5.
L.
G. Leal,
Laminar Flow and Convective Transport Processes,
Butterworth-Heinemann (1992),
Chapters 8 and 9.
W.
M.
Deen,
Analysis of Transport Phenomena,
Oxford University Press (1998), Chapters 9
and 10.
L.
Graetz,
Ann. Pkys.
(N.F.),
18, 79-94 (1883), 25,337-357 (1885); W. Nusselt,
Zeits. Ver. deutch. Ing.,
54,11541158 (1910). For the "extended Graetz problem," which includes axial conduction, see
E.
Papoutsakis,
D.
Ramkrishna, and
H.
C. Lim,
Appl.
Sci. Res.,
36,13-34 (1980).
E.
N.
Lightfoot,
C.
Massot, and
F.
Irani,
Chem. Eng. Progress Symp. Series,
Vol. 61, No. 58 (1965),
pp. 28-60.
B.
Bird,
R.
C. Armstrong, and
0.
Hassager,
Dynamics of Polymeric Liquids,
Wiley-Interscience
(1987),
2nd
edition, Vol. 1, g4.4.
"
R.
J.
Nunge and W.
N.
Gill,
AIChE Journal,
12,279-289 (1966).
l2
H.
C.
Brinkman,
Appl. Sci. Research,
A2,120-124 (1951);
R.
B. Bird,
SPE Journal,
11,3540 (1955);
H.
L. Toor,
Ind. Eng. Chem.,
48,922-926 (1956).

512.2 Steady Heat Conduction in Laminar, Incompressible Flow
383
Solve Eq. 10.8-19 with the boundary conditions given in Eqs. 10.8-20,21, and 22.
Laminar Tube Flow
with Constant Heat
SOLUTION
Flux at the Wall
The complete solution for the temperature is postulated to be of the following form:
in which Om((,
l)
is the asymptotic solution given in Eq. 10.8-31, and Od((, 5) is a function that
will be damped out exponentially with
5.
By substituting the expression for
@(&
5)
in Eq. 12.2-
4
into Eq. 10.8-19, it may be shown that the function Od(&
5)
must satisfy
Eq.
10.8-19 and also
the following boundary conditions:
B.C. 1:
B.C.
2:
B.C. 3: at
l=
0, Od
=
Om(& 0) (12.2-7)
We anticipate that a solution to the equation for O&,
will be factorable,
Then Eq. 10.8-19 can be separated into two ordinary differential equations
in which
-c2
is the separation constant. Since the boundary conditions on
X
are
dX/dt
=
0 at
6
=
0,
1,
we have a Sturm-Liouville problem.13 Therefore we know there will be an infinite
number of eigenvalues
ck
and eigenfunctions
Xk,
and that the final solution must be of the
form:
where
The
problem is thus reduced to finding the eigenfunctions
Xk(O
by solving Eq. 12.2-10, and
then getting the eigenvalues
ck
by applying the boundary condition at
6
=
1.
This has been
done for
k
up to
7
for this problem.14
l3
M.
D.
Greenberg,
Advanced Engineering Mathematics,
Prentice-Hall, Upper Saddle River,
N.J.,
Second Edition
(1998),
s17.7.
I%.
Siegel, E.
M.
Sparrow, and
T.
M.
Hallman,
Appl. Sci. Research,
A7,386-392
(1958).

384
Chapter 12 Temperature Distributions with More Than One Independent Variable
Note that the sum in Eq. 12.2-11 converges rapidly for large
z
but slowly for small
z.
Develop
an expression for T(r,
z)
that is useful for small values.
Laminar Tube Flow
with Constant Heat
Flux at the Wall:
~~~~~~i~ solution
For small
z
the heat addition affects only a very thin region near the wall, so that the follow-
for
the
Region
ing three approximations lead to results that are accurate in the limit as
z
+
0:
a.
Curvature effects may be neglected and the problem treated as though the wall were
flat; call the'distance from the wall
y
=
R
-
r.
b.
The fluid may be regarded as extending from the (flat) heat transfer surface
(y
=
0)
to
y
=
m.
c.
The velocity profile may be regarded as linear, with a slope given by the slope of the
parabolic velocity profile at the wall: v,(y)
=
voy/R, in which v,
=
(Po
-
P,)R2/2p~.
This is the way the system would appear to a tiny "observer" who is located within the very
thin shell of heated fluid. To this observer, the wall would seem flat, the fluid would appear
to be of infinite extent, and the velocity profile would seem to be linear.
The energy equation then becomes, in the region just slightly beyond
z
=
0,
Actually it is easier to work with the corresponding equation for the heat flux in the
y
direc-
tion
(q,
=
-k
dT/dy).
This
equation is obtained by dividing Eq. 12.2-13 by
y
and differentiat-
ing with respect to
y:
It is more convenient to work with dimensionless variables defined as
Then Eq. 12.2-14 becomes
with these boundary conditions:
B.C.
1:
B.C. 2:
B.C. 3:
ath
=0,
Q=O
atq=O, $=I
asv+m,
Q+O
This problem can be solved by the method of combination of variables (see Examples 4.1-1
and 12.1-1) by using the new independent variable
x
=
v/$"%.
Then Eq. 12.2-16 becomes
The boundary conditions are: at
x
=
0,
IC,
=
1,
and as
x
+
m,
Q
+
0. The solution of Eq. 12.2-20
is found by first letting d+/dx
=
p,
and getting a first-order equation for
p.
The equation for
p
can be solved and then
I)
is obtained as

512.3 Steady Potential Flow of Heat in Solids
385
The temperature profile may then be obtained by integrating the heat flux:
or, in dimensionless form,
Then the expression for
cC,
is inserted into the integral, and the order of integration in the dou-
ble integral can be reversed (see Problem
12D.7).
The result is
Here
r($)
is the (complete) gamma function, and
r($,
X3)
is an incomplete gamma function.15
To compare this result with that in Example 12.2-1, we note that
17
=
1
-
8
and
A
=
if.
The di-
mensionless temperature is defined identically in 510.8, in Example 12.2-1, and here.
812.3
STEADY
POTENTIAL
FLOW OF
HEAT
IN
SOLIDS
The steady flow of heat in solids of constant thermal conductivity is described by
Fourier's
law
q
=
-kVT
Heat conduction equation
V2T
=
0
These equations are exactly analogous to the expression for the velocity in terms of the
velocity potential
(v
=
-V+),
and the Laplace equation for the velocity potential
(V24
=
0), which we encountered in
54.3.
Steady heat conduction problems can therefore be
solved by application of potential theory.
For two-dimensional heat conduction in solids with constant thermal conductivity,
the temperature satisfies the two-dimensional Laplace equation:
We now use the fact that any analytic function w(z)
=
fix,
y)
+
ig(x,
y)
provides two scalar
functions f and
g,
which are solutions of Eq.
12.3-3.
Curves off
=
constant may be interpreted
as lines of heat flow, and curves of
g
=
constant are the corresponding isothermals for
some
heat flow problems. These two sets of curves are orthogonal-that
is,
they intersect at right
angles. Furthermore, the components of the heat flux vector at any point are given by
Given an analytic function, it is easy to find heat flow problems that are described by it.
But the inverse process of finding an analytic function suitable for a given heat flow
problem is generally very difficult. Some methods for this are available, but they are out-
side the scope of this textbook.',*
l5
M.
Abramowitz and
I.
A. Stegun, eds.,
Handbook
of
Mathematical Functions,
Dover, New York,
9th
Printing
(1973),
pp. 255
et
seq.
'
H.
S.
Carslaw and
J.
C. Jaeger,
Conduction
of Heat
in Solids,
2nd edition, Oxford University Press
(1959),
Chapter
XVI.
M. D.
Greenberg,
Advanced Engineering Mathematics,
Prentice-Hall, Upper Saddle
River,
N.J.,
2nd
Edition
(19981,
Chapter
22.

386
Chapter 12
Temperature Distributions with More Than One Independent Variable
For every complex function w(z), two heat flow nets are obtained by interchanging
the lines of constant
f
and the lines of constant
g.
Furthermore, two additional nets are
obtained by working with the inverse function z(w) as illustrated in Chapter 4 for ideal
fluid flow.
Note that potential fluid flow and potential heat flow are mathematically similar, the
two-dimensional flow nets in both cases being described by analytic functions. Physi-
cally, however, there are certain important differences. The fluid flow nets described
in
54.3 are for a fluid with no viscosity (a fictitious fluid!), and therefore one cannot use
them to calculate the drag forces at surfaces. On the other hand, the heat flow nets de-
scribed here are for solids that have a finite thermal conductivity, and therefore the
re
sults can be used to calculate the heat flow at all surfaces. Moreover, both the velocity
components (in Cartesian coordinates!) of 54.3 and the temperature profiles of this sec-
tion satisfy the Laplace equation. Further information about analogous physical pro-
cesses described by the Laplace equation is available in books on partial differential
eq~ations.~
Here we give just one example to provide a glimpse of the use of analytic functions;
further examples may be found in the references cited.
Consider a wall of thickness
b
extending from
0
to
w
in they direction, and from
-
co
to
+w
in
the direction perpendicular to the x and
y
directions (see Fig. 12.3-1). The surfaces at x
=
+ib
Temperature
are held at temperature To, whereas the bottom of the wall at the surface y
=
0
is maintained
Distribution
at temperature
T,.
Show that the imaginary part of the function4
in
a
Wall
SOLUTION
(sin m/b)
-
1
(sin m/b)
+
1
gives the steady temperature distribution
Wx,
y)
=
(T
-
To)/(Tl
-
To).
The imaginary part of
w(z)
in
Eq.
12.3-5 is
~(x, y)
=
,
arctan
(E;;!)
in which the arctangent
is
in the range from
0
to
:.
When x
=
+fb,
Eq.
12.3-6
gives O
=
0,
and
when
y
=
0,
it gives
O
=
(2/d arctan
=
1.
Fig.
12.3-1.
Steady two-dimensional temper-
T=T1orO=l
ature distribution in a wall.
I.
N.
Sneddon,
Elements of Partial Differential Equations,
Dover,
New York
(1996),
Chapter
4.
R.
V.
Churchill,
Introduction to Complex Variables and Applications,
McGraw-Hill, New York
(1948),
Chapter
IX.
See also
C.
R.
Wylie and
L.
C.
Barrett,
Advanced Engineering Mathematics,
McGraw-Hill, New
York,
6th
Edition
(1995),
Chapter
20.
