Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

Problems

397

(d)

Then solve the equation for g(77).

(e) Finally, evaluate the constant

C,,

and thereby complete the derivation of the temperature

distribution.

12B.3.

Heating of a wall (constant wall heat

flux).

A very thick solid wall is initially at the tempera-

ture

To.

At time

a constant heat flux

is applied to one surface of the wall (at

O),

and this heat flux is maintained. Find the time-dependent temperature profiles T(y, I) for

small times. Since the wall is very thick it can be safely assumed that the two wall surfaces are

an infinite distance apart in obtaining the temperature profiles.

(a) Follow the procedure used

going from Eq. 12.1-33 to Eq. 12.1-35, and then write the ap-

propriate boundary and initial conditions. Show that the analytical solution of the problem is

(b)

Verify that the solution is correct by substituting it into the one-dimensional heat conduc-

tion equation for the temperature (see Eq. 12.1-33). Also show that the boundary and initial

conditions are satisfied.

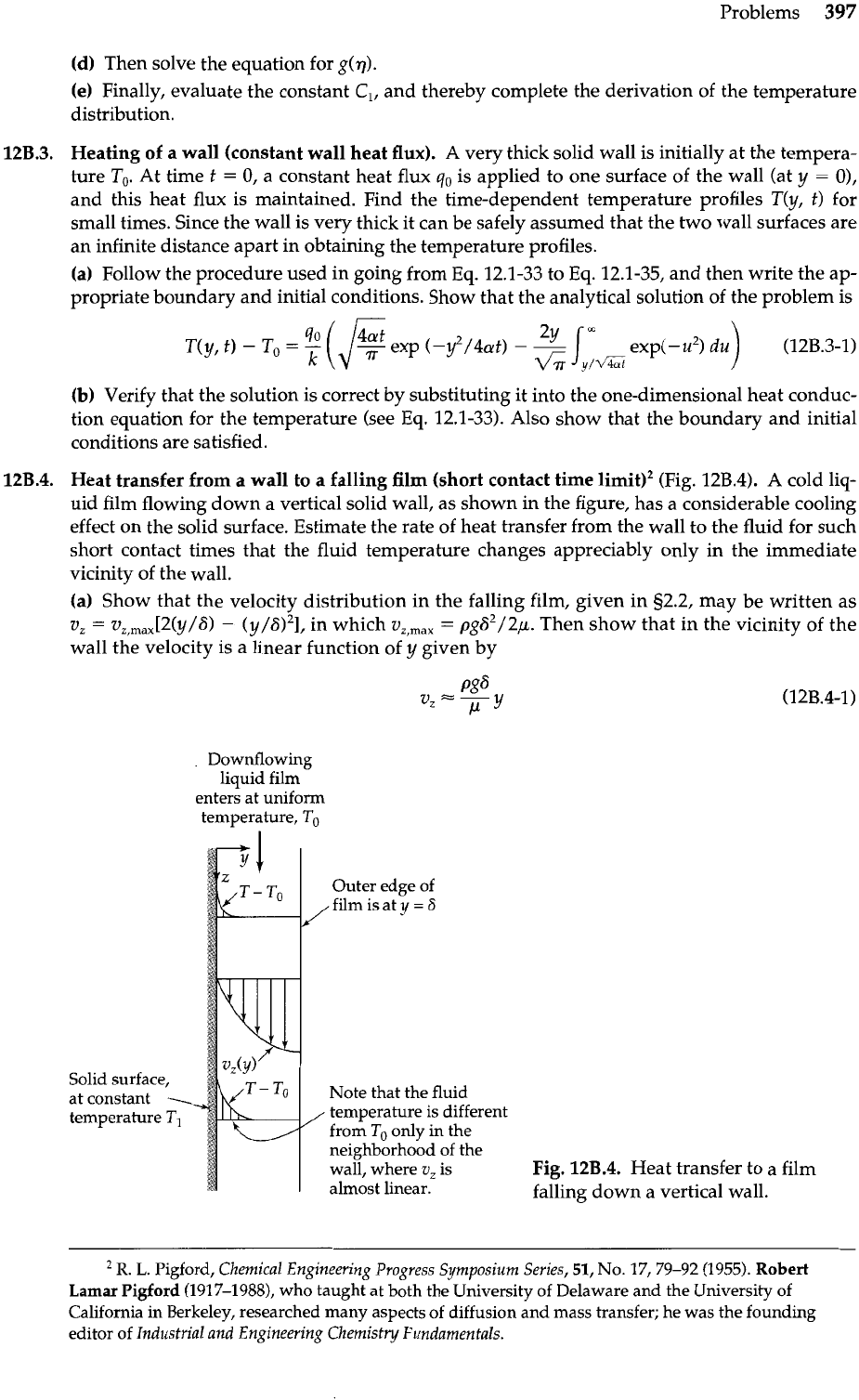
12B.4.

Heat transfer from a wall to a falling film (short contact time limitI2 (Fig. 12B.4).

cold liq-

uid film flowing down a vertical solid wall, as shown in the figure, has a considerable cooling

effect on the solid surface. Estimate the rate of heat transfer from the wall to the fluid for such

short contact times that the fluid temperature changes appreciably only in the immediate

vicinity of the wall.

(a) Show that the velocity distribution in the falling film, given in 52.2, may be written as

vZ,,,,[2(y/6)

(y/6)2], in which

v,,,,

pg13~/2~. Then show that in the vicinity of the

wall the velocity is a linear function of

given by

Downflowing

liquid film

enters at uniform

temperature,

Outer edge of

film is at

Note that the fluid

temperature is different

from

only in the

neighborhood of the

wall, where

almost linear.

Fig.

12B.4.

Heat transfer to a film

falling down a vertical wall.

Pigford,

Chemical Engineering Progress Symposium Series,

51,

No. 17,79-92 (1955).

Robert

Lamar Pigford

(1917-1988), who taught at both the University of Delaware and the University of

California in Berkeley, researched many aspects of diffusion and mass transfer; he was the founding

editor of

Industrial and Engineering Chemisty Fundamentals.

398

Chapter 12 Temperature Distributions with More Than One Independent Variable

(b)

Show that the energy equation for this situation reduces to

List all the simplifying assumptions needed to get this result. Combine the preceding two

equations to obtain

in which

pk/p2?pgt3.

(c)

Show that for short contact times we may write as boundary conditions

B.C. 1:

B.C. 2:

B.C. 3:

T=To forz=O

and

y>O

for

and z finite

T=T, fory=O and z>0

Note that the true boundary condition at

is replaced by a fictitious boundary condition

at y

This is possible because the heat is penetrating just a very short distance into the

fluid.

(d)

Use the dimensionless variables

W77)

To)/(Tl

To) and

y/m

to rewrite

the differential equation as (see

Eq.

C.l-9):

Show that the boundary conditions are

0 for

and

at 7

(el

In Eq. 12B.4-7, set dO/dq

p and obtain an equation for p(rl). Solve that equation to get

d@/dq

p(7)

exp

(FT3).

Show that a second integration and application of the bound-

ary conditions give

(f)

Show that the average heat flux to the fluid is

where use is made of the Leibniz formula in sC.3.

Temperature in a slab with heat production.

The slab of thermal conductivity

in Example

12.1-2 is initially at a temperature

To.

For time

there is a uniform volume production

heat

within the slab.

(a)

Obtain an expression for the dimensionless temperature k(T

To)/Sob2 as a function of

the dimensionless coordinate

y/b and the dimensionless time by looking up the solution

in the book by Carslaw and Jaeger.

(b)

What is the maximum temperature reached at the center of the slab?

(c)

How much time elapses before 90% of the temperature rise occurs?

Answer:

(c)

b2/a

Forced convection in slow flow across a cylinder

(Fig. 12B.6).

long cylinder of radius

suspended in an infinite fluid of constant properties

and

The fluid approaches with

Problems

399

Fluid approaches

with velocity

and temperature

urface of cylinder at

uniform temperature

Fig.

12B.6.

Heat transfer from a long

cylinder of radius R.

temperature

and velocity

v,.

The cylindrical surface is maintained at temperature

To.

For

this system the velocity distribution has been determined by Lamb3 in the limit of Re

His result for the region close to the cylinder is

in which

1(1

is the first polar-coordinate stream function in Table 4.2-1. The dimensionless

quantity

is given by

ln(8/Re), where

0.5772.

is "Euler's constant," and

Dv,p/p.

(a)

For this system, determine the interfacial velocity gradient

defined in Example 12.4-3.

(b)

Determine the rate of heat loss

from a length

of the cylinder using the method of

Ex-

ample 12.4-3. Note that

where

B(m,

r(m)r(n)/r(m

is the "beta function."

(c)

Determine S,/R at

in-,

and

n-.

2v, sin

Answers:

(a)

TJ($)(Y)"~

(Evaluate the constant

(,-)!T=

(s)

f(8);f

($)1/3,1.1981,m

R RePr

12B.7.

Timetable

for

roasting turkey

(a)

homogeneous solid body of arbitrary shape is initially at temperature

throughout.

it is immersed in a fluid medium of temperature

T,.

Let

be a characteristic length in

the solid. Show that dimensional analysis predicts that

O(5'

and geometrical ratios) (12B.7-1)

where O

T,)/(T,

To),

x/L,

y/L,

z/L,

and

at/^'.

Relate this result to

the graphs given in 512.1.

Lamb,

Phil.

Mag.,

(6) 21,112-110 (1911). For a survey of more detailed analyses, see

Rosenhead (ed.),

Laminar

Boundary

Layers,

Oxford University Press, London (19631, Chapter

400

Chapter 12

Temperature Distributions with More Than One Independent Variable

(b)

typical timetable for roasting turkey at

350°F

is4

Mass of turkey

Time required per unit mass

(lb,) (min/lb,)

Compare this empirically determined cooking schedule with the results of part (a), for geo-

metrically similar turkeys at an initial temperature To, cooked with a given surface tempera-

ture T, to the same dimensionless temperature distribution

@(<,

[).

Use of asymptotic boundary layer solution. Use the results of Ex. 12.4-2 to obtain 6, and

for the system in Problem 12D.4. By comparing ST with

estimate the range of applicability

of the solution obtained in Problem 12D.4.

Non-Newtonian heat transfer with constant wall heat flux (asymptotic solution for small

axial

distances). Rework Example 12.2-2 for

fluid whose non-Newtonian behavior is described ade

quately by the power law model. Show that the solution given in Eq. 12.2-2 may be taken over

for the power law model simply by an appropriate modification in the definition of

v,.

Product solutions for unsteady heat conduction in solids.

(a) In Example 12.1-2 the unsteady state heat conduction equation is solved for a slab of

thickness 2b. Show that the solution to Eq. 12.1-2 for the analogous problem for a rectangular

block of finite dimensions

2a,

2b, and 2c may be written as the product of the solutions for

three slabs of corresponding dimensions:

in which @(y/b, at/b2) is the right side of Eq. 12.1-31.

(b) Prove a similar result for cylinders of finite length; then rework Problem 12A.4 without

the assumption that the cylinder is infinitely long.

Heating of

semi-infinite slab with variable thermal conductivity. Rework Example 12.1-1

for a solid whose thermal conductivity varies with temperature as follows:

in which

is the thermal conductivity at temperature To, and

is a constant. Use the follow-

ing approximate procedure:

(a) Let

T,)/(T,

To) and

y/S(t), where S(t) is a boundary layer thickness that

changes with time. Then assume that

in which the function @(q) gives the shapes of the "similar" profiles. This is tantamount to

as-

suming that the temperature profiles have the same shape for all values of

which, of

course, is not really true.

(b) Substitute the above approximate profiles into the heat conduction equation and obtain

the following differential equation for the boundary layer thickness:

Woman's Home Companion Cook Book,

Garden

City

Publishing Co.,

(19461,

courtesy

Jean Stewart.

Problems

401

in which

ko/pC, and

Then solve for the function

S(t).

(c)

Now let

@(v)

z7)

iq3.

Why is this a felicitous choice? Then find the time-depen-

dent temperature distribution T(y, t) as well as the heat flux at y

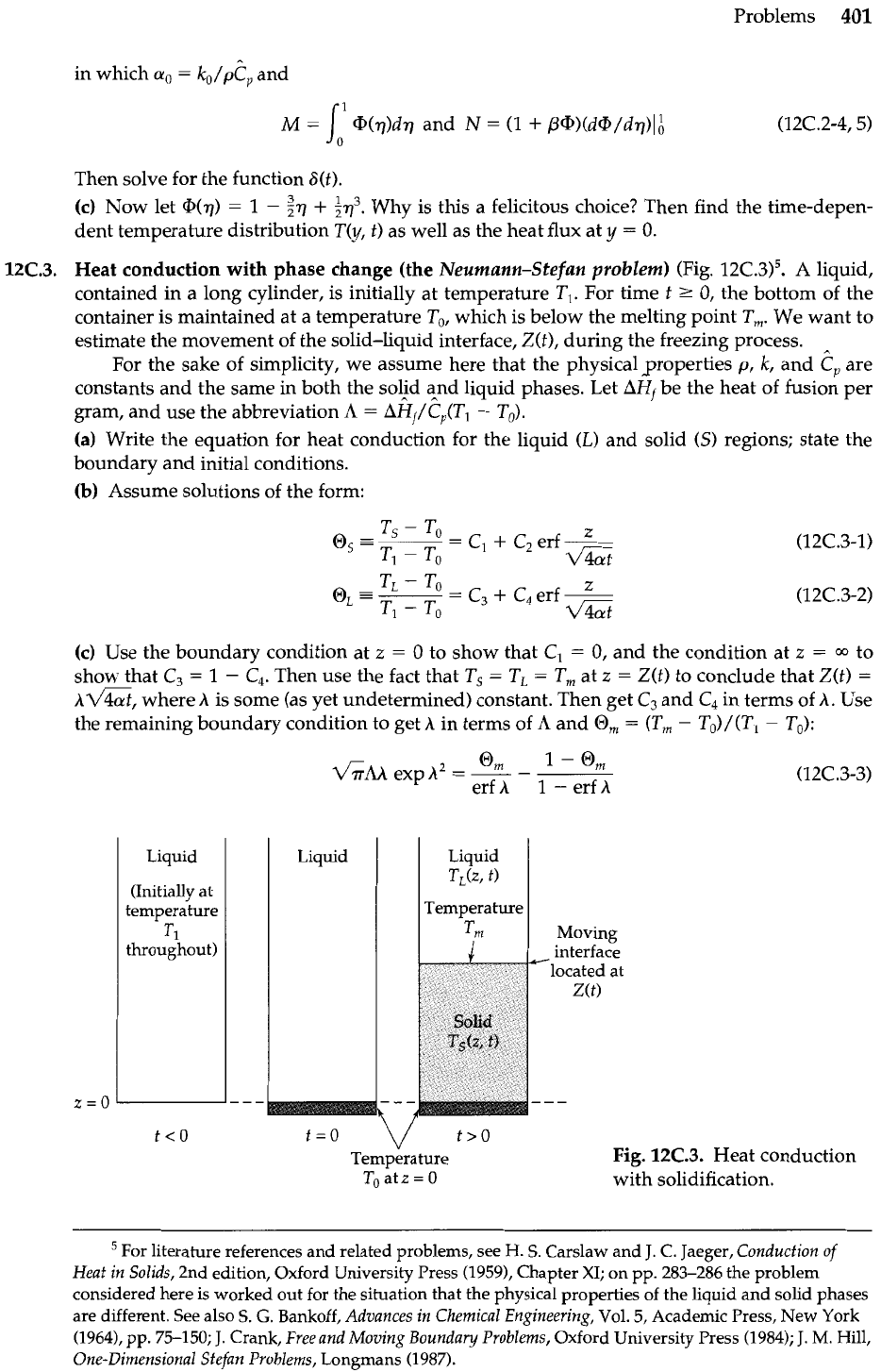
12C.3.

Heat conduction with phase change (the

Neumann-Stefan problem)

(Fig. 12C.3)5. A liquid,

contained in a long cylinder, is initially at temperature T,. For time t

the bottom of the

container is maintained at a temperature To, which is below the melting point

T,.

We want to

estimate the movement of the solid-liquid interface, Z(t), during the freezing process.

For the sake of simplicity, we assume here that the physicalgroperties p,

and C, are

constants and the same in both the soljd zpd liquid phases. Let AHf be the heat of fusion per

gram, and use the abbreviation

AHf/C,(T,

To).

(a) Write the equation for heat conduction for the liquid

(L)

and solid

(S)

regions; state the

boundary and initial conditions.

(b)

Assume solutions of the form:

(c)

Use the boundary condition at

to show that

and the condition at

show that

C4. Then use the fact that

T, at

Z(t) to conclude that Z(t)

A-,

where h is some (as yet undetermined) constant. Then get Cg and

in terms of A. Use

the remaining boundary condition to get

in terms of

and

(T,

To)/(T,

To):

Liquid

(Initially at

temperature

throughout)

6hh

exph2

erf

Liquid

t=O

t>O

Temperature

Liquid

TLk,

Temperature

=?,I

..-

interfa&

located at

Z(t)

Moving

Fig.

12C.3.

Heat conduction

with solidification.

For literature references and related problems, see

Carslaw

and

Jaeger,

Conduction of

Heat in

Solids,

2nd edition, Oxford University Press (1959), Chapter

XI;

on pp. 283-286 the problem

considered here is worked out for the situation that the physical properties of the liquid and solid phases

are different. See also

Bankoff,

Advances in Chemical Engineering,

Vol.

Academic Press, New York

(1964), pp.

75-150;

Crank,

Free and Moving Bounda

Problems,

Oxford University Press (1984);

Hill,

One-Dimensional Stefan Problems,

Longmans (1987).

402

Chapter 12

Temperature Distributions with More Than One Independent Variable

What is the final expression for

Z(t)?

(Note: In this problem it has been assumed that a phase

change occurs instantaneously and that no supercooling of the liquid phase occurs. It turns

out that in the freezing of many liquids, this assumption is untenable. That is, to describe the

solidification process correctly, one has to take into account the kinetics of the crystallization

pro~ess.~)

12C.4.

Viscous heating in oscillatory flow.7 Viscous heating can be a disturbing factor

viscosity

measurements. Here we see how viscous heating can affect the measurement of viscosity in

an oscillating-plate system.

Newtonian fluid is located in the region between two parallel plates separated by a

distance b. Both plates are maintained at a temperature To. The lower plate (at

is made

to oscillate sinusoidally in the

direction with a velocity amplitude vo and a circular fre-

quency

Estimate the temperature rise resulting from viscous heating. Consider only the

high-frequency limit.

(a) Show that the velocity distribution is given by

sinh a(l

cos a(l

sinh a cos a

cos ot

sin a(l

cosh a(l

sin a cosh

sin a(l

cosh a(l

sinh a cos

sin ot

v,(x,

+sinh a(1

cos a(1

sin a cosh a

(12C.4-1)

sinh2 a cos a

cosh2 a sin

where

dPwb2/2p and

(b)

Next calculate the dissipation function

for the velocity profile in Eq. 12C.4-1. Then

ob-

tain

time-averaged dissipation function

&,,

by averaging over one cycle. Use the formulas

cos2 wt

sin2

and sin

cos wt

(12C.4-2)

which may be verified. Then simplify the result for high frequencies (i.e., for large values of

to obtain

(c)

Next take a time average of the heat conduction equation to obtain

in which is the temperature averaged over one cycle. Solve this to get

This shows how the temperature in the slit depends on position. From this function, the max-

imum temperature rise can be calculated. For reasonably high frequencies,

pv;/4k.

12C.5.

Solar heat penetration. Many desert animals protect themselves from excessive diurnal tem-

perature fluctuations by burrowing sufficiently far underground that they can maintain

Janeschitz-Kriegl,

Plastics and Rubber Processing and Applications,

4,145-158 (1984);

Janeschitz-Kriegl, in

One-Hundred Years of Chemical Engineering

(N. A. Peppas, ed.), Kluwer Academic

Publishers, Dordrecht (Netherlands) (1989), pp. 111-124;

Janeschitz-Kriegl,

Ratajski, and G. Eder,

Ind. Eng. Chem. Res.,

34,3481-3487 (1995);

Astarita and

Kenny,

Chem. Eng. Comm.,

53,6944

987).

Bird,

Chem. Eng. Prog. Symposium Series,

Vol. 61, No. 58 (1965), pp. 13-14; see also

Ding,

Giacomin,

Bird, and

C-B

Kweon, J.

Non-Newtonian Fluid Mech.,

86,359-374 (1999).

Problems

403

themselves at a reasonably steady temperature. Let the temperature in the ground be T(y, t),

where

is the depth below the surface of the earth and t is the time, measured from the time

of maximum temperature To. Further, let the temperature far beneath the surface be

T,,

and

let the surface temperature be given by

T(0, t)

for t

T(0, t)

(To

T,) cos ot

for t

0 (12C.5-1)

Here

2n-/t,,,, in which tp,, is the time for one full cycle of the oscillating temperature

namely, 24 hours. Then it can be shown that the temperature at any depth is given by

This equation is the heat conduction analog of

Eq.

4D.1-1, which describes the response of the

velocity profiles near an oscillating plate. The first term describes the "periodic steady state"

and the second the "transient" behayior. Assume the following properties for the soil:'

1515 kg/m"

0.027 W/m K, and

800 J/kg. K.

(a)

Assume that the heating of the earth's surface is exactly sinusoidal, and find the ampli-

tude of the temperature variation beneath the surface at a distance y. To do this, use only the

periodic steady state term in Eq. 12C.5-2. Show that at a depth of 10 cm, this amplitude has

the value of 0.0172.

(b)

Discuss the importance of the transient term in

Eq.

12C.5-2. Estimate the size of this con-

tribution.

(c)

Next consider an arbitrary formal expression for the daily surface temperature, given as a

Fourier series of the form

T(0, t)

(an

cos

not

sin not)

n=O

How many terms in this series are used to solve part (a)?

12C.6.

Heat transfer in a falling non-Newtonian film.

Repeat Problem 12B.4 for a polymeric fluid

that is reasonably well described by the power law model of

Eq.

8.3-3.

12D.1.

Unsteady-state heating

a slab (Laplace transform method).

(a)

Re-solve the problem in Example 12.1-2 by using the Laplace transform, and obtain the

result in

Eq.

12.1-31.

(b)

Note that the series in

Eq.

12.1-31 does not converge rapidly at short times. By inverting

the Laplace transform in a way different from that in (a), obtain a different series that is

rapidly convergent for small times9

(c)

Show how the first term in the series in (b) is related to the "short contact time" solution

of Example 12.1-1.

12D.2.

The

Graetz-Nusselt problem

(Table 12D.2).

(a)

A fluid (Newtonian or generalized Newtonian) is in laminar flow in a circular tube of ra-

dius

In the inlet region

0, the fluid temperature is uniform at T,. In the region

0, the

wall temperature is maintained at To. Assume that all physical properties are constant and

Rohsenow,

Hartnett, and

Cho, eds.,

Handbook of Heat Transfer,

3rd edition,

McGraw-Hill

(1998),

2.68.

Carslaw and

Jaeger,

Conduction of Heat

Solids,

2nd

edition, Oxford University Press

(1959),

pp.

308-310.

404

Chapter 12 Temperature Distributions with More Than One Independent Variable

that viscous dissipation and axial heat conduction effects are negligible. Use the following di-

mensionless variables:

Show that the temperature profiles in this system are

in which Xi and

are the eigenfunctions and eigenvalues obtained from the solution to the

following equation:

with boundary conditions

finite at

0 and X

1. Show further that

(b)

Solve

Eq.

12D.2-3 for the Newtonian fluid by obtaining a power series solution for Xi. Cal-

culate the lowest eigenvalue by solving an algebraic equation. Check your result against that

given in Table 12D.2.

(c)

From the work involved in (b) in computing

it can be inferred that the computation

the higher eigenvalues is quite tedious. For eigenvalues higher than the second or third the

Wenzel-Kramers-Brillouin

(WKB) method" can be used; the higher the eigenvalue, the more

accurate the WKB method is. Read about this method, and verify that for the Newtonian fluid

similar formula has been derived for the power law model.''

Table

12D.2

Eigenvalues

for the Graetz-Nusselt Problem for Newtonian Fluidsa

By Stodola and

By direct calculationb By WKB methodVianello methodd

3.67

3.56

3.661"

2 22.30 22.22

56.95

56.88

107.6 107.55

The

here correspond to

in W.

Rohsenow,

Hartnett, and Y.

Cho,

Handbook of

Heat Transfer,

McGraw-Hill (New York), Table 5.3 on p. 510.

Values taken from

Yamagata,

Memoirs of the Faculty of Engineering,

Kyfishfi University,

Volume VIII, No.

Fukuoka, Japan (1940).

Computed from

Eq.

12D.2-5.

For the particular trial function in part (d) of the problem.

Heading,

An Introduction to Phase-Integral Methods,

Wiley, New York (1962);

Sellars,

Tribus, and

Klein,

Trans.

ASME,

78,44148 (1956).

"I.

Whiteman and W.

Drake,

Trans. ASME,

80,728-732 (1958).

Problems

405

(d)

Obtain the lowest eigenvalue by the method of Stodola and Vianello. Use Eqs. 71a and

72b on p. 203 of Hildebrand's book,'2 with

2(1

E2) for Newtonian flow and

as a simple, but suitable, trial function. Show that this leads quickly to the value

3.661.

12D.3.

The Graetz-Nusselt problem (asymptotic solution for large

2).

Note that, in the limit of very

large

only one term

1) is needed in Eq. 12D.2-2. It is desired to use this result to com-

pute the heat flux at the wall, qO, at large z and to express the result as

(a function of system and fluid properties)

(Tb

To)

(12D.3-1)

where

is the "bulk fluid temperature" defined in

Eq.

10.8-33.

(a) First verify that

Here

is the same as in Problem 12D.2, and

(T!,

To)/(Tl

To).

(b) Show that for large

Eq. 12D.3-2 and

Eq.

12D.2-2 both give

Hence for large z, all one needs to know is the first eigenvalue; the eigenfunctions need not be

calculated. This shows how useful the method of Stodola and Vianello12 is for computing the

limiting value of a heat flux.

12D.4.

The Graetz-Nusselt problem (asymptotic solution for small

2).

(a) Apply the method of Example 12.2-2 to the solution of the problem discussed in Problem

12D.2. Consider a Newtonian fluid and use the following dimensionless quantities:

Show that the method of combination of variables gives

in which

(AJcT~/~~)'/~.

(b)

Show that the wall flux is

The quantity (Re Pr D/z)

(4/m-)(wtp/kz) appears frequently; the grouping

(wi',/kz) is

called the Graetz number. Compare this result with that in Eq. 12D.3-3, with regard to the

de-

pendence on the dimensionless groups.

(c)

How may the results be written so that they are valid for any generalized Newtonian

model?

12D.5.

The Graetz problem for flow between parallel plates. Work through Problems 12D.2,3, and

for flow between parallel plates (or flow in a thin rectangular duct).

12D.6.

The constant wall heat flux problem for parallel plates. Apply the methods used in §10.8,

Example

12.2-1,

and

Ex.

12.2-2 to the flow between parallel plates.

Hildebrand,

Advanced Calculus

for

Applications,

Prentice-Hall, Englewood

Cliffs,

N.J.

(19631,

55.5.

406

Chapter

Temperature Distributions with More Than One Independent Variable

12D.7.

Asymptotic solution for small

for laminar tube flow with constant heat

flux.

Fill in the

missing steps between

Eq.

12.2-23

and

Eq.

12.2-24.

Insertion of the expression for

into

Eq.

12.2-23

gives

Why do we introduce the symbols

and

Next, exchange the order of integration to get

Then perform the integration over and obtain

Then use the definitions T(a)

J,"

t"-'ecfdt

and r(a,

J,"

t"-'ectdt

for the complete and in-

complete gamma functions.

12D.8.

Forced conduction heat transfer from a flat plate (thermal boundary layer extends beyond

the momentum boundary layer). Show that the result analogous

Eq.

12.4-14

for

isI3

Schlichting,

Boundary-Layer Theory,

7th edition,

McGraw-Hill,

New

York

(19791,

306.