Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

Chapter

Temperature Distributions

in Turbulent Flow

913.1

Time-smoothed equations of change for incompressible nonisothermal flow

913.2

The time-smoothed temperature profile near a wall

513.3

Empirical expressions for the turbulent heat Aux

913.4~

Temperature distribution for turbulent flow in tubes

913.5~

Temperature distribution for turbulent flow in jets

g13.6'

Fourier analysis of energy transport in tube flow at large Prandtl numbers

In Chapters

we have shown how to obtain temperature distributions in solids

and in fluids in laminar motion. The procedure has involved solving the equations of

change with appropriate boundary and initial conditions.

We now turn to the problem of finding temperature profiles in turbulent flow. This

discussion is quite similar to that given in Chapter

We begin by time-smoothing the

equations of change. In the time-smoothed energy equation there appears a turbulent

heat flux

q(t),

which is expressed in terms of the correlation of velocity and temperature

fluctuations. There are several rather useful empiricisms for

ij't',

which enable one to pre-

dict time-smoothed temperature distributions in wall turbulence and in free turbulence.

We use heat transfer in tube flow to illustrate the method.

The most apparent influence of turbulence on heat transport is the enhanced trans-

port perpendicular to the main flow. If heat is injected into a fluid flowing in

laminar

flow in the

direction, then the movement of heat in the

and

directions is solely

conduction and proceeds very slowly. On the other hand, if the flow is turbulent, the heat

"spreads out" in the

and

directions extremely rapidly. This rapid dispersion of heat is

a characteristic feature of turbulent flow. This mixing process is worked out in some de-

tail here for flow in tubes and in circular jets.

Although it has been conventional to study turbulent heat transport via the time-

smoothed energy equation, it is also possible to analyze the heat flux at a wall by use of a

Fourier transform technique without time-smoothing. This is set forth in the last section.

513.1

TIME-SMOOTHED EQUATIONS OF CHANGE FOR

INCOMPRESSIBLE NONISOTHERMAL FLOW

s5.2

we introduced the notions of time-smoothed quantities and turbulent fluctua-

tions. In this chapter we shall be primarily concerned with the temperature profiles. We

introduce the time-smoothed temperature

and temperature fluctuation T', and write

analogously to Eq.

5.2-1

T=T+T' (13.1-1)

408

Chapter

Temperature Distributions in Turbulent Flow

Clearly T' averages to zero so that

but quantities like v:T', viT', and

will not

be zero because of the "correlation" between the velocity and temperature fluctuations

at any point.

For a nonisothermal pure fluid we need three equations of change, and we want

discuss here their time-smoothed forms. The time-smoothed equations of continuity and

motion for a fluid with constant density and viscosity were given in Eqs. 5.2-10 and

12,

and need not be repeated here. For a fluid with constant p, p,

and

Eq. 11.2-5, when

put in the

d/dt

form by using Eq. 3.5-4, and with Newton's and Fourier's law included,

becomes

in which only a few sample terms in the viscous dissipation term -(T:VV)

p@,

have

been written (see Eq. B.7-1 for the complete expression).

In Eq. 13.1-2 we replace

T', v, by

v:, and so on. Then the equation

is time-smoothed to give

Comparison of this equation with the preceding one shows that the time-smoothed

equation has the same form as the original equation, except for the appearance of the

terms indicated by dashed underlines, which are concerned with the turbulent fluctua-

tions.

are thus led to the definition of the turbulent heat flux

q"'

with components

A-

(t)

v'~f

(t)

v'~f

(t)

v'~'

-P

(13.1-4)

and the turbulent energy dissipation function

8:):

The similarity between the components of

q")

in Eq. 13.1-4 and those of ?"' in Eq. 5.2-8

should be noted. In Eq. 13.1-5, v,',

vi,

and

are synonymous with v:, v;, and vi, and

x,,

x2, and

have the same meaning as

and

To summarize, we list all three time-smoothed equations of change for turbulent

flows of pure fluids with constant p,

and

in their

D/Dt

form (the first two were

given in Eqs. 5.2-10 and 12):

Continuity

0 (13.1-6)

Motion

-vp

(5'"'

?"')I

(13.1-7)

Energy

513.2

The Time-Smoothed Temperature Profile Near a Wall

409

in which it is understood that

D/Dt

d/dt

Here

q'"'

k~?,

and

is the vis-

cous dissipation function of Eq. B.7-1, but with all the vi replaced by

In discussing turbulent heat flow problems, it has been customary to drop the vis-

cous dissipation terms. Then, one sets up a turbulent heat transfer problem as for lami-

nar flow, except that

and

are replaced by

?'")

l@'

and

q'"'

q(",

respectively, and

time-smoothed

and

are used in the remaining terms.

913.2

THE TIME-SMOOTHED TEMPERATURE

PROFILE

NEAR

WALL'

Before giving empiricisms for

q("

in the next section, we present a short discussion of

some results that do not depend on any empiricism.

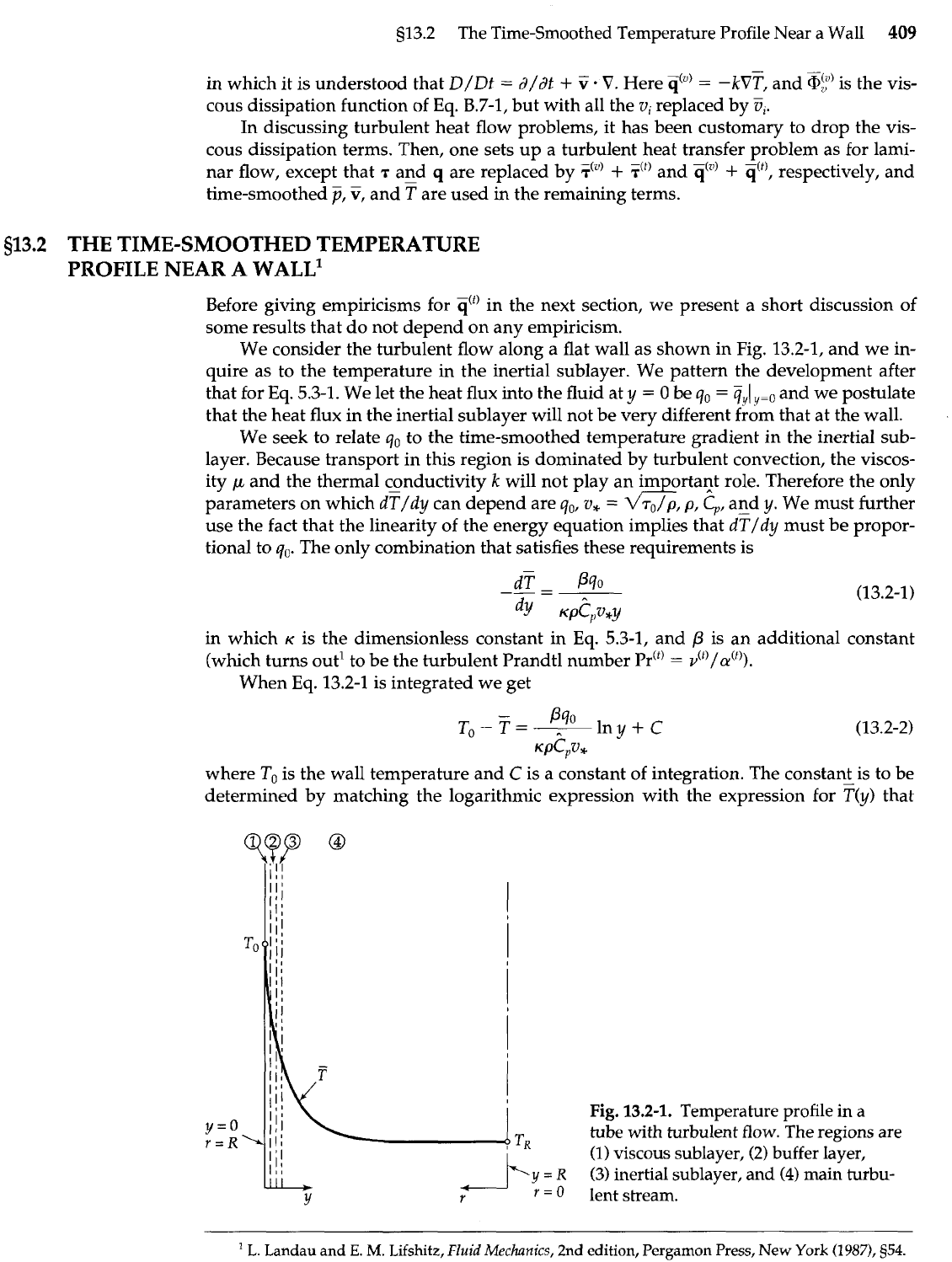
We consider the turbulent flow along a flat wall as shown in Fig. 13.2-1, and we in-

quire as to the temperature in the inertial sublayer. We pattern the development after

that for Eq. 5.3-1. We let the heat flux into the fluid at

G(y=O

and we postulate

that the heat flux in the inertial sublayer will not be very different from that at the wall.

We seek to relate

to the time-smoothed temperature gradient in the inertial sub-

layer. Because transport in this region is dominated by turbulent convection, the viscos-

ity

and the thermal conductivity

will not play an im orta$ role. Therefore the only

parameters on which dT/dy can depend are

qo,

%/p,

C,,

and

We must further

use the fact that the linearity of the energy equation implies that dT/dy must be propor-

tional to

qo.

The only combination that satisfies these requirements is

in which

is the dimensionless constant in

Eq.

5.3-1, and

is an additional constant

(which turns out1 to be the turbulent Prandtl number ~r"'

~'~)/cu(')).

When Eq. 13.2-1 is integrated we get

Pqo

To-T=,-lny+C

KPC~.U,

where To is the wall temperature and C is a constant of integration. The constant is to be

determined by matching the logarithmic expression with the expression for

T(y)

that

Fig.

13.2-1.

Temperature profile in a

tube with turbulent

flow.

The regions are

+-k

(1)

viscous sublayer,

(2)

buffer layer,

(3)

inertial sublayer, and

(4)

main turbu-

lent stream.

L. Landau and

Lifshitz,

Fluid

Mechanics,

2nd

edition, Pergamon Press,

New

York

(1987),

554.

410

Chapter

Temperature Distributions in Turbulent Flow

holds at the junction with the viscous sublayer. The latter expression will involve both

and

hence

will n~cessarily contain

and

and will therefore include the dimen-

sionless group Pr

C,p/k. If, in addition, we introduce the dimensionless coordinate

yv,/u, then Eq. 13.2-2 can be rewritten as

YV*

for,

in which f(Pr) is a function representing the thermal resistance between the wall and the

inertial sublayer. Landau and Lifshitz (see Ref. 1 on page

409)

estimate, from a mixing-

length argument (see Eq. 13.3-3), that, for large Prandtl numbers, f(Pr)

constant

~3~'';

however, Example 13.3-1 implies that the function f(Pr)

constant ~r'/"s better. Keep

in mind that Eq. 13.2-3 can be expected to be valid only in the inertial sublayer and that

should not be used in the immediate neighborhood of the wall.

s13.3

EMPIRICAL EXPRESSIONS FOR THE TURBULENT HEAT

FLUX

In g13.1 we saw that the time-smoothing of the energy equation gives rise to a turbulent

heat flux q't'. In order to solve the energy equation for the time-smoothed temperature

profiles, it is customary to postulate a relation between

q'"

and the time-smoothed tem-

perature gradient. We summarize here two of the most popular empirical expressions;

more of these can be found in the heat transfer literature.

Eddy Thermal Conductivity

By analogy with the Fourier law of heat conduction we may write

in which the quantity

k't'

is called the turbulent therrnal conductivity or the eddy thennal

conductivity. This quantity is not a physical property of the fluid, but depends on posi-

tion, direction, and the nature of the turbulent flow.

The eddy kinematic viscosity

df'

p't'/p

and the eddy thermal diffusivity

a"'

k'"/pCP have the same dimensions. Their ratio is a dimensionless group

called the turbulent

Pvandtl

number. This dimensionless quantity is of the order of unity,

values in the literature varying from 0.5 to 1 .O. For gas flow in conduits, ranges from

0.7

to 0.9 (for circular tubes the value 0.85 has been recommended1), whereas for flow in

jets and wakes the value is more nearly 0.5. The assumption that

~r"'

1 is called the

Reynolds analogy.

The

Mixing-Length Expression of

Prandtl and Taylor

According to Prandtl's mixing-length theory, momentum and energy are transferred in

turbulent flow by the same mechanism. Hence, by analogy with

Eq.

5.4-4, one obtains

Kays

and

Crawford,

Convective

Heat

arid

Mass

Tvunsfer,

3rd

edition,

McGraw-Hill,

New York (1993),

pp.

259-266.

913.4 Temperature Distribution for Turbulent Flow in Tubes

411

where

is the Prandtl mixing length introduced in

Eq.

5.4-4.

Note that this expression

predicts that ~r'"

The Taylor vorticity transport theory2 gives ~r"'

Use the Reynolds analogy

(df'

a"'), along with

Eq.

5.4-2 for the eddy viscosity, to estimate

the wall heat flux

for the turbulent flow in a tube of diameter

2R.

Express the result in

Approximate

terms of the temperature-difference driving force

TR,

where

is the temperature at

Relation for the Wall

the wall (y

and

is the time-smoothed temperature at the tube axis (y

R).

Heat Flux

for

Turbulent

Flow in a Tube

SOLUTION

The time-smoothed radial heat flux

a tube is given by the sum of

IfZ")

and

4;':

Here we have used

Eq.

13.3-1 and the Reynolds analogy, and we have switched to the coordi-

nate y, which is the distance from the wall. We now use the empirical expression of

Eq.

5.4-2,

which applies across the viscous sublayer next to the wall:

where

ijr

-i$

has been used.

If now we approximate the heat flux

Eq.

13.3-5

by its wall value

qo,

then integration

from

to y

gives

For very large Prandtl numbers, the upper limit

in the integral can be replaced by

since

the integrand is decreasing rapidly with increasing y. Then when the integration on the left

side is performed and the result is put into dimensionless form, we get

in which

Eq.

6.1-4a has been used to eliminate

in favor of the friction factor.

The above development is only approximate. We have not taken into account the change

of the bulk temperature as the fluid moves axially through the tube, nor have we taken into

account the change in the heat flux throughout the tube. Furthermore, the result is restricted

to very high Pr, because of the extension of the integration to y

Another derivation is

given

the next section, which

free from these assumptions. However, we will see that at

large Prandtl numbers the result in

Eq.

13.4-20 simplifies to that in

Eq.

13.3-7

but with a differ-

ent numerical constant.

513.4

TEMPERATURE DISTRIBUTION FOR

TURBULENT FLOW IN TUBES

510.8

we showed how to get the asymptotic behavior of the temperature profiles for

large

in a fluid in laminar flow in a circular tube. We repeat that problem here, but for a

fluid in fully developed turbulent flow. The fluid enters the tube of radius

at an inlet

temperature

T,.

For

the fluid is heated because of

uniform radial heat flux

the wall

(see

Fig. 13.4-1).

Taylor,

Proc.

Roy.

Soc. (London),

A135,685-702

(1932);

Phil.

Trans.,

A215,l-26

(1915).

412

Chapter

Temperature Distributions in Turbulent Flow

Fluid at temperature

in fully

developed turbulent flow

Electrical heating coil to provide

z=O

constant wall

flux

Fig.

13.4-1.

System used for heating a liquid in fully developed

turbulent flow with constant heat flux for

We start from the energy equation, Eq. 13.1-8, written in cylindrical coordinates

Then insertion of the expression for the radial heat flux from Eq. 13.3-4 gives

This is to be solved with the boundary conditions

B.C. 1: at r

0, T

finite

B.C.

at r

(a constant)

B.C.

atz=O, T=Tl (13.4-5)

We now use the same dimensionless variables as already given in Eqs. 10.8-16 to 18

(with

in place of T in the definition of the dimensionless temperature). Then Eq. 13.4-2

in dimensionless form is

in which +(,$I

EZ/v,,, is the dimensionless turbulent velocity profile. This equation is

to be solved with the dimensionless boundary conditions

B.C. 1: at

finite (13.4-7)

B.C. 2:

at[=l, +-=I

(13.4-8)

BS.

3: atC=O, 0=0 (13.4-9)

The complete solution to this problem has been given,' but we content ourselves here

with the solution for large

We begin by assuming an asymptotic solution of the form

Eq. 10.8-23

which must satisfy the differential equation, together with B.C.

and

and Condition

Eq. 10.8-24 (with T and

vmax(l

replaced by

and v,

urn,,+(()).

The result-

ing equation for

!!!

Notter and

Sleicher,

Chem.

Eng.

Sci.,

27,2073-2093

(1972).

513.4 Temperature Distribution for Turbulent How in Tubes

413

Integrating this equation twice and then constructing the function

using Eq. 13.4-10,

we get

o=c~+c~/

(13.4-12)

Z[I

(L~(~)/~)I

4[1

(a't)/a)~

in which it is understood that

a"'

is a function of

and

is shorthand for the integral

The constant of integration

is set equal to zero in order to satisfy

B.C.

1. The constant

is found by applying

B.C.

which gives

The remaining constant, C2, can, if desired, be obtained from Condition 4, but we shall

not need it here (see Problem 13D.1).

We next get an expression for the dimensionless temperature difference

Ob, the

"driving force" for the heat transfer at the tube wall:

In the second line, the order of integration of the double integral has been reversed.

The inner integral in the second term on the right is just

10)

I@,

and the portion

containing

I(1)

exactly cancels the first term in Eq. 13.4-15. Hence when Eq. 13.4-14 is

used, we get

But the quantity I(1) appearing in

Eq.

13.4-16 has a simple interpretation:

Finally, we want to get the dimensionless wall heat flux,

the reciprocal of which is2

To use this result, it is necessary to have an expression for the time-smoothed velocity

distribution (which appears in

I([)),

the turbulent kinematic viscosity

v"'

as a function

of position, and a postulate for the turbulent Prandtl number Pr"'.

Equation

13.4-19

was first developed by

Lyon,

Chem.

Eng.

Prog.,

47,

75-79 (1950) in a

paper

liquid-metal heat transfer. The left side of

Eq.

13.4-19 is the reciprocal of the Nusselt

number, Nu

hD/k,

which is a dimensionless heat transfer coefficient. This nomenclature is

discussed in the next chapter.

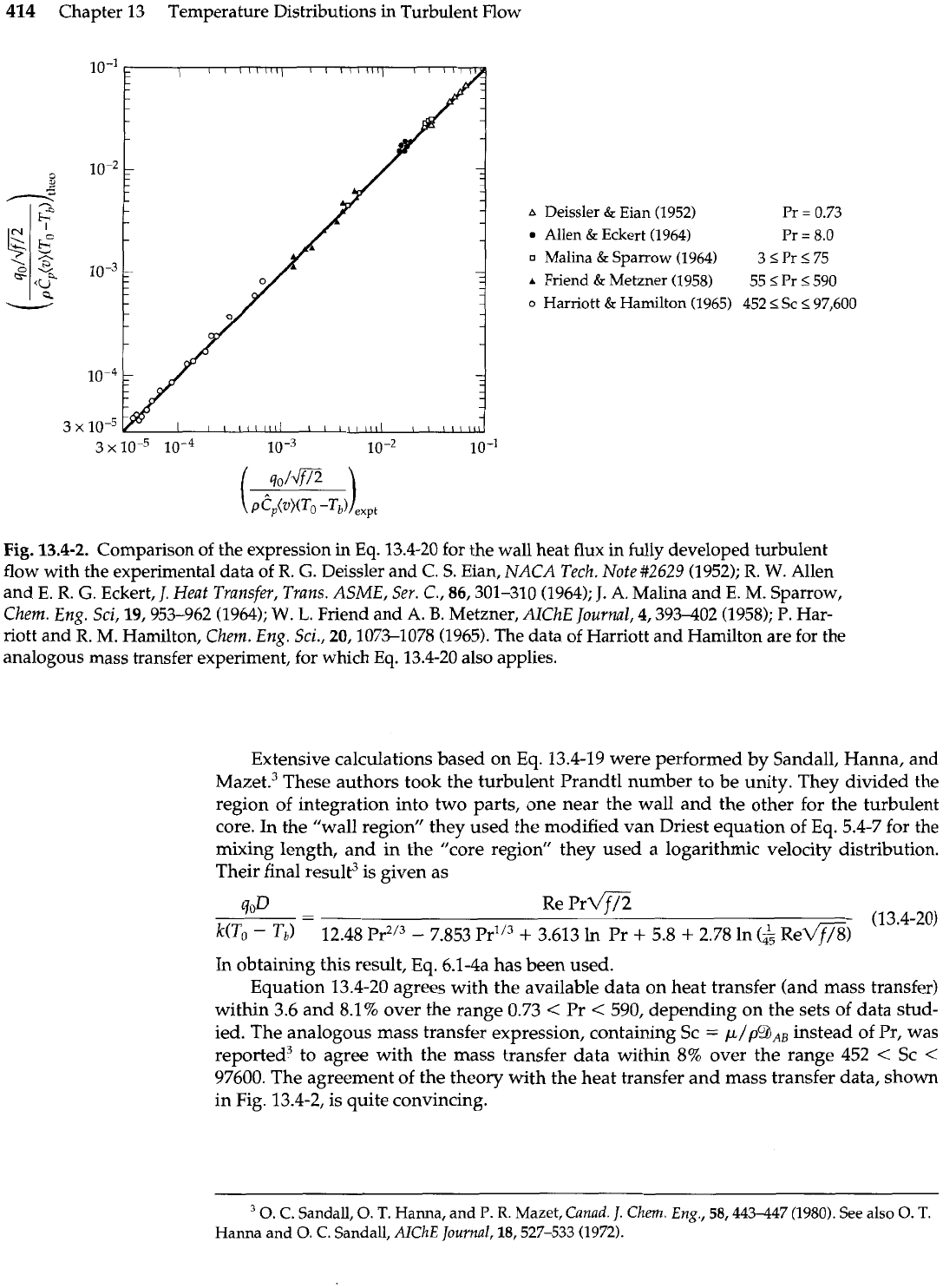
414

Chapter 13 Temperature Distributions in Turbulent Flow

Deissler

Eian (1952)

Allen

Eckert (1964)

Malina

Sparrow (1964)

Friend

Metzner (1958)

Harriott

Hamilton (1965)

Fig.

13.4-2. Comparison of the expression in

Eq.

13.4-20 for the wall heat flux in fully developed turbulent

flow with the experimental data of

Deissler and

Eian, NACA

Tech. Note

#2629

(1952);

Allen

and

Eckert,

Heat Transfer,

Trans.

ASME,

Ser.

C., 86,301-310 (1964);

Malina and

M. Sparrow,

Chem.

Eng.

Sci, 19,953-962 (1964);

Friend and

Metzner, AlChE

Journal,

4,393402 (1958);

Har-

riott and

Hamilton,

Chem.

Eng.

Sci., 20,1073-1078 (1965). The data of Harriott and Hamilton are for the

analogous mass transfer experiment, for which

Eq.

13.4-20 also applies.

Extensive calculations based on

Eq.

13.4-19 were performed by Sandall, Hanna, and

~azet.~ These authors took the turbulent Prandtl number to be unity. They divided the

region of integration into two parts, one near the wall and the other for the turbulent

core. In the "wall region" they used the modified van Driest equation of

Eq.

5.4-7 for the

mixing length, and in the "core region" they used

logarithmic velocity distribution.

Their final result3 is given as

In obtaining this result,

Eq.

6.1-4a has been used.

Equation 13.4-20 agrees with the available data on heat transfer (and mass transfer)

within 3.6 and 8.1% over the range 0.73

590, depending on the sets of data stud-

ied. The analogous mass transfer expression, containing Sc

p/p%,,

instead of Pr,

was

reported3 to agree with the mass transfer data within 8% over the range 452

97600. The agreement

the theory with the heat transfer and mass transfer data, shown

in Fig. 13.4-2, is quite convincing.

Sandall,

Hanna, and

Mazet,

Canad.

Chem. Eng.,

58,443-447 (1980). See also

Hanna and

Sandall,

AIChE Jouvnal,

18,527-533 (1972).

913.5 Temperature Distribution for Turbulent Flow in Jets

415

513.5

TEMPERATURE DISTRIBUTION FOR

TURBULENT FLOW IN JETS'

In 55.6 we derived an expression for the velocity distribution in a circular fluid jet dis-

charging into an infinite expanse of the same fluid (see Fig. 5.6-1). Here we wish to ex-

tend this problem by considering an incoming jet with temperature

higher than that

of the surrounding fluid

TI.

The problem then is to find the time-smoothed temperature

distribution T(r, z) in a steadily driven jet. We expect that this distribution will be monot-

one decreasing in both the r and z directions.

We start by assuming that viscous dissipation is negligible, and we neglect the con-

tribution

$"'

to the heat flux as well as the axial contribution to

q"'.

Then Eq. 13.1-8 takes

the time-averaged form

Then we express the turbulent heat flux in terms of the turbulent thermal conductivity

introduced in Eq. 13.3-1:

When

Eq.

13.5-1 is written in terms of a dimensionless temperature function

it becomes

Here it has been assumed that the turbulent Prandtl number and the turbulent kinematic

viscosity are constants (see the discussion after Eq. 5.6-3). This equation

to be solved

with the boundary conditions:

B.C.

atz=O, @=1

at r

is finite

atr=m,

O=O

Next we introduce the expressions for the time-smoothed velocity components

and

in terms of a stream function F([), as given in Eqs. 5.6-12 and 13, and a trial expression

for the dimensionless time-smoothed temperature function:

Here

r/z and

(pv't'/w)z, where

is the total mass flow rate in the jet. The pro-

posal in Eq. 13.5-8 is motivated by the expression for

that was found in Eq. 5.6-21.

When these expressions for the velocity components and the dimensionless temper-

ature are substituted into

Eq.

13.5-1, some terms cancel and others can be combined, and

as a result, the following rather simple equation is obtained:

Hinze,

Turbulence,

2nd

edition,

McGraw-Hill, New

York

(1975),

pp.

531-546.

416

Chapter

Temperature Distributions in Turbulent Flow

This equation can be integrated once to give

The constant of integration may be set equal to zero, since,

second integration from

then gives

according to

Finally, comparison of Eqs. 13.5-12 and 13.5-8 with Eq. 5.6-21 shows that the shapes of

the time-smoothed temperature and axial velocity profiles are closely related,

an equation attributed to Reichardt.' This theory provides a moderately satisfactory ex-

planation for the shapes of the temperature profiles.' The turbulent Prandtl (or Schmidt)

number deduced from temperature (or concentration) measurements in circular jets is

about 0.7.

The quantity

appearing in Eq. 13.5-12 was given explicitly in Eq. 5.6-23 as

wm(1

/dt)),

where

is the rate of momentum flow in the jet, defined in Eq.

5.6-

2. Similarly, an expression for the quantity f(0) in Eq. 13.5-12 can be found by equating

the energy in the incoming jet to the energy crossing any plane downstream:

Insertion of the expressions for the velocity and temperature profiles and integrating

then gives

Combining Eqs. 13.5-3, 13.5-8,5.6-23, 13.5-12, and 13.5-15 then gives the complete expres-

sion for the temperature profiles T(r,

in the circular turbulent jet, in terms of the total

momentum of the jet, the turbulent viscosity, the turbulent Prandtl number, and the

fluid density.

13.6

FOURIER ANALYSIS

ENERGY TRANSPORT IN

TUBE FLOW

LARGE PRANDTL NUMBERS

In the preceding two sections we analyzed energy transport in turbulent systems by

use

of time-smoothed equations of change. Empirical expressions were then required to

de-

scribe the turbulent fluxes in terms of time-smoothed profiles, using eddy transport coef-

Reichardt,

Zeits.

angew.

Math.

Mech.,

24,268-272

(1944).