Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

s13.6

Fourier Analysis of Energy Transport

Tube Flow at Large Prandtl Numbers

417

ficients estimated from experiments. In this section we analyze a turbulent energy trans-

port problem without time-smoothing-that is, by direct use of the energy equation with

fluctuating velocity and temperature fields. The Fourier transform1 is well suited for

such problems, and the "method of dominant balanceu2 gives useful information with-

out detailed computations.

The specific question considered here is the influence of the thermal diffusivity,

k/&,

on the expected distribution and fluctuations of the fluid temperature in turbulent

forced convection near a wall.3 This topic was discussed in Example 13.3-1 by an approx-

imate procedure.

Let us consider a fluid with constant

and

in turbulent flow through a tube of

inner radius

;D.

The flow enters at

with uniform temperature

and exits at

The tube wall is adiabatic for

0, and isothermal at

for 0

Heat con-

duction in the

direction is neglected. The temperature distribution T(r, 8,

is to be

analyzed in the long-time limit, in the thin thermal boundary layer that forms for

when the

molecular

thermal diffusivity

is small (as in a Newtonian fluid when the

Prandtl number, Pr

Spp/k

p/pa, is large).

stretching function

~(a)

will be derived

for the average thickness of the thermal boundary layer without introducing an eddy

thermal diffusivity

df'.

In the limit as

0, the thermal boundary layer lies entirely within the viscous sub-

layer, where the velocity components are given by truncated Taylor expansions in the

distance

r from the wall (compare these expansions with those in Eqs.

5.4-8

to 10)

Here the coefficients

and

are treated as given functions of 8, z, and

These velocity

expressions satisfy the no-slip conditions and the wall-impermeability condition at

and the continuity equation at small

and are consistent with the equation of motion to

the indicated orders in

The energy equation can then be written as

with the usual boundary layer approximation for

VZT,

and with the following boundary

conditions on T(y,

t):

Inlet condition:

T(y, 8,0,

T, for 0

3.6-5)

Wall condition:

T(0,

for 0

(13.6-6)

The initial temperature distribution T(y,

0) is not needed, since its effect disappears

in the long-time limit.

To obtain results asymptotically valid for

0, we introduce a stretched coordi-

nate

y/~(cu), which is the distance from the wall relative to the average boundary

layer thickness ~(a). The range of

is from 0 at

0 to

at y

in the limit as

Bracewell,

The Fourier Transform and its Applications,

2nd edition, McGraw-Hill, New York

(1978).

This method

well presented in

Bender and S.

A. Orzag,

Advanced Mathematical Methods for

Scientists and Engineers,

McGraw-Hill, New York

(1978),

pp.

435437.

Stewart,

AIChE

Journal,

33,2008-2016 (1987);

errata,

ibid.,

34,

1030 (1988);

Stewart and

O'Sullivan,

AKhE Journal

(to be submitted).

418

Chapter

Temperature Distributions

Turbulent Flow

Use of

in place of y, and introduction of the dimensionless temperature function O(Y,

0, z, t)

T,)/(To

TI),

enable us to rewrite Eq. 13.6-4 as

with boundary conditions as follows:

Inlet condition: at

O(Y, 0,0, t)

0 for

(13.6-8)

Wall condition: at

W0, 8, z, t)

for 0

(13.6-9)

Equation 13.6-7 contains an unbounded derivative d@/dt with a coefficient

indepen-

dent of

Thus a change of variables is needed to analyze the influence of the parameter

in this problem. For this purpose we turn to the Fourier transform, a standard tool for

analyzing noisy processes.

We choose the following definition1 for the Fourier transform of a function g(t) into

the domain of frequency

particular position Y,

The corresponding transforms for the t-derivative and for products of functions of

are

and the latter integral is known as the convolution of the transforms and

Before taking the Fourier transforms of Eqs. 13.6-7 to

we express each included

function g(t) as a time average

plus a fluctuating function gf(t) and expand each prod-

uct of such functions. The resulting expressions have the following Fourier transforms:

Here 6(v) is the Dirac delta function, obtained as the Fourier transform of the function

g(t)

1 in the long-duration limit. The leading term in the last line is a real-valued im-

pulse at

0, coming from the time-independent product

The next two terms are

complex-valued functions of the frequency

The convolution term

may contain

complex-valued functions of v, along with a real-valued impulse

~(v)g'h'

coming from

time-independent products of simple harmonic oscillations present in

and

h'.

Taking the Fourier transform of Eq. 13.6-7 by the method just given and noting that

dG/dt is identically zero, we obtain the differential equation

513.6

Fourier Analysis of Energy Transport in Tube Flow at Large Prandtl Numbers

419

for the Fourier-transformed temperature

6(~,

0, z, v). The transformed boundary condi-

tions are

Inlet condition:

at z

O(Y,

0, z,

for

(13.6-16)

Wall

condition:

O(Y,

S(v)

for

(13.6-17)

Here again, the unit impulse function 6(v) appears as the Fourier transform of the func-

tion

g(t)

1 in the long-duration limit.

Two types of contributions appear in Eq. 13.6-15: real-valued zero-frequency im-

pulses S(v) from functions and products independent of t, and complex-valued functions

from time-dependent product terms. We consider these two types of contributions

separately here, thus decoupling Eq. 13.6-15 into two equations.

We begin with the zero-frequency impulse terms. In addition to the explicit 6(v)

terms of Eq. 13.6-15, implicit impulses arise in the convolution terms from synchronous

oscillations

A-

of velocity and temperature, giving rise to the turbulent energy flux

pC,v'T1

discussed in s13.2. The coefficients of all the impulse terms must be proportional

functions of

in order that the dominant terms at each point remain balanced (i.e., of

comparable size) as

0. Therefore, the coefficient

of the convective impulse terms,

including those from synchronous fluctuations, must be proportional to the coefficient

a/K2

of the conductive impulse term, giving

for the dependence of the average thermal boundary layer thickness on the Prandtl number.

The remaining terms in Eq. 13.6-15 describe the turbulent temperature fluctuations.

They include the accumulation term 2n-iv6' and the remaining convection and conduc-

tion terms. The coefficients of all these terms (including 271-i~ in the leading term) must

be proportional functions of

in order that these terms likewise remain balanced as

0. This reasoning confirms Eq. 13.6-18 and gives the further relation

for the frequency bandwidth

of the temperature fluctuations. Consequently, the

stretched frequency Pr1'3v and stretched time ~r-"~t are natural variables for reporting

Fourier analyses of turbulent forced convection. Shaw and Hanratty4 reported turbu-

lence spectra for their mass transfer experiments analogously, in terms of a stretched fre-

quency variable proportional to sc1I3

(here Sc

p/p9AB

is the Schmidt number, the

mass transfer analog of the Prandtl number, which contains the binary diffusivity

9AR,

be introduced in Chapter 16).

Thus far we have considered only the leading term of a Taylor expansion in

for

each term in the energy equations. More accurate results are obtainable by continuing

the Taylor expansions to higher powers of

and thus of Pr-'13D. The resulting formal

solution is a perturbation expansion

for the distribution of the fluctuating temperature over position and frequency in a given

velocity field.

The expansion for

(the long-time average of the temperature) corresponding to Eq.

13.6-20 is obtained from the zero-frequency part of

@,(Y, 8,~)

K~,(Y,

8,Z)

(13.6-21)

D. A.

Shaw

and

Hanratty,

AIChE

Journal,

23,160-169 (1977);

Shaw

and

Hanratty,

NChE

Journal,

23,28--37 (1977).

420

Chapter 13 Temperature Distributions in Turbulent Flow

From this we can calculate the local time-averaged heat flux at the wall:

and the local Nusselt number is then

Then the mean Nusselt number over the wall surface for heat transfer, and the analo-

gous quantity for mass transfer, are

In this last equation Sh,,

O,,

and Sc are the mass transfer analogs of Nu,,

and Pr.

give the mass transfer expression here (rather than wait until Part 111) because electrochem-

ical mass transfer experiments give better precision than heat transfer experiments and the

available range of Schmidt numbers is much greater than that of Prandtl numbers.

If the expansions in

Eq.

13.6-24 and 25 are truncated to one term,

are led to

Nu,

and Sh,

SC~'~. These expressions are essential ingredients in the famous

Chilton-Colburn relations5 (see Eqs. 14.3-18 and 19, and Eqs. 22.3-22 to 24). The first term

Eq.

13.6-24 or 25 also corresponds to the high Prandtl (or Schmidt) number asymptote

of Eq. 13.4-20.6

With the development of electrochemical methods of measuring mass transfer at

surfaces, it has become possible to investigate the second term in Eq. 13.6-25. In

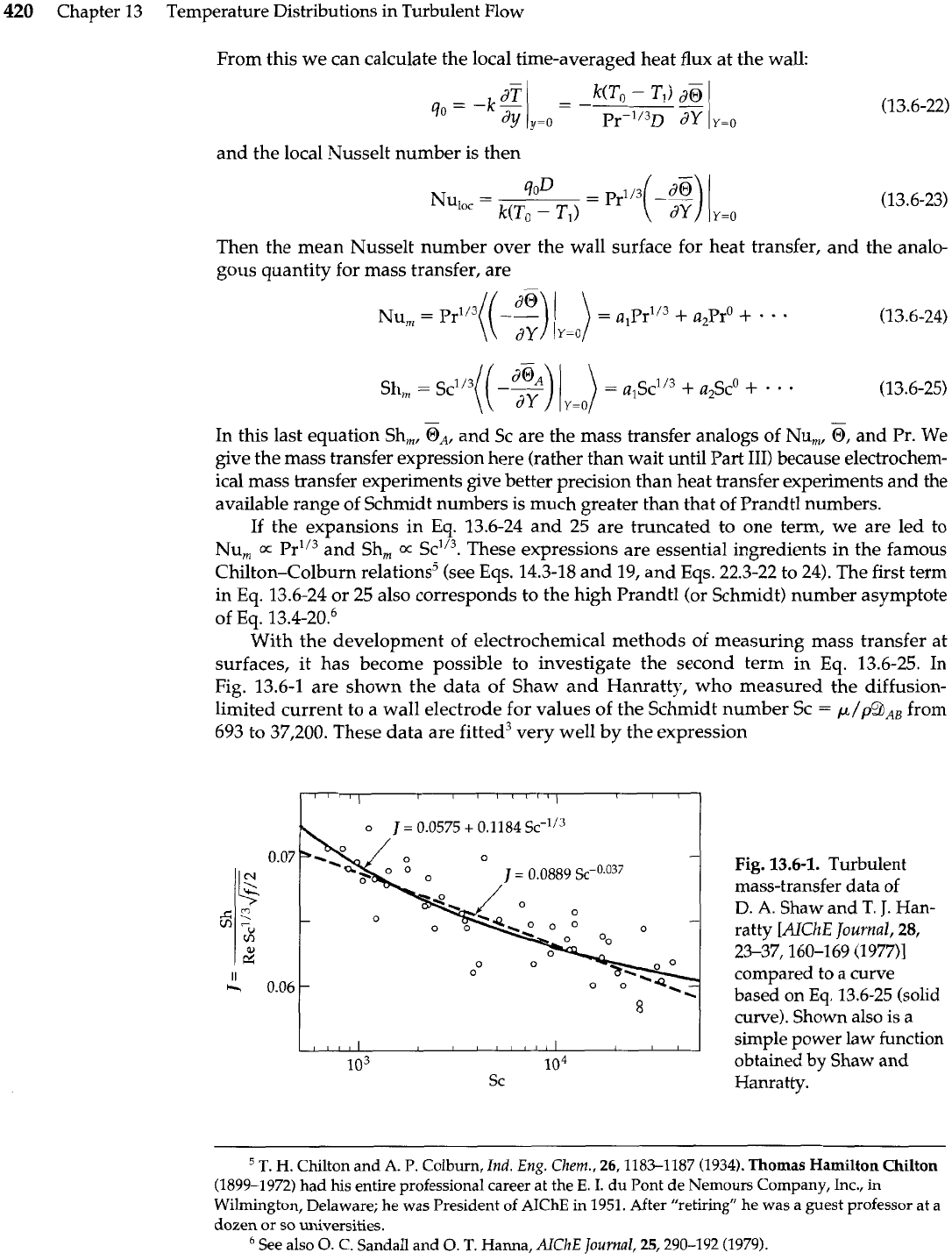
Fig. 13.6-1 are shown the data of Shaw and Hanratty, who measured the diffusion-

limited current to a wall electrode for values of the Schmidt number Sc

p/p9,,

from

693 to 37,200. These data are fitted3 very well by the expression

Fig.

13.6-1.

Turbulent

mass-transfer data of

Shaw and T.

Han-

ratty

[AlChE

Journal,

28,

23-37,160-169 (1977)I

compared to a curve

based on

Eq.

13.6-25 (solid

curve). Shown also is a

simple power law function

obtained by Shaw and

Hanratty.

Chilton and A. P. Colburn,

Ind.

Eng.

Chem.,

26,1183-1187 (1934).

Thomas Hamilton

Chilton

(1899-1972) had his entire professional career at the

du Pont de Nemours Company, Inc., in

Wilmington, Delaware; he was President of AIChE in 1951. After "retiring" he was a guest professor at a

dozen or so universities.

See also

C. Sandall and

Hanna,

AIChE

Journal,

25,290-192 (1979).

Problems

421

in which f(Re) is the friction factor defined in Chapter 6. Equation 13.6-26 combines the

observed Re number dependence of the Sherwood number with the two leading terms

of Eq. 13.6-25 (that is, the coefficients a,, a,,

. .

are proportional to

em).

Equation

13.6-26 lends itself to clear physical interpretation: The leading term corresponds to a

diffusional boundary layer so thin that the tangential velocity is linear in

and the wall

curvature can be neglected, whereas the second term accounts for wall curvature and the

terms in the tangential velocity expansions of Eqs. 13.6-1 and 2). In higher approxima-

tions, special terms can be expected to arise from edge effects as noted by ~ewrnan~ and

Stewart

QUESTIONS FOR DISCUSSION

Compare turbulent thermal conductivity and turbulent viscosity as to definition, order of

magnitude, and dependence on physical properties and the nature of the flow.

What is the "Reynolds analogy," and what is its significance?

Is there any connection between Eq. 13.2-3 and Eq. 13.4-12, after the integration constants in

the latter have been evaluated?

Is the analogy between Fourier's law of heat conduction and

Eq.

13.3-1 a valid one?

What is the physical significance of the fact that the turbulent Prandtl number is of the order

of unity?

PROBLEMS

13B.1. Wall heat flux for turbulent flow in tubes (ap-

proximate). Work through Example 13.3-1, and fill in the

missing steps.

particular, verify the integration in going

from

Eq. 13.3-6 to Eq. 13.3-7.

13B.2. Wall heat flux for turbulent flow

tubes.

(a)

Summarize the assumptions in 513.4.

(b)

Work through the mathematical details of that section,

taking particular care with the steps connecting Eq. 13.4-12

and Eq. 13.4-16.

(c)

When is it not necessary to find the constant C, in Eq.

13.4-12?

13C.1. Wall heat

flux

for turbulent flow between two

parallel plates.

(a)

Work through the development in g13.4, and then per-

form

a similar derivation for turbulent flow in a thin slit

shown in Fig. 2B.3. Show that the analog of Eq. 13.4-19 is

in which

[

x/B

and

J(0

+([Id[.

(b) Show how the result in (a) simplifies for laminar flow

of Newtonian fluids, and for "plug flow" (flat velocity pro-

files).

Answer:

(b)

13D.1.

The temperature profile for turbulent flow

tubes.

calculate the temperature distribution for turbu-

lent flow in circular tubes from Eq. 13.4-12, it is necessary

to know C,.

(a)

Show how to get C2 by applying

B.C.

as was done in

510.8. The result is

(b) Verify that Eq. 13D.1-1 gives C,

for a Newtonian

fluid.

Newman,

Electroanalytical

Chemistry,

187-352 (1973).

Chapter

Interphase Transport

Nonisothermal Svstems

Definitions of heat transfer coefficients

Analytical calculations of heat transfer coefficients for forced convection through

tubes and slits

Heat transfer coefficients for forced convection in tubes

Heat transfer coefficients for forced convection around submerged objects

Heat transfer coefficients for forced convection through packed beds

Heat transfer coefficients for free and mixed convection

Heat transfer coefficients for condensation of pure vapors on solid surfaces

In Chapter

we saw how shell energy balances may be set up for various simple

problems and how these balances lead to differential equations from which the tem-

perature profiles may be calculated. We also saw in Chapter

that the energy bal-

ance over an arbitrary differential fluid element leads to a partial differential

equation-the energy equation-which may be used to set up more complex prob-

lems. Then in Chapter

we saw that the time-smoothed energy equation, together

with empirical expressions for the turbulent heat flux, provides a useful basis for

summarizing and extrapolating temperature profile measurements in turbulent sys-

tems. Hence, at this point the reader should have

fairly good appreciation for the

meaning of the equations of change for nonisothermal flow and their range of applic-

ability.

It should be apparent that all of the problems discussed have pertained to systems

of rather simple geometry and furthermore that most of these problems have contained

assumptions, such as temperature-independent viscosity and constant fluid density. For

some purposes, these solutions may be adequate, especially for order-of-magnitude esti-

mates. Furthermore, the study of simple systems provides the stepping stones to the dis-

cussion of more complex problems.

In this chapter we turn to some of the problems

which it is convenient or necessary

to use a less detailed analysis. In such problems the usual engineering approach is to for-

mulate energy balances over pieces of equipment, or parts thereof, as described in Chapter

15.

In the macroscopic energy balance thus obtained, there are usually terms that require

estimating the heat that is transferred through the system boundaries. This requires know-

ing the

heat transfer coefficient

for describing the interphase transport. Usually the heat

transfer coefficient is given, for the flow system of interest, as an empirical correlation of

514.1

Definitions of Heat Transfer Coefficients

423

the Nusselt number' (a dimensionless wall heat flux or heat transfer coefficient) as a func-

tion of the relevant dimensionless quantities, such as the Reynolds and Prandtl numbers.

This situation is not unlike that in Chapter

where we learned how to use dimen-

sionless correlations of the friction factor to solve momentum transfer problems. How-

ever, for nonisothermal problems the number of dimensionless groups is larger, the

types of boundary conditions are more numerous, and the temperature dependence of

the physical properties is often important.

addition, the phenomena of free convec-

tion, condensation, and boiling are encountered in nonisothermal systems.

We have purposely limited ourselves here to a small number of heat transfer formulas

and correlations-just enough to introduce the reader to the subject without attempting to

be encyclopedic. Many treatises and handbooks treat the subject in much greater depth."3,4,5~6

514.1

DEFINITIONS

HEAT TRANSFER COEFFICIENTS

Let us consider a flow system with the fluid flowing either in a conduit or around a solid

object. Suppose that the solid surface is warmer than the fluid, so that heat is being trans-

ferred from the solid to the fluid. Then the rate of heat flow across the solid-fluid inter-

face would be expected to depend on the area of the interface and on the temperature

drop between the fluid and the solid. It is customary to define a proportionality factor

(the

heat

transfer coefficient) by

Q=hAAT (14.1-1)

in which

is the heat flow into the fluid (J/hr or Btu/hr),

is a characteristic area, and AT

is a characteristic temperature difference. Equation 14.1-1 can also be used when the fluid

is cooled. Equation 14.1-1, in slightly different form, has been encountered in Eq. 10.1-2.

Note that

is not defined until the area

and the temperature difference AT have been

specified. We now consider the usual definitions for

for two types of flow geometry.

As an example of flow in conduits, we consider a fluid flowing through a circular tube

of diameter

(see Fig. 14.1-I), in which there is a heated wall section of length

and

varying inside surface temperature To(z), going from

To,

to To,. Suppose that the bulk

temperature Tb of the fluid (defined in

Eq.

10.8-33 for fluids with constant

and

ep)

in-

creases from

Tbl

T,,

in the heated section. Then there are three conventional definitions

of heat transfer coefficients for the fluid in the heated section:

This dimensionless group is named for

Ernst

Kraft

Wilhelm Nusselt

(1882-19571, the German

engineer who was the first major figure in the field

convective heat and mass transfer. See, for

example, W. Nusselt,

Zeits.

Ver. deutsck. Ing.,

53,1750-1755 (19091,

Forschungsarb. a.

Geb.

Ingenieurwes.,

No. 80,l-38, Berlin (1910), and

Gesundkeits-kg.,

38,477482,490496 (1915).

M. Jakob,

Heat Transfer,

Vol. 1 (1949) and Vol.

(19571, Wiley, New York.

Kays and

Crawford,

Convective Heat and Mass Transfer,

3rd edition, McGraw-Hill,

New York (1993).

Baehr and K. Stephan,

Heat and Mass Transfer,

Springer, Berlin (1998).

M. Rohsenow,

Hartnett, and

Cho (eds.),

Handbook of Heat Transfer,

McGraw-Hill,

New York (1998).

Grober,

Erk, and

Grigull,

Die Grundgesetze der Warmeiibertragung,

Springer, Berlin, 3rd

edition (1961).

424

Chapter 14 Interphase Transport in Nonisothermal Systems

"1"

Element of

"2"

Fig.

14.1-1.

Heat trans-

fer in a circular tube.

Inner surface

~nner surface

-L-

To1

Heated section

To2

with inner surface

temperature

TOM

That is,

is based on the temperature difference AT, at the inlet,

is based on the arith-

metic mean AT, of the terminal temperature differences, and h,, is based on the corre-

sponding logarithmic mean temperature difference AT,,. For most calculations

h,,

preferable, because it is less dependent on L/D than the other two, although it is not al-

ways used.' In using heat transfer correlations from treatises and handbooks, one must

be careful to note the definitions of the heat transfer coefficients.

If the wall temperature distribution is initially unknown, or if the fluid properties

change appreciably along the pipe, it is difficult to predict the heat transfer coefficients

defined above. Under these conditions, it is customary to rewrite

Eq.

14.1-2 in the differ-

ential form:

h,oc(~Ddz)(To

Tb)

hl,,(~Ddz)AT1, (14.1-5)

Here dQ is the heat added to the fluid over a distance dz along the pipe, ATloc is the local

temperature difference (at position

z),

and

h,,,

is the local heat transfer coefficient. This

equation is widely used in engineering design. Actually, the definition of h,,, and AT,,, is

not complete without specifying the shape of the element of area. In Eq. 14.1-5 we have

set dA

~Ddz, which means that

h,,,

and ATl,, are the mean values for the shaded area

dA in

Fig.

14.1-1.

As an example of flow around submerged objects, consider a fluid flowing around a

sphere of radius

whose surface temperature is maintained at a uniform value To. Sup-

pose that the fluid approaches the sphere with a uniform temperature T,. Then we

may define a mean heat transfer coeficient, h,, for the entire surface of the sphere by the re-

lation

~,(~TR~)(T,

T,)

(14.1-6)

The characteristic area is here taken to be the heat transfer surface (as in Eqs. 14.1-2 to

5),

whereas in

Eq.

6.1-5 we used the sphere cross section.

local coefficient can also be defined for submerged objects by analogy with

Eq.

14.1-5:

hloc(dA)(To

T,)

(14.1-7)

This coefficient is more informative than

because it predicts how the heat flux is dis-

tributed over the surface. However, most experimentalists report only h,,, which is easier

to measure.

ATJAT,

is between

0.5

and

2.0,

then

AT,

may be substituted for

ATl,,

and

for

h,,,

with a

maximum error of

4%.

This degree of accuracy is acceptable in most heat transfer calculations.

514.1 Definitions of Heat Transfer Coefficients

425

Table

14.1-1

Typical Orders of Magnitude for Heat

Transfer Coefficientsa

(W/m2

System (kcal/m2. hr

(Btu/ft2

Free convection

Gases

3-20 14

Liquids

100-600 20-120

Boiling water

1000-20,000 200-4000

Forced convection

Gases

1 0-1 00 2-20

Liquids

50-500 10-300

Water

500-10,000 100-2000

Condensing vapors

1000-1 00,000 200-20,000

Taken from

Grober,

Erk,

and

Grigull,

Wiirmeubertragung,

Springer, Berlin,

3rd

edition

(19551,

158.

When given

kcal/m2.

multiply by

0.204

get

in Btu/ft2

and

1.162

to get

W/m2.

For additional conversion factors,

see Appendix

Let us emphasize that the definitions of

and

must be made clear before

is de-

fined. Keep in mind, also, that

is not a constant characteristic of the fluid medium. On

the contrary, the heat transfer coefficient depffnds in a complicated way on many vari-

ables, including the fluid properties

(k,

CJ,

the system geometry, and the flow ve-

locity. The remainder of this chapter is devoted to predicting the dependence of

these quantities. Usually this is done by using experimental data and dimensional analy-

sis to develop correlations. It is also possible, for some very simple systems, to calculate

the heat transfer coefficient directly from the equations of change. Some typical ranges of

are given in Table 14.1-1.

We saw in 510.6 that, in the calculation of heat transfer rates between two fluid

streams separated by one or more solid layers, it is convenient to use an

overall

heat

trans-

fer coefficient,

U,,

which expresses the combined effect of the series of resistances through

which the heat flows. We give here a definition of

and show how to calculate it in the

special case of heat exchange between two coaxial streams with bulk temperatures

("hot") and

("cold), separated by a cylindrical tube of inside diameter Do and outside

diameter

D,:

+ln(D,/Do)

)

DoUo

D&"

2k"l

Dlhl

loc

Note that Uo is defined as a local coefficient. This is the definition implied in most design

procedures (see Example 15.4-1).

Equations 14.1-8 and

are, of course, restricted to thermal resistances connected

series.

In some situations there may be appreciable

parallel

heat flux at one or both

surfaces by radiation, and Eqs. 14.1-8 and

will require special modification (see

Example 16.5-2).

To illustrate the physical significance of heat transfer coefficients and illustrate one

method of measuring them, we conclude this section with an analysis of a hypothetical

set of heat transfer data.

426

Chapter 14 Interphase Transport in Nonisothermal Systems

EXAMPLE

14.1-1

Calculation of Heat

Transfer Coeficients

from Experimental

Data

SOLUTION

Isothermal Heated

section

Fig.

14.1-2.

Series of experiments

for measuring heat transfer coef-

ficients.

Pipe with

heated section

of length

Pipe with

heated section

of length

Pipe

with

heated section

of length

series of simulated steady-state experiments on the heating of air in tubes is shown in Fig.

14.1-2. In the first experiment, air at

Tbl

200.0°F is flowing in a 0.5-in. i.d. tube with fully de-

veloped laminar velocity profile in the isothermal pipe section for

0 the wall

temperature is suddenly increased to

212.O"F and maintained at that value for the re-

maining tube length LA. At

the fluid flows into a mixing chamber in which the cup-

mixing (or "bulk) temperature

T,,

is measured. Similar experiments are done with tubes of

different lengths,

L,,

LC, and so on, with the following results:

Experiment

(in.) 1.5 3.0

6.0 12.0 24.0

48.0

96.0

In all experiments, the air flow rate

is 3.0 lb,,/hr. Calculate

h,,

h,, h,,,

and the exit value of

h,,,

as functions of the L/D ratio.

First we make a steady-state energy balance over a length

of the tube, by stating that the

heat in through the walls plus the energy entering at

0 by convection equals the energy

leaving the tube at

The axial energy flux at the tube entry and exit may be calculated

from

Eq.

9.8-6.

For fully developed flow, changes in the kinetic energy flux

gpv2v

and the

work term

[T.

will be negligible relative to changes in the enthalpy flux. We also assume

that

pHv,,

so that the axial heat conduction term may be neglected. Hence the only con-

tribution to the energy flux entering and leaving with the flow will be the term containing the

enthalpy, which can be computed with the help of

Eq.

9.8-8

and the assumptions that the heat

capacity and density of the fluid are constant throughout. Therefore the steady-state energy

balance becomes simply "rate of energy flow in

rate of energy flow out," or

Using

Eq.

14.1-2 to evaluate

and rearranging gives