Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

1.4

Use of the Equations of Change to Solve Steady-State Problems

347

SOLUTION

Fig.

11.4-3.

The temperature and velocity profiles

the neighborhood of a vertical heated plate.

We postulate that

6,v,(y,

6,v,(y, z) and that

T(y, 2). We assume that the heated

fluid moves almost directly upward, so that v,

v,. Then the

and y-components of Eq.

11.3-2 give

p(z), so that the pressure is given to a very good approximation by

-dp/dz

0, which is the hydrostatic pressure distribution. The remaining equations of change are

Continuity

Motion

Energy

-----

in which

and

are evaluated at the ambient temperature TI. The dashed-underlined terms

will be omitted on the ground that momentum and energy transport by molecular processes

in the

direction is small compared with the corresponding convective terms on the left side

of the equations. These omissions should give a satisfactory description of the system except

for a small region around the bottom of the plate. With this simplification, the following

boundary conditions suffice to analyze the system up to

B.C.

aty=O, v,=v,=O and

T=T,

asy+

?m,

v,+O

and T+T1

Note that the temperature rise appears in the equation of motion and that the velocity distrib-

ution appears in the energy equation. Thus these equations are "coupled." Analytic solutions

of such coupled, nonlinear differential equations are very difficult, and we content ourselves

here with a dimensional analysis approach.

To do this we introduce the following dimensionless variables:

---

dimensionless temperature

dimensionless vertical coordinate

.4-40)

348

Chapter

The Equations of Change for Nonisothermal Systems

,r,

(&)

dimensionless horizontal coordinate

(--&)1'2uz

dimensionless vertical velocity

1.4-42)

(z)

dimensionless horizontal velocity

1.4-43)

in which

k/&

and

F~~(T~

TI).

When the equations of change, without the dashed-underlined terms, are written

terms of these dimensionless variables, we get

Continuity

Motion

Energy

The preceding boundary conditions then become

B.C.

One can see immediately from these equations and boundary conditions that the dimension-

less velocity components

and

and the dimensionless temperature

will depend on

and

and also on the Prandtl number, Pr. Since the flow is usually very slow in free convec-

tion, the terms in which Pr appears will generally be rather small; setting them equal to

zero

would correspond to the "creeping flow assumption." Hence we expect that the dependence

of the solution on the Prandtl number will be weak.

The average heat

flux

from one side of the plate may be written as

The integral may now be written in terms of the dimensionless quantities

in which the grouping Ra

GrPr is referred to as the

Rayleigk number.

Because

is a function

77,

and Pr, the derivative

dO/dv

is also a function of

,r,,

and Pr. Then

dO/dq,

evaluated

,r,

0, depends only on

and Pr. The definite integral over

thus a function of Pr. From

the remarks made earlier, we can infer that this function, called

will be only a weak func-

tion of the Prandtl number-that is, nearly a constant.

The preceding analysis shows that, even without solving the partial differential equa-

tions, we can predict that the average heat flux is proportional to the $-power of the tempera-

ture difference

(To

TI)

and inversely proportional to the +-power of

Both predictions

have been confirmed by experiment. The only thing we could not do was to find

as a func-

tion of Pr.

g11.4

Use of the Equations of Change to Solve Steady-State Problems

349

Adiabatic Frictionless

Processes in

Ideal

Gas

To determine that function, we have to make experimental measurements or solve Eqs.

11.4-44 to 49. In 1881, Lorenz3 obtained an approximate solution to these equations and found

0.548. Later, more refined calculations4 gave the following dependence of

on Pr:

Pr 0.73 (air)

100 1000

0.518 0.535

0.620 0.653 0.665 0.670

These values of

are nearly in exact agreement with the best experimental measurements in

the laminar flow range (i.e., for GrPr

lo9h5

Develop equations for the relationship of local pressure to density or temperature in a stream

of ideal gas in which the momentum flux

and the heat flux

are negligible.

SOLUTION

With

and

neglected, the equation of energy [Eq.

(1)

in Table 11.4-11 may be rewritten as

For an ideal gas,

RT/M, where M is the molecular weight of the gas, and Eq. 11.4-52

becomes

Dividing this equation by

and assuming the molar heat capacity

to be constant,

we can again use the ideal gas law to get

Hence the quantity in parentheses is a constant along the path of a fluid element, as is its an-

tilogarithm, so that we have

TC,/R

constant

1.4-55)

This relation applies to all thermodynamic states

that a fluid element encounters as it

moves along with the fluid.

Introducing the definition

tp/Pv

and the ideal gas relations

R and

pRT/M, one obtains the related expressions

p'y-l"y~-'

constant

1.4-56)

and

pp-Y

constant

1.4-57)

These last three equations find frequent use in the study of frictionless adiabatic processes in

ideal gas dynamics. Equation 11.4-57 is

famous relation well worth remembering.

L. Lorenz,

Wiedemann's Ann. der Physik u. Chemie,

13,42247,582406 (1881). See also

Grigull,

Die Grundgesetze der Warrneiibertragung,

Springer-Verlag, Berlin, 3rd edition (1955), pp. 263-269.

%ee

Whitaker,

Fundamental Principles

Heat Transfer,

Krieger, Malabar Fla. (1977), g5.11. The

limiting case of Pr

has been worked out numerically by E.

LeFevre [Heat Div. Paper 113, Dept.

Sci. and Ind. Res., Mech. Engr. Lab. (Great Britain), Aug. 19561 and it was found that

Equation 11.4-51a corresponds to the value

0.670 above.

This

result has been verified experimentally

Wilke,

W. Tobias, and

Eisenberg,

Electrochem. Soc.,

100,513-523 (1953), for the analogous

mass transfer problem.

For

analysis of free convection in three-dimensional creeping flow, see W.

Stewart,

Int.

Heat

and Mass Transfer,

14,1013-1031 (1971).

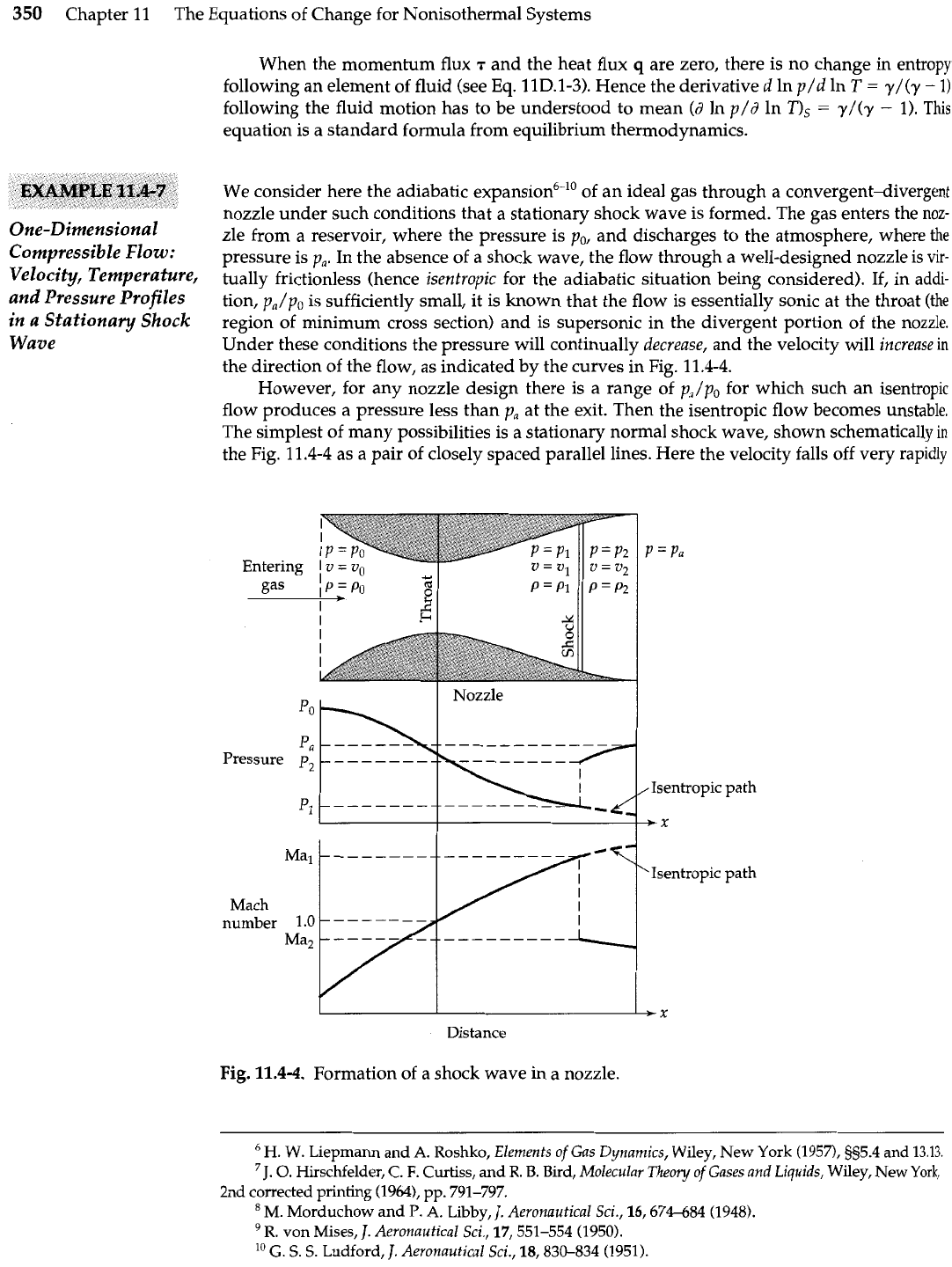
350

Chapter 11 The Equations of Change for Nonisothermal Systems

EXAMPLE

11.47

One-Dimensional

Compressible Flow:

Velocity, Temperature,

and Pressure Profiles

Stationa

Shock

Wave

When the momentum flux

and the heat flux

are zero, there is no change in entropy

following an element of fluid (see Eq. 11D.1-3). Hence the derivative d In p/d In

y/(y

following the fluid motion has to be understood to mean

In p/d In

T)s

y/(y

1).

This

equation is a standard formula from equilibrium thermodynamics.

We consider here the adiabatic expansion6-lo of an ideal gas through a convergent-divergent

nozzle under such conditions that a stationary shock wave is formed. The gas enters the noz-

zle from a reservoir, where the pressure is po, and discharges to the atmosphere, where

the

pressure is p,. In the absence of a shock wave, the flow through a well-designed nozzle is vir-

tually frictionless (hence isentropic for the adiabatic situation being considered).

If,

in addi-

tion, p,/po is sufficiently small, it is known that the flow is essentially sonic at the throat

(the

region of minimum cross section) and is supersonic in the divergent portion of the nozzle.

Under these conditions the pressure will continually decrease, and the velocity will increase

the direction of the flow, as indicated by the curves in Fig. 11.4-4.

However, for any nozzle design there is a range of p,/po for which such an isentropic

flow produces a pressure less than p, at the exit. Then the isentropic flow becomes unstable.

The simplest of many possibilities is

stationary normal shock wave, shown schematically

the Fig. 11.4-4 as a pair of closely spaced parallel lines. Here the velocity falls off very rapidly

gas

Nozzle

Mach

Distance

Fig.

11.4-4.

Formation of a shock wave in a nozzle.

Isentropic path

Liepmann and

Roshko,

Elements of Gas Dynamics,

Wiley, New York (1957), 995.4 and 13.13.

Hirschfelder,

Curtiss, and

Bird,

Molecular Theory of Gases and Liquids,

Wiley, New

York,

2nd corrected printing (1964), pp. 791-797.

M. Morduchow and

Libby,

Aeronautical Sci.,

16,674-684 (1948).

von Mises,

Aeronautical Sci.,

17,551-554 (1950).

Ludford,

Aeronautical Sci.,

18,830-834 (1951).

511.4 Use of the Equations of Change to Solve Steady-State Problems

351

SOLUTION

to a subsonic value, while 60th the pressure and the density rise. These changes take place in

an extremely thin region, which may therefore be considered locally one-dimensional and

laminar, and they are accompanied by a very substantial dissipation of mechanical energy.

Viscous dissipation and heat conduction effects are thus concentrated in an extremely small

region of the nozzle, and it is the purpose of the example to explore the fluid behavior there.

For simplicity the shock wave will be considered normal to the fluid streamlines; in practice,

much more complicated shapes are often observed. The velocity, pressure, and temperature

just upstream of the shock can be calculated and will be considered as known for the pur-

poses of this example.

Use the three equations of change to determine the conditions under which a shock wave

is possible and to find the velocity, temperature, and pressure distributions in such a shock

wave. Assume steady, one-dimensjonal flow of an ideal gas, neglect the dilatational viscosity

and ignore changes of p,

and

with temperature and pressure.

The equations of change in the neighborhood of the stationary shock wave may be simpli-

fied to

Continuity:

;s;

PV,

1.4-58)

Motion:

Energy:

The energy equation is in the form of Eq.

of Table 11.4-1, written for an ideal gas in a steady-

state situation.

The equation of

continuity

may be integrated to give

in which

and

are quantities evaluated a short distance upstream from the shock.

In the

energy

equation we eliminate

pv,

by use of Eq. 11.4-61 and

dp/dx

by using the

equation of motion to get (after some rearrangement)

We next move the second term on the right side over to the left side and divide the entire

equation by

p,v,.

Then each term is integrated with respect to

to give

in which

is a constant of integration and Pr

C,p/k.

For most gases Pr is between 0.65 and

0.85, with an average value close to 0.75. Therefore, to simplify the problem we set Pr equal to

Then Eq. 11.4-63 becomes a first-order, linear ordinary differential equation, for which the

solution is

Since

t,T

iv;

cannot increase without limit in the positive

direction, the second integra-

tion constant

CI1

must be zero. The first integration constant is evaluated from the upstream

conditions, so that

Of course, if we had not chosen Pr to be

a numerical integration of Eq. 11.4-63 would have

been required.

352

Chapter 11 The Equations of Change for Nonisothermal Systems

Next we substitute the integrated continuity equation into the equation of

motion

and in-

tegrate once to obtain

Evaluation of the constant

CIIl

from upstream conditions, where dv,/dx

gives

CIII

plv:

plIv:

(RTl/M)I. We now multiply both sides by vx and divide by plvl. Then,

with the help of the ideal gas law,

pRT/M, and Eqs. 11.4-61 and 65, we may eliminate

from Eq. 11.4-60 to obtain a relation containing only v, and

as variables:

This equation can, after considerable rearrangement, be rewritten in terms of dimensionless

variables:

The relevant dimensionless quantities are

dimensionless velocity

1.4-69)

dimensionless coordinate

1.4-70)

Mach number at the upstream condition

I--

(1 1.4-71)

The reference length

is the mean free path defined in Eq. 1.4-3 (with

eliminated by use

Eq. 1.4-9):

We may integrate Eq. 11.4-68 to obtain

explPMa1(l

a)((

&)I

a)"

This equation describes the dimensionless velocity distribution

4(5)

containing an integration

constant

x,/h, which specifies the position of the shock wave in the nozzle; here

is con-

sidered to be known. It can be seen from the plot of Eq. 11.4-85 in Fig. 11.4-5 that shock

waves

Fig.

11.4-5.

Velocity distri-

bution in

stationary shock

xo),

lo5

wave.

911.5

Dimensional Analysis of the Equations of Change for Nonisothermal Systems

353

0.00025 in. wire

0.002

in.

wire

Theory, equations of

Dimensionless position in flow direction

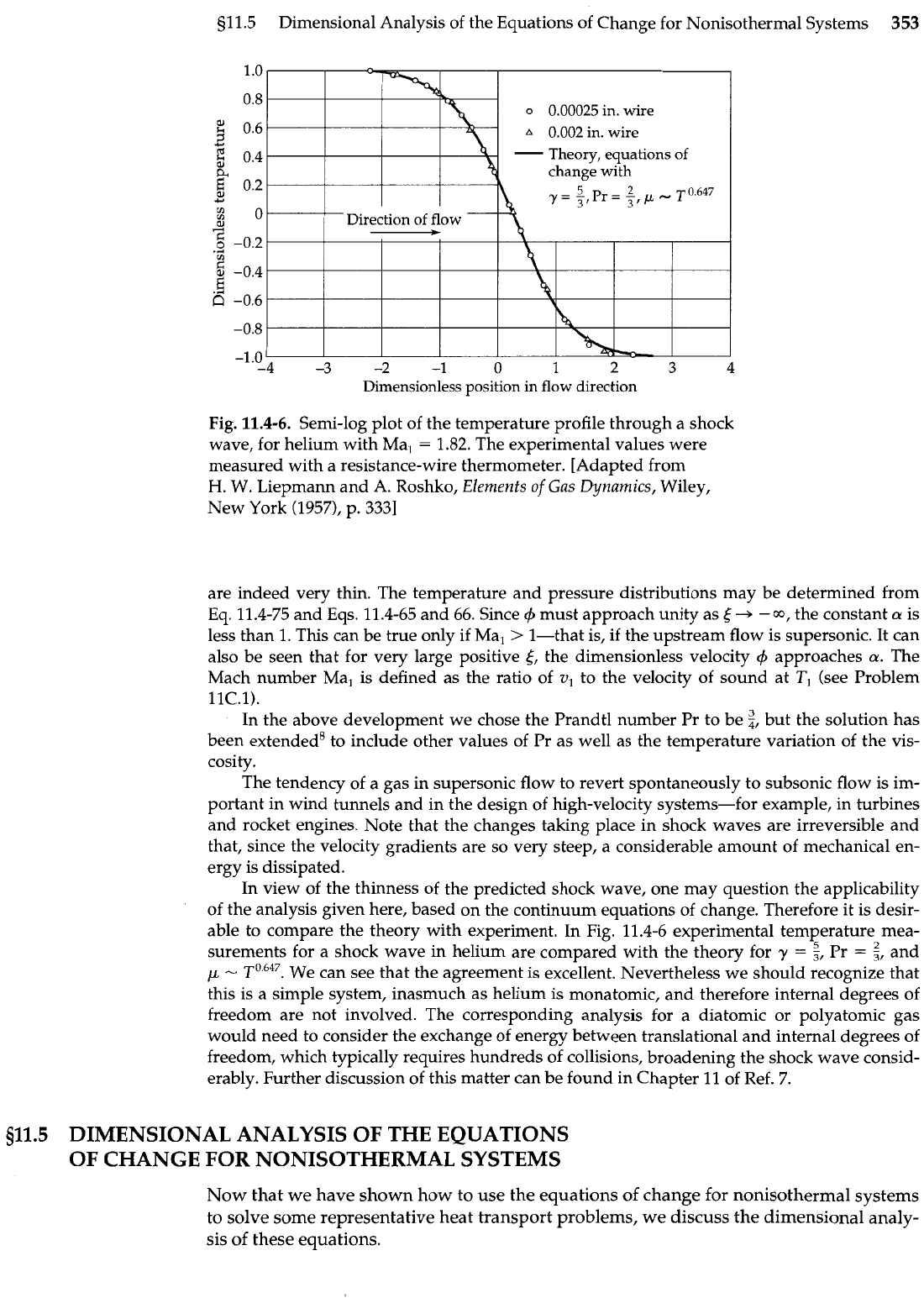
Fig.

11.4-6.

Semi-log plot of the temperature profile through a shock

wave, for helium with Ma,

1.82.

The experimental values were

measured with a resistance-wire thermometer. [Adapted from

W. Liepmann and A. Roshko, Elements

Gas Dynamics, Wiley,

New York (1957), p.

3331

are indeed very thin. The temperature and pressure distributions may be determined from

Eq. 11.4-75 and Eqs. 11.4-65 and 66. Since

must approach unity as

-a,

the constant

less than 1. This can be true only if Ma,

1-that is, if the upstream flow is supersonic. It can

also be seen that for very large positive 6, the dimensionless velocity

approaches

The

Mach number Ma, is defined as the ratio of

to the velocity of sound at

(see Problem

11C.1).

In the above development we chose the Prandtl number Pr to be

but the solution has

been extended8 to include other values of Pr as well as the temperature variation of the vis-

cosity.

The tendency of a gas in supersonic flow to revert spontaneously to subsonic flow is im-

portant in wind tunnels and in the design of high-velocity systems-for example, in turbines

and rocket engines. Note that the changes taking place in shock waves are irreversible and

that, since the velocity gradients are so very steep, a considerable amount of mechanical en-

ergy is dissipated.

In view of the thinness of the predicted shock wave, one may question the applicability

of the analysis given here, based on the continuum equations of change. Therefore it is desir-

able to compare the theory with experiment. In Fig. 11.4-6 experimental temperature mea-

surements for a shock wave in helium are compared with the theory for

and

We can see that the agreement is excellent. Nevertheless we should recognize that

this is a simple system, inasmuch as helium is monatomic, and therefore internal degrees of

freedom are not involved. The corresponding analysis for a diatomic or polyatomic gas

would need to consider the exchange of energy between translational and internal degrees of

freedom, which typically requires hundreds of collisions, broadening the shock wave consid-

erably. Further discussion of this matter can be found in Chapter

of Ref. 7.

511.5

DIMENSIONAL ANALYSIS OF THE EQUATIONS

OF CHANGE FOR NONISOTHERMAL SYSTEMS

Now that we have shown how to use the equations

change for nonisothermal systems

to solve some representative heat transport problems, we discuss the dimensional analy-

sis of these equations.

354

Chapter 11 The Equations of Change for Nonisothermal Systems

Just as the dimensional analysis discussion in 53.7 provided an introduction for the

discussion of friction factors in Chapter

the material in this section provides the back-

ground needed for the discussion of heat transfer coefficient correlations in Chapter 14.

As in Chapter 3, we write the equations of change and boundary conditions in dimen-

sionless form. In this way we find some dimensionless parameters that can be used

characterize nonisothermal flow systems.

We shall see, however, that the analysis of nonisothermal systems leads us to

larger number of dimensionless groups than we had in Chapter 3. As a result, greater re-

liance has to be placed on judicious simplifications of the equations of change and on

carefully chosen physical models. Examples of the latter are the Boussinesq equation

motion for free convection (511.3) and the laminar boundary layer equations (512.4).

As in 53.7, for the sake of simplicity we restrict ourselves to a fluid with constant

and

tp.

The density is taken to be

?F(T

in the

term in the equation

motion, and

everywhere else (the "Boussinesq approximation"). The equations

change then become with

sgh

expressed as

Continuity:

0 (1 1.5-1)

Motion:

Energy:

We now introduce quantities made dimensionless with the characteristic quantities (sub-

script 0 or 1) as follows:

Here lo,

v,,

and

are the reference quantities introduced in s3.7, and

and

are

temperatures appearing in the boundary conditions. In Eq. 11.5-2 the value

is the

temperature around which the density

was expanded.

In terms of these dimensionless variables, the equations of change in Eqs. 11.5-1 to

take the forms

Energy:

The characteristic velocity can be chosen in several ways, and the consequences of

the

choices are summarized in Table 11.5-1. The dimensionless groups appearing in

Eqs.

11.5-8 and

along with some combinations of these groups, are summarized in Table

11.5-2. Further dimensionless groups may arise in the boundary conditions or in the

equation of state. The Froude and Weber numbers have already been introduced in

93.7,

and the Mach number in Ex. 11.4-7.

We already saw in Chapter 10 how several dimensionless groups appeared in the

solution of nonisothermal problems. Here we have seen that the same groupings appear

naturally when the equations of change are made dimensionless. These dimensionless

groups are used widely in correlations of heat transfer coefficients.

s11.5

Dimensional Analysis of the Equations of Change for Nonisothermal Systems

355

Table

11.5-1

Dimensionless Groups in Equations 11.5-7,8, and

Special Forced Free Free

cases

convection Intermediate convection convection

(A)

(B)

Choice

for

v/10

/lo

RePr RePr

Neglect Neglect

Notes:

For forced convection and forced-plus-free ("intermediate") convection,

is generally

taken to be the approach velocity (for flow around submerged objects) or an average

velocity in the system (for flow in conduits).

For free convection there are two standard choices for

v,,

labeled as

and

g10.9,

Case

arises naturally. Case

proves convenient if the assumption of creeping flow is

appropriate, so that

D+/D~

can be neglected (see Example

11.5-2).

Then a new

dimensionless pressure difference

Pry, different from

in Eq.

3.7-4,

can be

introduced, so that when the equation of motion is divided by Pr, the only dimensionless

group appearing in the equation is GrPr. Note that in Case

no dimensionless groups

appear in the equation of energy.

It is sometimes useful to think of the dimensionless groups as ratios of various

forces or effects in the system, as shown in Table

11.5-3.

For example, the inertia1 term in

the equation

motion is

p[v

Vvl

and the viscous term is To get "typical" values

of these terms, replace the variables by the characteristic "yardsticks" used in construct-

ing

dimensionless variables. Hence replace p[v

Vv]

by p@lo, and replace

/AV%

,!~v~/li to get rough orders of magnitude. The ratio of these two terms then gives the

Reynolds number, as shown in the table. The other dimensionless groups are obtained in

similar fashion.

Table

11.5-2

Dimensionless Groups Used in

Nonisothermal Systems

[lov,p/p]l

[lov,/v]l

Reynolds number

[epp/k]

[v/a]

Prandtl number

bp(T,

T,)I;/S?]

Grashof number

[[pv~/k(~l

To)]

Brinkman number

RePr

Pkclet number

GrPr

Rayleigh number

&-/R

=Z&erf number

356

Chapter

The Equations of Change for Nonisothermal Systems

Table

11.5-3

Physical Interpretation of Dimensionless Groups

~v?j/lo

inertial force

Re=--

v0/ viscous force

pv?j/Io

inertial force

Fr=--

P8 gravity force

pg/3(Tl

To)

buoyant force

Re2

PV?~

inertial force

~C,V&T~

heat transport by convection

RePr

(

)

heat transport by conduction

p(vo/lo)2

heat production by viscous dissipation

- -

kU-1

To)/G

heat transport by conduction

low value for the Reynolds number means that viscous forces are large in compar-

ison with inertial forces.

low value of the Brinkrnan number indicates that the heat

produced by viscous dissipation can

transported away quickly by heat conduction.

When ~r/~e* is large, the buoyant force is important in determining the flow pattern.

Since dimensional analysis is an art requiring judgment and experience, we give

three illustrative examples. In the first two we analyze forced and free convection in sim-

ple geometries. In the third we discuss scale-up problems in a relatively complex piece

of equipment.

EXAMPLE

125-1

Temperature

Distribution about

Long

Cylinder

It is desired to predict the temperature distribution in a gas flowing about a long, internally

cooled cylinder (system

from experimental measurements on a one-quarter scale model

(system 11). If possible the same fluid should be used in the model as in the full-scale system.

The system, shown in Fig. 11.5-1, is the same as that in Example 3.7-1 except that it is now

nonisothermal. The fluid approaching the cylinder has a speed

and a temperature T,, and

the cylinder surface is maintained at To, for example, by the boiling of a refrigerant contained

within it.

Show by means of dimensional analysis how suitable experimental conditions can be

chosen for the model studies. Perform the dimensional analysis for the "intermediate case" in

Table 11.5-1.

SOLUTION

The two systems, I and 11, are geometrically similar. To ensure dynamical similarity, as

pointed out in 53.7, the dimensionless differential equations and boundary conditions must

be the same, and the dimensionless groups appearing in them must have the same numerical

values.

Here we choose the characteristic length to be the diameter

of the cylinder, the charac-

teristic velocity to be the approach velocity

of the fluid, the characteristic pressure to be the

pressure at

and

0, and the characteristic temperatures to be the temperature T,

the approaching fluid and the temperature To of the cylinder wall. These characteristic quan-

tities will carry a label

or I1 corresponding to the system being described.

Both systems are described by the dimensionless differential equations given in

Eqs.

11.5-7 to

and by boundary conditions

B.C. 1

B.C.