Bird J. Electrical Circuit Theory and Technology
Подождите немного. Документ загружается.

908 Electrical Circuit Theory and Technology
When t D 6ms, v
R
D 110
1 e
[56ð10
3
/50ð10
3
D 1101 e
0.60
D 1100.45119 D 49.63 V
(d) From equation (45.15), the voltage across the inductance,
v
L
D Ve
Rt/L
When t D 6 ms,
v
L
D 110e
56ð10
3
/50ð10
3
D 110 e
0.60
D 60.37 V
(Note that at t D 6 ms,
v
L
C v
R
D 60.37 C 49.63 D 110 V D supply p.d., V
(e) When current i reaches 15 A,
15 D
V
R
1 e
Rt/L
from equation (45.13)
i.e., 15 D
110
5
1 e
5t/50ð10
3
15
5
110
D 1 e
100t
and e
100t
D 1
75
110
Hence 100t D ln
1
75
110
and time, t D
1
100
ln
1
75
100
D 0.01145 s or 11.45 ms
Current decay
If after a period of time the step voltage V applied to the circuit of
Figure 45.6 is suddenly removed by opening the switch, then from equa-
tion (45.11),
0 D L
di
dt
C iR
Rearranging gives: L
di
dt
DiR or
di
dt
D
iR
L
Separating the variables gives:
di
i
D
R
L
dt
and integrating both sides gives:
di
i
D
R
L
dt
lni D
R
L
t C k45.16

Transients and Laplace transforms 909
At t D 0 (i.e., when the switch is opened),
i D I
D
V
R
, the steady state current
then ln I D 0 C k
Substituting k D lnI into equation (45.16) gives:
lni D
R
L
t C lnI
Rearranging gives: lni lnI D
R
L
t
ln
i
I
D
R
L
t
i
I
D e
Rt/L
and current,
i = Ie
−Rt=L
or
V
R
e
−Rt=L
45.17
i.e., the current i decays exponentially to zero.
From Figure 45.6,
v
R
D iR D R
V
R
e
Rt/L
from equation (45.17)
i.e.,
v
R
= Ve
−Rt=L
45.18
The voltage across the coil,
v
L
D L
di
dt
D L
d
dt
V
R
e
Rt/L
from equation (45.17)
D L
V
R
R
L
e
Rt/L
Hence the magnitude of v
L
is given by:
v
L
= Ve
−Rt=L
45.19
Hence both
v
R
and v
L
decay exponentially to zero.
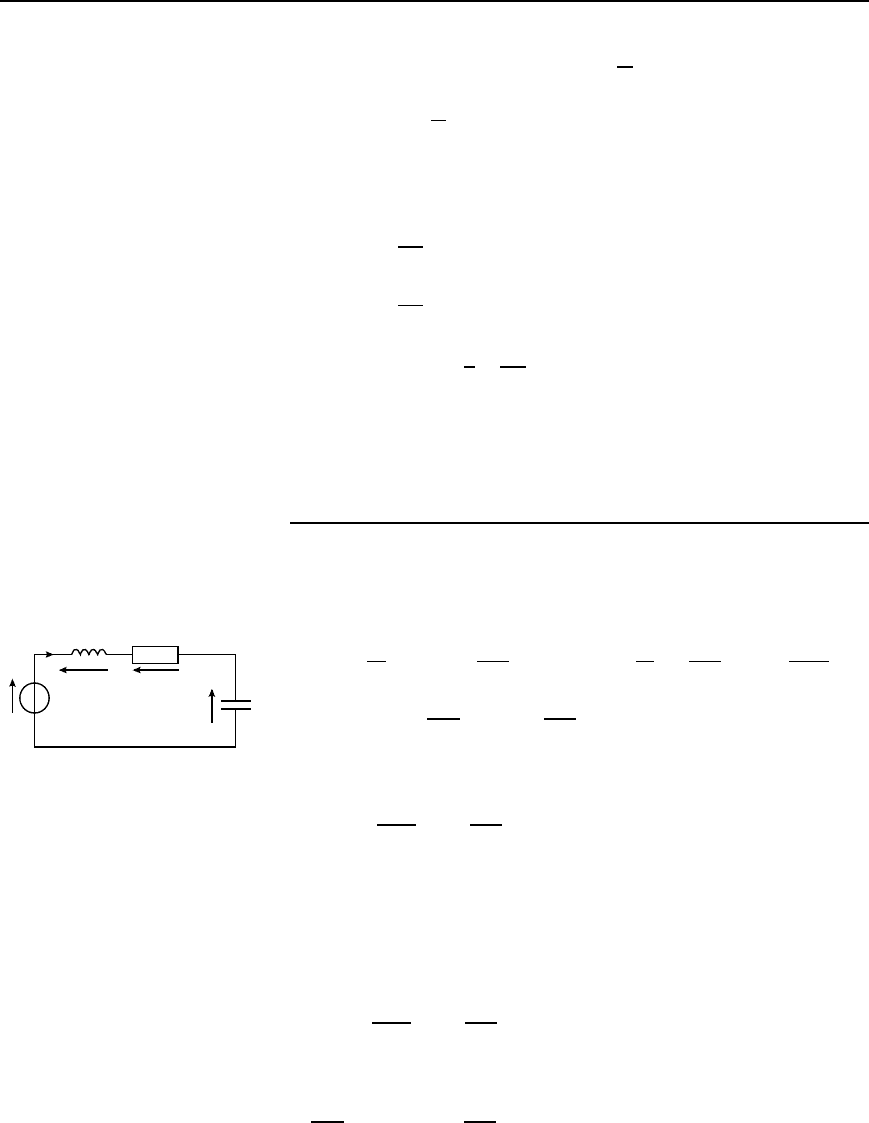
Problem 4. In the circuit shown in Figure 45.8, a current of 5 A
flows from the supply source. Switch S is then opened. Determine
(a) the time for the current in the 2 H inductor to fall to 200 mA,
and (b) the maximum voltage appearing across the resistor.
(a) When the supply is cut off, the circuit consists of just the 10
resistor and the 2 H coil in parallel. This is effectively the same
circuit as Figure 45.6 with the supply voltage zero.
2 H
S5 A
V
10 Ω
Figure 45.8
910 Electrical Circuit Theory and Technology
From equation (45.17), current i D
V
R
e
Rt/L
In this case
V
R
D 5 A, the initial value of current.
When i D 200 mA or 0.2 A,
0.2 D 5e
10t/2
i.e.,
0.2
5
D e
5t
thus ln
0.2
5
D5t
and time, t D
1
5
ln
0.2
5
D 0.644 s or 644 ms
(b) Since the current through the coil can only return through the 10
resistance, the voltage across the resistor is a maximum at the
moment of disconnection, i.e.,
v
R
m
D IR D 510 D 50 V
45.4 L–R–C series
circuit response
For the circuit shown in Figure 45.9, from Kirchhoff’s voltage law,
V D
v
L
C v
R
C v
C
45.20
v
L
D L
di
dt
and i D C
d
v
C
dt
, hence
v
L
D L
d
dt
C
d
v
C
dt
D LC
d
2
v
C
dt
2
v
R
D iR D
C
d
v
C
dt
R D RC
d
v
C
dt
R
V
L
v
L
v
R
v
C
C
i
Figure 45.9
Hence from equation (45.20):
V D LC
d
2
v
C
dt
2
C RC
d
v
C
dt
C
v
C
45.21
This is a linear, constant coefficient, second order differential
equation.(For the solution of second order differential equations, see
Higher Engineering Mathematics).
To determine the transient response, the supply p.d., V, is made equal
to zero,
i.e., LC
d
2
v
C
dt
2
C RC
d
v
C
dt
C
v
C
D 0 45.22
A solution can be found by letting
v
C
D Ae
mt
, from which,
d
v
C
dt
D Ame
mt
and
d
v
C
dt
2
D Am
2
e
mt

Transients and Laplace transforms 911
Substituting these expressions into equation (45.22) gives:
LCAm
2
e
mt
C RCAme
mt
C Ae
mt
D 0
i.e., Ae
mt
m
2
LC C mRC C 1 D 0
Thus
v
C
D Ae
mt
is a solution of the given equation provided that
m
2
LC C mRC C 1 D 0 45.23
This is called the auxiliary equation.
Using the quadratic formula on equation (45.23) gives:
m D
RC š
[RC
2
4LC1]
2LC
D
RC š
R
2
C
2
4LC
2LC
i.e., m D
RC
2LC
š
R
2
C
2
4LC
2LC
2
D
R
2L
š
R
2
C
2
4L
2
C
2
4LC
4L
2
C
2
D
R
2L
š
R
2L
2
1
LC
45.24
This equation may have either:
(i) two different real roots, when R/2L
2
>1/LC, when the circuit
is said to be overdamped since the transient voltage decays very
slowly with time, or
(ii) two real equal roots, when R/2L
2
D 1/LC, when the circuit is
said to be critically damped since the transient voltage decays in
the minimum amount of time without oscillations occurring, or
(iii) two complex roots, when R/2L
2
<1/LC, when the circuit is
said to be underdamped since the transient voltage oscillates about
the final steady state value, the oscillations eventually dying away
to give the steady state value, or
(iv) if R
= 0 in equation (45.24), the oscillations would continue
indefinitely without any reduction in amplitude—this is the
undamped condition.
Damping in discussed again in Section 45.8 with typical current responses
sketched in Figure 45.28 on page 947.
Problem 5. A series L –R–C circuit has inductance, L D 2mH,
resistance, R D 1k and capacitance, C D 5
µF. (a) Determine
whether the circuit is over, critical or underdamped. (b) If C D
5 nF, determine the state of damping.
912 Electrical Circuit Theory and Technology
(a)
R
2L
2
D
10
3
22 ð 10
3
2
D
10
12
16
D 6.25 ð 10
10
1
LC
D
1
2 ð 10
3
5 ð 10
6
D
10
9
10
D 10
8
Since
R
2L
2
>
1
LC
the circuit is overdamped.
(b) When C D 5 nF,
1
LC
D
1
2 ð 10
3
5 ð 10
9
D 10
11
Since
R
2L
2
<
1
LC
the circuit is underdamped.
Problem 6. In the circuit of problem 5, what value of capacitance
will give critical damping ?
For critical damping:
R
2L
2
D
1
LC
from which, capacitance ,
C D
1
L
R
2L
2
D
1
L
R
2
4L
2
D
4L
2
LR
2
D
4L
R
2
D
42 ð 10
3
10
3
2
D 8 ð 10
9
For8nF
Roots of the auxiliary equation
With reference to equation (45.24):
(i) when the roots are real and different,saym D ˛ and m D ˇ, the
general solution is
v
C
= Ae
at
Y Be
bt
45.25
where ˛ D
R
2L
C
R
2L
2
1
LC
and
ˇ D
R
2L
R
2L
2
1
LC
Transients and Laplace transforms 913
(ii) when the roots are real and equal,saymD ˛ twice, the general
solution is
v
C
= .At Y B/e
at
45.26
where ˛ D
R
2L
(iii) when the roots are complex, say m D ˛ š jˇ, the general solu-
tion is
v
C
= e
at
f
Acos bt Y B sin bt
g
45.27
where ˛ D
R
2L
and ˇ D
1
LC
R
2L
2
(45.28)
To determine the actual expression for the voltage under any given initial
condition, it is necessary to evaluate constants A and B in terms of
v
C
and current i. The procedure is the same for each of the above three
cases. Assuming in, say, case (iii) that at time t D 0,
v
C
D v
0
and iD
Cd
v
C
/dt D i
0
then substituting in equation (45.27):
v
0
D e
0
f
A cos 0 C B sin 0
g
i.e.,
v
0
D A 45.29
Also, from equation (45.27),
d
v
C
dt
D e
˛t
[Aˇ sin ˇt C Bˇ cos ˇt]
C [A cos ˇt C B sin ˇt]
˛e
˛t
45.30
by the product rule of differentiation
When t D 0,
d
v
C
dt
D e
0
[0 C Bˇ] C [A]
˛e
0
D Bˇ C ˛A
Hence at t D 0, i
0
D C
d
v
C
dt
D CBˇ C ˛A
From equation (45.29), A D
v
0
hence i
0
D CBˇ C ˛v
0
D CBˇ C C˛v
0
from which, B =
i
0
− Cav
0
Cb
45.31
Problem 7. A coil has an equivalent circuit of inductance 1.5 H
in series with resistance 90 . It is connected across a charged
5
µF capacitor at the moment when the capacitor voltage is 10 V.
Determine the nature of the response and obtain an expression for
the current in the coil.

914 Electrical Circuit Theory and Technology
R
2L
2
D
90
21.5
2
D 900 and
1
LC
D
1
1.55 ð 10
6
D 1.333 ð 10
5
Since
R
2L
2
<
1
LC
the circuit is underdamped.
From equation (45.28),
˛ D
R
2L
D
90
21.5
D30
and ˇ D
1
LC
R
2L
2
D
[1.333 ð 10
5
900] D 363.9
With
v
0
D 10Vandi
0
D 0, from equation (45.29), v
0
D A D 10
and from equation (45.31), B D
i
0
C˛v
0
Cˇ
D
0 5 ð 10
6
3010
5 ð 10
6
363.9
D
300
363.9
D 0.8244
Current, i D C
d
v
C
dt
, and from equation (45.30),
i D Cfe
30t
[10363.9 sin ˇt C 0.8244363.9 cosˇt]
C 10cosˇt C 0.8244 sinˇt30e
30t
g
D Cfe
30t
[3639sinˇt C 300cosˇt 300 cos ˇt
24.732sinˇt]g
D Ce
30t
[3663.732sinˇt]
D5 ð 10
6
3663.732e
30t
sinˇt
i.e., current, i
= −0.0183e
−30t
sin363.9t amperes
Further problems on R–C, R–L and L –R–C series circuits may be found
in Section 45.10. problems 1 to 8, page 952.
45.5 Introduction to
Laplace transforms
The solution of most electrical problems can be reduced ultimately to
the solution of differential equations and the use of Laplace transforms
provides an alternative method to those used previously. Laplace trans-
forms provide a convenient method for the calculation of the complete
response of a circuit. In this section and in Section 45.6 the technique
of Laplace transforms is developed and then used to solve differential
equations. In Section 45.7 Laplace transforms are used to analyse transient
responses directly from circuit diagrams.
Transients and Laplace transforms 915
Definition of a Laplace transform
The Laplace transform of the function of time ft is defined by the
integral
1
0
e
st
ftdt where s is a parameter
There are various commonly used notations for the Laplace transform of
ft and these include
Lfftg or Lfftg or Lf or Lf or fs
Also the letter p is sometimes used instead of s as the parameter. The
notation used in this chapter will be ft for the original function and
Lfftg for its Laplace transform,
i.e.,
LfftgD
1
0
e
st
ftdt 45.32
Laplace transforms of elementary functions
Using equation (45.32):
(i) when f .t/
= 1, Lf1gD
1
0
e
st
1dt D
e
st
s
1
0
D
1
s
e
s1
e
0
D
1
s
[0 1] D
1
s
(provide s>0)
(ii) when f .t/
= k, LfkgDkLf1gDk
1
s
D
k
s
from (i) above
(iii) when f .t/ D e
at
, Lfe
at
gD
1
0
e
st
e
at
dt D
e
sat
dt
from the laws of indices
D
e
sat
s a
1
0
D
1
s a
0 1
D
1
s − a
(provided s>a)
(iv) when f .t/
= t, LftgD
1
0
e
st
tdtD
te
st
s
e
st
s
dt
1
0
D
te
st
s
e
st
s
2
1
0
by integration by parts
D
1e
s1
s
e
s1
s
2
0
e
0
s
2
D 0 0
0
1
s
2
since 1ð0 D 0
D
1
s
2
provided s>0
916 Electrical Circuit Theory and Technology
(v) when f .t/ = cos!t, LfcosωtgD
1
0
e
st
cosωt dt
D
e
st
s
2
C ω
2
ω sinωt s cosωt
1
0
by integration by parts twice
D
s
s
2
Y !
2
provided s>0
A list of standard Laplace transforms is summarized in Table 45.1 on
page 917. It will not usually be necessary to derive the transforms as
above—but merely to use them.
The following worked problems only require using the standard list of
Table 45.1.
Problem 8. Find the Laplace transforms of (a) 1 C 2t
1
3
t
4
(b) 5e
2t
3e
t
(a) Lf1 C 2t
1
3
t
4
gDLf1gC2Lftg
1
3
Lft
4
g
D
1
s
C 2
1
s
2
1
3
4!
s
4C1
from2,7and9ofTable45.1
D
1
s
C
2
s
2
1
3
4 ð 3 ð 2 ð1
s
5
D
1
s
C
2
s
2
8
s
5
(b) Lf5e
2t
3e
t
gD5Lfe
2t
g3Lfe
t
g
D 5
1
s 2
3
1
s 1
from 3 of Table 45.1
D
5
s 2
3
s C 1
D
5s C 1 3s 2
s 2s C 1
D
2s C 11
s
2
s 2
Problem 9. Find the Laplace transform of 6sin3t 4 cos 5t
Lf6sin3t 4 cos 5tgD6Lfsin3tg4Lfcos5tg
D 6
3
s
2
C 3
2
4
s
s
2
C 5
2
from5and6ofTable45.1
D
18
s
2
Y 9
4s
s
2
Y 25
Transients and Laplace transforms 917
TABLE 45.1 Standard Laplace Transforms
Time function f(t) Laplace transform
LfftgD
1
0
e
st
ftdt
1. υ (unit impulse) 1
2. 1 (unit step function)
1
s
3. e
at
(exponential function)
1
s a
4. unit step delayed by T
e
sT
s
5. sin ωt (sine wave)
ω
s
2
C ω
2
6. cos ωt (cosine wave)
s
s
2
C ω
2
7. t (unit ramp function)
1
s
2
8. t
2
2!
s
3
9. t
n
n D 1, 2, 3..
n!
s
nC1
10. cosh ωt
s
s
2
ω
2
11. sinh ωt
ω
s
2
ω
2
12. e
at
t
n
n!
s a
nC1
13. e
at
sinωt (damped sine wave)
ω
s C a
2
C ω
2
14. e
at
cosωt (damped cosine wave)
s C a
s C a
2
C ω
2
15. e
at
sinhωt
ω
s C a
2
ω
2
16. e
at
coshωt
s C a
s C a
2
ω
2
