Bird J. Electrical Circuit Theory and Technology
Подождите немного. Документ загружается.

928 Electrical Circuit Theory and Technology
(iv) Capacitor voltage, v
c
D L
1
CRV
CRs C 1
D CRVL
1
1
CR
s C
1
CR
D
CRV
CR
L
1
1
s C
1
CR
i.e., v
c
= Ve
.−t=CR/
as previously obtained in equation (45.8) on
page 905.
Problem 25. A series R –L circuit has a step input V applied to it.
Use Laplace transforms to determine an expression for the current
i flowing in the circuit given that when time t D 0, i D 0.
From Figure 45.6 and equation (45.11) on page 906,
v
R
C v
L
D V becomes iR C L
di
dt
D V
Using the procedure:
(i)
LfiRgCL
L
di
dt
D LfVg i.e., RLfigCL[sLfigi0] D
V
s
(ii) i0 D 0, hence R
LfigCLsLfigD
V
s
(iii) Rearranging gives: R C Ls
LfigD
V
s
i.e.,
LfigD
V
sR C Ls
(iv) i D
L
1
V
sR C Ls
Let
V
sR C Ls
A
s
C
B
R C Ls
D
AR C Ls C Bs
sR C Ls
Hence V D AR C Ls C Bs
When s D 0, V D AR from which, A D
V
R
When s D
R
L
, V D B
R
L
from which, B D
VL
R
Transients and Laplace transforms 929
Hence L
1
V
sR C Ls
D L
1
V/R
s
C
VL/R
R C Ls
D L
1
V
Rs
VL
RR C Ls
D L
1
V
R
1
s
V
R
1
R
L
C s
D
V
R
L
1
1
s
1
s C
R
L
Hence current,i =
V
R
.1
− e
−Rt=L
/ as previously obtained in equa-
tion (45.13), page 907.
Problem 26. If after a period of time, the switch in the R–L circuit
of Problem 25 is opened, use Laplace transforms to determine an
expression to represent the current transient response. Assume that
at the instant of opening the switch, the steady-state current flowing
is I.
From Figure 45.6, page 906, v
L
C v
R
D 0 when the switch is opened,
i.e., L
di
dt
C iR D 0
Using the procedure:
(i)
L
L
di
dt
C LfiRgDLf0g
i.e., L[s
Lfigi
0
] C RLfigD0
(ii) i
0
D I, hence L[sLfigI] C RLfigD0
(iii) Rearranging gives: Ls
LfigLI C RLfigD0
i.e., R C Ls
LfigDLI
and
LfigD
LI
R C Ls
(iv) Current, i D
L
1
LI
R C Ls
D LIL
1
1
L
R
L
C s
D
LI
L
L
1
1
s C
R
L

930 Electrical Circuit Theory and Technology
i.e., i = Ie
.−Rt=L/
from 3 of Table 45.1
Since I D
V
R
then i
=
V
R
e
−Rt
L
as previously derived in equation (45.17),
page 909.
Further problems on inverse Laplace transforms and the solution of
differential equations may be found in Section 45.10, problems 20 to 39,
page 954.
45.7 Laplace transform
analysis directly from the
circuit diagram
Resistor
At any instant in time
v D Ri
Since
v and i are both functions of time, a more correct equation would be
vt D Rit
However, this is normally assumed. The Laplace transform of this equa-
tion is:
Vs D RIs
Hence, in the s-domain Rs D
Vs
Is
D R
(Note that Vs merely means that it is the Laplace transform of
v and
Is is the Laplace transform of i. Whenever the Laplace transform of
functions is taken it is referred to as the ‘s-domain’ — as opposed to the
‘time domain’)
The resistor is shown in Figure 45.12 in both the time domain and the
s-domain.
R
v
i
Time
domain
+
−
R
V
(s)
I
(s)
+
−
s-domain
Figure 45.12
Inductor
If an inductor has no initial current, i.e., i D 0 at time t D 0, the normal
equation is
v D Ldi/dt where L is the inductance
The Laplace transform of the equation is:
Vs D L[sIs i0] from equation 45.33
and as i0 D 0 then Vs D sLIs
Thus the impedance of the inductor in the s-domain is given by:
Zs D
Vs
Is
D sL
The inductor is shown in Figure 45.13 in both the time domain and the
s-domain.
i
L
+−
v
Time
domain
I
(s)
sL
+−
V
(s)
s-domain
Figure 45.13
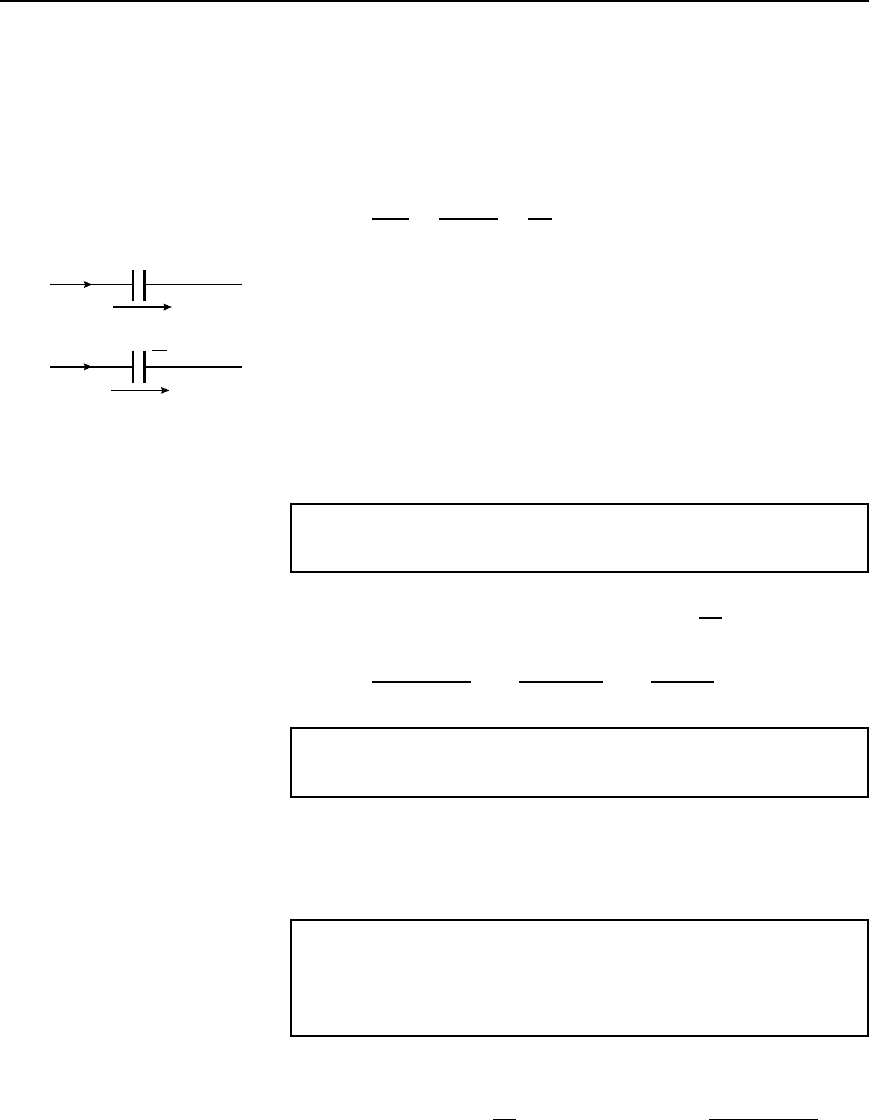
Capacitor
If a capacitor has no initial voltage, i.e.,
v D 0 at time t D 0, the normal
equation is i D Cd
v/dt
Transients and Laplace transforms 931
The Laplace transform of the equation is:
Is D C[sVs
v0]
D sC Vs since
v0 D 0
Thus the impedance of the capacitor in the s-domain is given by:
Zs D
Vs
Is
D
Vs
sCVs
D
1
sC
The capacitor is shown in Figure 45.14 in both the time domain and the
s-domain.
Summarising, in the time domain, the circuit elements are R, L and C
andinthes-domain, the circuit elements are R,sL and .1=sC/
Note that the impedance of L is X
L
D jωL and the impedance of C is
X
c
D j/ωC D 1/jωC
Thus, just replacing jω with s gives the s-domain expressions for L
and C. (Because of this apparent association with j, s is sometimes called
the complex frequency and the s-domain called the complex frequency
domain).
i
C
v
Time
domain
I
(s)
sC
V
(s)
s-domain
1
+−
+−
Figure 45.14
Problem 27. Determine the impedance of a 5 µF capacitor in the
s-domain
In the s-domain the impedance of a capacitor is
1
sC
hence
Zs D
1
s.5 × 10
−6
/
Z or
1
5 × 10
−6
s
Z or
2
× 10
5
s
Z
Problem 28. Determine the impedance of a 200 resistor in
series with an 8 mH inductor in the s-domain
The impedance of the resistor in the s-domain is 200
The impedance of the inductor in the s-domain is sL D 8 ð 10
3
s
Since the components are in series, Zs D .200 Y 8
× 10
−3
s/Z
Problem 29. A circuit comprises a 50 resistor, a 5 mH inductor
and a 0.04
µF capacitor. Determine, in the s-domain (a) the
impedance when the components are connected in series, and
(b) the admittance when the components are connected in parallel.
(a) R,L and C connected in series in the s-domain give an impedance,
Zs D R C sL C
1
sC
D
50 Y 5 × 10
−3
s Y
1
0.04 × 10
−6
s
Z
932 Electrical Circuit Theory and Technology
(b) R, L and C connected in parallel gives:
admittance Y D Y
1
C Y
2
C Y
3
D
1
Z
1
C
1
Z
2
C
1
Z
3
In the s-domain, admittance,
Ys D
1
R
C
1
sL
C
1
1
sC
D
1
R
C
1
sL
C sC
i.e., Y .s/
=
1
50
Y
1
5 × 10
−3
s
Y 0.04
× 10
−6
s
S
or Ys D
1
s
s
50
C
1
5 ð 10
3
C 0.04 ð 10
6
s
2
S
D
0.04 ð 10
6
s
s
500.04 ð 10
6
C
1
5 ð 10
3
0.04 ð 10
6
C s
2
S
i.e., Y .s/ D
4
× 10
−8
s
.s
2
Y 5 × 10
5
s Y 5 × 10
9
/S
Kirchhoff’s laws in the s-domain
Kirchhoff’s current and voltage laws may be applied to currents and volt-
ages in the s-domain just as they can with normal time domain currents
and voltages. To solve circuits in the s-domain using Kirchhoff’s laws the
procedure is:
(i) change the time domain circuit to an s-domain circuit,
(ii) apply Kirchhoff’s laws in terms of s,
(iii) solve the equation to obtain the Laplace transform of the unknown
quantity, and
(iv) determine the inverse Laplace transform after rearranging into a
form that can be recognised in a table of standard transforms.
This procedure is demonstrated in the following problems.
Problem 30. Determine an expression for (a) the current i through,
and (b) the voltage
v
c
across the capacitor for the circuit shown in
Figure 45.15, after the switch is closed with a supply step voltage
of V volts. Assume that the capacitor is initially uncharged.
R
i
v
C
C
V
Figure 45.15

Transients and Laplace transforms 933
R
v
C
(s)V
I(s)
sC
1
s
Figure 45.16
(a) Using the above procedure:
(i) In the s-domain the circuit impedance, Zs D R C 1/sC and
the step input voltage is V/s and the circuit is as shown in
Figure 45.16.
(ii) Applying Kirchhoff’s voltage law:
V
s
D RIs C
v
c
s 45.35
D RIs C
1
sC
Is
i.e.,
V
s
D Is
R C
1
sC
(iii) Rearranging gives:
Is D
V/s
R C
1
sC
D
V/s
R
1 C
1
RsC
D
V
sR
1 C
1
RsC
i.e., Is D
V
R
s C
1
RC
45.36
(iv) Hence current, i D
L
1
fIsgDL
1
V
R
s C
1
RC
D
V
R
L
1
1
s C
1
RC
since L
1
1
s a
D e
at
then L
1
1
s C a
D e
at
from 3
of Table 45.1. Hence
current, i
=
V
R
e
−.1=RC/t
=
V
R
e
−t=RC
as previously obtained in equation (45.6), page 903.
(b) From equation (45.35),
v
c
sD
V
s
RIs and from equation (45.36),
v
c
s D
V
s
R
V
R
s C
1
RC
D
V
s
V
s C
1
RC
D V
1
s
1
s C
1
RC
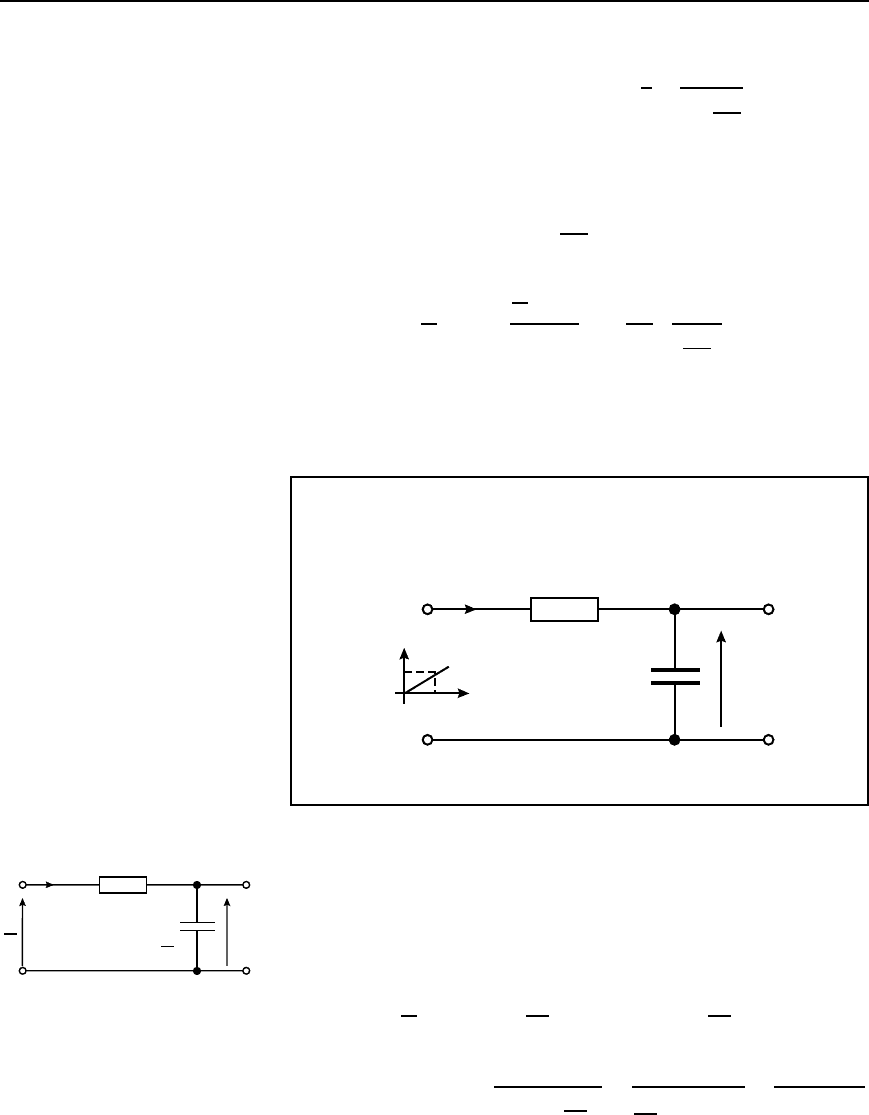
934 Electrical Circuit Theory and Technology
Hence v
c
D L
1
fv
c
sgDL
1
V
1
s
1
s C
1
RC
i.e., v
c
= V .1 − e
−t=RC
/ from 2 and 3 of Table 45.1,
as previously obtained in equation (45.4), page 903.
Alternatively, current, i D C
d
v
c
dt
, hence
v
c
D
t
0
i
C
dt D
t
0
V
R
e
t/RC
C
dt D
V
RC
e
t/RC
1
RC
t
0
DV[e
t/RC
]
t
0
DV[e
t/RC
e
0
] DV[e
t/RC
1]
i.e., V
c
= V .1 − e
−t=RC
/
Problem 31. In the R –C series circuit shown in Figure 45.17, a
ramp voltage V is applied to the input. Determine expressions for
(a) current, i, and (b) capacitor voltage,
v
c
i
R
V
V
C
t
C
v
C
1
Figure 45.17
(a) Using the procedure:
(i) The time domain circuit of Figure 45.17 is changed to the s-
domain as shown in Figure 45.18, where the ramp function is
V/s
2
from 7 of Table 45.1.
(ii) Applying Kirchhoff’s voltage law gives:
V
s
2
D RIs C
1
sC
Is D Is
R C
1
sC
(iii) Hence Is D
V
s
2
R C
1
sC
D
V
s
2
sC
RsC C 1
D
VC
s1 C sRC
I(s)
R
V
S
2
1
SC
vc(s)
Figure 45.18
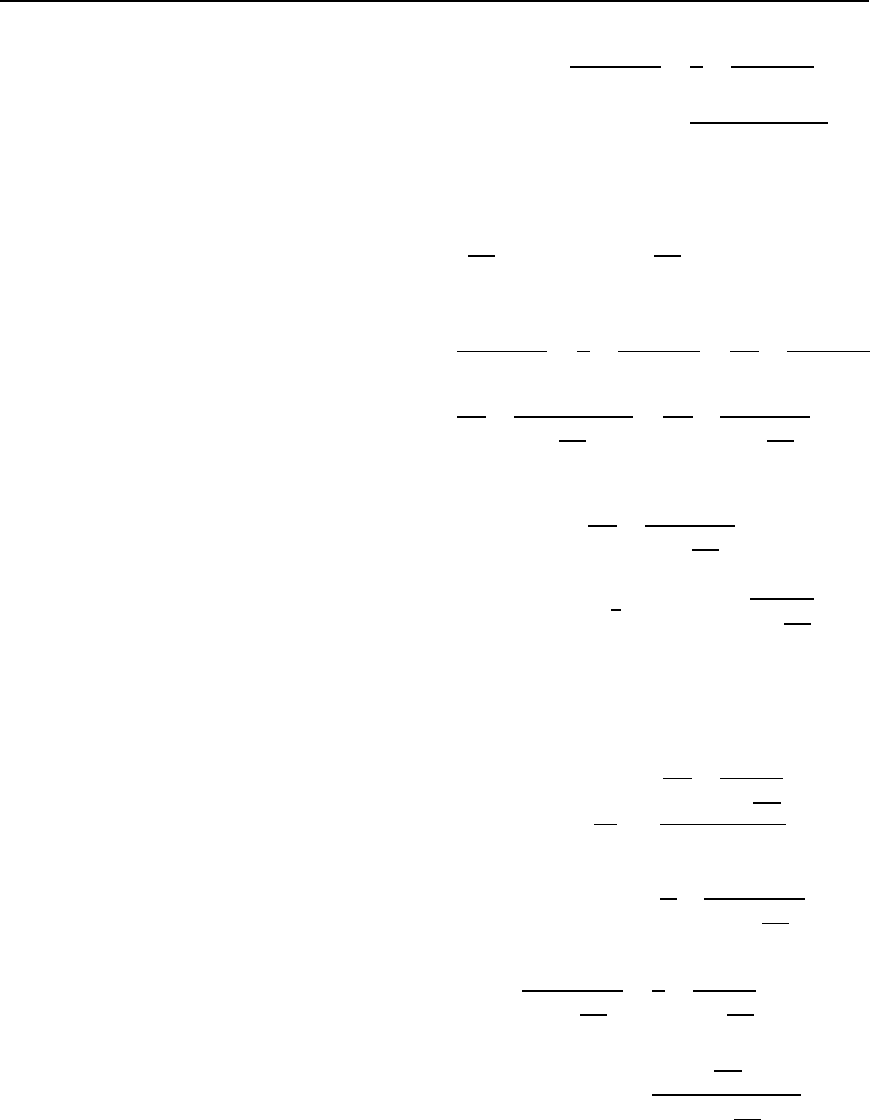
Transients and Laplace transforms 935
Using partial fractions:
VC
s1 C sRC
D
A
s
C
B
1 C sRC
D
A1 C sRC C Bs
s1 C sRC
Thus VC D A1 C sRC C Bs
When s D 0 VC D A C 0 i.e., A D VC
When s D
1
RC
VC D 0 C B
1
RC
i.e., B DVC
2
R
Hence
Is D
VC
s1 C sRC
D
A
s
C
B
1 C sRC
D
VC
s
C
VC
2
R
1 C sRC
D
VC
s
VC
2
R
RC
1
RC
C s
D
VC
s
VC
s C
1
RC
45.37
(iv) Current, i D
L
1
VC
s
VC
s C
1
RC
D VCL
1
1
s
VCL
1
1
s C
1
RC
D VC VCe
t/RC
from 2 and 3 of Table 45.1
i.e., current, i
= VC.1 − e
−t=RC
/
(b) Capacitor voltage,
v
c
s D Is
1
sC
D
VC
s
VC
s C
1
RC
sC
from equation (45.37)
D
V
s
2
V
s
s C
1
RC
Using partial fractions:
V
s
s C
1
RC
D
A
s
C
B
s C
1
RC
D
A
s C
1
RC
C Bs
s
s C
1
RC

936 Electrical Circuit Theory and Technology
hence V D A
s C
1
RC
C Bs
When s D 0
V D A
1
RC
C 0 from which, A D VCR
When s D
1
RC
V D 0 C B
1
RC
from which, B DVCR
Thus
v
c
s D
V
s
2
V
s
s C
1
RC
D
V
s
2
VCR
s
VCR
s C
1
RC
D
V
s
2
VCR
s
C
VCR
s C
1
RC
Thus, capacitor voltage,
v
c
D L
1
V
s
2
VCR
s
C
VCR
s C
1
RC
D Vt VCR C VCR e
t/RC
from7,2and3ofTable45.1
i.e.,
v
c
= Vt − VCR.1 − e
−t=RC
/
Rv
R
L
v
L
i
V
0
t
Figure 45.19
Problem 32. Determine for the R–L series circuit shown in
Figure 45.19 expressions for current i, inductor voltage
v
L
and
resistor voltage
v
R
when a step voltage V is applied to the input
terminals.
Using the procedure:
(i) The s-domain circuit is shown in Figure 45.20.
(ii) Using Kirchhoff’s voltage law:
V
s
D IssL C IsR
V
R
v
L
(
s
)
S
L
s
I
(s)
v
R
(
s
)
Figure 45.20
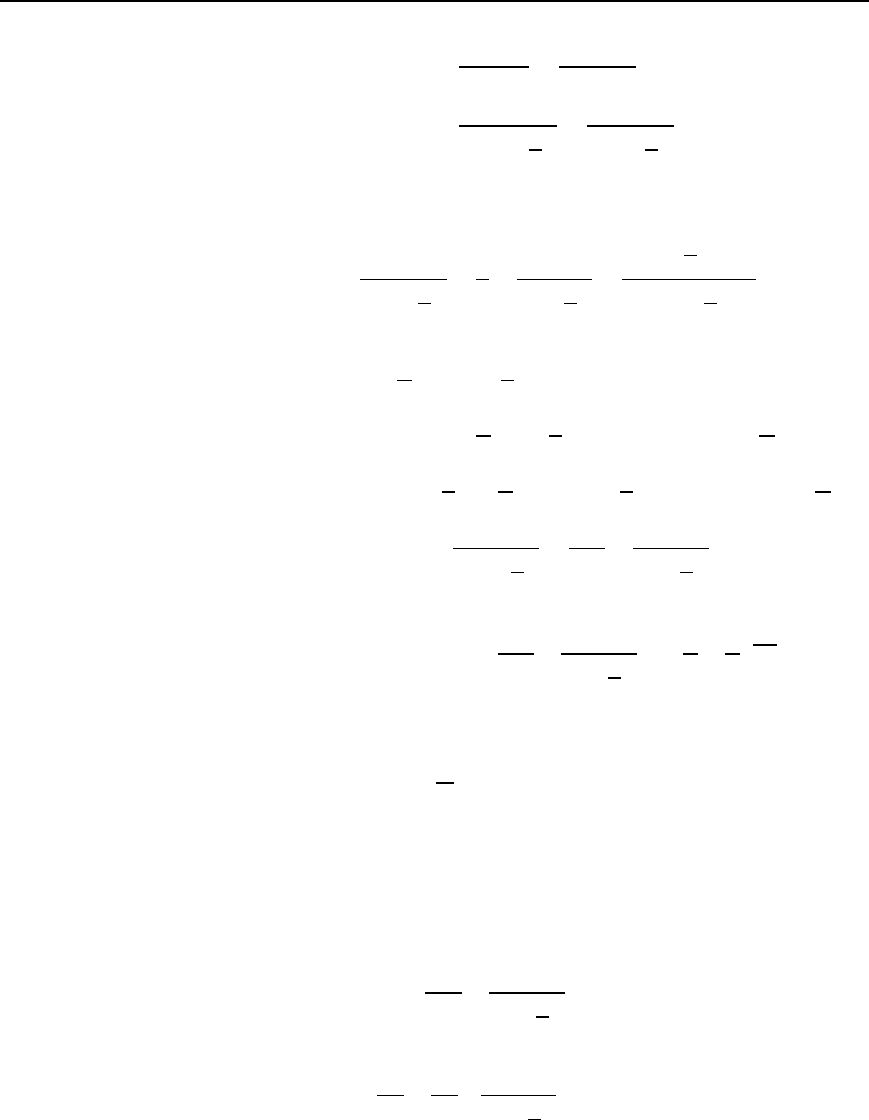
Transients and Laplace transforms 937
(iii) Current I(s) D
V/s
R C sL
D
V
sR C sL
D
V
sL
s C
R
L
D
V/L
s
s C
R
L
Using partial fractions:
V/L
s
s C
R
L
D
A
s
C
B
s C
R
L
D
A
s C
R
L
C Bs
s
s C
R
L
Hence
V
L
D A
s C
R
L
C Bs
When s D 0
V
L
D A
R
L
C 0 from which, A D
V
R
When s D
R
L
V
L
D 0 CB
R
L
from which, B D
V
R
Hence Is D
V/L
s
s C
R
L
D
V/R
s
V/R
s C
R
L
45.38
(iv) Current i D
L
1
V/R
s
V/R
s C
R
L
D
V
R
V
R
e
Rt
L
from 2 and 3 of Table 45.1
i.e., i
=
V
R
.1
− e
.−Rt=L/
/
as previously obtained in equation (45.13), page 907, and in
problem 25.
In the s-domain, inductor voltage
v
L
s D IssL
D sL
V/R
s
V/R
s C
R
L
from equation (45.38)
D
VL
R
VL
R
s
s C
R
L
