Bhushan B. Nanotribology and Nanomechanics: An Introduction

Подождите немного. Документ загружается.

192 Markus Morgenstern et al.

Intensity (photons/pC/meV)

1.2

1.4 1.6 1.8 2.0 2.2 2.4

Photon energy (eV)

1.5 2 2.5 3 3.5 4

Bias voltage (V)

Photon energy (eV)

= 2.57 V

= 2.27 V

= 2.13 V

= 2.05 V

= 2.03 V

= 1.91 V

= 1.83 V

hω= E

– E

ΔE = E

hω= eV

hω= E

– E

hω= eV – E

ΔE = E

a) b)

hω= eV – E

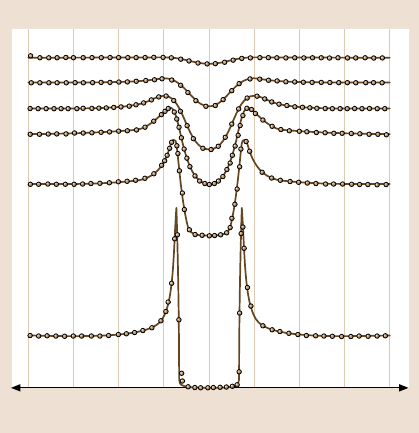
Fig. 5.7. (a)STMimage

of C

molecules on Au(110)

imaged atT = 50 K. (b)STM-

induced photon intensity map

of the same area; all pho-

tons from 1.5eVto2.8eV

contribute to the image, tun-

neling voltage V = −2.8V

((a),(b) courtesy of Berndt,

Kiel). (c) STM-induced pho-

ton spectrum measured on

0.6 monolayer of Na on

Cu(111) at diﬀerent tunnel-

ing voltages as indicated.

Besides the shifting plasmon

mode marked by an arrow,

an energetically constant

part named p is recogniz-

able. (d) Greyscale map of

photon intensity as a func-

tion of tunnelling voltage

and photon energy meas-

ured on 2.0 monolayer Na

on Cu(111). The energeti-

cally constant photons are

identiﬁed with intersubband

transitions of the Na quantum

well, as marked by E

−E

((c),(d) courtesy of Hoﬀ-

mann, Hamburg)

5 Low-Temperature Scanning Probe Microscopy 193

states are not only surface states, butalso bulkstates. However,surface states usually

dominate if present. Chen has shown that higher orbital tip states lead to the so-

called derivation rule [51]: p

-type tip states detect d(LDOS)/ dz,d

-states detect

(LDOS)/dz

, and so on. As long as the decay into vacuum is exponential and

spatially constant, this leads only to an additional factor in dI/ dV. Thus, it is still

the LDOS that is measured (5.1). The requirement of a spatially constant decay is

usually fulﬁlled on larger length scales, but not on the atomic scale [51]. There,

states located close to the atoms show a stronger decay into vacuum than the less

localized states in the interstitial region. This eﬀect can lead to corrugationsthat are

larger than the real LDOS corrugations[52].

The voltage dependence of dI/ dV is sensitive to a changing decay length

with V, which increaseswith V. Additionally, dI/ dV(V)-curvesmight be inﬂuenced

by possible structures in the DOS of the tip, which also contributes to the number

of tunneling channels [53]. However, these structures can usually be identiﬁed, and

only tips free of characteristic DOS structures are used for quantitativeexperiments.

Importantly, the energy resolution ΔE is largely determined by temperature. It is

deﬁned as the smallest energy distance of two δ-peaks in the LDOS that can still be

resolved as two individual peaks in dI/ dV(V)-curves and is ΔE = 3.3 kT [2]. The

temperature dependence is nicely demonstrated in Fig. 5.8, where the tunneling gap

of the superconductor Nb is measured at diﬀerent temperatures [54]. The peaks at

the rim of the gap get wider at temperatures well below the critical temperature of

the superconductor (T

= 9.2K).

Differential conductance (arb. units)

Sample bias (mV)

–8 –6 –4 –2 0 2 4 6 8

8.6 K

7.0 K

5.0 K

3.0 K

1.6 K

380 mK

Fig. 5.8. Diﬀerential conduc-

tivity curve dI/ dV(V) meas-

ured on a Au surface by a Nb

tip (circles). Diﬀerent temp-

eratures are indicated; the

lines are ﬁts according to the

superconducting gap of Nb

folded with the temperature-

broadened Fermi distribution

of the Au (courtesy of Pan,

Houston)

194 Markus Morgenstern et al.

Lifetime Broadening

Besides ΔE, intrinsic properties of the sample lead to a broadening of spectroscopic

features. Basically, the ﬁnite lifetime of the electron or hole in the corresponding

state broadens its energetic width. Any kind of interaction such as electron–electron

interaction can be responsible. Lifetime broadening has usually been measured by

photoemission spectroscopy (PES, but it turned out that lifetimes of surface states

on noble metal surfaces determined by STS (Fig. 5.9a,b) are up to a factor of three

largerthan those measured by PES [55].The reason is probably that defectsbroaden

the PESpectrum. Defects are unavoidable in a spatially integrating technique such

as PES thus, STS has the advantageof choosinga particularly clean area for lifetime

measurements. The STS results can be successfully compared to theory, highlight-

ing the dominating inﬂuence of intraband transitions for the surface-state lifetime

on Au(111) and Cu(111), at least close to the onset of the surface band [21].

With respect to band electrons, the analysis of the width of the band onset in

dI/ dV(V)-curves has the disadvantage of being restricted to the onset energy. An-

other method circumventsthis problemby measuring the decay of standing electron

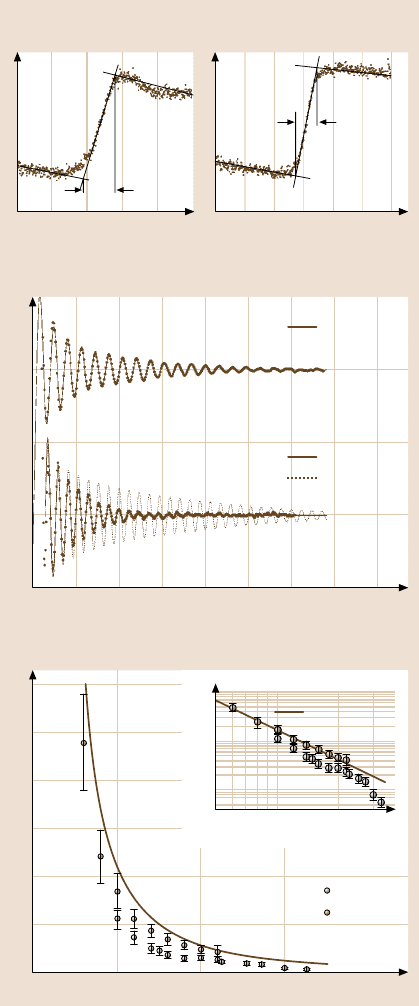
waves scattered from a step edge as a function of energy [56]. Figure 5.9c,d shows

the resulting oscillating dI/ dV-signal measured for two diﬀerent energies. To de-

duce the coherence length L

, which is inversely proportional to the lifetime τ

one has to consider that the ﬁnite ΔE in the experiment also leads to a decay of

the standing wave away from the step edge. The dotted ﬁt line using L

= ∞ in-

dicates this eﬀect and, more importantly, shows a discrepancy from the measured

curve.Only including a ﬁnite coherence length of 6.2nm results in goodagreement,

which, in turn, determines L

and thus τ

, as displayed in Fig. 5.9c. The found

1/E

-dependence of τ

points to a dominating inﬂuence of electron–electron inter-

actions at higher energies in the surface band.

Landau and Spin Levels

Moreover, the increased energy resolution at LT allows the resolution of electronic

states that are not resolvable at room temperature (RT). For example, Landau and

spin quantization appearingin a magnetic ﬁeld B havebeen probed on InAs(110)[9,

57]. The corresponding quantization energies are given by E

Landau

heB/m

eﬀ

and

spin

= gμB. Thus InAs is a good choice, since it exhibits a low eﬀective mass

eﬀ

= 0.023 and a high g-factor of 14 in the bulk conduction band. The values

in metals are m

eﬀ

≈ 1andg ≈ 2, resulting in energy splittings of only 1.25 meV

and 1.2meVatB = 10T. This is obviously lower than the typical lifetime broaden-

ings discussed in the previous section and also close to ΔE = 1.1meV achievable at

T = 4K.

Fortunately, the electron density in doped semiconductors is much lower, and

thus the lifetime increases signiﬁcantly. Figure 5.10a shows a set of spectroscopy

curves obtained on InAs(110) in diﬀerent magnetic ﬁelds [9]. Above E

, oscilla-

tions with increasing intensity and energy distance are observed. They show the

separation expected from Landau quantization. In turn, they can be used to deduce

5 Low-Temperature Scanning Probe Microscopy 195

dl/dV (arb. units)

Voltage (mV)

–50–70–90

dl/dV (arb. units)

Voltage (mV)

–500 –400 –300

dl/dV (arb. units)

x (Å)

0 50 100

150

(fs)

E – E

(eV)1

E – E

(eV)

0.5 1.0 2.0 3.0

100

∞ E – E

(eV)

8 mV

30 mV

E – E

= 1 eV

E – E

= 2 eV

= 178 Å

= 62 Å

= ∞

Cu(111)

a) b)

Ag(111)

Fig. 5.9. (a),(b) spatially av-

eraged dI/ dV(V)-curves of

Ag(111) and Cu(111); both

surfaces exhibit a surface

state with parabolic disper-

sion starting at −65 meV and

−430 meV, respectively. The

lines are drawn to determine

the energetic width of the

onset of these surface bands

((a),(b) courtesy of Berndt,

Kiel); (c)dI/ dV-intensity

as a function of position

away from a step edge of

Cu(111) measured at the volt-

ages (E −E

), as indicated

(points); the lines are ﬁts

assuming standing electron

waves with a phase coher-

ence length L

as marked;

(d) resulting phase coherence

time as a function of energy

for Ag(111) and Cu(111).

Inset shows the same data on

a double logarithmic scale ev-

idencing the E

−2

-dependence

(line)((c),(d) courtesy of

Brune, Lausanne)

196 Markus Morgenstern et al.

V (arb. units)

–40 0 120

6 T

40 80

5 T

4 T

3 T

2 T

1 T

Sample voltage (mV)

eff

– E

(meV)

0 50 300

0.06

0.05

0.04

0.03

0.02

0.01

100 150 200 250

V (arb. units)

Sample voltage (mV)

10 20 30 40 50 60 70

BCBM

2.5 T – 6.0 T

Tsui (1971)

kp-theory

LL1

LL2

Exp.

Fit

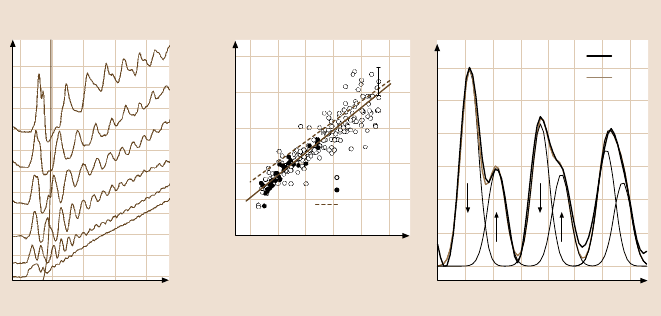
Fig. 5.10. (a)dI/ dV-curves of n-InAs(110) at diﬀerent magnetic ﬁelds as indicated; E

BCBM

marks the bulk conduction band minimum; oscillations above E

BCBM

are caused by Landau

quantization; the double peaks at B = 6 T are caused by spin quantization. (b)Eﬀective-mass

data deduced from the distance of adjacent Landau peaks ΔE according to ΔE = heB/m

eﬀ

(open symbols); ﬁlled symbols are data from planar tunnel junctions (Tsui), the solid line is

amean-sqareﬁtofthedataandthedashed line is the expected eﬀective mass of InAs accord-

ing to kp-theory. (c)MagniﬁcationofadI/ dV-curve at B = 6 T exhibiting spin splitting; the

Gaussian curves marked by arrows are the ﬁtted spin levels

eﬀ

from the peak separation (Fig. 5.10b). An increase of m

eﬀ

with increasing E

has been found, as expected from theory. Also, at high ﬁelds spin quantization is

observed (Fig. 5.10c). It is larger than expected from the bare g-factor due to con-

tributions from exchange enhancement [58]. A detailed discussion of the peaks re-

vealed that they belong to the so-called tip-induced quantum dot resulting from the

work function diﬀerence between the tip and sample.

Vibrational Levels

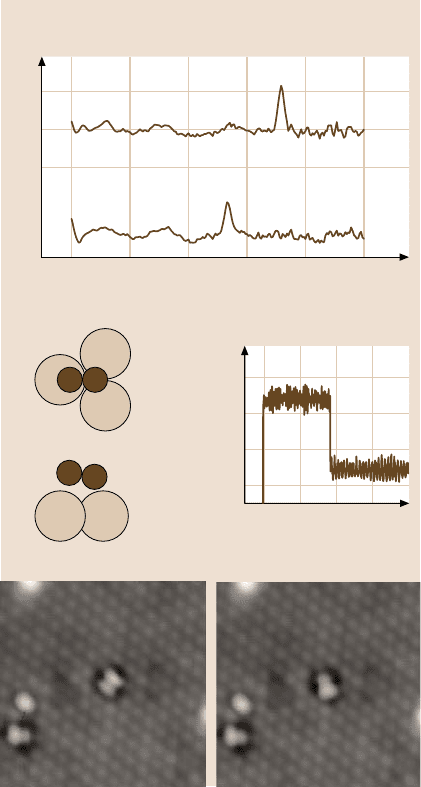
As discussed with respect to light emission in STM, inelastic tunneling processes

contribute to the tunneling current. The coupling of electronic states to vibrational

levels is one source of inelastic tunneling [23]. It provides additional channels con-

tributing to dI/ dV(V) with ﬁnal states at energies diﬀerent from V. The ﬁnal energy

is simply shifted by the energy of the vibrational level. If only discrete vibrational

energy levels couple to a smooth electronic DOS, one expects a peak in d

I/ dV

at the vibrational energy. This situation appears for molecules on noble-metal sur-

faces. As usual, the isotope eﬀect on the vibrational energy can be used to verify

the vibrational origin of the peak. First indications of vibrational levels have been

found for H

OandD

OonTiO

[59], and completely convincing work has been

performed for C

and C

on Cu(001) [23] (Fig. 5.11a). The technique can be

used to identify individual molecules on the surface by their characteristic vibra-

tional levels. In particular, surface reactions, as described in Fig. 5.5h–m, can be

directly veriﬁed. Moreover, the orientation of complexes with respect to the surface

5 Low-Temperature Scanning Probe Microscopy 197

l/dV

(nA/V

)

Voltage (mV)

–20

100 200 300 400 500

I (nA)

10 20 30

Time (ms)

0.15 Volt pulse

358

266

b) c)

Top

Side

d) e)

Fig. 5.11. (a)d

I/ dV

curves taken above a C

and a C

molecule on

Cu(100); the peaks corre-

spond to the C

−

H, respec-

tively, C

−

D stretch-mode

energy of the molecule.

(b)SketchofO

molecule

on Pt(111). (c) Tunnelling

current above an O

molecule

on Pt(111) during a voltage

pulse of 0.15 V; the jump in

current indicates rotation of

the molecule. (d), (e)STM

image of an O

molecule on

Pt(111) (V = 0.05 V) prior

and after rotation induced

by a voltage pulse to 0.15 V

((a)–(e) courtesy of Ho,

Irvine)

can be determined to a certain extent, since the vibrational excitation depends on

the position of the tunneling current within the molecule. Finally, the excitation of

certain molecular levels can induce such corresponding motions as hopping [32],

rotation [34] (Fig. 5.11b–e), or desorption [31], leading to additional possibilities

for manipulation on the atomic scale.

Kondo Resonance

A rather intricate interaction eﬀect is the Kondo eﬀect. It results from a second-

order scattering process between itinerate states and a localized state [60]. The two

states exchange some degree of freedom back and forth, leading to a divergence of

198 Markus Morgenstern et al.

the scattering probability at the Fermi level of the itinerate states. Due to the di-

vergence, the eﬀect strongly modiﬁes sample properties. For example, it leads to an

unexpectedincrease in resistance with decreasing temperaturefor metals containing

magnetic impurities [4]. Here, the exchanged degree of freedom is the spin. A spec-

troscopic signature of the Kondo eﬀect is a narrow peak in the DOS at the Fermi

level,disappearingabovea characteristictemperature(the Kondotemperature).STS

provides the opportunity to study this eﬀect on the local scale [61,62].

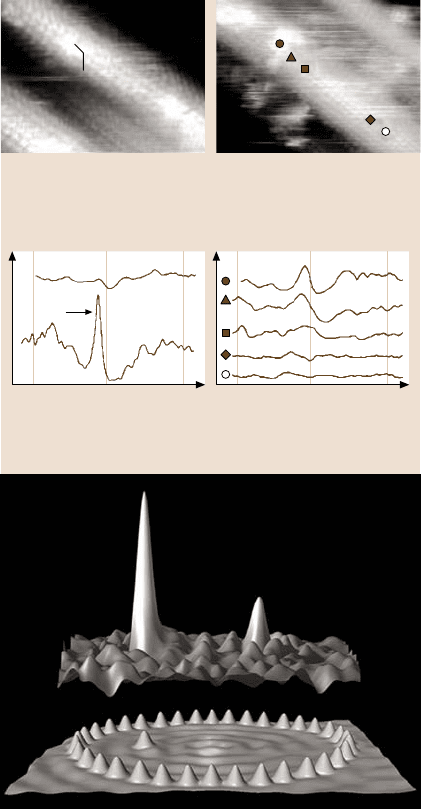
Figure 5.12a–d shows an example of Co clusters deposited on a carbon nano-

tube [63]. While a small dip at the Fermi level, which is probably caused by curva-

dl/dV (arb. units)

bias voltage (V)

–0.2 0 0.2

dl/dV (arb. units)

bias voltage (V)

–0.2 0 0.2

SWNT

a) c)

b) d)

Fig. 5.12. (a)STMimageof

a Co cluster on a single-wall

carbon nanotube (SWNT).

(b)dI/ dV-curves taken di-

rectly above the Co cluster

(Co) and far away from the

Co cluster (SWNT); the ar-

row marks the Kondo peak.

cluster on a SWNT with sym-

bols marking the positions

where the dI/ dV-curves

displayed in (d)aretaken.

(d)dI/ dV-curves taken at

the positions marked in (c)

((a)–(d) courtesy of Lieber,

Cambridge). (e) Lower part:

STM image of a quantum

corral of elliptic shape made

from Co atoms on Cu(111);

one Co atom is placed in one

of the foci of the ellipse. Up-

per part: map of the strength

of the Kondo signal in the

corral; note that there is also

a Kondo signal in the focus,

whichisnotcoveredbyaCo

atom ((e) courtesy of Eigler,

Almaden)

5 Low-Temperature Scanning Probe Microscopy 199

ture inﬂuences on the π-orbitals, is observed without Co (Fig. 5.12b) [64], a strong

peak is found around a Co cluster deposited on top of the tube (Fig. 5.12a, arrow).

The peak is slightly shifted with respect to V = 0 mV due to the so-called Fano res-

onance [65], which results from interference of the tunneling processes into the lo-

calized Co-level and the itinerant nanotube levels. The resonance disappears within

several nanometers of the cluster, as shown in Fig. 5.12d.

The Kondo eﬀect has also been detected for diﬀerent magnetic atoms deposited

on noble-metal surfaces [61,62]. There, it disappears at about 1nm from the mag-

netic impurity, and the eﬀect of the Fano resonance is more pronounced, contribut-

ingtodipsindI/ dV(V)-curves instead of peaks.

A fascinating experiment has been performed by Manoharan et al. [66],

who used manipulation to form an elliptic cage for the surface states of Cu(111)

(Fig. 5.12e, bottom). This cage was constructed to have a quantized level at E

Then, a cobalt atom was placed in one focus of the elliptic cage, producing a Kondo

resonance. Surprisingly, the same resonance reappeared in the opposite focus, but

not away from the focus (Fig. 5.12e, top). This shows amazingly that complex local

eﬀects such as the Kondo resonance can be guided to remote points.

Orbitalscatteringas asourceof the Kondoresonance hasalso beenfoundaround

a defect on Cr(001) [67]. Here, it is believed that itinerate sp-levels scatter at a lo-

calized d-level to produce the Kondo peak.

5.4.5 Imaging Electronic Wave Functions

Since STS measuresthe sum of squared wave functions(5.1), it is an obvioustask to

measure the local appearance of the most simple wave functions in solids, namely,

Bloch waves.

Bloch Waves

The atomically periodicpart of the Bloch wave is always measured if atomicresolu-

tion isachieved (inset ofFig. 5.14a). However,the long-rangewavy partrequires the

presence of scatterers. The electron wave impinges on the scatterer and is reﬂected,

leading to self-interference. In other words, the phase of the Bloch wave becomes

ﬁxed by the scatterer.

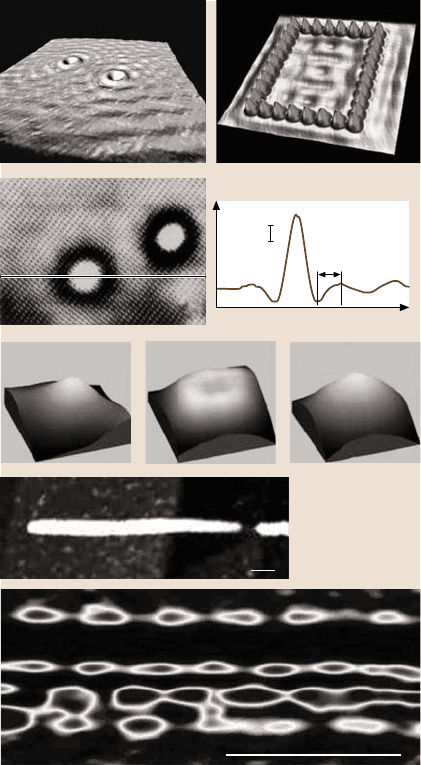
Such self-interferencepatterns were ﬁrst found on Graphite(0001)[68] and later

on noble-metal surfaces, where adsorbates or step edges scatter the surface states

(Fig. 5.13a) [22]. Fourier transforms of the real-space images reveal the k-space

distribution of the corresponding states [69], which may include additional contri-

butions besides the surface state [70]. Using particular geometries as the so-called

quantum corrals to form a cage for the electron wave, the scattering state can be

rather complex (Fig. 5.13b). Anyway, it can usually be reproduced by simple calcu-

lations involving single-particle states [71].

Bloch waves in semiconductors scattered at charged dopants(Fig. 5.13c,d) [72],

Blochstates conﬁnedin semiconductorquantumdots (Fig.5.13e–g)[73], andBloch

waves conﬁned in short-cut carbon nanotubes (Fig. 5.13h,i) [74,75] have been vi-

sualized.

200 Markus Morgenstern et al.

Height

10 nm

1 nm

Distance

25Å

0.2Å

a) b)

e) f) g)

= 0.9 V V

= 1.4 V V

= 1.9 V

Fig. 5.13. (a) Low-voltage STM image of Cu(111), including two defect atoms; the waves

are electronic Bloch waves scattered at the defects. (b) Low-voltage STM image of a rectan-

gular quantum corral made from single atoms on Cu(111); the pattern inside the corral is the

conﬁned state of the corral close to E

;((a),(b) courtesy of Eigler, Almaden). (c)STMimage

of GaAs(110) around a Si donor, V = −2.5 V; the line scan along A shown in (d) exhibits an

additional oscillation around the donor caused by a standing Bloch wave; the grid like pattern

corresponds to the atomic corrugation of the Bloch wave ((c),(d) courtesy of van Kempen,

Nijmegen). (e)–(g) STM images of an InAs/ZnSe-core/shell-nanocluster at diﬀerent V.The

image is measured in the so-called constant-height mode, i.e., the images display the tun-

neling current at constant height above the surface; the hill in (e) corresponds to the s-state

of the cluster, the ring in (f) to the degenerate p

-andp

-state and the hill in (g)tothep

state ((e)–(g) courtesy of Millo, Jerusalem). (h) STM-image of a short-cut carbon nanotube.

(i) Colour plot of the dI/ dV intensity inside the short-cut nanotube as a function of position

and tunneling voltage; four wavy patterns of diﬀerent wavelength are visible in the voltage

range from −0.1to0.15 V ((h),(i) courtesy of Dekker, Delft)

5 Low-Temperature Scanning Probe Microscopy 201

100 nm 100 nm

5Å

a) c)

b) d)

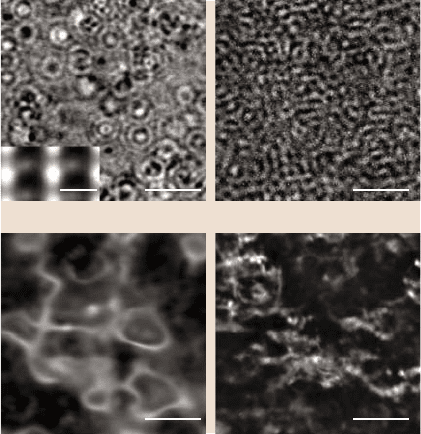
Fig. 5.14. (a)dI/ dV-image

of InAs(110) at V = 50 mV,

B = 0 T; circular wave pat-

terns corresponding to stand-

ing Bloch waves around

each S donor are visible;

inset shows a magniﬁca-

tion revealing the atomically

periodic part of the Bloch

wave. (b)Sameas(a), but at

B = 6 T; the stripe structures

are drift states. (c)dI/ dV-

image of a 2-D electron sys-

tem on InAs(110) induced by

the deposition of Fe, B = 0T.

(d)Sameas(c)butatB = 6T;

note that the contrast in (a)is

increased by a factor of ten

with respect to (b)–(d)

Drift States

More-complex wave functions result from interactions. A nice playground to study

such interactions is doped semiconductors. The reduced electron density with re-

spect to metals increases the importance of electron interactionswith potentialdisor-

der and other electrons. Applying a magnetic ﬁeld quenches the kinetic energy, fur-

ther enhancing the importance of interactions. A dramatic eﬀect can be observed on

InAs(110),where three-dimensional(3-D)bulkstates are displayed.While the usual

scattering states around individualdopants are observedat B = 0T (Fig. 5.14a) [76],

stripe structures are found in high magnetic ﬁeld (Fig. 5.14b) [77]. They run along

equipotentiallines of the disorderpotential. This can be understood by recalling that

the electron tries to move in a cyclotron orbit, which is accelerated and decelerated

in electrostatic potential, leading to a drift motion along an equipotential line [78].

Thesameeﬀect has been found in two-dimensional (2-D) electron systems (2-

DES) of the same substrate, where the scattering states at B = 0 T are, however,

found to be more complex (Fig. 5.14c) [79]. The reason is the tendency of a 2-DES

to exhibit closed scattering paths [80]. Consequently, the self-interference does not

resultfrom scatteringat individualscatterers,butfrom complicatedself-interference

paths involving many scatterers. However, drift states are also observed in the 2-

DES at high magnetic ﬁelds (Fig. 5.14d) [81].

Charge Density Waves

Another interaction modifying the LDOS is the electron–phonon interaction. Pho-

nons scatter electrons between diﬀerent Fermi points. If the wave vectors connect-

ing Fermi points exhibit a preferential orientation, a so-called Peierls instability oc-