Bhushan B. Nanotribology and Nanomechanics: An Introduction

Подождите немного. Документ загружается.

202 Markus Morgenstern et al.

TCNQ TTF

log I

Distance (nm)

012345678

d)a)

TCNQ TTF

e) f) g)

Fig. 5.15. (a) STM image of the ab-plane of the organic quasi-1-D conductor TTF-TCNQ,

T = 300 K; while the TCNQ chains are conducting, the TTF chains are insulating. (b) Stick-

and-ball model of the ab-plane of TTF-TCNQ. (c) STM image taken at T = 61 K, the ad-

ditional modulation due to the Peierls transition is visible in the proﬁle along line A shown

in (d); the brown triangles mark the atomic periodicity and the black triangles the expected

CDW periodicity ((a)–(d) courtesy of Kageshima, Kanagawa). (e)–(h) Low-voltage STM

images of the two-dimensional CDW-system 1T-TaS

at T = 242 K (e), 298 K (f), 349 K (g),

357 K (h). A long-range, hexagonal modulation is visible besides the atomic spots; its perio-

dicity is highlighted by large white dots in (e); the additional modulation obviously weakens

with increasing T, but is still apparent in (f)and(g), as evidenced in the lower magniﬁcation

images in the insets ((e)–(h) courtesy of Lieber, Cambridge)

curs [82]. The corresponding phonon energy goes to zero, the atoms are slightly

displaced with the periodicity of the corresponding wave vector, and a charge den-

sity wave (CDW) with the same periodicity appears. Essentially, the CDW increases

the overlap of the electronic states with the phonon by phase-ﬁxing with respect to

the atomic lattice. The Peierls transition naturally occurs in one-dimensional (1-D)

systems, where only two Fermi points are present, and, hence, preferential orienta-

tion is pathological. It can also occur in 2-D systems if large areas of the Fermi line

runinparallel.

STS studies of CDWs are numerous (e.g., [83,84]). Examples of a 1-D CDW

on a quasi-1-D bulk material and of a 2-D CDW are shown in Fig. 5.15a–d and

Fig. 5.15e, respectively [85,86]. In contrast to usual scattering states, where LDOS

corrugationsare onlyfound close to thescatterer,the corrugationsof CDWs are con-

tinuous across the surface. Heating the substrate toward the transition temperature

leads to a melting of the CDW lattice, as shown in Fig. 5.15f–h.

CDWs have also been found on monolayers of adsorbates such as a monolayer

of Pbon Ge(111)[87].These authorsperformeda nicetemperature-dependentstudy

revealingthatthe CDWis nucleatedby scatteringstates arounddefects,as one might

expect [88]. 1-D systems have also been prepared on surfaces showing Peierls tran-

5 Low-Temperature Scanning Probe Microscopy 203

sitions [89,90]. Finally, the energy gap occurring at the transition has been studied

by measuring dI/ dV(V)-curves [91].

Superconductors

An intriguing eﬀect resulting from electron–phonon interaction is superconductiv-

ity. Here, the attractive part of the electron–phononinteraction leads to the coupling

of electronic states with opposite wave vector and mostly opposite spin [92]. Since

the resulting Cooper pairs are bosons, they can condense at LT, forming a coher-

ent many-particle phase, which can carry current without resistance. Interestingly,

defect scattering does not inﬂuence the condensate if the coupling along the Fermi

surface is homogeneous (s-wave superconductor). The reason is that the symmetry

of the scattering of the two components of a Cooper pair eﬀectively leads to a scat-

tering from one Cooper pair state to another without aﬀecting the condensate. This

is diﬀerent if the scatterer is magnetic, since the diﬀerent spin components of the

pair are scattered diﬀerently, leading to an eﬀective pair breaking, which is visible

as a single-particle excitation within the superconducting gap. On a local scale, this

eﬀect was ﬁrst demonstrated by putting Mn, Gd, and Ag atoms on a Nb(110) sur-

face [93]. While the nonmagnetic Ag does not modify the gap shown in Fig. 5.16a,

it is modiﬁed in an asymmetric fashion close to Mn or Gd adsorbates, as shown in

Fig. 5.16b. The asymmetry of the additional intensity is caused by the breaking of

the particle–hole symmetry due to the exchange interaction between the localized

Mn state and the itinerate Nb states.

Another important local eﬀect is caused by the relatively large coherence length

of the condensate. At a material interface, the condensate wave function cannot

stop abruptly, but overlaps into the surrounding material (proximity eﬀect). Conse-

quently, a superconducting gap can be measured in areas of non-superconducting

material. Several studies have shown this eﬀect on the local scale using metals and

doped semiconductors as surrounding materials [94,95].

While the classical type-I superconductors are ideal diamagnets, the so-called

type-II superconductors can contain magnetic ﬂux. The ﬂux forms vortices, each

containing one ﬂux quantum. These vortices are accompanied by the disappearance

of the superconducting gap and, therefore, can be probed by STS [96]. LDOS maps

measured inside the gap lead to bright features in the area of the vortex core. Im-

portantly, the length scale of these features is diﬀerent from the length scale of the

magnetic ﬂux due to the diﬀerence between London’s penetration depth and the

coherence length. Thus, STS probes another property of the vortex than the usual

magnetic imaging techniques (see Sect. 5.5.4). Surprisingly, ﬁrst measurements of

the vortices on NbSe

revealed vortices shaped as a sixfold star [97] (Fig. 5.16c).

With increasing voltage inside the gap, the orientation of the star rotates by 30

◦

(Fig. 5.16d,e). The shape of these stars could ﬁnally be reproduced by theory, as-

sumingan anisotropicpairingof electronsin the superconductor(Fig. 5.16f–h) [98].

Additionally, bound states inside the vortex core, which result from conﬁnement

by the surrounding superconducting material, are found [97]. Further experiments

investigated the arrangement of the vortex lattice, including transitions between

204 Markus Morgenstern et al.

a) b)

c) d) e) f) g) h)

j) k)

dl/dV (10

–7

–1

)

(Volt)

–0.008 –0.004

1.2

0.8

0.4

0 0.004 0.008

dl/dV difference (10

–7

–1

)

Voltage (mV)

–4

0.4

0.2

–0.2

8–8 0 4

0–50 –50

3.0

2.6

2.2

1.8

1.4

1.0

0.6

0.2

Voltage (mV)

2 pA

0 pA

100 Å

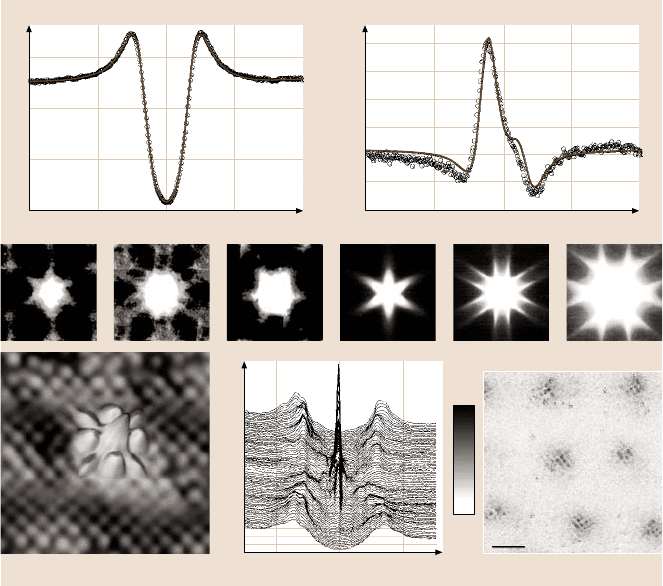
Fig. 5.16. (a)dI/ dV-curve of Nb(110) atT = 3.8K(symbols) in comparison with aBCS ﬁt of

the superconducting gap of Nb (line). (b)Diﬀerence between the dI/ dV-curve taken directly

above a Mn-atom on Nb(110) and the dI/ dV-curve taken above the clean Nb(110) (symbols)

in comparison with a ﬁt using the Bogulubov-de Gennes equations (line)((a),(b) courtesy

of Eigler, Almaden). (c)–(e)dI/ dV-images of a vortex core in the type-II superconduc-

tor 2H-NbSe

at 0 mV (c), 0.24 mV (d), and 0.48 mV (e)((c)–(e) courtesy of H.F. Hess).

(f)–(h) Corresponding calculated LDOS images within the Eilenberger framework ((f)–

(h) courtesy of Machida, Okayama). (i) Overlap of an STM image at V = −100 mV (back-

ground 2-D image) and a dI/dV-image at V = 0 mV (overlapped 3-D image) of optimally

doped Bi

CaCu

8+δ

containing 0.6% Zn impurities. The STM image shows the atomic

structure of the cleavage plane, while the dI/ dV-image shows a bound state within the su-

perconducting gap, which is located around a single Zn impurity. The fourfold symmetry

of the bound state reﬂects the d-like symmetry of the superconducting pairing function;

(j)dI/dV-curves taken at diﬀerent positions across the Zn impurity; the bound state close

to 0 mV is visible close to the Zn atom; (k) LDOS in the vortex core of slightly over-

doped Bi

CaCu

8+δ

, B = 5T; the dI/ dV-image taken at B = 5 T is integrated over

V = 1−12 mV, and the corresponding dI/ dV-image at B = 0 T is subtracted to highlight the

LDOS induced by the magnetic ﬁeld. The checkerboard pattern within the seven vortex cores

exhibits a periodicity, which is fourfold with respect to the atomic lattice shown in (i)andis

thus assumed to be a CDW ((i)–(k) courtesy of S. Davis, Cornell and S. Uchida, Tokyo)

5 Low-Temperature Scanning Probe Microscopy 205

hexagonal and quadratic lattices [99], the inﬂuence of pinning centers [100], and

the vortex motion induced by current [101].

The understandingof high-temperaturesuperconductivity(HTCS) is still an im-

portant topic. An almost accepted property of HTCS is its d-wave pairing sym-

metry. In contrast to s-wave superconductors, scattering can lead to pair breaking,

since the Cooper-pairdensity vanishesin certain directions. Indeed,scattering states

(bound states in the gap) around nonmagnetic Zn impurities have been observed in

CaCu

8+δ

(BSCCO) (Fig. 5.16i,j) [26]. They reveal a d-like symmetry, but

not the one expectedfrom simple Cooper-pairscattering. Other eﬀects such as mag-

netic polarization in the environment probably have to be taken into account [102].

Moreover, it has been found that magnetic Ni impurities exhibit a weaker scatter-

ing structure than Zn impurities [103]. Thus, BSCCO shows exactly the opposite

behavior to that of Nb discussed above(Fig. 5.16a,b). An interesting topic is the im-

portance of inhomogeneities in HTCS materials. Evidence for inhomogeneities has

indeed been found in underdoped materials, where puddles of the superconducting

phase are shown to be embedded in non-superconductingareas [104].

Of course, vortices have also been investigated in HTCS materials [105]. Bound

states are found,but at energiesthat are in disagreement with simple models,assum-

ing a Bardeen–Cooper–Schrieﬀer (BCS)-like d-wave superconductor [106, 107].

Theory predicts, instead, that the bound states are magnetic-ﬁeld-inducedspin den-

sity waves, stressing the competition between antiferromagnetic order and super-

conductivity in HTCS materials [108]. Since the spin density wave is accompanied

by a charge density wave of half wavelength, it can be probed by STS [109]. In-

deed, a checkerboard pattern of the right periodicity has been found in and around

vortex cores in BSCCO (Fig. 5.16k). It exceeds the width of an individual vortex

core, implying that the superconductingcoherence length is diﬀerent from the anti-

ferromagnetic one.

Complex Systems (Manganites)

Complex phase diagrams are not restricted to HTCS materials (cuprates). They ex-

ist with similar complexity for other doped oxides such as manganites. Only a few

studies of these materials have been performed by STS, mainly showing the inho-

mogeneousevolutionof metallic and insulating phases[110,111].Similarities to the

granular case of an underdopedHTCS material are obvious. Since inhomogeneities

seem to be crucial in many of these materials, a local method such as STS might

continue to be important for the understanding of their complex properties.

5.4.6 Imaging Spin Polarization: Nanomagnetism

Conventional STS couples to the LDOS, i.e., the charge distribution of the elec-

tronic states. Since electrons also have spin, it is desirable to also probe the spin

distribution of the states. This can be achieved if the tunneling tip is covered by

a ferromagnetic material [112]. The coating acts as a spin ﬁlter or, more precisely,

the tunneling current depends on the relative angle α

between the spins of the tip

206 Markus Morgenstern et al.



Fig. 5.17. (a)–(d) Spin-polarized STM images of 1.65 monolayer of Fe deposited on

a stepped W(110) surface measured at diﬀerent B-ﬁelds, as indicated. Double-layer and

monolayer Fe stripes are formed on the W substrate; only the double-layer stripes exhibit

magnetic contrast with an out-of-plane sensitive tip, as used here. White and grey areas corre-

spond to diﬀerent domains. Note that more white areas appear with increasing ﬁeld. (e)STM

image of an antiferromagnetic Mn monolayer on W(110). (f) Spin-polarized STM-image of

the same surface (in-plane tip). The insets in (e)and(f) show the calculated STM and spin-

polarized STM images, respectively, and the stick-and-ball models symbolize the atomic and

the magnetic unit cell ((a)–(f) courtesy of M. Bode, Hamburg). (g) Spin-polarized STM im-

age of a 6-nm-high Fe island on W(110) (in-plane tip). Four diﬀerent areas are identiﬁed

as four diﬀerent domains with domain orientations, as indicated by the arrows.(h) Spin-

polarized STM image of the central area of an island; the size of the area is indicated by the

rectangle in (g); the measurement is performed with an out-of-plane sensitive tip showing

that the magnetization turns out-of-plane in the center of the island

and the sample according to cos(α

). In ferromagnets, the spins mostly have one

preferential orientation along the so-called easy axis, i.e., a particular tip is not sen-

sitive to spin orientationsof the sample that are perpendicularto the spin orientation

of the tip. Diﬀerent tips have to be prepared to detect diﬀerent spin orientations of

the sample. Moreover, the magnetic stray ﬁeld of the tip can perturb the spin orien-

tation of the sample. To avoidthis, a technique using antiferromagnetic Cr as a tip

coating material has been developed [113]. This avoids stray ﬁelds, but still pro-

vides a preferential spin orientation of the few atoms at the tip apex that dominate

the tunneling current. Depending on the thickness of the Cr coating, spin orienta-

tions perpendicular or parallel to the sample surface are prepared.

So far,the described techniquehas been used to image the evolution of magnetic

domains with increasing B-ﬁeld (Fig. 5.17a–d) [114], the antiferromagnetic order

of a Mn monolayer on W(110) (Fig. 5.17e,f) [115], and the out-of-plane orientation

predicted for a magnetic vortexcore as it exists in the center of a Fe island exhibiting

four domains in the ﬂux closure conﬁguration (Fig. 5.17g,h) [116].

Besides the obvious strong impact on nanomagnetism,the technique might also

be usedto investigateother electronicphases suchas the proposedspin densitywave

around a HTCS vortex core.

5.5 Scanning Force Microscopy and Spectroscopy

The examples discussed in the previous section show the wide variety of physical

questions that have been tackled with the help of LT-STM. Here, we turn to the

other prominent scanningprobe method that is applied at low temperatures,namely,

SFM, which gives complementary information on sample properties on the atomic

scale.

5 Low-Temperature Scanning Probe Microscopy 207

400 mT

300 mT

200 mT

0 mT

50 nm

15 nm

Theory

Experiment

Theory

Experiment

[001]

10]

150 nm

208 Markus Morgenstern et al.

The ability to detect forces sensitively with spatial resolution downto the atomic

scale is of great interest, since force is one of the most fundamental quantities in

physics. Mechanical force probes usually consist of a cantilever with a tip at its

free end that is brought close to the sample surface. The cantilever can be mounted

parallel or perpendicular to the surface (general aspects of force probe designs are

described in Chap. 3). Basically, two methods exist to detect forces with cantilever-

based probes: the static and the dynamic mode (see Chap. 2). They can be used

to generate a laterally resolved image (microscopy mode) or determine its distance

dependence (spectroscopy mode).One can argue about the terminology, since spec-

troscopy is usually related to energies and not to distance dependencies. Neverthe-

less, we will use it throughout the text, because it avoids lengthy paraphrases and is

established in this sense throughout the literature.

In the static mode, a force that acts on the tip bends the cantilever. By measuring

its deﬂection Δz the tip–sample force F

can be directly calculated with Hooke’s

law: F

= c

·Δz,wherec

denotes the spring constant of the cantilever. In the vari-

ous dynamicmodes, the cantileveris oscillated with amplitude A at or nearits eigen-

frequency f

, but in some applications also oﬀ-resonance. At ambient pressures or

in liquids, amplitude modulation (AM-SFM) is used to detect amplitude changes

or the phase shift between the driving force and cantilever oscillation. In vacuum,

the frequencyshift Δ f of the cantilever due to a tip–sample interaction is measured

by the frequency-modulation technique (FM-SFM). The nomenclature is not stan-

dardized. Terms like tapping mode or intermittent contact mode are used instead of

AM-SFM, and NC-AFM (noncontact atomic force microscopy) or DFM (dynamic

force microscopy) instead of FM-SFM or FM-AFM. However, all these modes are

dynamic, i.e., they involve an oscillating cantilever and can be used in the noncon-

tact, as well as in the contact, regime. Therefore, we believe that the best and most

consistent way is to distinguish them by their diﬀerent detection schemes. Convert-

ing the measured quantity (amplitude, phase, or frequency shift) into a physically

meaningful quantity, e.g., the tip–sample interaction force F

or the force gradient

∂F

/∂z, is not always straightforward and requires an analysis of the equation of

motion of the oscillating tip (see Chaps. 4 and 6).

Whatever method is used, the resolution of a cantilever-based force detection is

fundamentally limited by its intrinsic thermomechanical noise. If the cantilever is

in thermal equilibrium at a temperature T, the equipartition theorem predicts a ther-

mally induced root mean square (rms) motion of the cantilever in the z direction

of z

rms

= (k

T/c

eﬀ

)

1/2

,wherek

is the Boltzmann constant and c

eﬀ

= c

+ ∂F

/∂z.

Note that usually dF

/ dz  c

in the contact mode and dF

/ dz < c

in the non-

contact mode. Evidently, this fundamentally limits the force resolution in the static

mode, particularly if operated in the noncontact mode. Of course, the same is true

for the diﬀerent dynamic modes, because the thermal energy k

T excites the eigen-

frequency f

of the cantilever. Thermal noise is white noise, i.e., its spectral density

is ﬂat. However, if the cantilever transfer function is taken into account, one can see

that the thermal energy mainly excites f

. This explains the term thermo in thermo-

mechanical noise, but what is the mechanical part?

5 Low-Temperature Scanning Probe Microscopy 209

A more detailed analysis reveals that the thermally induced cantilever motion is

given by

rms



πc

, (5.2)

where B is the measurement bandwidth and Q is the quality factor of the can-

tilever. Analogous expressions can be obtained for all quantities measured in dy-

namic modes, because the deﬂection noise translates, e.g., into frequency noise [5].

Note that f

and c

are correlated with each other via 2π f

= (c

eﬀ

)

1/2

,wherethe

eﬀective mass m

eﬀ

depends on the geometry, density, and elasticity of the material.

The Q-factor of the cantilever is related to the external damping of the cantilever

motion in a medium and on the intrinsic damping within the material. This is the

mechanical part of the fundamental cantilever noise.

It is possible to operate a low-temperature force microscope directly immersed

in the cryogen [117,118] or in the cooling gas [119], whereby the cooling is simple

and very eﬀective. However, it is evident from (5.2) that the smallest fundamental

noise is achievable in vacuum, where the Q-factors are more than 100times larger

than in air, and at low temperatures.

The best force resolution up to now, which is better than 1×10

−18

N/Hz

1/2

,has

been achievedby Mamin et al. [120]in vacuumat a temperaturebelow300 mK. Due

to the reduced thermal noise and the lower thermal drift, which results in a higher

stability of the tip–sample gap and a better signal-to-noise ratio, the highest resolu-

tion is possible at low temperatures in ultrahigh vacuum with FM-SFM. A vertical

rms noise below 2 pm [121,122] and a force resolution below 1aN [120] have been

reported.

Besides the reducednoise, the application of force detectionat low temperatures

is motivated by the increased stability and the possibility to observe phenomena that

appear below a certain critical temperature T

, as outlined on page 181. The experi-

ments, which havebeen performedat low temperatures untilnow, were motivatedby

at least one of these reasons and can be roughlydivided into four groups: (i) atomic-

scale imaging, (ii) force spectroscopy, (iii) investigation of quantum phenomena

by measuring electrostatic forces, and (iv) utilizing magnetic probes to study fer-

romagnets, superconductors, and single spins. In the following, we describe some

exemplary results.

5.5.1 Atomic-Scale Imaging

In a simpliﬁed picture, the dimensions of the tip end and its distance to the surface

limit the lateral resolution of force microscopy, since it is a near-ﬁeld technique.

Consequently, atomic resolution requires a stable single atom at the tip apex that

has to be brought within a distance of some tenths of a nanometer to an atomically

ﬂat surface. The latter condition can only be fulﬁlled in the dynamic mode, where

the additional restoring force c

A at the lower turnaround point prevents the jump-

to-contact. As described in Chap. 4, by preventing the so-called jump-to-contact

210 Markus Morgenstern et al.

true atomic resolution is nowadays routinely obtained in vacuum by FM-AFM. The

nature of the short-range tip–sample interaction during imaging with atomic resolu-

tion has been studied experimentallyas well as theoretically. Si(111)-(7×7) was the

ﬁrst surface on which true atomic resolution was achieved[123], and severalstudies

have been performed at low temperatures on this well-known material [124–126].

First-principlessimulations performedon semiconductorswith a silicon tip revealed

that chemical interactions, i.e., a signiﬁcant charge redistribution between the dan-

glingbonds ofthe tip and sample,dominatethe atomic-scale contrast[127–129].On

V–IIIsemiconductors,it was found that onlyone atomic species,the group V atoms,

is imaged as protrusionswith a silicon tip [128,129].Furthermore, these simulations

revealed that the sample, as well as the tip atoms are noticeablydisplaced from their

equilibrium position due to the interaction forces. At low temperatures, both aspects

could be observed with silicon tips on indium arsenide [121,130]. On weakly inter-

acting surfaces the short-range interatomic van der Waals force has been believed

responsible for the atomic-scale contrast [131–133].

Chemical Sensitivity of Force Microscopy

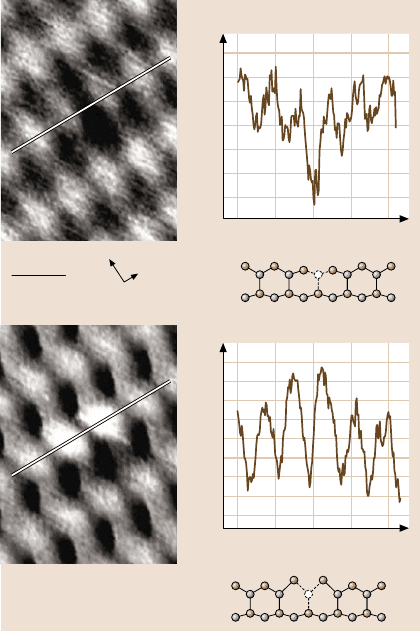
The (110) surface of the III–V semiconductor indium arsenide exhibits both atomic

species in the top layer (see Fig. 5.18a). Therefore, this sample is well suited to

study the chemical sensitivity of force microscopy [121]. In Fig. 5.18b, the usually

observed atomic-scale contrast on InAs(110) is displayed. As predicted, the arsenic

atoms, which are shifted by 80 pm above the indium layer due to the (1 ×1) re-

laxation, are imaged as protrusions. While this general appearance was similar for

most tips, two other distinctively diﬀerent contrasts were also observed: a second

protrusion (c) and a sharp depression (d). The arrangement of these two features

corresponds well to the zigzag conﬁguration of the indium and arsenic atoms along

the [1

10]-direction. A sound explanation would be as follows: the contrast usually

obtained with one feature per surface unit cell corresponds to a silicon-terminated

tip, as predicted by simulations. A diﬀerent atomic species at the tip apex, however,

1 nm

10]

[00

In 1st layer

In 2nd layer

As 1st layer

As 2nd layer

10]

[00

b) c) d)

Fig. 5.18. The structure of InAs(110) as seen from above (a) and three FM-AFM images of

this surface obtained with diﬀerent tips at 14 K (b)–(d). In (b), only the arsenic atoms are im-

aged as protrusions, as predicted for a silicon tip. The two features in (c)and(d) corresponds

to the zigzag arrangement of the indium and arsenic atoms. Since force microscopy is sen-

sitive to short-range chemical forces, the appearance of the indium atoms can be associated

with a chemically diﬀerent tip apex

5 Low-Temperature Scanning Probe Microscopy 211

can result in a very diﬀerent charge redistribution. Since the atomic-scale contrast

is due to a chemical interaction, the two other contrasts would then correspond to

a tip that has been accidentally contaminated with sample material (an arsenic or

indium-terminated tip apex). Nevertheless, this explanation has not yet been veri-

ﬁed by simulations for this material.

Tip-Induced Atomic Relaxation

Schwarz et al. [121] were able to visualize directly the predicted tip-induced relax-

ation during atomic-scale imaging near a point defect. Figure 5.19 shows two FM-

AFM images of the same point defect recorded with diﬀerent constant frequency

shifts on InAs(110), i.e., the tip was closer to the surface in (b) compared to (a).

The arsenic atoms are imaged as protrusions with the silicon tip used. From the

symmetry of the defect, an indium-site defect can be inferred, since the distance-

dependent contrast is consistent with what is expected for an indium vacancy. This

expectation is based on calculations performed for the similar III–V semiconductor

GaP(110), where the two surface gallium atoms around a P-vacancy were found to

z (pm)

10]

direction (nm)

0.0

–5

–10

–15

0.5 1.0 1.5 2.0

z (pm)

10]

direction (nm)

0.0

–10

0.5 1.0 1.5 2.0

1 nm

[001]

10]

Fig. 5.19. Two FM-AFM im-

ages of the identical indium-

site point defect (presumably

an indium vacancy) recorded

at 14 K. If the tip is relatively

far away, the theoretically

predicted inward relaxation

of two arsenic atoms adjacent

to an indium vacancy is visi-

ble (a). At a closer tip–sample

distance (b), the two arsenic

atoms are pulled farther to-

ward the tip compared to the

other arsenic atoms, since

they have only two instead of

three bonds