Bhushan B. Nanotribology and Nanomechanics: An Introduction

Подождите немного. Документ загружается.

1042 B. Bhushan et al.

Pitch ( m)μ

50 100 250

150 200

14 m diameter, 30 m height pillarsμμ

Pitch ( m)μ

180

150

120

50 100 250

Static contact angle (deg)

150 200

Transition criteria range

Droplet with 1 mm Radius

5 m diameter, 10 m height pillarsμμ

Cassie and

Baxter regime

Wenzel

regime

Pitch ( m)μ

180

150

120

50 100 250

Hysteresis and tilt angle (deg)

150 200

Cassie and

Baxter regime

Wenzel

regime

14 m diameter, 30 m height pillarsμμ

Transition criteria range

Droplet with 1 Radiusmm

Pitch ( m)μ

50 100 250

150 200

Tilt angle

Hysteresis

5 m diameter, 10 m height pillarsμμ

Tilt angle

Hysteresis

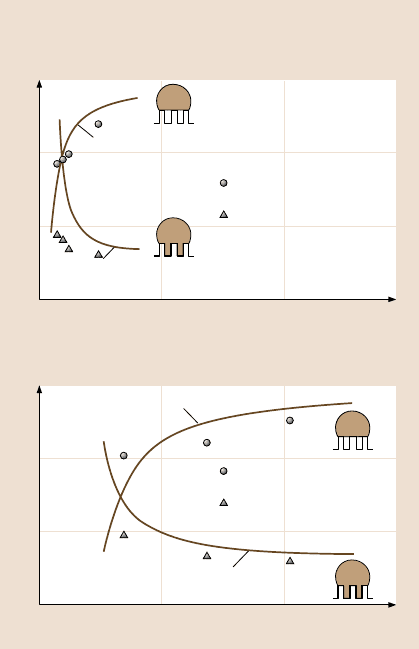
Static contact angle data

Hysteresis and tilt angle data

Static contact angle (deg)

Hysteresis and tilt angle (deg)

Fig. 19.23. (a) Static contact

angle (adotted line represents

the transition criteria range

obtained using (19.25) and

(b) hysteresis and tilt angles

as a function of geometric

parameters for two series of

the patterned surfaces with

diﬀerent pitch values for

adropletwith1mminradius

(5 µL volume). Data at zero

pitch correspond to a ﬂat

sample [18,69]

19 Lotus Eﬀect: Roughness-Induced Superhydrophobic Surfaces 1043

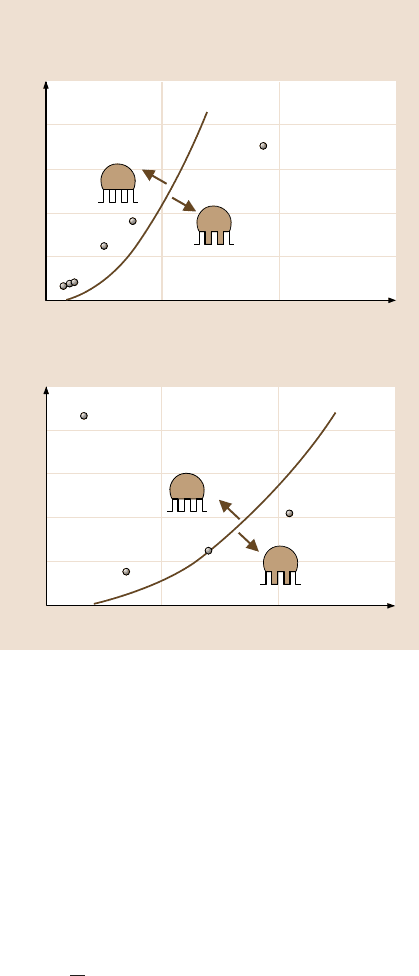
Patterned surfaces with 5 m diameter

and 10 m height pillars

with different pitch values

75 m pitchμ

37.5 m pitchμ

7 m pitchμ

0 m pitchμ

1mm

Fig. 19.24. Optical micrographs of droplets on

the inclined patterned surfaces with diﬀerent pitch

values. The images were taken when the droplet

started to move down. Data at zero pitch corre-

spond to a ﬂat sample [18]

1044 B. Bhushan et al.

on the patterned Si with 45µm of series 1 and 126µm of series 2. As discussed

earlier, an increase in the pitch value allows the formation of composite interface.

At higher pitch values, it is diﬃcult to form the composite interface. The decrease

in hysteresis and tilt angles occurs due to formation of composite interface at pitch

values raging from 7µmto45µm in series 1 and from 21µm to 126 µminseries2.

The hysteresis and tilt angles start to increase again due to lack of formation of air

pockets at pitch values raging from 60 µmto75µm in series 1 and from 168 µm

to 210 µm in series 2. These results suggest that the air pocket formation and the

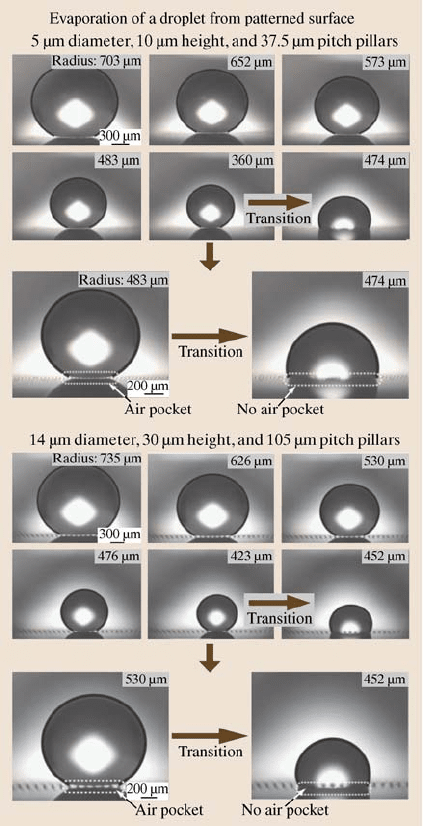
Fig. 19.25. Evaporation of

a droplet on two diﬀerent

patterned surfaces. The initial

radius of the droplet is about

700 µm, and the time interval

between successive photos is

30 s. As the radius of droplet

reaches 360 µmonthesur-

face with 5 µm diameter,

10 µm height, and 37.5 µm

pitch pillars, and 420 µmon

the surface with 14 µmdi-

ameter, 30 µm height, and

105 µm pitch pillars, the tran-

sition from the Cassie–Baxter

regime to Wenzel regime

occurs, as indicated by the ar-

row. Before the transition, air

pocket is clearly visible at the

bottom area of the droplet, but

after the transition, air pocket

is not found at the bottom

area of the droplet [69]

19 Lotus Eﬀect: Roughness-Induced Superhydrophobic Surfaces 1045

reduction of pinning in the patterned surface play an important role for a surface

with both low hysteresis and tilt angle [18,19]. Hence, to create superhydrophobic

surfaces, it is important that they are able to form a stable composite interface with

air pockets between solid and liquid. Capillary waves, nanodroplet condensation,

hydrophilic spots due to chemical surface inhomogeneity, and liquid pressure can

destroy the composite interface. Nosonovsky and Bhushan [100,101,103–106] sug-

gested that these factors which make the composite interface unstable have diﬀerent

characteristic length scales, so nanostructures or the combination of microstructures

and nanostructures is required to resist them.

Observation of Transition During the Droplet Evaporation

Jung and Bhushan [68, 69] performed the droplet evaporation experiments to ob-

serve the Cassie–Wenzel transition on two diﬀerent patterned Si surfaces coated

with PF

. The series of six images in Fig. 19.25 show the successive photos of

a droplet evaporating on the two patterned surfaces. The initial radius of the droplet

was about 700µm, and the time interval between successive photos was 30s. In the

ﬁrst ﬁve photos, the droplet is shown in a Cassie–Baxter state, and its size gradually

decreases with time. However, as the radius of the droplet reached 360µmonthe

surface with 5µm diameter, 10µm height, and 37.5µm pitch pillars, and 423µmon

the surface with 14µm diameter, 30µm height, and 105µm pitch pillars, the transi-

tion from the Cassie–Baxter to Wenzel regime occurred, as indicated by the arrow.

Figure 19.25 also shows a zoom-in of water droplets on two diﬀerent patterned Si

surfaces coated with PF

before and after the transition. The light passes below the

left droplet, indicating that air pockets exist, so that the droplet is in the Cassie–

Baxter state. However, an air pocket is not visible below the bottom right droplet,

so it is in the Wenzel state. This could result from an impalement of the droplet in

the patterned surface, characterized by a smaller contact angle.

To ﬁnd the contact angle before and after the transition, the values of the con-

tact angle are plotted against the theoretically predicted value, based on the Wenzel

(calculated using (19.6)) and Cassie–Baxter (calculated using (19.9)) models. Fig-

ure 19.26 shows the static contact angle as a function of geometric parameters for

the experimental contact angles before (circle) and after (triangle) the transition

compared with the Wenzel and Cassie–Baxter equations (solid lines) with a given

value of θ

for two series of the patterned Si with diﬀerent pitch values coated with

[69]. The ﬁt is good between the experimental data and the theoretically pre-

dicted values for the contact angles before and after transition.

To prove the validity of the transition criteria in terms of droplet size, the critical

radiusof dropletdepositedon thepatternedSi withdiﬀerent pitch valuescoatedwith

is measured during the evaporation experiment [68, 69]. Figure 19.27 shows

the radius of a droplet as a function of geometric parameters for the experimental

results (circle) compared with the transition criterion (19.5) from the Cassie–Baxter

regime to Wenzel regime (solid lines) for twoseries of the patterned Si with diﬀerent

pitch values coated with PF

. It is found that the critical radius of impalement is in

good quantitative agreement with our predictions. The critical radius of the droplet

1046 B. Bhushan et al.

Pitch ( m)μ

Contact angles before and after transition

14 m diameter, 30 m height pillarsμμ

5 m diameter, 10 m height pillarsμμ

180

150

120

50 100 150

Wenzel’s equation

Cassie and Baxter’s equation

180

150

120

50 100 150

Wenzel’s equation

Cassie and Baxter’s equation

Static contact angle (deg)

Receding contact angle

before transition

Receding contact angle

after transition

Receding contact angle

before transition

Receding contact angle

after transition

Fig. 19.26. Receding contact

angle as a function of geomet-

ric parameters before (circle)

and after (triangle) transi-

tion compared with predicted

static contact angle values

obtained using the Wenzel

and Cassie–Baxter equations

(solid lines) with a given

value of θ

for two series of

the patterned surfaces with

diﬀerent pitch values [69]

increases linearly with the geometric parameter (pitch). For the surface with small

pitch, the critical radius of droplet can become quite small.

To verify the transition, Jung and Bhushan [68,69] used another approach using

the dust mixed in water. Figure 19.28 presents the dust trace remaining after droplet

with 1mm radius (5 µL volume) evaporation on the patterned Si surface with pillars

of 5µm diameter and 10µm height with 37.5 µm pitch in which the transition oc-

curred at 360µm radius of the droplet, and with 7µm pitch in which the transition

occurred at about 20µm radius of the droplet during the process of evaporation. As

shown in the top image, after the transition from the Cassie–Baxter regime to Wen-

zel regime, the dust particles remained not only at the top of the pillars but also at

the bottom with a footprint size of about 450 µm. However, as shown in the bottom

image, the dust particles remained on only a few pillars until the end of the evap-

oration process. The transition occurred at about 20µm radius of droplet and the

dust particles left a footprintof about25 µm. From Fig. 19.27, it is observed that the

transition occurs at about 300µm radius of droplet on the 5 µm diameter and 10µm

height pillars with 37.5µm pitch, but the transition does not occur on the patterned

19 Lotus Eﬀect: Roughness-Induced Superhydrophobic Surfaces 1047

Pitch ( m)μ

Transition from Cassie-Baxter regime to Wenzel regime

14 m diameter, 30 m height pillarsμμ

5 m diameter, 10 m height pillarsμμ

1000

800

50 100 150

1000

800

600

400

200

50 100 150

Radius of droplet ( )mμ

Wenzel

regime

Cassie and

Baxter regime

Exper. transition

600

400

200

Cassie and

Baxter regime

Exper. transition

Radius of droplet ( )mμ

Wenzel

regime

Fig. 19.27. Radius of droplet

as a function of geometric

parameters for the experi-

mental results (circle)com-

pared with the transition cri-

teria from the Cassie–Baxter

regime to Wenzel regime

(solid lines) for two series of

the patterned surfaces with

diﬀerent pitch values [69]

Si surface with pitch of less than about 5 µm. These experimental observations are

consistent with model predictions. In the literature, it has been shown that on super-

hydrophobic natural lotus, the droplet remains in the Cassie–Baxter regime during

the evaporation process [142]. This indicates that the distance between the pillars

should be minimized enough to improve the ability of the droplet to resist sinking.

Scaling of the Cassie-Wenzel Transition for Diﬀerent Series

Nosonovsky and Bhushan [101–104, 106] studied the data for the Cassie–Wenzel

transition with the two series of the surfaces using the non-dimensional spacing

factor

. (19.26)

The values of the droplet radius at which the transition occurs during the evapo-

ration plotted against the spacing factor scale well for the two series of the experi-

mental results, yielding virtually the same straight line. Thus the two series of the

1048 B. Bhushan et al.

100 mμ

Dust trace after droplet evaporation

5 m diameter, 10 m height, and 7 m pitch pillarsμμ μ

5 m diameter, 10 m height, and 37.5 m pitch pillarsμμ μ

10 mμ

Fig. 19.28. Dust trace re-

mained after droplet evapora-

tion for the patterned surface.

In the top image, the tran-

sition occurred at 360 µm

radius of droplet, and in the

bottom image, the transition

occurred at about 20 µmra-

dius of droplet during the

process of droplet evapora-

tion. The footprint size is

about 450 and 25 µmforthe

top and bottom images, re-

spectively [69]

patterned surfaces scale well with each other and the transition occurs at the same

value of the spacing factor multiplied by the droplet radius (Fig. 19.29). The phys-

ical mechanism leading to this observation remains to be determined, however, it

is noted that this mechanism is diﬀerent from the one suggested by 19.25. The ob-

servation suggests that the transition is a linear “1D” phenomenon and that neither

droplet droop (that would involve P

/H) nor droplet weight (that would involve

) are responsible for the transition, but rather linear geometric relations are in-

volved. Note that the experimental values approximately correspond to the values

of the ratio RD/P = 50µm, or the total area of the pillar tops under the droplet

(πD

/4)πR

= 6200µm

19 Lotus Eﬀect: Roughness-Induced Superhydrophobic Surfaces 1049

500

100

2648

200

300

400

b) Droplet radius, R (m)μ

Spacing factor, S

1.0

0.8

0.6

0.4

0.2

0.1 0.3 0.5

a) cos – cosθθ

rec adv

0.2 0.4

1/s

Wenzel

Cassie

c = 0.5

c = 0

Cassie

Wenzel

Fig. 19.29. (a) contact angle hysteresis as a function of S

for the 1st (squares) and 2nd

(diamonds) series of the experiments compared with the theoretically predicted values of

cosθ

adv

−cosθ

rec

= (D/P)

(π/4)(cosθ

adv0

−cosθ

rec0

)+ c(D/P)

,wherec is a proportional-

ity constant. It is observed that when only the adhesion hysteresis/interface energy term is

considered (c = 0), the theoretical values are underestimated by about a half, whereas c = 0.5

provides a good ﬁt. Therefore, the contribution of the adhesion hysteresis is of the same

order of magnitude as the contribution kinetic eﬀects. (b) Droplet radius, R, for the Cassie–

Wenzel transition as a function of P/D = 1/S

. It is observed that the transition takes place

at a constant value of RD/P ∼ 50 µm(dashed line). This shows that the transition is a linear

phenomenon

Contact Angle Hysteresis and Wetting/Dewetting Asymmetry

The contactangle hysteresiscan be viewed as a result oftwo factorsthat act simulta-

neously. First, the changing contact area aﬀects the hysteresis, since a certain value

ofthe contact anglehysteresisis inherentfor evennominallyﬂat surface.Decreasing

the contact area by increasing the pitch between the pillars leads to a proportional

decrease of the hysteresis. This eﬀect is clearly proportional to the contact area

between the solid surface and the liquid droplet. Second, edges of the pillar tops

1050 B. Bhushan et al.

prevent the motion of the triple line. This roughness eﬀect is proportional to the

contact line density and its contribution was, in the experiment, comparable with

the contact area eﬀect. Interestingly, the eﬀect of the edges is much more signiﬁcant

for the advancing than for the receding contact angle.

Nosonovsky and Bhushan [101–104,106] studied wetting of two series of pat-

terned Si surfaces with diﬀerent pitch values coated with PF

based on the spacing

factor (19.26). They found that the contact angle hysteresis involves two terms: the

term S

(π/4)(cosθ

adv0

−cosθ

rec0

) corresponding to the adhesion hysteresis (which

is found even at a nominally ﬂat surface and is a result of molecular-scale imper-

fectness) and the term H

∝ D/P

corresponding to microscale roughness and pro-

portional to the edge line density. Thus the contact angle hysteresis is given, based

on (19.19), by [16,100]

cosθ

adv

−cosθ

rec

(

cosθ

adv0

−cosθ

rec0

)

+ H

. (19.27)

Besides the contact angle hysteresis, the asymmetry of the Wenzel and Cassie states

is the result of the wetting/dewetting asymmetry. While fragile metastable Cassie

state is often observed, as well as its transition to the Wenzel state, the opposite

transition never happens. Using (19.6) and (19.9) the contact angle with the pat-

terned surfaces is given by [16,100]

cosθ =



1+ 2πS



cosθ

(Wenzel state) (19.28)

cosθ =

(cosθ

+ 1)−1 (Cassie state) . (19.29)

For a perfect macroscale system, the transition between the Wenzel and Cassie

states should occur only at the intersection of the two regimes (the point at which

the contact angle and net energies of the two regimes are equal, corresponding to

= 0.51). It is observed, however, that the transition from the metastable Cassie to

stable Wenzel occurs at much lower values of the spacing factor 0.083< S

< 0.111.

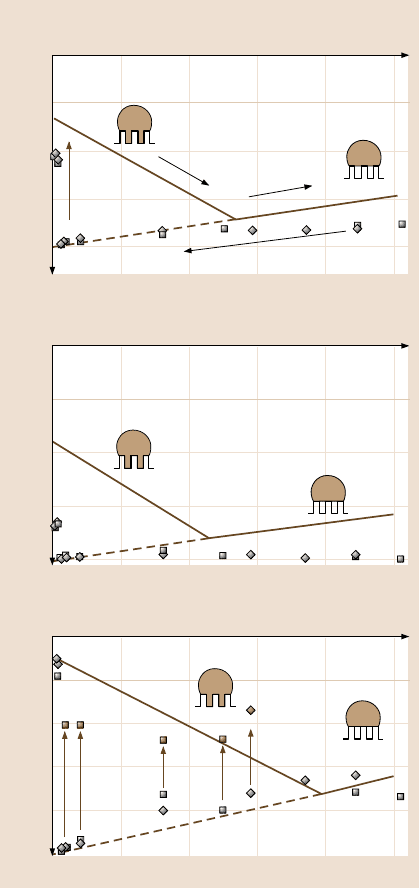
As shown in Fig. 19.30a, the stable Wenzel state (i) can transform into the stable

Cassie state with increasing S

(ii). The metastable Cassie state (iii) can abruptly

transform (iv) into the stable Wenzel state. The transition (i–ii) correspondsto equal

Wenzel and Cassie states free energies, whereas the transition (iv) corresponds to

the Wenzel energy much lower than the Cassie energy and thus involves signiﬁcant

energydissipationand is irreversible.The solid and dashed straightlines correspond

to the values of the contact angle, calculated from (19.28)–(19.29)using the contact

angle for a nominally ﬂat surface, θ

= 109

◦

. The two series of the experimentaldata

are shown with squares and diamonds.

Figure 19.30b shows the values of the advancing contact angle plotted against

the spacing factor (19.26). The solid and dashed straight lines correspond to the val-

ues of the contact angle for the Wenzel and Cassie states, calculated from (19.28)–

(19.29) using the advancing contact angle for a nominally ﬂat surface, θ

adv0

= 116

◦

It is observed that the calculated values underestimate the advancing contact angle,

especially for big S

(small distance between the pillars or pitch P). This is under-

standable, because the calculation takes into account only the eﬀect of the contact

19 Lotus Eﬀect: Roughness-Induced Superhydrophobic Surfaces 1051

Metastable Cassie

Spacing factor, S

–0.25

0.1

0.2 0.5

Wenzel

cosθ

–0.50

–0.75

–1.00

0.25

0.3 0.4

Cassie

Metastable Cassie

Spacing factor, S

–0.25

0.1

0.2 0.5

cosθ

–0.50

–0.75

–1.00

0.3 0.4

Metastable Cassie

Spacing factor, S

–0.25

0.1

0.2 0.5

cosθ

–0.50

–0.75

–1.00

0.3 0.4

Cassie

Wenzel

Cassie

Wenzel

iii

Fig. 19.30. Theoretical (solid

and dashed) and experimen-

tal (squares for the 1st series,

diamonds for the 2nd series)

(a) contact angle as a func-

tion of the spacing factor. (b)

Advancing contact angle (c)

Receding contact angle and

values of the contact angle

observed after the transition

during evaporation (blue)

area and ignores the eﬀect of roughness and edge line density (it corresponds to

= 0 in (19.27)), while this eﬀect is more pronounced for high pillar density (big

). In a similar manner, the contact angle is underestimated for the Wenzel state,

since the pillars constitute a barrier for the advancing droplet.

Figure 19.30c shows the values of the contact angle after the transition took

place (dimmed blue squares and diamonds), as it was observed during evaporation.